Double Pendulum '4d-Var' Demonstration Package
Double Pendulum '4d-Var' Demonstration Package
Ross Bannister, Data Assimilation Research Centre, University of Reading, UKLast updated 28th January 2002
What is 4d-Var used for?
Four dimensional variational data assimilation (or 4d-Var) is a means of estimating the initial conditions of a model by optimizing the fit between real observations and predicted 'observations' found from a projection of the model forward in time. The four dimensions are comprised of three spatial and one time. You can find out more about 4d-Var in the DARC technical report #2 in html or postscript formats.
Data assimilation is used to initialize models that forecast the weather, making use of a wide range of recent measurements of the global weather. This enables forecasters to launch weather prediction models, starting from a realistic state representative of the current weather conditions.
Our "4d Var" demonstration package
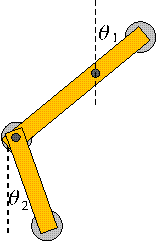
The double pendulum system
|
Numerical weather prediction models are complicated, cumbersome, and require extensive resources to work. To demonstrate the technique of 4d-Var, we resort to a very simple physical system that has itself little to do with atmospheric science - the double pendulum. Unlike a weather prediction model, which could contain over a million degrees of freedom, the double pendulum is described by just four variables. These the are two angles (see Fig.) and their time rates of changes. These are also explained in separate gzipped postscript documents 1 and 2, as is how the double pendulum model is integrated in time. |
The equations of motion are comprised of coupled ordinary differential equations, rather than of partial differential equations as an atmospheric model is. We cannot therefore speak of a number of spatial dimensions in the same way that we can with an atmospheric model. The term "4d-Var" is somewhat a misnomer, but the distinguishing thing about 4d-Var is that there is a time dimension - which we have. We should more aptly call the weather forecasting "4d-Var" technique "3+1d-Var", and perhaps for the double pendulum system, "1+1d-Var".
Assimilation cycles
Intermittent data assimilation (as we are doing here) is performed in cycles. Each cycle spans a time interval, within which all observations are analysed, and merged with the model. The objective of this procedure is to estimate of the optimal initial conditions (relevant to the start of the cycle) which will reproduce, via the model, the observations. The idea is that the integration can then be advanced further to forecast future states of the system.
A guide to using the double pendulum "4d-Var" code
Downloading and compiling the appropriate files
Download the following files onto your own system (click on each of them in turn and use your browser to download):
- Assim.f This is the complete Fortran 77 source code. No special libraries are required.
- Assim.conf This is an example configuration file for the code. When running, the program will read information from this file. It can be edited using a text editor and such information can be entered like:
- the run mode,
- the number of observations,
- the model parameters,
- the length of the assimilation cycles,
- the observations themselves,
- etc.
You will have to compile the source code yourself and so you will need a Fortran 77 (or Fortran 90) compiler. For suitably equipped UNIX systems, the compilation is achieved by something like,
f77 Assim.f -o Assim.out
which names the executable as "Assim.out".
Run modes - "MakeObs", "Analyse" and "Insert"
There are three run modes that the code will run under (you specify the run mode in the configuration file "Assim.conf"). The first is called "MakeObs". We have no actual observations, and so this mode allows us to generate synthetic observations. This is done by adding noise to a simple model run. The second mode, "Analyse", assimilates these pseudo observations into the model using "4d-Var" to perform the optimization process. The last mode, "Insert", is a crude assimilation scheme that simply inserts the actual observations into the integration as it progresses. Inserting observations like this does not give dynamically consistent prognosis and so this kind of 'assimilation' is expected to give bad analyses and forecasts and is included for the purposes of comparison with the variational method.
The configuration file "Assim.conf"
The configuration file will look something like the following:
========================================================================
4dVar (Double Pendulum) Input File
========================================================================
====== General Parameters ==============================================
--Status ('MakeObs'=invent obs, 'Analyse'=4dVar, 'Insert'=simple insrt.)
MakeObs
--Dimensions of pendulum (l1,l2,l3, metres)
0.1, 0.2, 0.15
--Masses of pendulum nodes (m1,m2,m3, kg)
0.1, 0.1, 0.1
--Acceleration due to gravity (m/s/s)
10.0
--Time step (seconds)
0.001
--Length of integration (time steps)
5000
--Model state (initial guess(Analyse) or initial conditions(MakeObs))
--angle 1,angle 2, roc angle 1, roc angle 2 (deg and deg/s)
160.0, 100.0, -350.0, 100.0
========================================================================
====== MakeObs Parameters ==============================================
--Frequency of observation output (used only for MakeObs)
50
--Noise for angles (deg, used only for MakeObs)
5.0
--Noise for roc angles (deg/s used only for MakeObs)
0.0
========================================================================
====== Analyse/Insert Parameters =======================================
--Size of each observation window (time steps)
500
--Observations (used only for Analyse)
--Value, type (1,2,3,4), error, time (sec)
------------------------------------------------------------------------
000.00, 0, 000.00, 000.00
------------------------------------------------------------------------
========================================================================
There are three sections. The first section "General Parameters" allows us to specify the run mode, the model parameters (see notes referred to above) and the length and number of assimilation cycles. The second "MakeObs Parameters" relates to the generation of the pseudo observations, and the final section "Analyse/Insert Parameters" pertains to the assimilation process, and when used, will contain the list of pseudo observations. More info below.
** Choosing the system parameters and generating observations **
We now take you through the ten lines of information that needs to be specified to generate pseudo obs.
1. Status (for run mode)
Make sure that the run mode is set to "MakeObs" (as in the example file above).
2. Dimensions of pendulum
Specify the physical parameters that describe the double pendulum (see notes). The parameters are comprised of three lengths ...
3. Masses
...and three masses.
4. Acceleration due to gravity
The acceleration due to gravity is set to an Earth-like value in the above example, but can be changed.
5. Time step
This is the integration time step.
6. Length of integration
This describes the total length in time of the experiment and is an integer number of integration time steps.
7. Initial model state
The prognostic variables consist of two angles and two angular speeds. Such a starting state of the model for this run should be specified here. The projection of these variables in time is regarded as the exact solution, and serves two purposes. It firstly allows us to invent observations (by adding random noise - see below) and provides us with the 'true solution' to validate our assimilation against.
The next three parameters are used only when generating pseudo observations.
8. Frequency of observation output
Since the number of integration steps (6. above) is usually large, we may not wish to have as many pseudo observations. The number specified in this field gives the interval (in integration steps) between output of observations. This make the assimilation process (see below) a 'realistic' test of the technique as in weather forecasting, observations are made generally less frequently than the model time step.
9. Noise for angles
This is akin to the variance of the random noise added to the angular prognostic variables.
10. Noise for roc angles
This is akin to the variance of the random noise added to the angular-speed prognostic variables (roc = "rate of change"). The assimilation does not always need speed observations to converge. Setting the noise to "0.0" instructs the program to omit outputting these kinds of observations.
The output from the program when run in "MakeObs" mode is comprised of two files:
"Observations"
This file contains the observations - one per line. Each line has the following format:
value of prognostic variable, variable type, error, time
The units of the prognostic variables and errors in this file are in radians (or radians/second, depending upon the variable), even though degrees are used in the configuration file. The variable type has the following key: 1=angle 1, 2=angle 2, 3=roc angle 1, 4=roc angle 2 (where "roc"="rate of change"). The errors (uncertainty of the measurements) is copied from the configuration file (9. or 10. above), but, as already mentioned, converted into radians or radians/second. The time that each observation is 'made' is the last element.
The last line should always consist of an end-of-file marker (four zeros).
This file is used in the assimilation, and should be 'pasted' into a new configuration file for the assimilation run (details below). The analysis software has been designed to allow the user to edit the observations at will. E.g., we may wish to remove one or more observations (or even 'wipe-out' all in a significant time window), investigate the effect of adding anomalous observations, or making the associated error values too small or large.
"Assim.ObsBase"
This file contains the true solution. Output is produced every timestep according to the following format:
time, angle 1, angle 2, roc angle 1, roc angle 2
(as with the "Observations" file, the units are radians for the two angles, and radians/second for the angular speeds). When performed, the assimilation run (see below) will try to recover this solution purely from the noisy observations.
** Performing the variational assimilation **
The configuration file is set up a different way to run the software in one of the assimilation modes. To do variational data assimilation, first change the status from "RunMode" to "Analyse". Make sure, also that the observations (from the "Observations" above) have been pasted into the bottom section of the file, just before the row of zeros. Edit them as required - there can be as many or as few observation lines as you like. The meaning of each element of the line is the same as the format of the "Observations" file detailed above.
There are a few other items to change in the configuration file. The duration of each assimilation cycle must be specified (in time steps). In principle this can be any positive integer, but should be set, usually, to a value less than the total length of the integration (item 6 above). The run will then consist of more than one assimilation cycle. Note that there does not have to be a whole number of cycles in the complete run - if the length of the integration is not a multiple of the cycle length, then the last cycle will be slightly shorter than the previous ones. In order to gauge a value of this parameter that will give good results, plot, say, angle 1, as a function of time (using the file "Assim.ObsBase" from the MakeObs run) and find out how many time steps correspond to one pseudo-period of the system.
Finally, a guess of the initial conditions must be specified (write over line 7 above). Of course, in a real run we would not know what these values are, and it is the job of the assimilation scheme to estimate them. The scheme does need an 'educated guess' to start with, which often would be known in a practical application. Choose values which are not too far from the exact initial conditions used for the observations run.
The other "general parameters" such as the physical characteristics of the system, etc., should not be changed. The scheme is written in the strong constraint formalism and so we are assuming that the model is perfect. This implies that the physical parameters must be correct and so be unchanged. The length of the integration can, however, be modified if required (e.g. increase it to include a 'forecast' part of the run).
The output files from the assimilation
There are many files output from the assimilation. The units used for the various quantities are seconds, radians and radians/second.
"Assim.anal"
This file is comprised of the timestep-by-timestep output of integrations of each assimilation cycle. Each integration is initialized from the 'optimal' initial conditions found by the assimilation scheme. The complete file is the analysed output. Each line has the following format:
time, angle 1, angle 2, roc angle 1, roc angle 2
"Assim.obsX"
These files (X=1,2,3,4) contain the observations as contained in the configuration file. The variable type, X, has the following key: 1=angle 1, 2=angle 2, 3=roc angle 1, 3=roc angle 2. Each line has the following format:
time, value of observation, error of observation
Having the observations in separate files like this is convenient for visualization via plotting packages.
"Assim.bnds"
This file specified the times bounding the assimilation cycles (for information).
"Assim.fore"
This is the run starting from the guess state, making use of no observations. This can be compared to the analysed run, "Assim.anal" (it has the same format), to see directly how the information contained in the observations has benefited the assimilation.
"Assim.init"
This file contains the model's analysed initial conditions for each assimilation cycle. In variational data assimilation on this scale we can also compute the uncertainties in the analysed quantities. The uncertainties are a combination of the background and observation errors. The uncertainties are output with the initial conditions and, for a particular cycle, are listed immediately below the initial conditions themselves.
"CyXXLpYY"
There are many files with a name of this structure. These files contain the forecast over assimilation cycle "XX" pertaining to the "YY"th 'guess' of the initial conditions. By plotting out the value of a particular system variable (say angle 1) with time for a particular cycle XX, one should see progressive curves (one for each YY) converge to the evolution of the 'true' system over that time window. These files are provided for diagnostic purposes.
Other information
Other diagnostic information - such as the cost function for each variational iteration of each assimilation cycle (also resolved into its 'background' and 'observation' components) - is output to the standard output. The standard output is usually the screen, but some operating systems will allow it to be redirected to a file for later inspection. E.g. in UNIX,
Assim.out > Assim.diag
will redirect the diagnostic information output by the executable "Assim.out" to the file "Assim.diag".
Performing the assimilation using simple insertion
This is an inferior method of assimilating the observations. In this mode, an integration of the double pendulum is made starting from the initial conditions specified in the "Assim.conf" file. At each stage of the integration when there is an observation, its value simply overwrites the model value at that time. Unlike the variational assimilation run, no account is taken of the observation errors and the prognosis will not be dynamically consistent. To run in this mode, change the run mode (line 1 in the "Assim.conf" file) to "Insert". The remaining parameters to change are the same as for the "Analyse" run detailed above.
The output files from the insertion run
There are a few files output from this insertion run. As before, the units used for the various quantities are seconds, radians and radians/second.
"Assim.ins"
This file is comprised of the timestep-by-timestep output of the integration with each observation inserted. Each line has the following format:
time, angle 1, angle 2, roc angle 1, roc angle 2
"Assim.obsX"
These files (X=1,2,3,4) are described above.
The variational assimilation algorithm
Click here to see the algorithm.
Sample runs of the code
As examples, some runs of the code have been made.
Click here.
Notes for use
The software contained on this site may be used for education and private study purposes only. Please let me know if you have used the code or if you would like to report bugs. The code is owned by Ross Bannister.