CUNDA: Causality Relations using nonlinear Data Assimilation
Scientists
- Prof Manual Pulido: Nonlinear data assimilation and machiine learning
- Prof Magdalena Lucini: Estimation of model error covariances for nonlinear data assimilation
- Dr. Polly Smith: Nonlinear data assimilation
- Dr. Vincent Faure: Physical Oceanography observations
- Dr. Vladimir Stepanov: Physical Ocean modelling
- MSc Matthew Ng: Causality
- Dr. Maria Broadbridge: Scientific programmer
- Prof Peter Jan van Leeuwen: project coordination, nonlinear data asimilation, causality
Under construction !!!
Introduction
The ocean and the atmosphere are high-dimensional turbulent stratified thermodynamic systems that are very difficult to understand. Even if our models would be close to perfect, so we would be able to simulate the real world quite accurately, our understanding of the interactions in the system will be limited. Specifically, there is great interest in which processes are drivers and which processes are more acting like slaves, so in causal relations. Through physical reasoning and order of magnitude estimates we have knowledge of some of the larger-scale linear balances, and we have a rather mature understanding of certain climate modes like El Nino. However, knowledge on nonlinear causal interactions among many scales is largely missing.
An example at the heart of this proposal is the connection between the highly turbulent eddying motion south of the African continent and the interocean exchange between the Indian, the South Atlantic and the Southern Ocean. Warm and salty water from the Indian Ocean is transported to the relatively cold and fresh Atlantic through the shedding of large eddies from the Agulhas Current, called Agulhas Rings. This shedding is a highly irregular turbulent process. It facilitates the global transport of heat and salt in the world oceans, know as the thermohaline circulation, which is a crucial ingredient of the climate system (e.g. De Ruijter et al, 1999). For instance, the relatively mild climate in western Europe compared to eastern North America is directly related to the GulfStream extension that brings warm and salty water from the tropical Atlantic northward into the polar ocean. Via the interocean transport the ocean area around the southern tip of Africa plays a crucial role in this global circulation.
Despite decades of active research it is still unclear what sets this interocean exchange, the local turbulent dynamics, or the global scale dynamics. What has been revealed is that the processes that potentially influence the shedding process are quite diverse (see figure 1), from instabilities in the Agulhas Current (Van Leeuwen et al,2000) , dipoles from the separating East Madagascar Current (Schouten et al, 2002a a,b, Ridderinkhof, 2013), signals from the tropical waters and the Indonesian ThroughFlow (Le Bars et al, 2013), local instabilities of the strong recirculation cell southeast of the continent, direct interactions with the Antarctic Circumpolar Current (ACC), eddies shed from the ACC (Le Bars et al, 2012), and connections between the local dynamics and the weaker recirculation cell southeast of Madagascar. Furthermore, it has been speculated that the zonal density gradient from Indian to Atlantic Ocean plays a large role via the relative vorticity changes enforced on the Agulhas Current through this density gradient, and even larger scale modes of the Southern Ocean Supergyre that connects all subtropical gyres in the southern ocean could play a major role (see figure 1). Unraveling causal relations in this area is a real challenge and can only be achieved with the most sophisticated tools available.
A simple way to quantify these causal interactions is to look at linear correlations, with the underlying hypothesis
that if two processes have a high correlation coefficient they have strong interaction, and if the correlation
coefficient is low the interaction is negligible. Regression analysis is based on this simple idea.
However, it is well realised that this hypothesis can be quite off the mark. If
two processes are nonlinearly correlated, e.g. the correlation is strong along a circle instead of a line,
the correlation coefficient can be close to zero, while the interaction is large.
Nonlinear causality measures do exist. They are based on the reduction of our uncertainty about the
state of a process if we know the state and history of another process.
This uncertainty can be measured by a probability density function, that tells us the probability
of each possible state or evolution of the system.
We will denote the probability density function as pdf from now on.
The narrower the pdf, the more certain we are of what the actual system is doing.
The 'narrowness' of a pdf of arbitrary shape is measured by the entropy of the pdf.
Entropy measures the amount of possible configurations a system can be in, and clearly a
narrow pdf is much more confined, and its entropy will be low.
Causal relations have to do with how the entropy of process $x$ is reduced by knowledge of
the history of another process $y$. So we are looking at the difference between the entropy of process $x$
minus the entropy of process $x$ given the history of process $y$. Clearly, if process $y$ tells us
nothing about process $x$ this difference is zero. If, however, process $y$ does contain information on
process $x$ the entropy of process $x$ is reduced by knowledge of the history of process $y$.
This is the basis of most causality measures that will be discussed next in detail.
Considering the present status of the field, seven problems can by identified:
a) I find that my causality measure (e.g. Transfer Entropy) stands out from the noise.
b) So my result is likely to be caused by the presence of a causal relation.
c) It is therefore likely that I am seeing a causal relation.
d) The result is therefore positive evidence that there is a causal relation.
While this looks ok, it is not, related to a similar mistake often made in hypothesis testing.
The issues is that b) tells us about the probability of the value of causality measure given a certain causality strength
in nature. However, c) informs about the probability of a certain causality strength given the value of the causality
measure. These two are not the same. We are indeed interested in c), but actually calculate b).
Problems 1-4 and 7 need to be solved within information theory, and we will explore a new Bayesian formulation
of the problem to try to solve them, and develop a new method to explore model equations in
causality strength calculations for problem 4, as detailed in section b.
Problems 5 and 6, that observations are incomplete and models is not reality, needs a another solution.
To make the model resemble the true evolution of the system we have to bring in
observations of that system. More specifically, we need to combine the model with these
observations in a systematic way that will not destroy the information flows, but
makes them more accurate. This leads automatically to the use of fully nonlinear data assimilation.
1) staying close to the evolution of the real world, and
2) because of the observational constraints the pdf will be relatively narrow, so a more efficient representation
of the pdf is possible with less computational resources.
Any model simulation will only be an approximation to the real world. Also, each observation of the real world is only an approximation because observation errors are always present.
The uncertainty in the model can be described by a probability density function (pdf).
Observation uncertainty is also described by a pdf, and data assimilation combines these two pdf's.
Bayes Theorem tells us that the updated pdf of the model can be found by multiplying the model pdf with the observations pdf
(or rather the likelihood of the observations given each model state).
The difficulty in nonlinear data assimilation is that the pdf's can have any shape, and the dimension of the space in which the pdf lives is equal to the model dimension. For numerical weather prediction and for the ocean example we will explore here this space can be billion dimensional. Clearly we cannot even store the pdf on the largest computer on Earth, let alone calculate its evolution over time. So, approximations have to be made.
Current data-assimilation methods for high-dimensional systems are all based on linearisations.
For instance, the Kalman Filter assumes that both the model and the observations are Gaussian distributed,
so implicitly all relations between the variables are assumed to be linear. In the
Ensemble Kalman Filter and its Smoother variant (Evensen, 1994, Burgers, Van Leeuwen and Evensen, 1998, Van Leeuwen, 1999, 2001; Evensen and Van Leeuwen, 2000) the evolution of the system is fully nonlinear, but as soon as observations are encountered
the relations between variables is again assumed to be linear.
Variational methods like 4DVAR and its dual (Courtier, 1997) find the mode of the posterior pdf. As they do not provide information on the pdf as a whole they are not of interest here directly, although they can be used in ensemble mode, as discussed later. Also so-called hybrid methods that combine variational and ensemble Kalman filters (see e.g. Zhang et al, 2009) do not solve the linearity issues.
Fully nonlinear data-assimilation methods do exist, but they tend to be inefficient in high-dimensional systems
(see e.g. the review Van Leeuwen, 2009).
Most promising seem to be the so-called Particle Filters (Gordon et al, 1992). As in the Ensemble Kalman Filter the pdf is represented by an ensemble of model states, but without the Gaussian/linearity assumption.
Snyder et al. (2008) proved that under apparently reasonable assumptions Particle Filters are extremely inefficient in high-dimensional systems: the number of model states needed growths exponentially with the dimension of the system.
However, recent progress on particle filtering pioneered by the PI has now lifted this 'curse of dimensionality'.
This proposal will do this by first defining a new quantity called causality strength
to be able to unify different approaches, by employing a Bayesian framework, and by using nonlinear data assimilation.
This leads to the following specific objectives:
Objectives 1 and 2 form the basis of the Causality WP1, objectives 3 and 4 comprise the smoother WP2, and
objective 5 forms the contents of WP3.
The above program is very ambitious, aiming to generate step changes in our thinking about
causality and nonlinear data assimilation. The application is complex, high-dimensional, and highly nonlinear, allowing for
a thorough testing of all methodologies on a real problem, and crucial for our understanding
of the functioning of the ocean in the climate system.
The potential benefits for the geosciences and beyond are potentially enormous: the causality problem arises in all sciences
and a proper Bayesian context has the potential to enforce step changes in all these fields.
Exploring the model equations in causality questions is not new, but an exciting new idea can lead
to much more robust causality calculations.
(It also has to potential to derive new model equations based on causality, a very interesting
science area that we cannot pursue here.)
A fully nonlinear smoother will allow for much better reanalysis than available now.
Reanalysis are used extensively in atmospheric sciences for process studies, but are hampered now by
ad hoc changes to the system, linearity assumptions, and the lack of a proper uncertainty estimate.
If successful we will solve or greatly reduce all these problems.
Finally, by applying all newly developed techniques to the ocean area south of Africa we will be able to
unravel the causality structure, potentially solving an outstanding problem in the functioning of the ocean,
and with that in its functioning in the climate system. If successful the methods can be applied to other
ocean areas too, including the ocean as a whole, allowing for large changes in our fundamental understanding
of the ocean system.
The proposal consists of three main workpackages that work strongly together. WP1 develops causality strength measures
further and puts them into a Bayesian framework, WP2 develops a fully nonlinear data assimilation technique that
is smooth in time, and the results of both are used in WP3 in which causality in the complex high-dimensional
ocean system is investigated.
This WP consists of two strands of research, one on the conversion of causality strength to a Bayesian framework,
and one on exploring new ideas on using the model equations in determining causality.
I will work with one postdoc on each of them.
The goal is to find an estimate of the actual causality strength including its uncertainty in the form of a pdf, given all
information available.
If new information becomes available we can use Bayes Theorem again, in which the posterior
pdf of causality strength becomes our new prior pdf.
To use this framework we need to:
By exploring these measures in different small-scale systems in which the causality structure is known
I will explore the accuracy of each causality measure, including biases etc.
Comparisons like this are not new, but they are in the Bayesian context.
The pdfs in Bayes Theorem will come from an ensemble of model states.
We have to estimate pdfs from relatively small sample sizes, in at least 4 dimensional systems.
For our large-scale application we will be able to use a minimum of 200 ensemble members.
Assuming weekly sampling over a 25-year period,
our sample size is 200x25x52= 260,000, which is reasonable, but not overwhelming.
An important question is how that representation can be used most efficiently and several methods have been proposed.
Knuth (2006) and Knuth et al. (2006) provide optimal ways to generate accurate histograms from irregular data,
and methods for uncertainty quantification of the entropy and mutual information estimates.
Knuth et al (2006) also discuss the use of Gaussian Mixture models using Expectation Maximisation (see e.g. Bishop, 2006).
and both methods are compared on climate data in Knuth et al., (2008).
They show that the histogram method is too noisy, while the error estimates using the Gaussian Mixture model
are too narrow.
I will explore methods from statistical language modelling in which distributions modelling three variables
are smoothed with the distributions of two variables in a method called 'discounting', e.g. via Good-Turing
in combination with back-off models (e.g. Katz, 1987, Zhai, 2009).
I will also explore nearest-neighbor-based estimation of mutual information (Kraskov et al, 2004)
and in Transfer Entropy for neuroscience research (Vincente and Wibral, 2014), and Darbellay-Vajda (D-V)
adaptive partitioning of the samples, see e.g. Lee et al., (2012), from biomedical engineering,
but also ideas from machine learning,
engineering, business analytics, linguistic programming, engineering, and finance will be explored.
Large-deviation theory investigates the behaviour of rare events in complex high-dimensional systems,
and quite often an exponential behaviour of the probability of rare events is encountered.
The rare event is that the particles have to be close to a very large number of observations.
Vanden-Eijnden and Weare (2012, 2013) provide a way to infer particle trajectories that have equal weights by construction.
Two problems remain, the first being that the assumption is that all particles start from the same initial condition,
which is unrealistic, and second that their method is way too expensive to use in high-dimensional systems.
The expense comes from the fact that one has to run a separate 4Dvar for each time step to the end of the window,
making it a $T^2$ algorithm, in which $T$ is the window length.
The authors provide approximations that lead to algorithms fairly similar to the implicit particle filter of Chorin and Tu (2009).
This means that one runs a method like 4D-VAR on each particle.
Special in the application of these adjoint methods is that the initial condition for each particle is fixed, but errors in the model equations are included
(see also Van Leeuwen, 2009).
However, as mentioned above the implicit particle filter is degenerate for high-dimensional problems.
Firstly, with the help of postdoc 3 I will extend the theory to a situation where the initial conditions for the particles are drawn from a Gaussian,
and for the situation when the initial condition consists of a number of particles drawn from an arbitrary distribution.
In this way we will be able to find a full theoretical (but most likely not practical) solution to the nonlinear smoother problem.
This solution will be the starting point for approximations that will keep the weights of the particles equal,
connecting to Zhu and Van Leeuwen (2015).
We will explore that observations only influence the smoother solution for a finite time interval, the length of which depends on the
kind of observation. For instance sea-surface temperature observations encounter a short memory of perhaps a week, while sea-surface height observations have an influence that can last a month (Brusdal et al., 2003).
An issue with running a variational problem on each particle is that the adjoint of the model has to be known.
That adjoint is not available for the ocean model we will use, and generating it would be too demanding.
One idea is to explore the more flexible Ensemble Kalman Smoother (Van Leeuwen, 1999; Evensen and Van Leeuwen, 2000; Van Leeuwen, 2001), in which the ensemble itself is used to generate 4-dimensional covariances used in the data assimilation,
run iteratively to allow for nonlinearity.
Interestingly, one doesn't need to run the ensemble to full convergence, just a few cycles
will be enough in the proposal density.
Another approximation that avoids the adjoint comes from synchronisation theory.
The basic idea behind synchronisation is that one tries to synchronise the model with reality through the observations.
In practise this means that extra coupling terms are added to the model such that all Lyaponov exponents are
negative (see e.g. Szendro et al. 2009, Whartenby, Quinn, and Abarbanel, 2013).
More recently Rey et al. (2014) and An et al. (201, submitted) explored the use of
time-delayed observation vectors to increase the number of observations and report strong synchronisation with only a limited
number of observations in the Lorenz 95 model and a
256-dimensional nonlinear shallow-water model.
A problem with the above synchronisation procedures is that they are ad hoc: errors in the observations
are ignored, and also the model errors are either ignored or are treated in an ad-hoc way.
Also the delayed form uses the observations more than once, and that is only allowed when model-observation correlations are taken into account, which is not part of the synchronisation procedure. What needs to be done first is to embed the synchronisation idea into Bayes theorem, which is indeed our first step.
More specifically, one needs to view the synchronisation terms as part of a proposal density and take the associated weights into account.
This is quite similar to the relaxation proposal density in Van Leeuwen (2010), with this difference that we
will exploit the delay-time forcing which will help to constrain the system better between observation times.
Then I will explore how to synchronise unobserved variables.
Especially in the ocean the observation density is quite low. We tend to observe the fast-changing surface variables and not the deep slower-varying variables, but also the surface field is not completely sampled at the resolution at which we will run the ocean model.
I will exploit the spatial structure of the model error covariances for this problem.
A different much less developed path is exploring ideas from optimal transportation (El Moselhy and Marzouk, 2012),
which I will do with postdoc 4.
The idea is to try to find a transformation $g(..)$ from the prior particles $x_i$ to posterior particles $z_i$.
Together with postdoc 4 I will investigate application of the method over a time window between observations, fixing the starting point
of the particles to ensure a smooth evolution at observation times. Furthermore, we will explore different
minimisation formulations. Their is a huge literature on optimal transportation, and ideas from different fields will be explored.
We will explore the connection to Zhu and Van Leeuwen (2015) who also define a transformation from prior
to posterior particles but in their case the transformation is implicit.
We will also investigate iterative procedures to transform prior particles to posterior particles by defining
the transformation is pseudo time. Again a large field
opens up for exploration, and we will investigate a connection with large-deviation theory.
I will work with the two postdocs on large-deviation and synchronisation theory,
and on optimal transportation, pulling the work together, especially in year 3 to generate a full nonlinear particle smoother that can be used in high-dimensional systems. We start on simplified models like the Lorenz 1963 and 1996 models, moving towards the barotropic vorticity equation and multi-layer quasi-geostrophic models for ocean flows.
I will use the nested model configuration INALT01 of Biastoch (2008, 2009), that
consists of a global model with a resolution of $0.5^o$ with a nested model with horizontal resolution of $0.1^o$ around the southern tip of Africa reaching all the way to South America.
The total number of prognostic model variables is about 200 million and up to 200 members are needed to calculate the causality measures.
This part of the proposal is extremely computer intensive and a contribution to run-time costs is part of the proposal. The UK Natural Environment Research Council (NERC) supports further run-time costs and storage.
The first part of the work consists of porting the INALT01 model to the EMPIRE software system on the ARCHER supercomputer in the UK.
EMPIRE is a data-assimilation coding system developed in my group, and we are developing it to become the UK national data-assimilation framework for geoscientific research. Implemented are a suite of ensemble data-assimilation methods, like the stochastic EnKF (developed by Evensen and the PI in the 90s), the LETKF, 4DEnsVar, and several particle filter variants including the particle filter developed by Zhu and Van Leeuwen (2015).
EMPIRE communicates with the ocean model via MPI, which makes it a rather simple operation to couple the complex INALT01 model to it, typically taking a few days.
Biastoch (personal communication, 2015) has offered help with the set up and analysis.
We will initiate the ensemble by taking snap shots from a long model run.
Then a proper error model for errors in the model equations $Q$ has to be implemented.
It should reflect the {\em influence} of the missing physics on the model evolution.
This means $Q$ will have correlations over several grid scales and over time.
We will investigate how much time correlation is needed.
Using knowledge of the physical system and the model performance (see e.g. Van Sebille et al., 2009) specific error models are explored by generating ensembles and running them for relatively short times.
Furthermore, we will draw on experience on generating the background error covariance for numerical weather forecasting,
of which we have experts in my group.
Here my connections to both experts in numerical modelling and in the physics of the system are crucial.
Next we work on the observations. We start with altimeter observations and gradually include
more complicated observations, like mooring arrays operated by the physical oceanography groups in Utrecht and Texel, The Netherlands (De Ruijter, Ridderinkhof) , and in Miami, USA (Beal), with whom the PI has very good working relations, ship-born observations (from e.g. GoodHOPE; the PI has good working relations with Sabrina Speich, the PI of that consortium), and ARGO floats. By investigating the influence of each data type on the performance of the system we will be able to learn how information from observations flows trough the system, and fine tune the method. We will only use existing observational data sets in this proposal, exploiting e.g. the ESA ECV's.
Then the actual pdf, or rather its representation in terms of particles, is generated for a 25 year period covering
the satellite altimeter era. This is a huge task, asking full attention of the whole team.
The total amount of data generated by this reanalysis will be about 500 TB.
Then we concentrate on the causality strength calculations.
Our investigation includes, but is not limited to causal strength of the interocean exchange with the Agulhas current strength,
the strength and location of strong recirculation cell southeast of the tip of the continent,
the eddy activity in Mozambique Channel,
dipoles from the separating East Madagascar Current,
Antarctic Circumpolar Current strength and location,
large-scale zonal density gradients,
the number and size of Agulhas Rings,
the Indian Ocean subtropical gyre strength and location, and
larger scale modes of the Southern Ocean Supergyre.
The wealth of information in the pdf will also allow us to investigate other relations in this complex system,
both within this proposal and as spin-off to other projects and research groups.
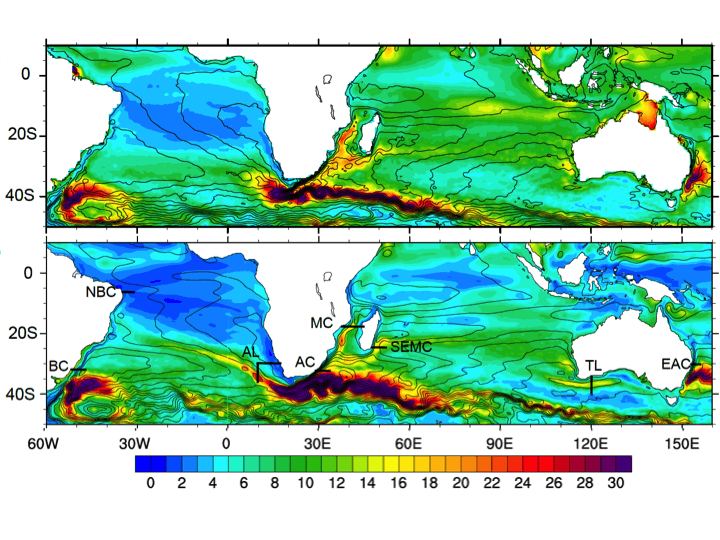 Figure 1: Sea-surface height standard deviation (cm) from satellite altimetry (top), and the state-of -the-art
ocean model POP at 0.1 degree resolution. The contours denote the mean dynamic topography.
Note the dominant turbulent area south of the African continent.
The model captures the main features but is off on several important details.
Figure 1: Sea-surface height standard deviation (cm) from satellite altimetry (top), and the state-of -the-art
ocean model POP at 0.1 degree resolution. The contours denote the mean dynamic topography.
Note the dominant turbulent area south of the African continent.
The model captures the main features but is off on several important details.
Nonlinear data assimilation
Recent developments in nonlinear data assimilation open possibilities to generate the pdf of the ocean system
and solve problems with pure model runs byi
Objectives
The main objective is to generate robust methods to determine causality strength in complex
highly nonlinear high-dimensional geophysical systems, and use this to a solve the interocean exchange
causality problem in the ocean area south of Africa.}
Potential future benefits
Methodology
WP1 Causal Strenght
WP2 Develop efficient nonlinear smoothers
WP3 Causality of the ocean