Introduction
Amongst the first successful attempts to model the atmosphere numerically was that of Charney, Fjorloft and von Neumann (1950) who integrated the barotropic vorticity equation (BVT) forward in time (the BVT is shown below with added second order difusion). This system is two-dimensional and so represents a major simplification of the full dynamic (Navier-Stokes) equations. Their procedure is essentially reproduced here (actually part of the MSc programme at Reading Univ.). Today we have the advantage of faster and more accessible computer power making our task easier than for the pioneers.
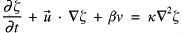
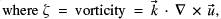
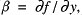
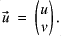
The initial and boundary conditions
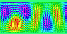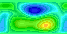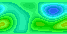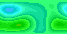
The geopotential height field (analagous to pressure) is specified at time t=0 and is subject throughout to periodic boundary conditions in x, and slip free boundary conditions at the edges in y. Our domain is a local area of 10000 x 5000 km at 45 degrees north. We integrate forward in real-time for 300 hours with a time step of 30 mins on a grid of linear resolution 150 km. Various quantities are output including the stream function (below - this is essentially the geopotential height - and hence can also be thought of as 'pressure-like'), and the vorticity.
The numerical scheme
We use a Centred-Time/Centred-Space (CTCS) grid-point numerical scheme (for stability) which is fully explicit. In order to minimize numerical dispersion, our model operates on a modified 'C'-grid.
Output 1: The stream function (frame time 2 hours)

Output 2: The vorticity (frame time 2 hours)

f=Earth (beta = df/dy)
K=2000.0 km^2/hour
Note: Thanks to Andrew Gregory for helping me debug my code.