Comparison of 'Inverse tests' 1 and 3
Friday 30th January 2006
Reminder of inverse tests process
The inverse tests done here check that the raw perturbations 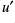 ,
, 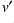 ,
, 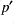 can be recovered after they have gone through the PV-based
can be recovered after they have gone through the PV-based 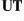 transforms.
transforms.
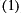
Does  ,
,  ,
, 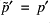 ?
?
The unbalanced part of the transforms
The calculation of 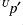 in the unbalanced part of the
in the unbalanced part of the 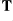 -transform (
-transform (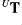 ) is tricky. It is found by solving the equation,
) is tricky. It is found by solving the equation,
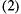
where  is the unbalanced
is the unbalanced  -transform, which gives the unbalanced contributions
-transform, which gives the unbalanced contributions 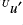 ,
, 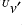 and
and 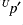 from the control vector element
from the control vector element 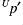 .
.
The generic formula for 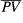 is,
is,
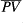 is needed on
is needed on 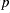 -points on the grid.
-points on the grid.
There are two ways of computing 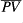 :
:
- If the known variables are
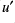 ,
, 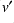 ,
, 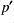 on their respective grid points, then
on their respective grid points, then
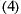
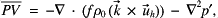
(where 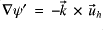 has been used). The first term is found naturally on
has been used). The first term is found naturally on 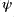 -points and the second term is found naturally on
-points and the second term is found naturally on 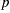 -points. The first term therefore has to be interpolated.
-points. The first term therefore has to be interpolated.
- If the known variables are
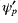 (streamfunction on
(streamfunction on 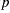 -points) and
-points) and 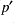 , then Eq. (3) can be computed with both terms on
, then Eq. (3) can be computed with both terms on 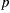 -points.
-points.
Method 1 is used to calculate the RHS of Eq. (2). Previous to mid January 06, method 1 was also used to calculate the LHS of Eq. (2). The smoothing that was done to change grid positioning was causing 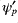 to show grid-point waves to compensate for the smoothing in the inversion (2). This is scheme A. A variable that occurs naturally in the
to show grid-point waves to compensate for the smoothing in the inversion (2). This is scheme A. A variable that occurs naturally in the 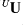 -transform is
-transform is 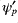 and so recently the code has been modified to compute the LHS using method 2 (with the RHS still using method 1). This is scheme B.
and so recently the code has been modified to compute the LHS using method 2 (with the RHS still using method 1). This is scheme B.
On my PV control variable web page,
- The inverse test that uses scheme B is inverse test 1.
- The inverse test that uses scheme A is inverse test 3.
See inverse tests section of this page. To see both tests together go to this page.
Comparing the schemes
In summary, the use of scheme B does not improve the inverse test results over scheme A.
The inverse tests use 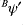 and
and 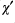 in addition to
in addition to 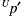 , so any problems may be due to these.
, so any problems may be due to these.
Shown in the web pages are 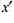 ,
, 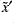 ,
, 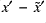 ,
, 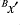 ,
, 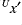 and
and 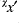 for
for 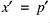 ,
, 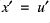 and
and 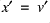 .
.
All showing horizontal plots at levels 1, 11 and 30, and a lat-height plot at the Greenwich meridian.
- The difference
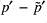 show smaller max and min values in scheme B than in scheme A (not at level 30 though), but the differences are more grainy in scheme B than in scheme A. This is seen especially in the lat-height plot.
show smaller max and min values in scheme B than in scheme A (not at level 30 though), but the differences are more grainy in scheme B than in scheme A. This is seen especially in the lat-height plot.
- Looking at the differences
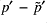 shows structure that is present in
shows structure that is present in 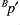 and
and 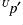 , but mainly in the latter. This may indicate that the unbalanced contribution to
, but mainly in the latter. This may indicate that the unbalanced contribution to 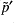 is mainly at fault.
is mainly at fault.
- The zonal winds from scheme B are comparable to those of scheme A. Sometimes better, sometimes worse. At level 1 there is less grid-wave structure in the meridional direction in
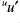 in scheme B than in scheme A (as required), but the zonal wind at the equator is still far too high.
in scheme B than in scheme A (as required), but the zonal wind at the equator is still far too high.
- Looking at the differences
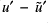 shows structure that is present in the contribution from
shows structure that is present in the contribution from 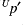 . This indicates that the unbalanced contribution to
. This indicates that the unbalanced contribution to 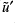 is mainly at fault.
is mainly at fault.
- Similar arguments apply to meridional wind, but there is no equator problem in either scheme A or B.
Next steps
- The LHS and RHS of Eq. (2) are computed using different methods in scheme B. The code that computes the RHS of Eq. (2) is more messy than it needs to be. I will simplify this (and may discover things that can be done better).
- I will run the
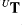 operator with far more iterations than at present (with scheme B) to see if the errors in the inverse problems reduce significantly.
operator with far more iterations than at present (with scheme B) to see if the errors in the inverse problems reduce significantly.
- I have not yet looked into the pole issues and I have not yet 'removed' the boundary layer (by copying winds at level 5 to lower levels).
![]() ,
, ![]() ,
, ![]() can be recovered after they have gone through the PV-based
can be recovered after they have gone through the PV-based ![]() transforms.
transforms.
![]()
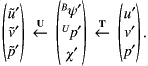
![]() ,
, ![]() ,
, ![]() ?
?
![]() in the unbalanced part of the
in the unbalanced part of the ![]() -transform (
-transform (![]() ) is tricky. It is found by solving the equation,
) is tricky. It is found by solving the equation,
![]()
![]()
![]() is the unbalanced
is the unbalanced ![]() -transform, which gives the unbalanced contributions
-transform, which gives the unbalanced contributions ![]() ,
, ![]() and
and ![]() from the control vector element
from the control vector element ![]() .
.
![]() is,
is,
![]()
![]()
![]() is needed on
is needed on ![]() -points on the grid.
-points on the grid.
![]() :
:
![]()
![]()
![]() has been used). The first term is found naturally on
has been used). The first term is found naturally on ![]() -points and the second term is found naturally on
-points and the second term is found naturally on ![]() -points. The first term therefore has to be interpolated.
-points. The first term therefore has to be interpolated.
![]() to show grid-point waves to compensate for the smoothing in the inversion (2). This is scheme A. A variable that occurs naturally in the
to show grid-point waves to compensate for the smoothing in the inversion (2). This is scheme A. A variable that occurs naturally in the ![]() -transform is
-transform is ![]() and so recently the code has been modified to compute the LHS using method 2 (with the RHS still using method 1). This is scheme B.
and so recently the code has been modified to compute the LHS using method 2 (with the RHS still using method 1). This is scheme B.
![]() and
and ![]() in addition to
in addition to ![]() , so any problems may be due to these.
, so any problems may be due to these.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() for
for ![]() ,
, ![]() and
and ![]() .
.