Software and User Guide

Last updated 17th February 2003

What is Kepler's equation?

Kepler's equation describes the classical motion of a mass in an inverse square gravitational field. It is derived from Newton's second law of motion. Although Kepler's equation ignores many body effects, it provides a simple yet useful approximation to the motion of the major planets of our solar system.

Kepler's equation will give the position of a planet in its orbit at a specified time, given certain information about the orbit such as its size and shape, and where the body was at an earlier time. We focus our attention on elliptical orbits. Such an orbit is described by its size, shape and orientation which are determined completely by six parameters.

These parameters are: the length of the semi major axis, (astronomical units), the eccentricity, (dimensionless), the inclination to the ecliptic, (degrees), the longitude of the ascending node, (degrees), the longitude of the perihelion, (degrees) and, the mean longitude, (degrees).

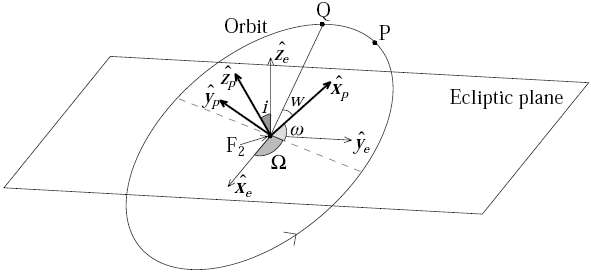
It is not crucial here to know what these parameters mean and how they are used (see standard astronomy texts, or our paper in the American Journal of Physics for this information). The future positions of a planet can be predicted by solving Kepler's equation using these parameters.

What are we doing when we 'invert' Kepler's equation?

It is useful to think of solving Kepler's equation as a forward problem - given the parameters and a set of times, we predict where the planet will be at those times. The inverse problem asks the reverse question. Given a set of observed positions (and the times that the observations were made), what are the six parameters? Inverse solutions are generally harder to solve than the forward approach (although the inverse method itself requires the existence of the forward solution). The observations that are fed into the 'inversion' will come from measurements which will be subject to observation errors, which the inversion must account for.

The method works by minimizing a cost function which is a function of the six orbital parameters. The cost function is a positive scalar that is a measure of the misfit (or cost) due to discrepancies between the model's version of the observations (found by solving Kepler's equation) and the observations themselves. All observations have errors, and so the cost function can never be zero.

Inverse methods are useful in general as they allow information to be inferred about unknown parameters that cannot be measured directly (the six orbital parameters in this case). Instead, measurements of observables (the planetary positions in this case) are taken. The relationship between the unknown parameters and the observables is forged through the forward solution, or 'forward model'. This whole procedure is known as inverse modelling. Other examples are given in the paper, and the scope of such techniques goes well beyond those examples.

Our astronomy inverse model demonstration

(See the notes for use below.)

Given a number of measurements of a planet made by an Earth-bound observer, the inverse method (provided in Fortran-77 below) will attempt to infer the six orbital parameters that are consistent optimally with the observations. This is done using an iterative 'trial and error' or 'predict and correct' manner that is assumed to converge to the optimal solution. This is done by minimizing a cost function formulated by the method of least squares. This method goes under the name of optimization, data assimilation, inverse modelling or data fusion.

Our software will accept altitude/azimuth measurements of the planet, or right ascension/declination measurements. At the very least, three pairs of such observations are necessary, although we recommend that at least 10 pairs are used. Apart from inverting the observations to yield orbital parameters, the code can be run in other modes, e.g. that will plot past and future trajectories of the planet with the determined parameters.

The user guide for the inverse Kepler software

Downloading the files and compiling the code.

Download the following files to your computer system (click on each of them in turn and use your browser to save them on your system):

• KeplerAssim.f This is the fortran-77 source code. No libraries are required.
• VenusObs This is an example input file to the program. It contains information on how the program is to be run and the observations used.

You will need to compile the source code yourself to get an executable program that will run on your system. You will need a fortran-77 or fortran-90 compiler. The compilation command may (e.g. on UNIX systems) look something like,

f77 KeplerAssim.f -o KeplerAssim.out

This names the executable "KeplerAssim.out".

The run modes - "XSEC", "ANAL", "RECO" and "TRAJ"

The software may be run in any of four modes, as specified in the input file.

• The "XSEC" mode outputs cross-sections through the six dimensional cost function centred on a specified set of parameters. This is done by varying each parameter in turn over a range. This mode is useful in pre-processing the observations in order to arrive at a good initial guess at the set of parameters. This guess is then refined using the "ANAL" mode (below).
• "ANAL" is the analysis mode that objectively minimizes the cost function to arrive at the optimal set of parameters. It also estimates the errors in the parameters.
• "TRAJ" outputs predicted trajectories of a planet given its orbital parameters. This is useful firstly to test consistency with existing observations once they have been analysed, and secondly to make predictions regarding the future positions of the planet.
• "RECO" stands for reconfiguration and converts observations which have been provided as alt/azi measurements to RA/dec type. This is an alternative form for the observations which can themselves be analysed by the program using the "XSEC" and "ANAL" modes above. (This is a little used mode of the program and is not expected to yield good results - for this reason, use of this mode is not documented here).

The use of each mode (except the last one) are described in the forthcoming sections of this document.

The input file format

The input file is a text file that can be edited with any text editor program. A typical input file will resemble the following:

# ======================================================================
# Real alt/azi observations pertaining to Venus
# Ross Bannister, Data Assimilation Research Centre, Reading, UK
# ======================================================================
# AstroObs input file for Astronomical Data Assimilation
# ======================================================================
# longitude (+/-1, degrees, minutes)
# latitude (+/-1, degrees, minutes)
# First guess at orbital elements a, e, i, Omega, omega-bar, epsilon
# Run modes:
# XSEC : Generate cost function cross sections
# ANAL : Perform variational analysis
# RECO : Reconfigure input file (Alt/azi to RA/dec)
# TRAJ : Use input parameters to generate RA/dec trajectory
# Bracket for length of semi-major axis (AU) a(min), a(max)
# Bracket for inclination of orbit to ecliptic (degrees) i(min), i(max)
#----------------------------------------------------------------------
# Sample Input File: for each observation ...
# Type of observation 1 or 2 (see below)
# Times in UT (year, month, day, hour, min)
# E.g. 2001, 02, 05, 00, 14
# Type 1: observation of type RA h, m, error (m)
# Dec d, m, error (m)
# Type 2: observation of type alt (d), error (d)
# azi (d), error (d)
# ----- END OF HEADER --------------------------------------------------
#### PRELIMINARY DETAILS ##############################################
#Longitude
-1 0 58
#Latitude
1 51 27
#First guess for orbital parameters a, e, i, Omega, omega-bar, epsilon
0.7 0.1 5.0 90.0 100.0 110.0
#Run mode, XSEC, ANAL, RECO, TRAJ
ANAL
#Verbose? 1=on, 0=off
0
#Range of length of semi-major axis (AU)
0.10000 2.00000
#Range of inclination (degrees)
0. 45.00000
#Convergence cutoff in length of increment
0.0001
#Maximum number of iterations
100
#Number of iterations performing partial minimization
0
#Perform refraction correction 1=on, 0=off (NOT YET IMPLEMENTED)
0
#Include 2nd derriv of forward model in Hessian 1=on, 0=off
0
#======================================================================
#### OBSERVATION DETAILS FOLLOW #######################################
2
2001 02 13 18 58
23.0 0.5
251.4 2.0
#-----------------------------------
2
2001 07 26 03 01
14.5 1.5
73.9 1.2
#-----------------------------------
2
2001 08 21 04 21
22.2 1.5
84.1 1.2
#-----------------------------------
2
2001 09 05 04 18
16.2 1.5
82.3 1.2
#-----------------------------------
2
2002 04 07 19 39
7.4 1.5
281.3 1.2
#-----------------------------------
2
2002 05 30 20 50
16.6 1.5
289.6 1.2
#-----------------------------------
2
2002 06 17 21 29
11.9 1.5
290.7 1.2
#-----------------------------------
2
2002 06 23 21 10
13.4 1.5
285.3 1.2
#-----------------------------------
2
2002 07 16 21 11
6.0 1.5
281.4 1.2
#-----------------------------------
2
2002 07 25 20 19
10.2 1.5
264.8 1.2
#-----------------------------------
2
2002 07 29 19 58
13.7 1.5
261.7 1.2
#-----------------------------------
2
2002 09 10 18 01
9.9 1.5
228.5 1.2
#-----------------------------------
2
2002 12 19 07 03
22.1 1.5
150.5 1.2
#-----------------------------------
2
2003 02 15 07 04
11.7 1.5
145.6 1.2

(Note that the name of this file is arbitrary - the user will be prompted for the name when the program is run.)

Lines starting with a hash (#) are comment lines. The format of the file is very strict (with respect to the presence of the correct number of comment lines, the number of pieces of information in each line, etc). Data of the correct format must be put in each section. Not all sections of the file are used by all run modes, and so unused lines should be padded with arbitrary data (e.g. zeros). The required information for the important run modes is documented below.

The file is divided into three parts. The first part consists entirely of comment lines, and serves to specify (for the user's benefit) the contents of this file, and as a reminder of the format of the rest of the file. The second part allows the user to specify some constants used by the program, how the program is to be run (the run mode) and other working constraints. The final part contains the planetary observations and their estimated uncertainties.

Entries in the input file that are common to all run modes

Some of the entries in the input file are used by all run modes and require explanation.

The longitude and latitude of the observer.

It is assumed that all planetary observations are made at one location. Three integers are required each to specify the longitude and latitude. The first integer represents the sign of the longitude (+1 is east of Greenwich, -1 is west) or latitude (+1 is for the northern hemisphere, -1 is the southern hemisphere), the second is the integer part of the longitude or latitude degrees, and the third is the remaining minutes of arc.

The verbose switch

If verbose is set to on (1), it will stream detailed progress and technical information to the standard output (this is the screen unless specified otherwise by your computer's operating system). Sometimes this is useful, other times it is a nuisance, in which case it can be turned off (0).

Observations

Observations are specified by the time/date of the observation, and two angles (either right ascension and declination or altitude and azimuth). This information is provided in four lines per observation, with each set of four lines separated by a comment line. The first line specifies the type of observation (1 is for the RA/dec variety, 2 is for the alt/azi kind). The next line is the date in the format

yyyy mo dy hr mn

where yyyy is the full year (e.g. 2002), mo is the month number (1 is January, etc.), dy is the day of the month, hr is the hour, and mn in the minute. All times must be specified in universal time (same as GMT). The next two lines specify the planets observed position, and their format depends upon the type of observation. For type 1 observations (RA/dec) these two lines should be:

hr mn err
de mn err

where the hr, de and mn are integers giving the hour and min for the RA (line 1) and degrees and minutes in the case of declination (line 2). The error in each case is in arc minutes, which is a real number and so should contain a decimal point. For type 2 observations (alt/azi) these two lines should be:

de err
de err

where all information (altitude (line 1) and azimuth (line 2) values and errors) are real numbers specified in degrees.

Note that at least three observations (six pieces of information) are required to determine an orbit, although the information contained in only three measurements will probably yield a very poor analysis.

The purpose and use of each important run mode is now described.

Looking at cross sections of the cost function ("XSEC" mode)

In order to proceed with the inversion, a guess of the orbital parameters is required. This is sometimes tricky to obtain, especially if no other information is known about the planet. The guess must be close to the global minimum of the cost function. The cost function will probably have multiple local minima, and so it is helpful to look at cross sections through the six-dimensional cost function field to choose first-guess parameters that are in the right ballpark.

Completing the input file

The "XSEC" mode will allow the user to inspect such cross sections. The input file should be prepared in the following way (refer to the above example input file as a guide):

• Set the longitude and latitude to those of the observer (as format above).
• The 'first guess' for the six parameters refers to the centre of the cross section plots when the program is run in cross section mode. For an inferior planet, set this line to something like:
  0.7 0.001 0.0 0.0 0.0 0.0
  for a superior planet use something like:
  4.0 0.001 0.0 0.0 0.0 0.0
  or if it is not known whether the planet is closer or further from the Sun than the Earth is use something like:
  1.0 0.001 0.0 0.0 0.0 0.0
  The parameters correspond to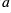 , , 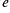, , 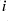, 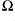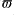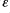(see the start of this guide).
• The run mode should be set to "XSEC".
• The verbose switch is best set to on (1) so that you can see the progress of the program on the screen.
• Two of the parameters need a range specified when plotting the cross sections. The length range of the semi-major axis (in astronomical units) depends again on the distance of the planet from the Sun. For an inferior planet use:
  0.1 1.0
  for a superior planet use:
  1.0 35.0
  (assuming that the planet's semi-major axis length is no greater than 35 astronomical units). If it is not known whether the planet is closer or further from the Sun than the Earth is use:
  0.1 35.0
  Set the range of the inclination to the following:
  0. 45.00000
  (it is unlikely that the inclination of the planet is greater than 45 degrees).
• The next five entries are not used by the cross section mode, but make sure that they are padded with arbitrary numbers (e.g. 0.0 for the convergence cut-off and 0 for the remaining four entries).
• Enter the observations as described above.

The output files

There are six output files (labelled "Param#" where "#" is 1,2,...,6), each containing a cross section through the cost function field. For file #, parameter # is varied over some range while the other five parameters are held to those values requested in the input file. The parameter number corresponds to the parameter in the way shown near the start of this document.

Each ASCII output file is comprised of the following lines:

value of variable parameter, value of cost function

These files can be plotted, and the parameters close to the 'global minimum' should be recorded. The 'XSEC' mode should be re-run with these new parameters in the input file to check for consistency (due to the complicated dependence of the cost function on each parameter and the limited information contained in the cross sections, the position of the 'global minimum' may change). This procedure may have to be repeated several times until the global minimum identified by this procedure remains roughly in the same position in parameter space.

Inverting the observations with Kepler's equation ("ANAL" mode)

The run mode "ANAL" refines the guess of the six orbital parameters to yield an analysed set of parameters that are consistent, via Kepler's equation and within the error tolerances, of the observations.

Completing the input file

The "ANAL" mode is intended to iteratively converge to the optimal set of parameters, by incrementally reducing the value of the cost function. This may take several hundred or thousand iterations using the simple algorithm implemented. The input should be prepared in the following way.

• Set the longitude and latitude to those of the observer (as format above).
• The 'first guess' for the six parameters is required. Unless a-priori information is known about the planet's orbit, follow the procedure of plotting cross section of the cost function as outlined above to obtain a first guess. An example first guess might be the following:
  0.7 0.007 3.0 75.0 130.0 180.0
  The parameters correspond to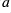 , , 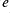, , 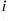, 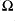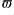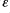(see the start of this guide).
• The run mode should be set to "ANAL"
• The verbose switch is best set to off (0) unless the program runs into difficulty in which case detailed diagnostic information can be output by turning on the verbose mode (1) - understanding verbose output however requires a detailed knowledge of the program workings.
• Two of the parameters need a range specified, which are used by an initial (and optional) partial minimization stage of the minimization algorithm. These are the length of the semi-major axis and the inclination. The partial minimization is performed, if activated (see below), within these ranges. The length range of the semi-major axis (in astronomical units) depends again on the distance of the planet from the Sun. For an inferior planet use:
  0.1 1.0
  for a superior planet use:
  1.0 35.0
  (assuming that the planet's semi-major axis length is no greater than 35 astronomical units). If it is not known whether the planet is closer or further from the Sun than the Earth is use:
  0.1 35.0
  Set the range of the inclination to the following:
  0. 45.00000
  (it is unlikely that the inclination of the planet is greater than 45 degrees).
• The convergence cutoff controls when the minimization is complete. The system will be taken as 'converged' when the length of the increment vector 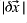(where 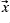is the six-element parameter vector) is less than the value specified in this part of the input file.
• Just in case that the system is not converging, the maximum number of iterations can be set here.
• During the first few iterations the computer can be made to perform preliminary partial minimizations by varying only the inclination and then only the semi-major axis length. The number of iterations at the start of the minimization that use the partial minimization can be set here. If partial minimization is not required then set this parameter to 0.
• Biases in the alt/azi observations are caused by atmospheric refraction. These can be corrected for, although the code to do this has not yet been implemented. Set this entry to 0.
• Although the forward model is a non-linear function of the orbital parameters, the priniciple behind the inversion process is to solve many linearized problems until the answer converges. This means that only first derivatives of the observations with respect to the parameters need be included in the Hessian of the problem. Second derivatives can be included by switching on (1) the next switch in the input file. It will normally be set to off (0) though.
• The remaining part of the input file allows the observations to be specified. See the above section for the format of observational data.

The Output files:

Apart from the information displayed on the standard output (usually the screen), the analysis run mode will output a file, "Convergence". This gives information on the parameters as the algorithm descends down the cost function field. Each line (except the last two lines of information) has the format,

iteration No, , , , , , , ,

(where is the value of the cost function at the state ). Below the analysed values will be the corresponding analysis standard errors,

, , , , ,

(where is the standard error field). Below the errors are the six eigenvalues of the final Hessian evaluation. This allows one to check the conditioning of the problem.

Plotting trajectories ("TRAJ" mode)

For a set of known orbital parameters, it is possible to compare the real observations to the ones that are predicted. It is also possible to calculate planetary trajectories during the period that the observations were taken, and also into the future.

Completing the input file

The "TRAJ" mode is intended to allow real and predicted observations to be compared and also to calculate planetary trajectories. To make the observation comparison and to compute trajectories over the period that the observations were taken, complete the input file according to the following.

• Set the longitude and latitude to those of the observer (as format above).
• Put the six, known orbital parameters under the section used in the other modes for the first guess parameters..
• Set the run mode to "TRAJ".
• Turn the verbose mode to on (1) - this is not vital however.
• The next seven entries are not used by the "TRAJ" run mode, so they can be either left with what is there already, or padded with zeros (something must be present as the fields are read in by the program anyway).
• Put the observations at the end of the input file in the form specified above.

Output files

Two files are output from this run mode. The file "TrajPoints" has one line per observation and has the following format:

time, RA(obs), dec(obs), RA(model), dec(model), RA(obs-model), dec(obs-model), alt(obs), azi(obs), alt(model), azi(model), alt(obs-model), azi(obs-model), obs type

where time is the time in days since 1st Jan 1990, RA fields are in hours, dec, alt and azi fields are in degrees, and obs type is either "RA/dec" or "alt/azi". Observations ("obs") and model observations ("model" - found from the parameters input) are provided in both RA/dec and alt/azi forms and appropriate conversions are made program so that both versions can be given.

For the "TrajCont" file, the computer divides the time between the first and last observations into 250 intervals. For each time, the computer predicts and outputs the following line of information, all according to the six parameters input:

time, RA, dec, x, y, z

where time is the time in days since 1st Jan 1990, RA is in hours, dec is in degrees, and is the position vector (in astronomical units) of the planet in the ecliptic plane.

If the information required is not over the observation period, but for some future period, then modify the input file in the following way.

• Delete the observations.
• The two future dates bounding the trajectory period are input into the computer by adding two bogus observations. The important information is in the two dates. The observation's types and values are arbitrary, but information must be placed in the correct format to pad out the input file.

Useful information is contained in the "TrajCont" file. The "TrajPoints" file can be discarded for future trajectories.

Use of the code

The code may be used freely as long as it is used for only academic or teaching use, and that we are acknowledged. Please let us know if you use the code.

References

Sterne T.E., An introduction to celestial mechanics (Interscience Publishers Ltd., New York, 1960).

Bannister R.N., The method of least squares used to invert an orbit problem (American Journal of Physics 71 (12) pp. 1268-1275 (2003)). Postscript here.