Ross Bannister, CGAM, Dept. of Meteorology, University of Reading, UK.
1. Contents 1
2. The primitive equations 1
2.1 Independent of the co-ordinate system 1
2.2 Use of the stress tensor 3
2.3 The Coriolis force 5
2.4 Cartesian co-ordinates
2.5 Spherical co-ordinates
2.6 Pressure co-ordinates
2.7 Potential temperature co-ordinates
2.8 Log-pressure co-ordinates
3. Derived quantities
4. Approximations
4.1 Geostrophic
4.2 Barotropic equations
4.3 Baroclinic stratification
4.4 Quasi-geostrophic approximation
The primitive eqs. are comprised of five coupled eqs.: three momentum eq., the continuity eq. and the thermodynamic eq. The three momentum eqs. are most conveniently represented in vector form:
The operator 
is the Lagrangian derivative linking the Lagrangian and Eulerian frameworks,
is velocity, 
is the gravitational acceleration, 
is density, 
is pressure, 
is the angular velocity of the Earth and 
is the drag force. The drag force is often assumed to be related to the stress tensor, 
, through 
(see §2.2). The terms of the momentum eqs. (1) originate respectively from gravity, pressure gradients, Coriolis force and friction. The form of the Coriolis force will become more explicit in the specific co-ordinate systems to be described below. The vertical direction is special as forces acting in this direction are highly balanced. Sometimes the vertical momentum eq. is replaced with the hydrostatic balance eq., 
(where 
is the vertical component of velocity). Ignoring drag and the vertical component of the Coriolis force (which is small, see §2.3), hydrostatic balance translates into,
In a Lagrangian sense the continuity eq. is written as,
but is more usually expressed with the Eulerian derivative,
If 
is independent of, or very weakly dependent upon, position, it can be taken outside the divergence operator. In each case ((4) and (5)) the time derivative 
for an incompressible atmosphere.
The thermodynamic eq. is a statement of the first law of thermodynamics (conservation of energy) and has a number of representations. In terms of temperature, 
, the thermodynamic eq.,
represents changes in internal energy (of an air parcel) due to adiabatic heating, heat fluxes and pseudo adiabatic heating (in eq. (6), 
is the specific heat capacity of air at constant volume). Adiabatic warming (first term on the right hand side) is due to changes in the volume of the air parcel (e.g. through ascent). It has been written as the divergence of the velocity field, but is related to changes in volume (via density changes) through continuity (eq. (4)). The heat flux, 
, has radiation 
and diffusion 
components (second and third terms) of which the radiation is a major mechanism for diabatic heating. In the diffusion term, 
is the diffusion co-efficient. The last term is a representation of latent heat exchange where 
is the rate of latent heat release per unit mass. Alternatively, the thermodynamic eq. may be expressed in terms of potential temperature, 
. Since 
implicitly includes adiabatic warming, the resulting eq. is slightly more compact. (eq. (10)). Potential temperature is defined,
where 
is the reference pressure of 1000 hPa, and 
is a dimensionless parameter. For the ideal dry gas, 
. In order to transform eq. (6) with 
as the prognostic variable in place of 
, we make use of the first law of thermodynamics (time differentiated following an air parcel),
where 
is the specific internal energy, 
is the specific heat energy supplied (diabatic heating) and 
is the specific volume. We substitute the following,
where in the last expression, eq. (5) has been used. Inserting these into eq. (8) and multiplying by 
gives,
Eliminating 
between eqs. (6) and (9) gives,
Associated with the five primitive eqs. ((1), (4) and (6)) are five unknowns (
). It is therefore possible (at least in principle) to solve the prognostic eqs. forward in time given suitable initial conditions. Note that 
may also be considered to be an unknown, but is related to 
and 
through the eq. of state of an ideal gas, 
.
The general description of fluid stresses sometimes involves the stress tensor, 
. Recall that formally, stress has dimensions of force per unit area, but the forces need not be acting in a direction perpendicular to the area face. 
is a three-dimensional rank-two tensor consisting of nine elements, labelled by 
. These have the form,
(see fig. 1). This element represents the force,
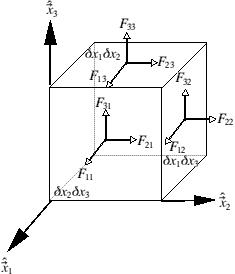
Fig. 1: The nine components of the stress tensor are related to the forces acting through the faces shown. The unit vectors 
and 
define the orthogonal co-ordinate system.
where the magnitude of the force acting as a result of this tensor element is 
, which is a function only of 
within the element. The diagonal components of 
are called the 'normal stresses' because they represent forces acting normal to the faces they act on. Off-diagonal elements are 'shear stresses'. Two important means of using the stress tensor are outlined. In the first application, we calculate the force per unit area acting through a particular face. Given a unit vector, 
, pointing normal to a chosen face (this does not have to be one of the basis vectors - the cube shown in fig. 1 is a construct only and there is not necessarily anything special about the choice of 
, 
and 
), we find that the force per unit area as represented by 
acting on the face normal to 
is,
where the rules of matrix mechanics apply to the action of the tensor on the vector. As an example, and to check the consistency of rule (13), consider the case when 
is one of the basis vectors. Let 
, then eq. (13) becomes,
which indeed contains the components of the forces acting through this face (which is how the stress tensor itself is set-up). Eq. (13) provides a convenient way of expressing the stress tensor in a different representation. The problem: given the stress tensor pertaining in a given representation (i.e. the components in eq. (12) and the vectors 
, 
and 
, what are the components of the stress tensor, 
in a new representation, 
, 
and 
? The dependence of the new vectors in terms of the original set must be made explicit. The transformation is contained in the rotation matrix 
of which the rows define the new unit vectors (perpendicular to the new faces),
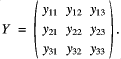
Thus, any vector in the 
-representation, 
is transformed into the 
-representation on action by eq. (14), i.e. 
. Obtaining the stress tensor in this new representation involves acting on each newly defined 'face' with 
in the manner of eq. (13), 
(
means transpose) and then projecting the resulting matrix of forces onto the new unit vectors (i.e. operate with matrix 
). In the 
-representation, the stress tensor is,
This structure is common to many applications of tensors and matrices when changing the basis.
In the second application of the stress tensor, which is of direct relevance to the momentum equations, we examine the operation 
. In the Cartesian system of unit vectors, 
, 
and 
, the result is the vector,
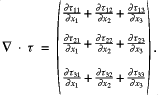
By noting the definition of 
from eq. (12) and multiplying by the volume of the fluid element, 
, this becomes,
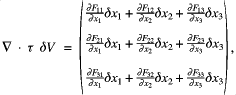
which is the net force acting on the fluid element due to all of the complications inherent in the stress tensor.
The Coriolis force for a fluid element of volume 
and density 
moving with velocity 
in a rotating frame of reference (rotation rate 
) is most generally written as 
. In the primitive eqs., its form is often simplified. There are many alternative ways in which the Coriolis force acting on an element is expressed. Some involve approximations.
Perhaps the simplest means of expressing the Coriolis force exactly is to first project 
onto the local radial, 
, and tangential, 
, unit vectors positioned at latitude 
(see fig. 2). Due to longitudinal symmetry, the longitude is not important. This is done via the rotation matrix in eq. (18) which acts on a co-ordinate system of the page (with components right, up and out of the page),
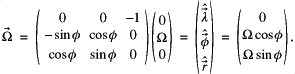
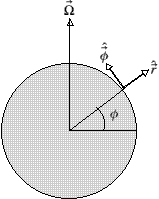Fig. 2: The Coriolis force, 
is easily translated onto the local radial and tangential unit vectors at latitude 
. 
is parallel, by definition, to the axis of rotation of the Earth.
Performing the calculation for the Coriolis force in these local co-ordinates gives,
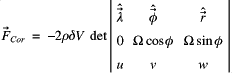
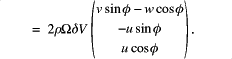
Usually only the horizontal components of the vector fields are associated with the Coriolis force. The vertical component of velocity is often neglected as 
, and the vertical component of the force itself is often ignored due to the strong vertical balance in operation. Dropping these terms leaves,
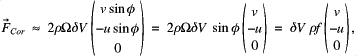
is the Coriolis parameter. This form of the Coriolis force is most relevant in spherical co-ordinates, but finds itself used also in quasi-Cartesian systems approximating a region of the globe as a plane (often under the 
- or 
-plane approximation). In the 
-plane approximation, the Coriolis parameter is treated as a constant, 
, where the system is centred upon latitude 
. Linear corrections are introduced in the 
-plane approximation where 
takes the form, 
where 
, and where 
is the radius of the Earth.