Ross Bannister, April 2001
Note the momentum equations,
and the continuity equation,
where the Lagrangian derivative has been used in the last line. We shall concentrate on rewriting the left hand side of Eqs. (1) under special conditions. If the fluid is incompressible (
), then Eq. (3) says that the fluid flow is nondivergent, and we can write the left hand side of Eqs. (1) in their so-called flux form.
This is easiest to see if we treat each momentum component separately. Demonstrating this with the 
-component,
Note the following expansion,
The last line is true under incompressible circumstances. Eq. (5) can be used to express Eq. (4) as the following,
which is the 
-momentum equation in flux form. Similarly for the 
- and 
-components of the momentum Eqs. (1),
It is not immediately clear to see how to express the three components in a compressed form, analogous to Eqs. (1). To do this we use the tensor product which yields a matrix as demonstrated by the following,
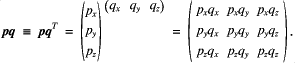
This is contrasted to the scalar product, 
. The momentum Eqs. (1) can be written in flux form using the tensor product,
from which the three components Eqs. (6), (7) and (8) can be recovered by considering the respective columns of Eq. (10) in turn. The tensor product, Eq. (9) is implied whenever two vectors are written side-by-side.