NUMERICAL SOLUTION IN THE LAGRANGE FORMULATION
Ross Bannister, June 2001
The double pendulum consists of two sections. Suspended from a fixed point is a mass, 
constrained to be a distance 
from that point, but is allowed to vary its orientation (
from the vertical). A second mass, 
is suspended a further distance 
from the first mass and it too has an angular degree of freedom, being an angle 
from the vertical at any instant. The physical system is illustrated in Fig. 1 (the system is in a gravitational field of magnitude 
, directed downwards).
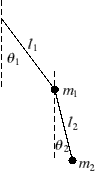
Figure 1: The double pendulum set-up. The lengths 
and 
, and the masses 
and 
are fixed. The system has the degrees of freedom 
and 
.
The Lagrangian is defined as 
, where 
and 
are expressions for the kinetic and potential energies respectively. In the Lagrange formulation, 
satisfies Lagrange's equations which determine the time evolution of the system. These are given later. The components of 
are,
In Eq. (1.2), the 
and 
refer to the positions of the respective masses (the dots refer to their rates of change and so the choice of origin is irrelevant). We require Eq. (1.2) to be written in terms of angles and so we exploit the transformations (we now choose the origin to be the fixed point),
Inserting Eqs. (1.3) to (1.6) into Eq. (1.2) (and simplifying), the Lagrangian becomes,
For each degree of freedom, there is an equation of motion. For degree 
this is,
where in the case of the double pendulum, 
. The 
and the 
represent separate variables. Eqs. (2.1) are coupled second order equations. This is apparent if the total time derivative is expanded by the chain rule,
where 
. The sets of partial derivatives can be represented as matrices 
and 
. Let,
(the components of these matrices, and the right-hand-sides of Eqs. (2.2) are given in the appendix). Equations 2.2 can then be written as,
with the different 
represented by the different rows of this matrix equation.
For the purposes of numerical solution, the equations of motion are best represented as a set of first order equations. Let 
. This has the consequence that 
. Writing the state vector with the four components 
and 
, and the equation set becomes,
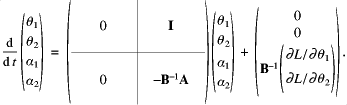
In Eq. (3.1), each quadrant of the large matrix is itself a 
matrix. The top two rows are simply a definition of the change of variables, and the bottom two rows are the Lagrangian equations of motion (Eq. (2.4) rearranged). The inverse of 
is easy to calculate as the matrix is of only small rank (see the appendix).
For convenience we will write Eq. (3.1) in the simplified form of,
where the vector 
represents the four variables pertaining to the angles and their rates of change. The 
matrix 
and the vector 
are functions of the state variable 
(denoted by the subscript). We will solve the equations using the standard fourth order Runge-Kutta solution [1]. This has five stages,
1. Calculate 
: 
2. Calculate 
: 
3. Calculate 
: 
4. Calculate 
: 
5. Calculate 
: 
The value 
is set by the initial conditions (as specified).
We note the partial derivatives of 
(Eq. (1.7)),
Noteworthy also is the inverse of matrix 
. If,
then the inverse is,
[1] Press W.H., Teukolsky S.A., Vettering W.T., Flannery B.P., Numerical Recipes in Fortran (section 16.1), Cambridge University Press (1994).