(and Application to Differentiating the Cost Function)
Ross Bannister, December 2000/August 2001
Let ![]() , where
, where ![]() is a matrix. Prove that the vector derivative
is a matrix. Prove that the vector derivative ![]() .
.
Expanding out the linear operator expression,
![]()
![]()
With the vector derivative, ![]() defined as the row vector,
defined as the row vector,
![]()
![]()
the definition of ![]() is,
is,
![]()
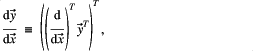
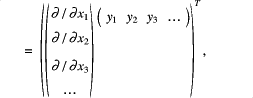
![]()
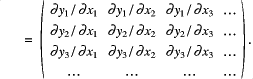
Differentiating Eq. (1.1) with respect to an arbitrary component gives us information regarding the matrix elements of Eq. (1.4),
![]()
![]()
Thus, by the definition of Eq. (1.3), we have proved that ![]() .
.
Consider the cost function as used in variational data assimilation. This is comprised of a background term and an observation term. Respectively these are:
![]()
![]()
where ![]() is the background term with error covariance matrix
is the background term with error covariance matrix ![]() ,
, ![]() is the variational state,
is the variational state, ![]() is the vector of observations with error covariance matrix
is the vector of observations with error covariance matrix ![]() and
and ![]() is the forward model. This is a vector functional of the variational state and is the model's prediction of the observations. When the cost function is minimized, the variational state is known as the analysis. The cost function is usually written in incremental form, that is with the variational state written as an increment to a linearization state:
is the forward model. This is a vector functional of the variational state and is the model's prediction of the observations. When the cost function is minimized, the variational state is known as the analysis. The cost function is usually written in incremental form, that is with the variational state written as an increment to a linearization state:
![]()
![]()
where
![]()
![]()
![]()
![]()
have been substituted into Eq. (2.1) to obtain Eq. (2.2).
In order to differentiate Eq. (2.1), we find it easiest to first expand the matrix notation into explicit summation form:
![]()
![]()
In Eq. (2.5), we note that a term like ![]() is the
is the ![]() ) th component of
) th component of ![]() (and not the reciprocal of the
(and not the reciprocal of the ![]() th component of
th component of ![]() ). Differentiate with respect to the
). Differentiate with respect to the ![]() th component of
th component of ![]() :
:
![]()
![]()
![]()
where ![]() is the kronecker delta function. Exploiting the fact that the error covariance matrices are symmetric, and using the following substitution,
is the kronecker delta function. Exploiting the fact that the error covariance matrices are symmetric, and using the following substitution,
![]()
![]()
(which is effectively a linearization of the forward model), we arrive at,
![]()
![]()
This can now be compactly written back in matrix notation by assembling a column vector of partial derivatives from all values of the index ![]() ,
,
![]()
![]()
The first derivative is thus a vector. The second derivative is a matrix and is called the Hessian. In order to find the Hessian matrix, ![]() , we return to Eq. (2.8) and differentiate with respect to another component of the variational state,
, we return to Eq. (2.8) and differentiate with respect to another component of the variational state, ![]() ,
,
![]()
![]()
![]()
![]()
which may, once more, be written in the compact matrix notation,
![]()
![]()
Sometimes, for reasons of preconditioning, the variational procedure is performed in a space which is a transformation of the ![]() space used above. Let a new
space used above. Let a new ![]() space be defined by the transformations,
space be defined by the transformations,
![]()
![]()
![]()
![]()
where ![]() . These operators may represent either rotations or scalings (or both). The first and second derivatives with respect to
. These operators may represent either rotations or scalings (or both). The first and second derivatives with respect to ![]() are shown below. Also are the
are shown below. Also are the ![]() derivatives summarized from above.
derivatives summarized from above.
![]() derivatives
derivatives
![]()
![]()
![]() derivatives
derivatives
![]()
![]()