, which is a measure of the misfit between the current estimate and the incoming information.
Part I: Forward Models and Adjoints for Layer Averaging
DARC Technical Report No. 3
Ross N. Bannister
Data Assimilation Research Centre, University of Reading, UK
Last revised 27th January 2002
The starting point of atmospheric variational data assimilation [1], is an estimate of the atmospheric state in model representation. The aim is to refine this estimate using the best available information, consisting of the latest observations and a forecast model. Adjustments to the model state are made by minimizing a cost function, , which is a measure of the misfit between the current estimate and the incoming information.
Let the current estimate of the state of the atmosphere, 
, be specified as a perturbation, 
from a guess state, 
, such that,
and the background, 
, is,
The cost function in perturbation variables is,
In Eq. (1.3), 
is the background error covariance matrix, 
is the vector of observations and 
is the forward model operator (giving model equivalent of the observations). The error correlation matrix of the observations, 
, is a combination of the error of representativeness and the instrumental error [2].
As it stands, the cost function in model space (ie 
-space) is badly conditioned, and involves directly the use of 
, which has a rank too large to deal with practically. Instead of 
, minimization is done with respect to a control vector, 
, which has none of these problems. If 
is related to 
via [2],
then the preconditioned cost function in control variable space can be written,
Here the background perturbation in 
-space is 
. We have chosen the transformation such that the background error co-variance matrix is absent in the background term (first term of Eq. (1.6)). Thus in 
-space, the background error correlation is the unit matrix [3]. This is an objective of preconditioning [2], and 
is implicit in the transformation, 
.
In order to simplify the notation, it is convenient in the discussion below to write, 
.
How is 
minimized? A descent algorithm makes the desired adjustments, but this requires the gradient of 
with respect to 
. The state 
is a field that we think of as a vector. The gradient of 
thus is also a vector, each component being the partial derivative with respect to its component in 
,
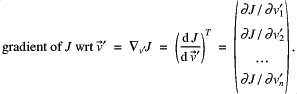
The gradient of 
is expressed fully as,
which follows from differentiating Eq. (1.6) with respect to each element of 
individually, or, by first differentiating with respect to 
, and then using the chain rule [4] to give the gradient in 
-space. The treatment of the background contribution is trivial in 
-space as the gradient of 
is just a difference of vectors. The way that the gradient of 
is found is a three stage process: (i) by applying the forward model (to calculate 
), (ii) differencing with the actual observations and operating with 
as in Eq. (1.8), and (iii) applying the adjoint model to find the gradient. In Eq. (1.8), 
(a matrix) is the linearization of 
(a vector operator). Since in this report, we are dealing with observations, we will focus entirely on 
and its gradient.
The sequence of actions that predict the observations from the model state is the forward model. In the Met Office 3d-Var., the forward model is constructed along the following lines.
(a perturbation state in a transformed space) to the model state, 
(the perturbation state in 'normal' model space) via the 
operator (Eq. (1.4)).
Use interpolation to derive columns of these perturbation quantities at the horizontal positions of the observations, 
.
Add to 
the columns, 
, found beforehand from the guess state (in a similar way to 
). The result is 
.
Operate on the 
columns to give the model version of the observations, 
. These can then be compared with the actual observations, 
.
Steps 2 to 4 are implicit in the 
-operator.
When comparing 
with 
, the following is computed (as part of Eq. (1.8)),
This is the gradient of 
with respect to 
, 
, which is an adjoint vector.
The gradient of 
with respect to 
is found by acting with a string of adjoint operators, which propagate the adjoint state in reverse order to the forward models (the forward model part corresponding to each adjoint are given in brackets below each operator),
In the last line we have highlighted the fact that the operator 
is the adjoint of 
, and the combined operator 
is the adjoint of 
. (Note that in practice, the model field state 
is replaced in the above by a low resolution field -called 
in [2]. We will not be concerned with this here.) In the Met Office Var. scheme, the first three operators, 
, are performed by the core scheme. When adding new observation operators, we need be concerned only with the gradient of 
with respect to 
,
We report here on how we evaluate the forward and adjoint models (up to the stage where the gradient is with respect to 
, as above) for vertical-profile satellite retrievals of ozone, relative humidity and temperature (sections 2, 3 and 4 respectively). We will also describe the treatment of total column ozone (section 5). In the case of profiles, the observed values are specified on a set of vertical pressure levels. We take into account that values of the retrieved profile on these levels do not represent point values, but instead are more like layer averages.
Ozone is specified as a mass mixing ratio, and so the methodology outlined in this section can be applied for any quantity given in this way. Let the pressure of the 
th observation level (on which retrieved ozone, 
, is specified) be 
. These levels are bounded by a set of level boundaries with pressure 
(
). These define the layers that the specified mixing ratios are layer-averaged within). The model level pressures are 
on which there are ozone mixing ratios 
. All of these levels and boundaries are shown schematically in the Fig. below.
The forward model for ozone should mass-weight (within each observation layer) the model's mixing ratio as given on model levels. The result is 
, the model's version of the observations. We assume that the weight of each model level 
contributing to the measured signal within the layer 
is the same (ie that a 'top-hat' weighting function, which is unity within the observation layer and zero elsewhere, is appropriate). This evaluation will involve some interpolation as the observation layer boundaries will not, in general, lie on the model levels.
Given that the mass mixing ratio of ozone between two model pressure levels (found from the arithmetic mean of the mixing ratio at the bounding levels) is 
, then the total amount of ozone in this model layer per unit horizontal area is,
where 
is the density, and 
is the height thickness of the layer. We assume that the shallow atmosphere approximation is valid as we will take the horizontal area of the column to be constant with height. The height thickness, 
, can be found from the pressure thickness, 
, under the hydrostatic approximation,
This information allows us to write a 'layer averaging' operator 
(see below). As this operator is linear, its adjoint, 
follows in a straightforward manner (also see below).
The information required by the layer averaging operator includes: 
(the number of model levels), 
(the number of observation layers), 
(the observation layer boundary pressures - there are 
of these), 
(the model level pressures) and 
(the model's mass mixing ratio of the trace substance that we are interested in - in this case ozone). The output is 
(the observation layer averaged mixing ratio). 
is the model version of 
(the observed value).
It is convenient to describe also an auxiliary structure 
. This is an index pertaining to observation layer boundary 
and references the first model level immediately below it. To use the schematic in the above Fig. as an example, it can be seen that 
indicating that model level 5 is immediately below observation layer boundary 2.
The algorithm for 
is now described.
For each observation layer |
Importantly, in the above, the gradient 
is calculated on model levels as a forward difference, 
.
Since the forward model is linear, it is straightforward (albeit tedious and time consuming) to give the algorithm for the adjoint. In the case of the layer average operator, the adjoint takes us from the gradient (of 
) with respect to the layer averages, to the gradient with respect to the model columns of mixing ratio (see section 1),
Note that since 
depends on model variables in other ways, we have partial derivatives. Equation (2.3) is nothing more than the generalized chain rule [4]. In this Eq., the values of 
have been assembled into the model vector 
(akin to a subset of 
introduced in section 1 of this report - as in Eq. (1.13)), and the layer average quantities 
into the vector 
(akin to a subset of 
). In order to construct the adjoint, it is useful to first imagine the forward operator for 
in differential form written as a linear combination of the model values, 
,
The coefficients 
, which can be derived by considering the forward algorithm, form an 
matrix and the above left-hand Eq. can be written in matrix form, 
. With the coefficients known, the adjoint can be constructed. From first principles, this is done via the chain rule component-by-component,
In matrix form this is (as in Eq. (2.3)),
A simple strategy to construct the adjoint is the following. First note that a matrix element, 
, appearing in the forward model transfers information from model level 
to observation layer 
, as 
. For each such element, the adjoint spreads information the other way such that 
(of course the transpose instruction is absent in the last Eq. as it is not in matrix form). Repeating this last action over all non-zero matrix elements achieves the adjoint operation.
The adjoint algorithm follows from this procedure. Note first that when writing the forward model as a linear combination, one should expand the derivatives 
that are present in the forward model algorithm. This yields more terms than is first apparent. In the following, each adjoint contribution is accompanied (in red curly brackets) by the forward contribution on which it is based.
For each observation layer |
In this algorithm, 
is the derivative of 
with respect to the 
th component of model ozone. Similarly, is the derivative of
with respect to the 
th component of the model-observation (layer averaged) ozone.
Relative humidity is not a mixing ratio, and so it is meaningless to layer average this quantity. Instead, we must convert the model values to something that does resemble a mixing ratio.
The forward model is comprised of the algorithm outlined in the following list. Note that the model variables available are 
and 
(potential temperature and relative humidity respectively, each on model level 
). These are actually contained within the vector 
. The model version of the relative humidity observations are, for observation layer 
, 
, and form part of the vector 
. Here is the forward model:
to temperature, 
by multiplying by the exner pressure,
is the thermodynamic constant of 0.286, and 
is the reference pressure of 100 hPa).
2. Calculate the saturation water vapour partial pressure, 
. The partial pressure is a function of temperature only and in the Met Office, values are found by reference to look-up tables (the derivative, 
, which is required for the adjoint calculation later, can also be returned at this stage).
3. From 
, calculate the saturated specific humidity, 
,
is the ratio of molecular weights of water vapour to dry air, 
).
4. Compute the actual specific humidity,
5. The specific humidities from step 4 resemble mixing ratios and so we can apply the layer averaging as for ozone (the 
operator in section 2). The results are on observation layers, 
and 
.
6. Convert the layer-averaged specific humidities back to partial pressures,
Note that there are differences in (i) the definition of relative humidity used in the calculation on model levels (step 4) and in observation layers (step 7) and (ii) the relationship between specific humidity and water vapour partial pressure in the same context (steps 3 and 6 respectively). These reflect the different definitions/approximations used within the Met Office Var. scheme and within the observation processing stages of the assimilation.
Since the calculation of layer average relative humidity is a complicated multi-stage process, we show here the principle of the adjoint calculation. The forward process is non-linear and so it is helpful to first show the corresponding linearized model (or perturbation forecast model). This is most simply done via the chain rule, noting that an increment in 
depends ultimately on increments of 
and 
,
This expression has been derived systematically from the forward model, starting at step 7 and working backwards and the sum is over model levels. We prefer to refactorize the expression with the 
dependencies together,
which will make the adjoint more straightforward. We note the following formulae for some of the partial derivatives,
Putting these terms into the series yields,
which we rewrite once more exactly as (using Eqs. (3.4) to (3.6)),
In vector and matrix notation, the above expression is written as (
),
where 
, 
and 
are diagonal operators in observation layer space, 
, 
and 
are diagonal operators in model level space, and 
is the non-diagonal layer averaging operator. This transforms from model level to observational layer space, and implies the sum over levels. The diagonal operators are defined as the following,
Once written in this way, it is straightforward to write the adjoint expression, which propagates gradient information from observation to model variables,
Note that diagonal operators are self adjoint, and so the transpose superscript has been omitted for these.
Special relations apply to the assimilation of temperature data. We have at our disposal the hydrostatic approximation, 
, and the Eq. of state, 
. These can be combined to give an expression for the layer-mean temperature,
where 
is the layer thickness in height, 
is the layer thickness in log-pressure, 
is the specific heat capacity of air at constant pressure, and 
is the thermodynamic constant of 0.286. This is the "hypsometric" relation.
Routines to perform the layer average in temperature pre-exist in the Met Office Var. scheme and so the forward model routine and its adjoint will not be documented further here.
The forward and adjoint models for total column ozone measurements are a subset of the layer averaging operators (section 2) in the limit of a single layer spanning the entire thickness of the model atmosphere. The implementation described here however is separate.
The calculation of total column ozone has two contributions. The first is the bulk contribution from all model levels and the second is from the surface layer. Surface ozone is not a model variable and so we extrapolate linearly (in log-pressure) to the surface.
|
|
In this algorithm, 
is the surface pressure (this is known as it is a model variable). For total column ozone, the surface contribution to the total column will probably be negligible, but it is left in the forward model algorithm to make the code extendable to other species that may be present here at higher concentrations.
The forward model is linear and is, in effect, a 
matrix. The adjoint is a 
matrix that propagates the gradient information from that with respect to a single model measurement to that with respect to a model ozone profile. As always it is helpful to derive the adjoint model from the perturbation forecast model found beforehand. For this reason each line of the the adjoint algorithm (below) is accompanied by its corresponding line in the perturbation forecast model (inside red curly brackets).
|
The derivative notation is as the adjoint algorithm for layer mean quantities, additionally with 
.
We make a special note about total column quantities. Total column 'observations' are not direct measurements, but are highly processed from satellite measurements. Despite their name, they are not exactly the total column amounts of the substance in question (e.g. ozone), but are a weighted total column (weighted with some averaging kernel) [5]. Although this is strictly the case, we assume in the above algorithm that the averaging kernel is unity.
| Name | Section | Module directory | Author |
| Var_LayerAv | 2 | VarMod_MLS | DARC (RNB) |
| Var_LayerAv_Adj | 2 | VarMod_MLS | DARC (RNB) |
| Var_RHLayerAv | 3 | VarMod_MLS | DARC (RNB) |
| Var_RHLayerAv_Adj | 3 | VarMod_MLS | DARC (RNB) |
| Gen_LayerTemperature | 4 | GenMod_Utilities | Met Office |
| Gen_LayerTemperature_Adj | 4 | GenMod_Utilities | Met Office |
| Var_CalcModelTCO3 | 5 | VarMod_GOME | DARC (RNB) |
| Var_CalcModelTCO3_Adj | 5 | VarMod_GOME | DARC (RNB) |
[2] A.C. Lorenc, S.P. Ballard, R.S. Bell, N.B. Ingleby, P.L.F. Andrews, D.M. Barker, J.R. Bray, A.M. Clayton, T. Dalby, D. Li, T.J. Payne, F.W. Saunders, The Met Office 3-dimensional variational data assimilation scheme, Q.J.R. Meteorol. Soc. 126, pp. 2991-3012 (2000).
[3] D.F. Parrish, J.C. Derber, The National Meteorological Center's spectral statistical interpolation analysis system, Mon. Wea. Rev. 120, pp. 1747-1763 (1992).
[4] R.N. Bannister, Applications of the chain rule, http://www.met.rdg.ac.uk/~ross/Documents/Chain.html (2001).
[5] C.D. Rodgers, Inverse methods for atmospheric sounding: theory and practice, Series on atmospheric, oceanic and planetary physics, Vol. 2, World Scientific (2000).
(the layer is bounded by pressures 
and 
):
If 
then
(there is at least one model level in this observation layer)
First sum over any complete model layers
If 
then
(there is at least one model layer within this observation layer),
.
end if-block
Include the contribution from the 'ends' (incomplete model layers)
'Lower' contribution: 
'Upper' contribution: 
Layer average: 
else
(there are no model levels in this observation layer)
end if-block
(the layer is bounded by pressures 
and 
):
If 
then
(there is at least one model level in this observation layer)
First deal with any complete model layers
If 
then
For each integer (
) between 
and 
Let 
{
}
{
}
end loop
end if-block
Include the contribution from the 'ends' (incomplete model layers)
The 'lower' contribution:
Let 
, 
, 
{
}
{
}
The 'upper' contribution:
Let 
, 
, 
{
}
{
}
else
(there are no model levels in this observation layer)
Let 
{
}
{
}
end if-block
) between 3 and 
{
}
end loop
Contribution of the top ozone level
{
}
Contribution of ozone level 2
{
}
Contribution of ozone level 1
{
}