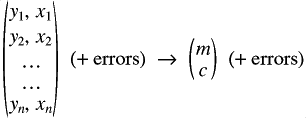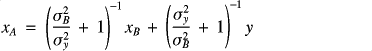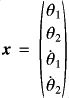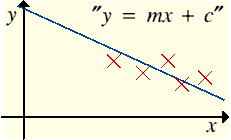
What does an inverse model do?

'Forward' model

Model parameters: and

'Inverse' model

Examples of inverse modelling ...

... and any situation in where:

• observations are noisy,
• observations are incomplete and irregular,
• parameters cannot be measured directly.

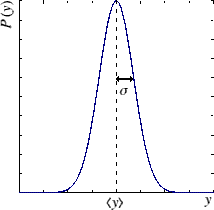
Parameter Estimation by Maximum Likelihood (Method of Least Squares)

Gaussian error characteristics (one variable)

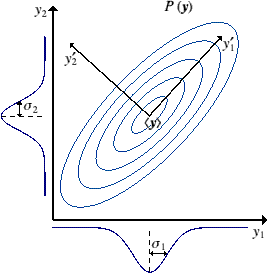
(two or more variables)

Ingredients (for an inversion)

1. Observations
2. A-priori (background)
3. Constraints ...

The forward model (strong constraint)

How will 1,2,3 combine to give the most likely set of parameters?

Bayes' Theorem:

Maximum likelihood = minimum penalty

Notes on the cost function

For unknown parameters in , and observations in ,

Why "least squares"?

Eg. if is non-linear ...

Methods of Inverting

1. Cressman Analysis

Cheap. Easy to implement. A-priori in data-poor regions. No account of errors. Not dynamically consistent. Direct observations only. No forward model used.

2. Best Linear Unbiased Estimator (BLUE)

3. Variational Analysis (4d-Var)

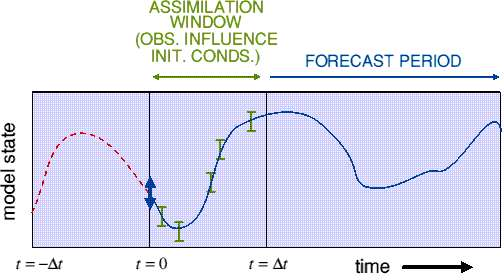
• Account taken of errors.
• Can use indirect obs. and non-linear operators.
• Suitable for large Nos. of degrees of freedom.
• 4d-Var is dynamically consistent.
• A-priori in data poor regions.
• Difficult to know .
• Expensive.
• Difficult to implement and use.
• Needs preconditioning.

4. Kalman filter

• Account taken of errors.
• Can use indirect obs.
• A-priori in data poor regions.
• Evolves in time.
• Difficult to use with non-linear operators.
• Very expensive.
• Difficult to use practically.

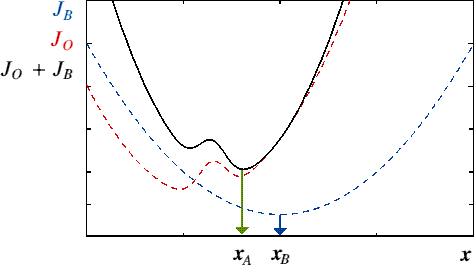
Example with BLUE

1 unknown parameter, 1 observation, 1 initial estimate

	Value	Uncertainty
Prior estimate
Observation
Forward model		-------

BLUE formulae:

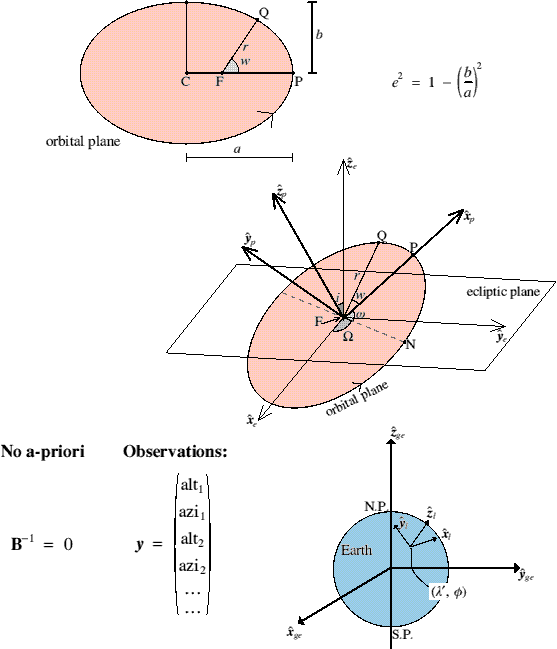
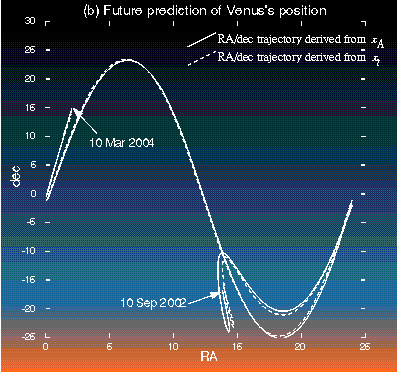
Example with BLUE

(Astronomy - Inverting Kepler's Equation)

Want to determine orbital parameters:

Physics of the forward model:

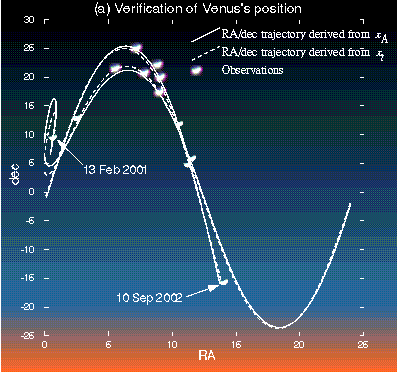
Inversion results

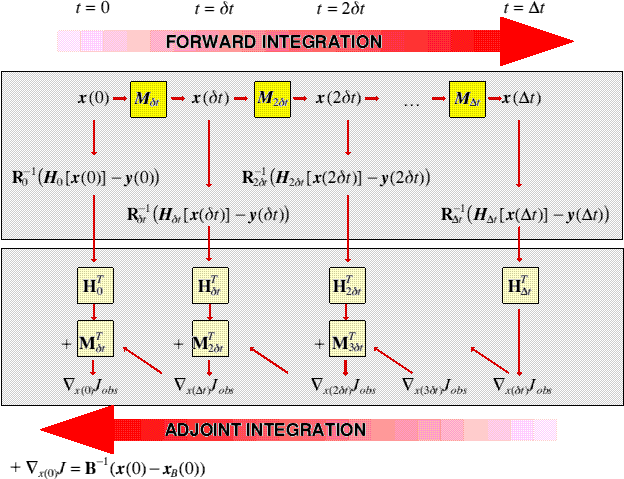
4-Dimensional Variational Data Assimilation

Leith, 1993:

... the atmosphere "is a chaotic system in which errors introduced into the system can grow with time ... As a consequence, data assimilation is a struggle between chaotic destruction of knowledge and its restoration by new observations."

Schematic limb radiance operator

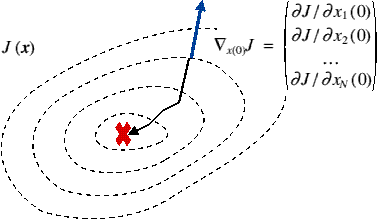
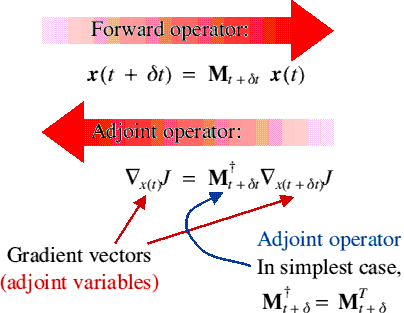
Adjoint Variables and Adjoint Operators

The adjoint of an operator propagates the adjoint variables in the reverse sense

(this is just the chain rule generalised to many variables)

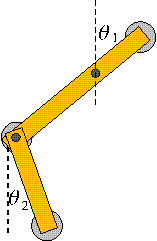
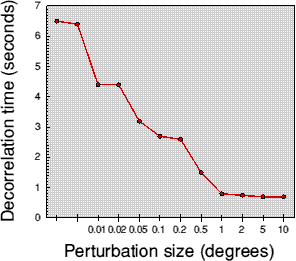
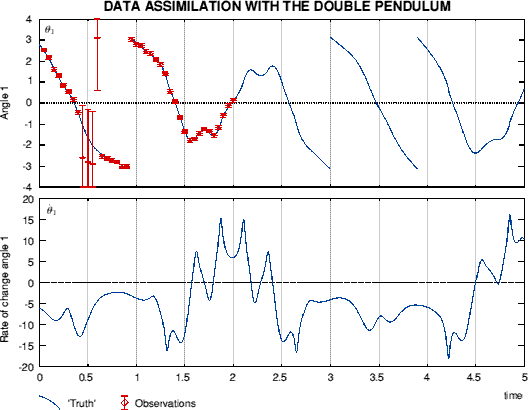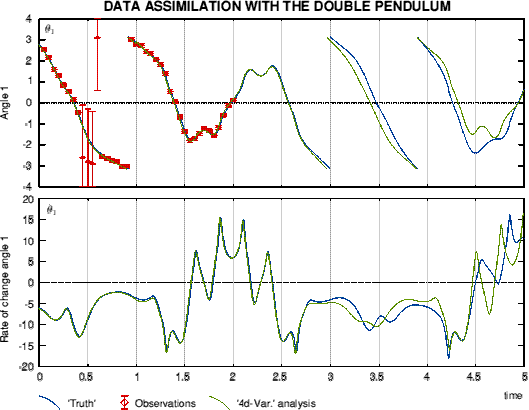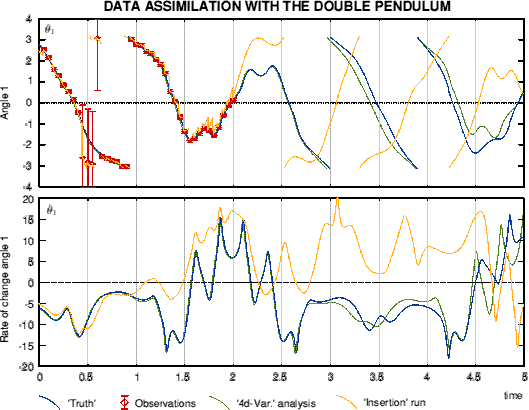
Example of '4d'-Var. with a simple chaotic system

The double pendulum

Other GFD applications

Sources/sinks determination

Forward model (tracer transport Eq.):

What are the sources/sinks, given observations of ?

Cost function:

Gradient w.r.t. :

Other bonuses of doing inverse modelling / DA

• Model performance
• Observation quality

Some difficulties with inverse modelling / DA

• Non-linearity (errors, parametrisations)
• Model budget disruption by obs.
• The 'initialization problem'
• Treatment of model error
• Null space
• Error characterization, esp. multivariate
• Artefacts from unrealistic

Summary

Inverse methods:

• are an integral part of science
• infer information about model parameters using:
  • noisy, irregular, and indirect measurements
  • how the system behaves
• require expertise in:
  • forward modelling
  • inverse techniques
  • dealing with large volumes of information
• make use of a number of methods and assumptions, for DA:
  • Gaussian error characteristics
  • method of least squares
  • B.L.U.E. / 3d/4d Var. / Kalman filter
• can help assess:
  • model performance
  • observation quality
• becomes difficult esp:
  • non-linear models
  • large No. of degrees of freedom
  • multivariate
• suffer potential problems:
  • representing B
  • artefacts
  • null space