Polarisation algorithms to correct for attenuation at C-band

Chun-Lei Liu and Anthony J. Illingworth

The problem

Attenuation is a severe problem at C-band
C-band used operationally in Europe and Japan
Gate-by-gate correction of Z is notoriously unstable
Attenuation is not uniquely related to differential phase shift

Simulations by Bringi et al (1990) suggested attuation is related to differential phase shift, but they did not consider Values of median diameter D₀ above 2.5mm (Z_DR>3dB). Most attenuation events have higher Z_DR (Smyth and Illingworth, QJ, 1998 p2398).

Non-polarisation technique solution

UK Met. Office currently use empirical 2-way correction at C-band (Gunn and East 1954):

A = 0.0044 R^1.17 dB/km at 18°C (1)
It is based on exponential drop spectra with the drop shape of sphere. Gate-by-gate correction can blow up, so the correction is capped at 3 dB.
New rain size-spectrum analysis: raindrop spectra are best represented by normalised gamma functions

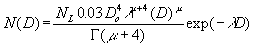     (2)

where D₀ is the diameter that splits the volume of water in two equal parts. Fitting to spectra by forcing the third, fourth and sixth moments to equal the appropriately weighted integral of the gamma function show that N_L is close to 8000 m³mm^-1 (Marshall-Palmer value) and mu is about five. this leads to a relationship of the form:

A_v = 0.00258 R^1.23 dB/km at 0°C      (3a)
A_v = 0.00124 R^1.31 dB/km at 20°C    (3b)

This is about 50% of the value predicted by Equation 1 (Gunn and East); e.g. for 100mm/hr, the Gunn and East formula predicts 1 dB/km wherease the new gamma functions predict 0.5 dB/km.

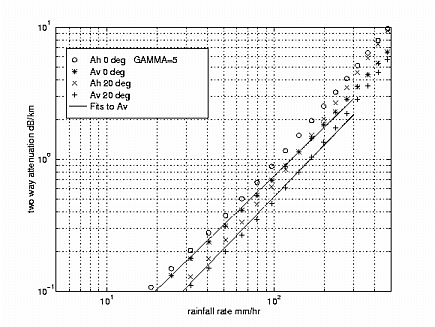
Predicted C-band attenuation for horizontal and vertical polarisation at 0°C and 20°C for a normalised gamma function with mu=5 and N_L = 8000 m^-3mm^-1.

Conclusion: recommend (3b) used operationally in the UK, not (1)

Polarisation technique solution

At S-band, simulations by Bringi et al (1990), in which D₀ was limited to 2.5 mm, suggested the attenuation could be derived from differential phase shift (K_DP). This leads to
Total attenuation A_h = 0.016 K_DP dB/°
Differential attenuation A_h-A_v = 0.00367 K_DP dB/°
but D₀ = 2.5 mm is a Z_DR of only 3 dB; most attenuation events have higher Z_DR values (i.e. large raindrops)
If we extend simulations up to D₀ = 3.5 mm we find the unique relationship breaks down and we can't derive attenuation from differential phase shift (K_DP).
Observations of differential attenuation and differential phase shift confirm there is no simple relationship between the two. A plot of observed negative Z_DR against total differential phase suggests
- Attenuation higher than Bringi et al.
- Highest values of all when Z_DR > 5 dB (bold points)
- Ryzhkov and Zrnic (1994) also found differential attenuation higher than Bringi et al. and invoked half melted ice cores, but this can be explained simply by high-Z_DR rain.

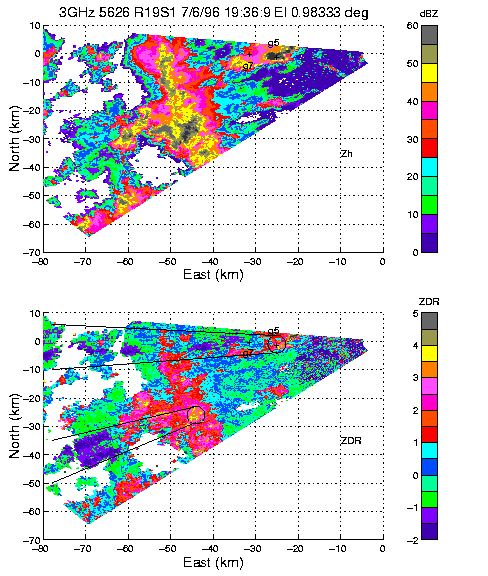
Example of negative Z_DR at S-band behind intense rain cells (high Z and Z_DR). Gauge 5 was recording a rain rate of 267 mm/hr.

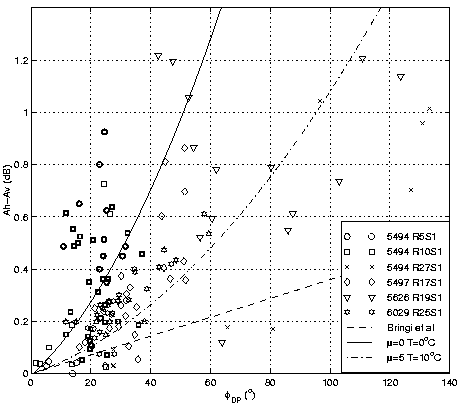
Observed values of total differential phase shift, phi_DP. Total differential attenuation, A_h-A_v, observed behind intense echoes with the s-band chilbolton radar. Bold points correspond to rays with Z_DR above 5 dB

Simple solution at C-band

At C-band, it turns out that differential attenuation is linearly related to total attenuation. so we can estimate total attenuation from the negative Z_DR behind the heavy rain.
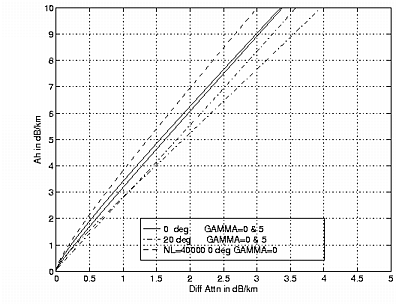
Predicted variation of A_h versus A_h-A_v at C-band for N_L = 8000 m^-3mm^-1 at 0°C and 20°C for mu = 0 and 5. The dashed line is for N_L = 40000 m^-3mm^-1.
The problem with using K_DP to correct for attenuation is that K_DP depends on the real part of the forward scatter amplitude, and attenuation to the imaginary part; these have different behaviour with size and temperature.

However, differential and total attenuation both depend on the imaginary part of the scatter amplitude, so

Recommend use of negative ZDR behind heavy rain to estimate total attenuation.
Would work for UKMO C-band radars if radars had dual polarisation.