1. Introduction
Waves occur in almost all branches of science. The basic concepts discussed in this introductory package may be applied to all waves including the three shown below:
Waves are typically disturbances in some medium: they include electro-magnetic waves (such as light or radio waves); movements of gas molecules (sound waves) and movements in solids (seismic waves).
An understanding of waves is crucial for all these phenomena and much more.
2. Amplitude, Wavelength, Frequency and Period
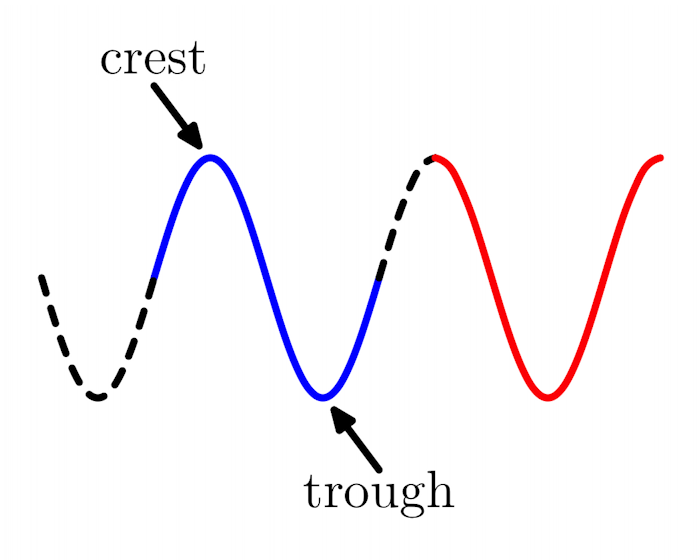
Consider the waves shown on the right, in which the solid red and blue parts are both a full cycle. For the blue cycle the wave oscillates up from its central value to a crest, then down through a trough and back up to its central value. The red cycle passes down from a crest to a trough and back up again to its initial peak value. Let us now consider how to parameterise the shape of a wave. |
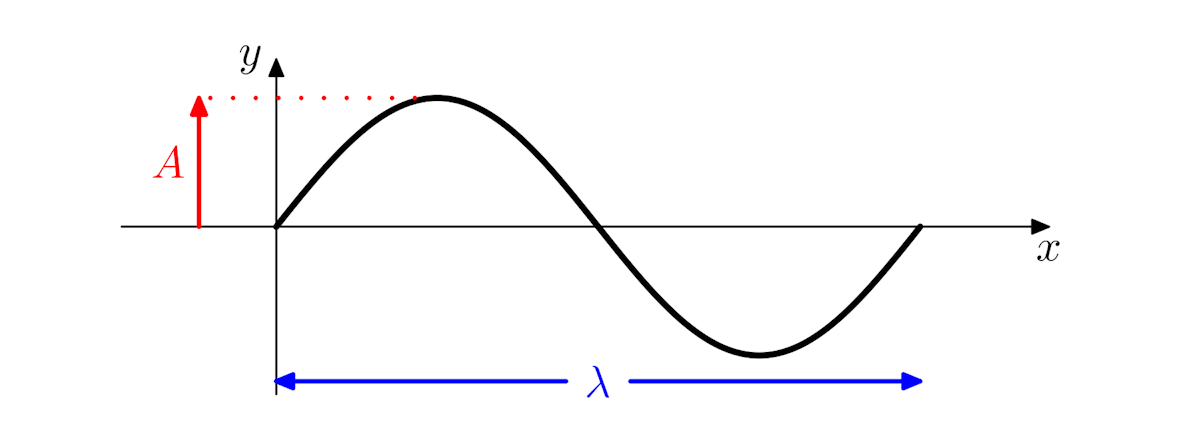
The figure on the left shows a snapshot of a wave at a fixed time. The maximum disturbance, A, from the central value is the amplitude of the wave. The length of a full cycle, λ, is the wavelength. |
|
 |
Example 1: Here, this wave has an amplitude of 3mm and a wavelength of 4cm (measured, say, from crest to crest or trough to trough).
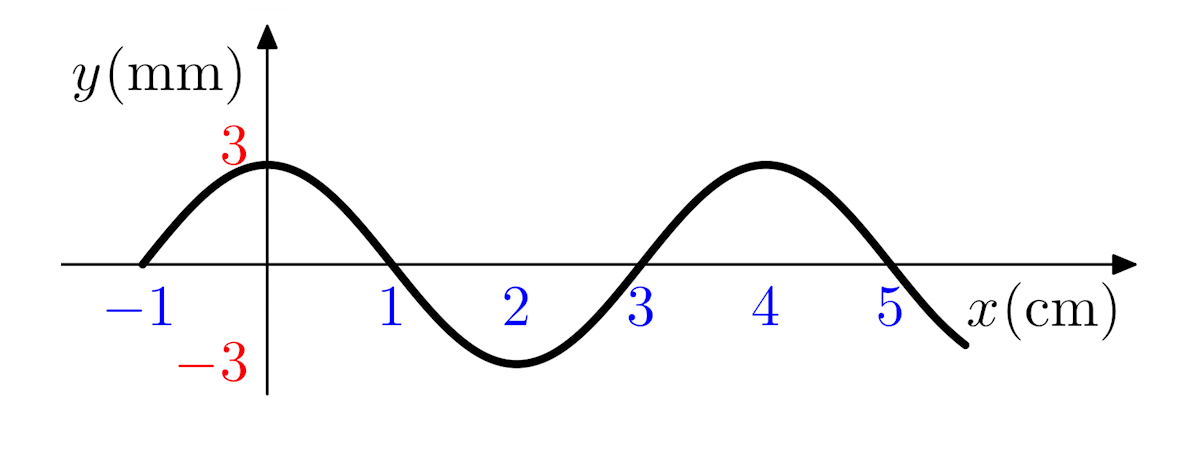
Exercise 1: These exercises refer to the three waves shown below:
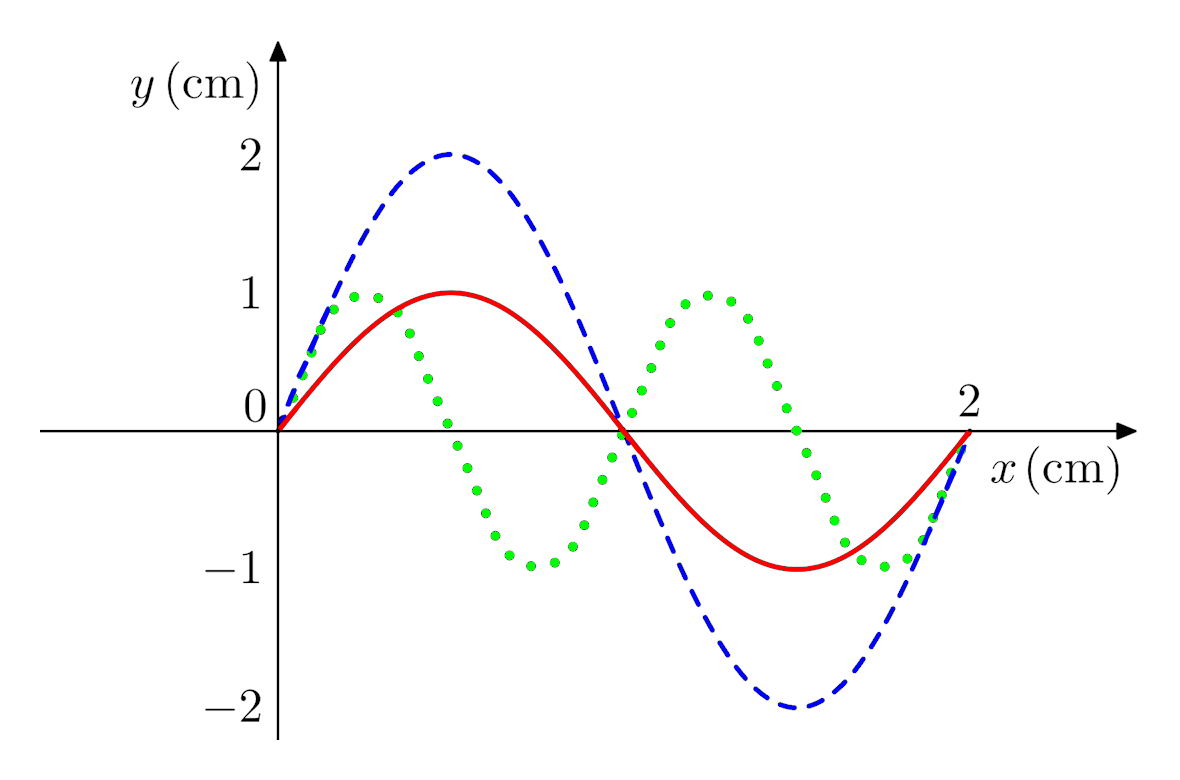
Solution: The figure shows that the maximum positive disturbance of the solid (red) wave from the x-axis is 1cm, therefore the amplitude A = 1cm
Solution: From the figure we see that the solid (red) wave has a full cycle between the two points at x = 0cm and x = 2cm. Therefore, its wavelength λ = 2cm
Solution: Comparing the cycles of the dashed (blue) and dotted (green) waves shown in the figure, we see that the dashed wave cycle is twice as long as the dotted one. The wavelengths λdashed and λdotted obey the relation:
Solution: From the figure, the full cycles of the dashed (blue) and solid (red) waves are the same, therefore the wavelengths λdashed and λ are equal:
Note however, that the corresponding amplitudes are different; the amplitude Asolid is half of Adashed:
Click on questions to reveal solutions
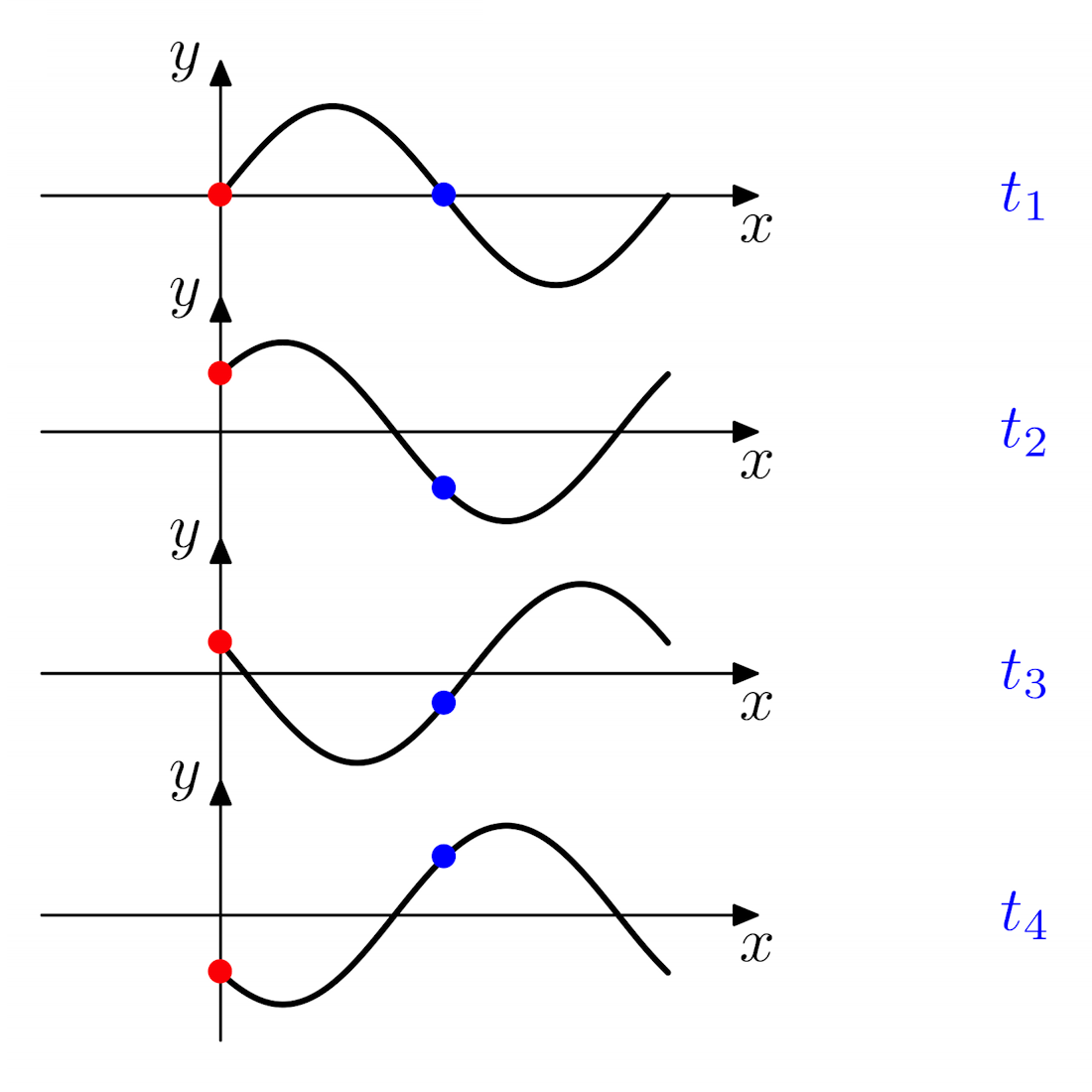
In the figure below, a wave is plotted at successive moments in time. This shows how the wave oscillates at a fixed position (for example the red or blue points).
|
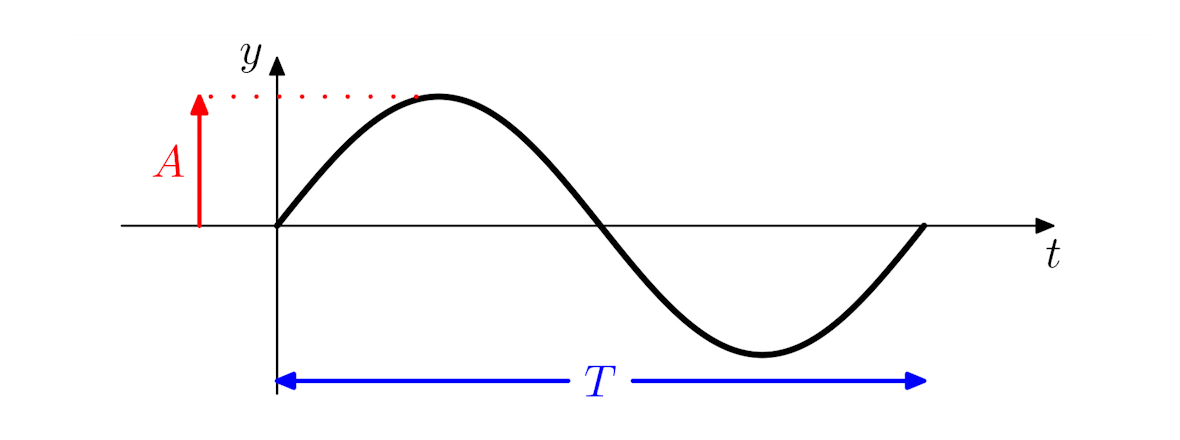
In the figure above, a wave at a fixed position is plotted against time. Again, A is the amplitude of the wave. The time taken for a full cycle T is the period of the wave.
ν = 1 secondtime for a full cycle = 1T
This also implies:
T = 1ν
Frequency units: 1 cycle per second is also called 1 Hertz (1Hz). |
Example: If the frequency of a wave is 4Hz, what is its period?
Solution:
This result shows that four times the period is equal to one second, i.e., the frequency is 4 cycles per second.
Frequency, wavelength and the speed of a moving wave are related as follows: during the period of a full cycle, T, the wave travels a wavelength, λ, so its speed, v, is:
Since ν = 1/T this can be rewritten as:
Thus, for a given speed v, high frequencies correspond to short wavelengths, whilst low frequencies have long wavelengths.
Example 3: If a seismic wave is measured to have a wavelength of 15m and frequency 100Hz we can find its speed as follows:
| v | = | νλ |
| = | 100 × 15 = 1,500m s−1 |
Exercise 2:
Solution: Given the frequency ν = 1,700Hz, the wavelength λ can be found from the relation:
- where v is the speed of sound in air. Using the known experimental value of the speed of sound in air v = 340m s−1, we have:
| 340 | = | 1.700 × λ |
| ∴ λ | = | 340m s−1 1,700Hz |
| = | 2 10m = 0.2m |
Solution: Consider the same sound wave with frequency ν = 1,700Hz but now in a metal where its speed is much higher, v = 5,100m s−1. From this data and the equation:
| 5,100 | = | 1.700 × λ |
| ∴ λ | = | 5,100m s−1 1,700Hz |
| = | 51 17m = 3m |
Solution: Consider the radio waves with frequencies ν = 103.4MHz and ν = 855kHz, propagating with the speed of light, which is approximately c = 3 × 108m s−1. The corresponding wavelengths λ can be found from:
For the FM waves, ν = 103.4MHz, so:
| 3 × 108 | = | 103.4 × 106 × λ |
| ∴ λ | = | 3 × 108m s−1 103.4 × 106Hz |
| = | 3 103.4 × 102m = 0.3m |
while for the AM band with frequency ν = 855kHz we have:
| 3 × 108 | = | 103.4 × 106 × λ |
| ∴ λ | = | 3 × 108m s−1 855 × 103Hz |
| = | 3 855 × 103m = 300m |
Note the relations 1 MHz = 106Hz and 1kHz = 103Hz.
Click on questions to reveal solutions
Quiz 1: The audible frequency range lies between 20Hz and 20,000Hz (20kHz). What is the maximum period of an audible wave?
Explanation: Frequency ν and period T of the wave are inversely related:
Therefore, if the audible frequency range is:
then the period lies between (note the reversal of the inequalities!)
So, the maximum period of an audible wave is:
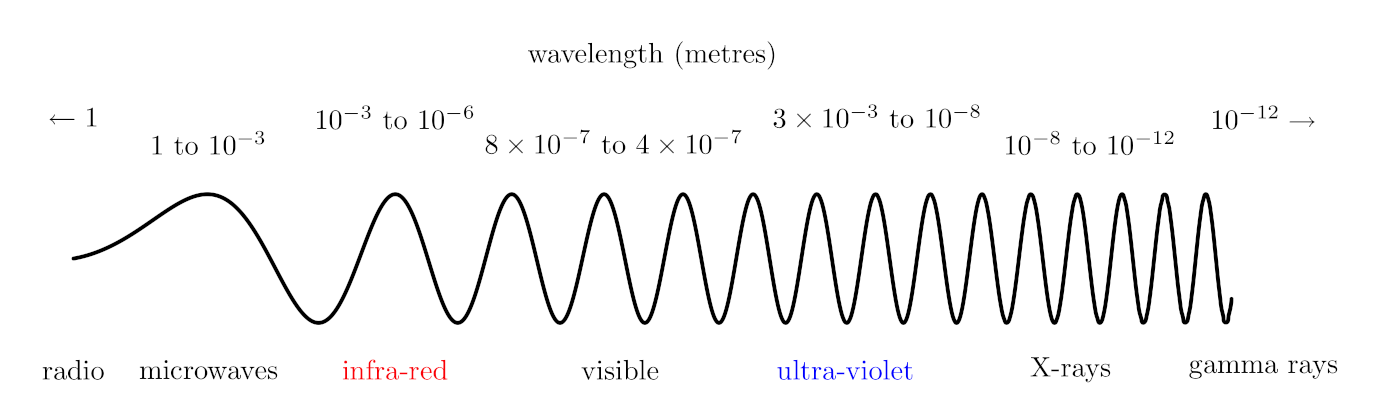
Exercise 3: These questions refer to the electromagnetic spectrum which is shown (not to scale) below. (Recall that the speed of light c = 3 × 108m s−1):
Solution: The frequency of an electromagnetic wave is given by:
and noting that the range of the wavelength λ of the microwave radiation is:
the highest frequency of a microwave radiation is:
Solution: The range of X-ray wavelengths is:
From:
we can calculate the lowest X-ray frequency:
Solution: From:
and noting that the wavelength interval of infra-red radiation is:
we find the that band of frequencies of infra-red radiation is:
Solution: The visible light wavelengths interval is:
The formula for the electromagnetic wave period T = 1ν in terms of the speed of light and its wavelength λ is:
Thus, the lowest period of visible light is:
Click on questions to reveal solutions
3. Interference and Phase
Example 4: Here are examples of adding the blue dotted and dashed waves. The red solid lines are the results of the interference:
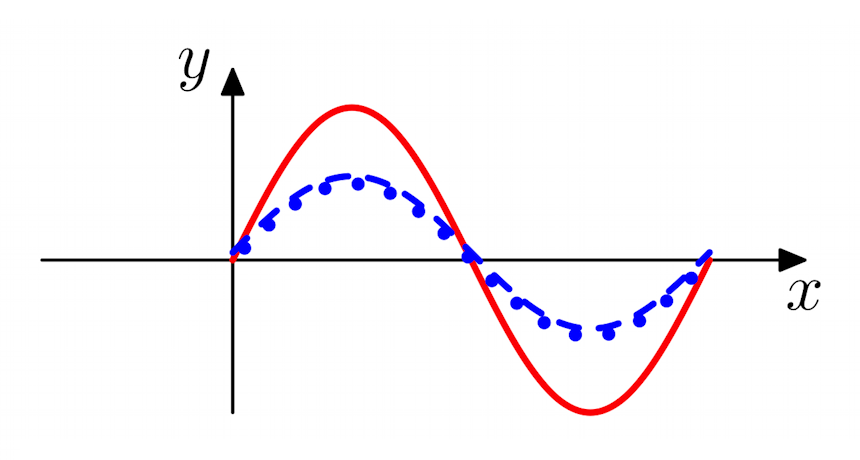
Reinforcement, or constructive interference, occurs when crests from the one wave arrive at the same point as the crests from the other wave. (They are said to be superimposed.) |
Cancellation, called destructive interference, takes place when crests from one wave are superimposed on troughs from the other wave. |
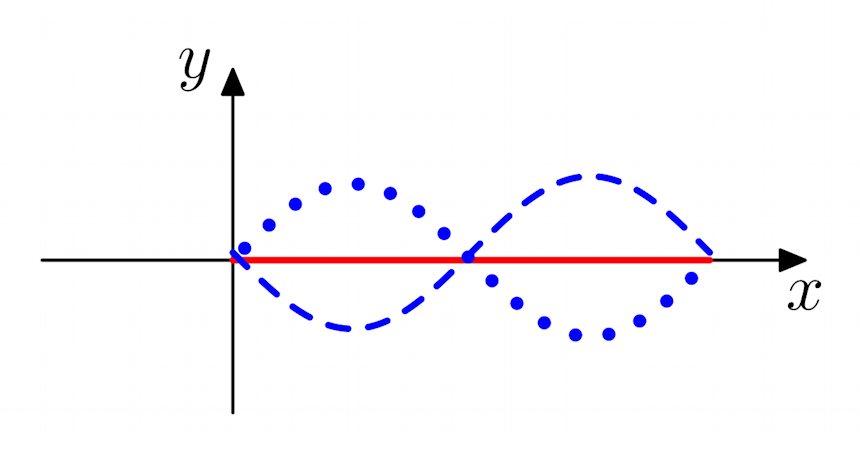
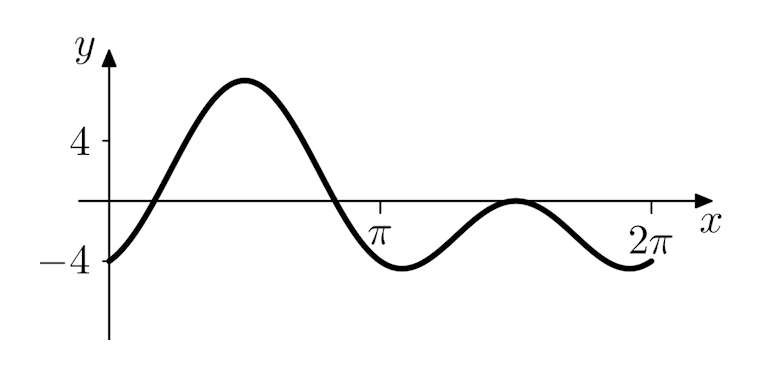
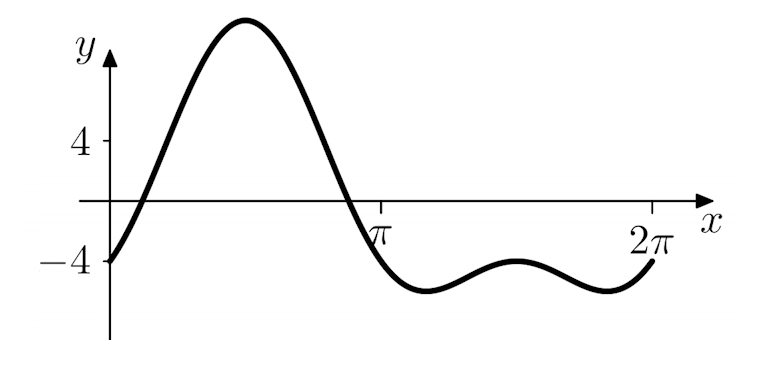
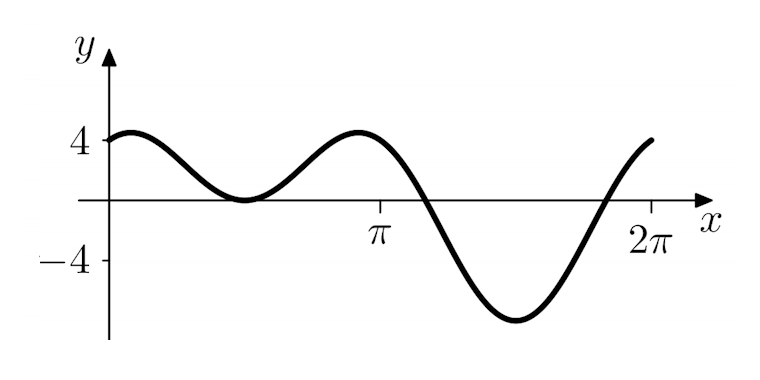
Quiz 2: Select from the figures shown below the result of superimposing these two waves:
 (a) Wrong - please try again! (a) Wrong - please try again!
|
 (b) Wrong - please try again! (b) Wrong - please try again!
|
|
 (c) Wrong - please try again! (c) Wrong - please try again!
|
 (d) Correct - well done! (d) Correct - well done!
|
Explanation: To select the correct result of superposing the two given waves, consider the interference at different points along the x-axis. From the main figure at point x = 0 , the disturbance from the x-axis of the red wave is y = 4, whilst the disturbance of the blue wave is y = 0. The resulting wave disturbance ysup at this point is thus:
Figures (b) and (c) are therefore incorrect.
Similarly, we see that constructive interference occurs at x = 3π ⁄ 2:
Comparing the waves of the remaining figures (a) and (d), we see that only figure (d) is correct.
The phase difference, Δφ between two points on a wave is the fraction of a complete cycle between the points. It is measured in degrees (360° being a full cycle) or radians (one cycle is 2π radians).
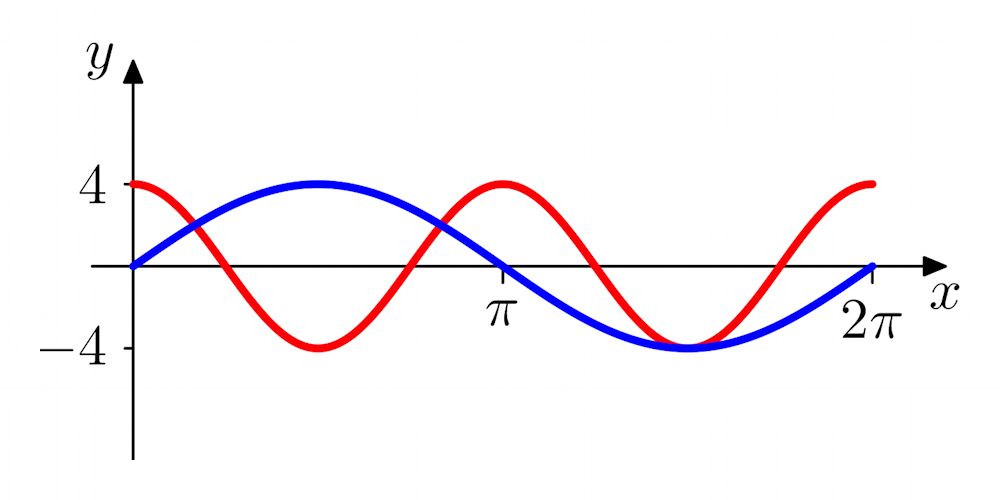
Example 5: Consider the wave shown below:
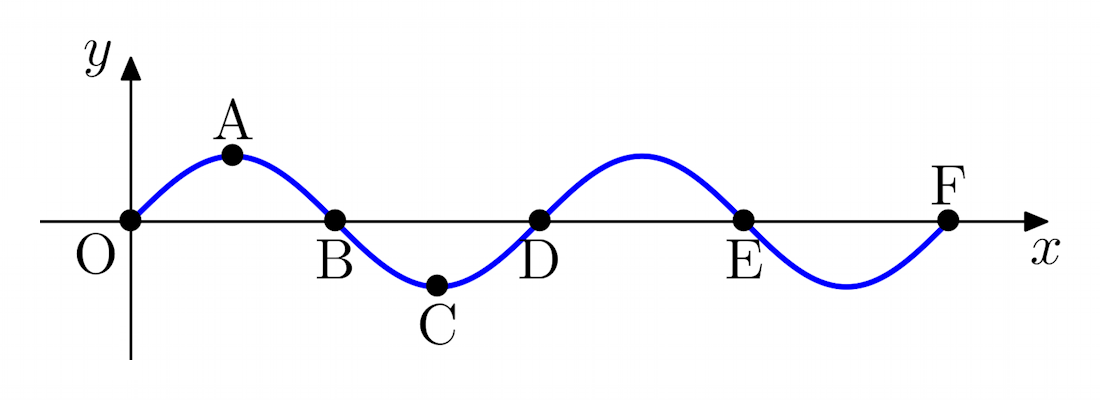
The phase differences at the given points relative to the point O are:
| Point | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Degrees | 90° | 180° | 270° | 360° | 180° | 360° |
| Radians | π ⁄ 2 | π | 3π ⁄ 2; | 2π | π | 2π |
The points O, D and F are all in phase with each other. B is out of phase with O as the wave is then moving in the opposed direction. The phase difference between B and C is π ⁄ 2 or 90°.
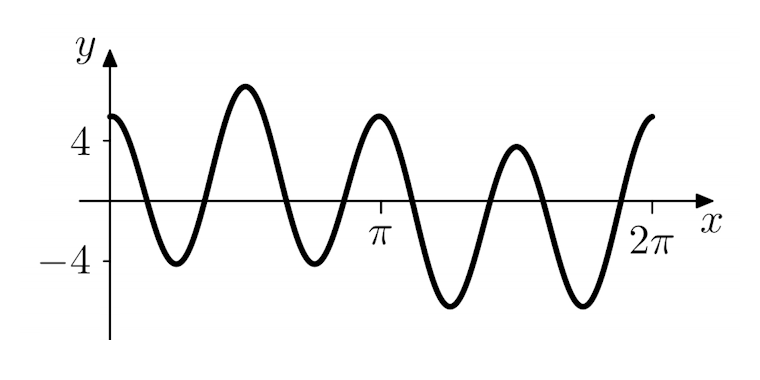
Exercise 4: These exercises refer to the points marked on the wave below:
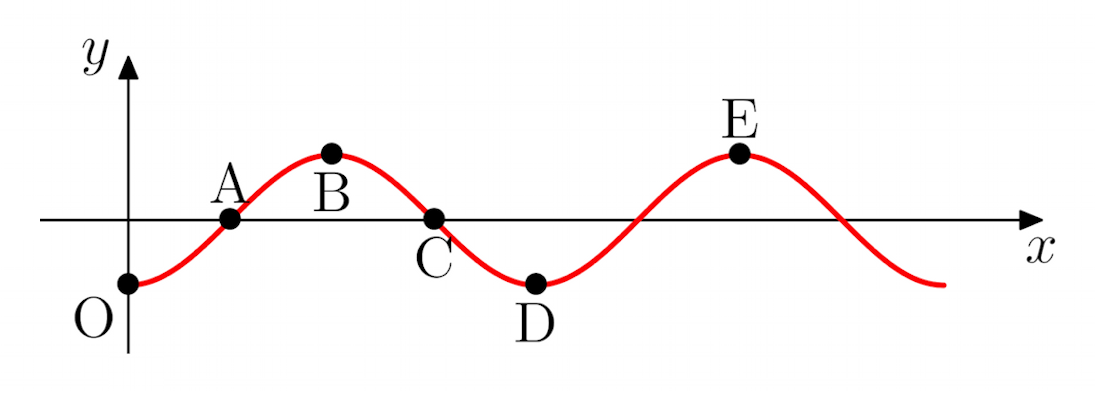
Solution: The point O lags the point A by a quarter of a full cycle and therefore the phase difference between these points is:
Solution: From the figure, we see that the point O is in phase with point D:
Solution: From the figure we see that the point C leads the point O by three quarters of a cycle. Therefore the phase difference between these points is:
Solution: The figure shows that the point A lags the point C by half of the whole cycle. So, the phase difference between the points A and C is:
Solution: From the figure we see that the point B lags the point C by a quarter of the whole cycle, whilst the point D leads the point C a quarter cycle. Therefore, the phase difference between the points B and D is:
Click on questions to reveal solutions
4. Quiz on Waves
For each of the following questions, select one answer from the options given:
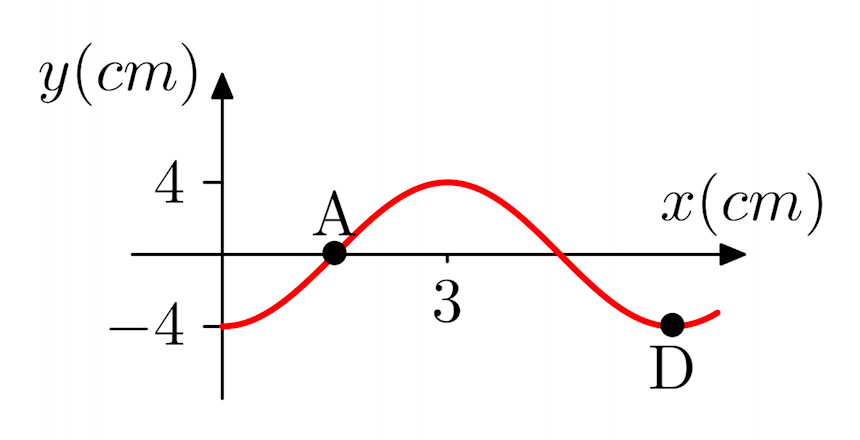
1.What is the phase difference (in radians) between A and D in the figure on the right?
(a)π ⁄ 2
(b)3 π ⁄ 2
(c)π
(d)3 π ⁄ 4
2.What is the amplitude of the wave in the figure on the right?
(a)8cm
(b)3cm
(c)4cm
(d)1.5cm
|
 |