1. Theory
The purpose of this tutorial is to practice working out the vector product of two vectors.
It is called the 'vector product' because the result is a 'vector', i.e. a quantity with both magnitude and direction.
| NOTE: Throughout this tutorial we use the notation a to denote a vector quantity. However, there
are alternative notations, such as a, which are used in the PPLATO Interactive Mathematics modules (see Notation Section). |
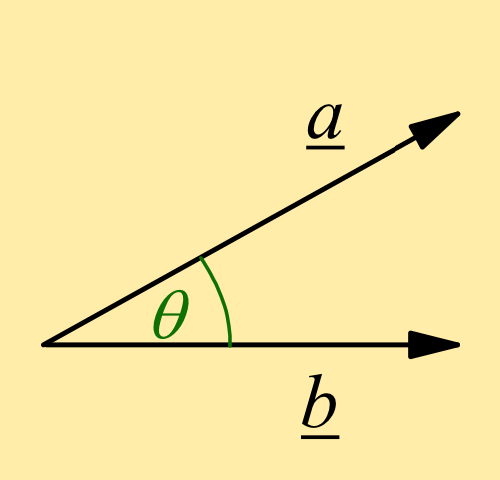
The magnitude of the vector product of a and b
a×b = a bsin θ
where θ is the angle
between a and b
|
 |
|
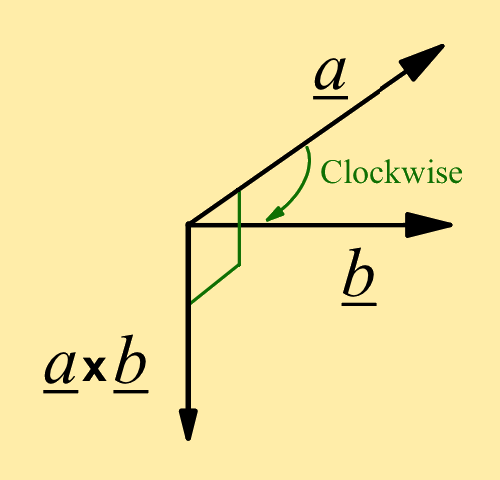
The direction of the vector product of a and b is perpendicular to both a and b:
such that if we look along a×b
then a rotates towards b
in a clockwise manner
|
 |
It can be shown that the above definitions of magnitude and direction of a vector product allow us to calculate the x, y and z components of a × b from the individual components of the vectors a and b
The components of the vector a × b are given by the 'determinant' of a matrix with 3 rows, where the components of a = axi + ayj + azk and b = bxi + byj + bzk appear in the 2nd and 3rd rows.
This 3-row determinant is evaluated by expansion into 2-row determinants, which are themselves then expanded.
Matrix theory is itself very useful, and the scheme is shown below:
| a×b |
= |
|
| |
= |
i |
|
− j |
|
+ k |
|
| |
= |
i(aybz − azby)
−j(axbz − azbx)
+ k(axby − aybx) |
2. Exercises
Click on questions to reveal their solutions
Exercise 1:
Calculate a×b when a = 2, b = 4 and the between a and b is θ = 45°.
Solution:
| a×b |
= |
a b sin θ |
| |
= |
(2) (4) sin 45° |
| |
= |
(2) (4) 1/ √2 |
| |
= |
8/ √2 |
| |
= |
8 / √2 √2 / √2 |
| |
= |
8 √2 /2 |
| |
= |
4√2 |
Exercise 2:
Calculate a×b when a = 3, b = 5 and the between a and b is θ = 60°.
Solution:
| a×b |
= |
a b sin θ |
| |
= |
(3) (5) sin 60° |
| |
= |
(3) (5) √3 /2 |
| |
= |
15/2 √3 |
Exercise 3:
Calculate a×b when a = 1, b = 3 and the between a and b is θ = 30°.
Solution:
| a×b |
= |
a b sin θ |
| |
= |
(1) (3) sin 30° |
| |
= |
(1) (3) 1/2 |
| |
= |
3/2 |
Exercise 4:
Calculate a×b when a = 2, b = 5 and the between a and b is θ = 35°.
Solution:
| a×b |
= |
a b sin θ |
| |
= |
(2) (5) sin 35° |
| |
≈ |
(2) (5) (0.5736) |
| |
≈ |
5.736 |
Exercise 5:
Calculate the magnitude of the torque τ = s×F when s = 2m, F = 4N and θ = 30°, where θ is the angle between the position
vector s and the force F.
Solution:
| τ |
= |
s×F |
| |
= |
s F sin θ |
| |
= |
(2m) (4N) sin 30° |
| |
= |
(2m) (4N) 1/2 |
| |
= |
(8) (N m) 1/2 |
| |
= |
4J |
Exercise 6:
Calculate the magnitude of the velocity v = ω×s when ω = 3m s−1, s = 2m and θ = 30°, where θ is the angle between the angular
velocity ω and the position vector s.
Solution:
| τ |
= |
ω×s |
| |
= |
ω s sin θ |
| |
= |
(3s−1) (2m) sin 45° |
| |
= |
(3s−1) (2m) 1/√2 |
| |
= |
(6) (m s−1) 1/√2 √2 / √2 |
| |
= |
(6) (m s−1) √2 /2 |
| |
= |
3√2 m s−1 |
Exercise 7:
If a = 4i + 2j − k and b = 2i − 6j − 3k calculate a vector that is perpendicular to both a and b
Solution:
| a×b |
= |
|
| |
= |
i |
|
− j |
|
+ k |
|
| |
= |
i[(2)(−3) − (−1)(−6)]
−j[(4)(−3) − (−1)(2)]
+ k[(4)(−6) − (2)(2)] |
| |
= |
i[−6 − 6]
−j[−12 + 2]
+ k[−24 − 4] |
| |
= |
−12i + 10j − 28k |
Exercise 8:
Calculate the vector a×b when a = 2i + j − k and b = 3i − 6j + 2k
Solution:
| a×b |
= |
|
| |
= |
i |
|
− j |
|
+ k |
|
| |
= |
i[(1)(2) − (−1)(−6)]
−j[(2)(2) − (−1)(3)]
+ k[(2)(−6) − (1)(3)] |
| |
= |
i[2 − 6]
−j[4 + 3]
+ k[−12 − 3] |
| |
= |
−4i − 7j − 15k |
Exercise 9:
Calculate the vector a×b when a = 3i + 4j − 3k and b = i + 3j + 2k
Solution:
| a×b |
= |
|
| |
= |
i |
|
− j |
|
+ k |
|
| |
= |
i[(4)(2) − (−3)(3)]
−j[(3)(2) − (−3)(1)]
+ k[(3)(3) − (4)(1)] |
| |
= |
i[8 + 9]
−j[6 + 3]
+ k[9 − 4] |
| |
= |
17i − 9j + 5k |
Exercise 10:
Calculate the vector a×b when a = i + 2j − k and b = 3i + 3j + k
Solution:
| a×b |
= |
|
| |
= |
i |
|
− j |
|
+ k |
|
| |
= |
i[(2)(1) − (−1)(3)]
−j[(1)(1) − (−1)(3)]
+ k[(1)(3) − (2)(3)] |
| |
= |
i[2 + 3]
−j[1 + 3]
+ k[3 − 6] |
| |
= |
5i − 4j −3k |
Exercise 11:
Calculate the vector a×b when a = 2i + 4j + 2k and b = i + 5j − 2k
Solution:
| a×b |
= |
|
| |
= |
i |
|
− j |
|
+ k |
|
| |
= |
i[(4)(−2) − (2)(5)]
−j[(2)(−2) − (2)(1)]
+ k[(2)(5) − (4)(1)] |
| |
= |
i[−8 −10]
−j[−4 + 2]
+ k[10 − 4] |
| |
= |
−18i+ 6j+ 6k |
Exercise 12:
Calculate the vector a×b when a = 3i −4 j + k and b = 2i + 5j − k
Solution:
| a×b |
= |
|
| |
= |
i |
|
− j |
|
+ k |
|
| |
= |
i[(−4)(−1) − (1)(5)]
−j[(3)(−1) − (1)(2)]
+ k[(3)(5) − (−4)(2)] |
| |
= |
i[4 − 5]
−j[−3 − 2]
+ k[15 + 8] |
| |
= |
−i+ 5j+ 23k |
Exercise 13:
Calculate the vector a×b when a = 2i − 3j + k and b = 2i + 6j + 4k
Solution:
| a×b |
= |
|
| |
= |
i |
|
− j |
|
+ k |
|
| |
= |
i[(−3)(4) − (1)(1)]
−j[(2)(4) − (1)(2)]
+ k[(2)(1) − (−3)(2)] |
| |
= |
i[−12 −1]
−j[8 − 2]
+ k[2 + 6] |
| |
= |
−13i−6j+ 8k |
Exercise 14:
Calculate the vector a×b when a = 2i + 3k and b = 2i + j + 4k
Solution:
| a×b |
= |
|
| |
= |
i |
|
− j |
|
+ k |
|
| |
= |
i[(0)(4) − (3)(2)]
−j[(2)(4) − (3)(1)]
+ k[(2)(2) − (0)(1)] |
| |
= |
i[0 −6]
−j[8 − 3]
+ k[4 − 0] |
| |
= |
−6i−5j+ 4k |
3. Alternative Notation
In this Tutorial we use symbols like a to denote a vector. In some texts, symbols for vectors are in bold e.g. a instead of a.
In this Tutorial, vectors are given in terms of the unit Cartesian vectors i, j and k.
A common alternative notation involves quoting the Cartesian components within brackets. For example, the vector a = 2i + j + 5k can be written as a = (2, 1, 5).
The scalar product a⋅b is also called a 'dot product' (reflecting the symbol used to denote this type of multiplication). Likewise, the vector product a×b is also called a 'cross product'.
An alternative notation for the vector product is a∧b.
PPLATO material © copyright 2004, University of Salford


