1. Theory
The purpose of this tutorial is to practice using the scalar product of two vectors. It is called the 'scalar product' because the result is a 'scalar', i.e. a quantity with magnitude but no associated direction.
| NOTE: Throughout this tutorial we use the notation a to denote a vector quantity. However, there are alternative notations, such as a, which are used in the PPLATO Interactive Mathematics modules (see Notation Section). |
The scalar (or 'dot') product of two vectors a and b is:
- where θ is the angle between a and b, and:
- where i, j and k are the unit vectors in the x, y, and z directions, respectively. |
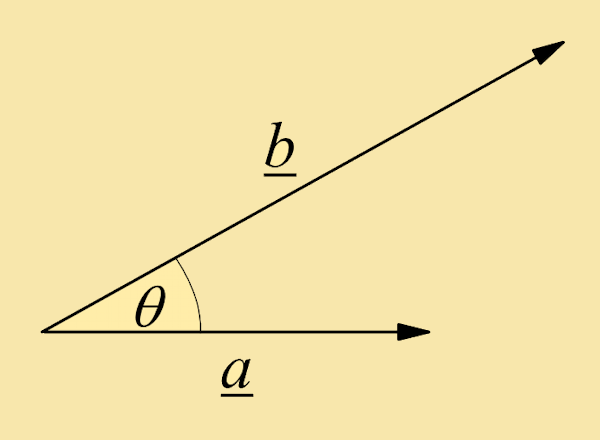 |
The magnitudes of a and b are given by:
2. Exercises
Click on questions to reveal their solutions
Exercise 1:
Solution:
| a⋅b | = | (2)(1) + (−3)(2) + (5)(8) |
| = | 2 − 6 + 40 = 36 |
Exercise 2:
Solution:
| a⋅b | = | (4)(5) + (−7)(−1) + (2)(−4) |
| = | 20 + 7 − 8 = 19 |
Exercise 3:
Solution:
| a⋅b | = | (2)(3) + (3)(−2) + (3)(5) |
| = | 6 − 6 + 15 = 15 |
Exercise 4:
Solution:
| a⋅b | = | (3)(8) + (6)(−3) + (−1)(−1) |
| = | 24 − 18 + 1 = 7 |
Exercise 5:
Solution: For the vectors to be perpendicular requires θ = 90°. Therefore, since a⋅b = a b cos θ, a⋅b = 0. To show that this is true, we use a⋅b = axbx + ayby + azbz :
| a⋅b | = | (1)(1) + (1)(−7) + (3)(2) |
| = | 1 − 7 + 6 = 0 |
Exercise 6:
Solution: For the vectors to be perpendicular requires θ = 90°. Therefore, since a⋅b = a b cos θ, a⋅b = 0. To show that this is true, we use a⋅b = axbx + ayby + azbz :
| a⋅b | = | (1)(26) + (23)(1) + (7)(−7) |
| = | 26 + 23 − 49 = 0 |
Exercise 7:
Solution: For the vectors to be perpendicular requires θ = 90°. Therefore, since a⋅b = a b cos θ, a⋅b = 0. To show that this is true, we use a⋅b = axbx + ayby + azbz :
| a⋅b | = | (1)(2) + (1)(7) + (3)(−3) |
| = | 2 + 7 − 9 = 0 |
Exercise 8:
Solution: For the vectors to be perpendicular requires θ = 90°. Therefore, since a⋅b = a b cos θ, a⋅b = 0. To show that this is true, we use a⋅b = axbx + ayby + azbz :
| a⋅b | = | (39)(1) + (2)(−23) + (1)(7) |
| = | 39 − 49 + 7 = 0 |
Exercise 9:
Solution: F⋅s = F s cos θ = (7N)(3m)(1) = 21J.
Note: When the angle θ is zero then F⋅s = F s and we can simply multiply the magnitudes of F and s.
Exercise 10:
Solution: F⋅s = F s cos θ = (4N)(2m) cos 27° ≈ 7.128J.
Note: F⋅s = F s cos θ can be rewritten as (F cos θ) s. This can be interpreted as being the product of s and the projected component F cos θ along the direction of s. |
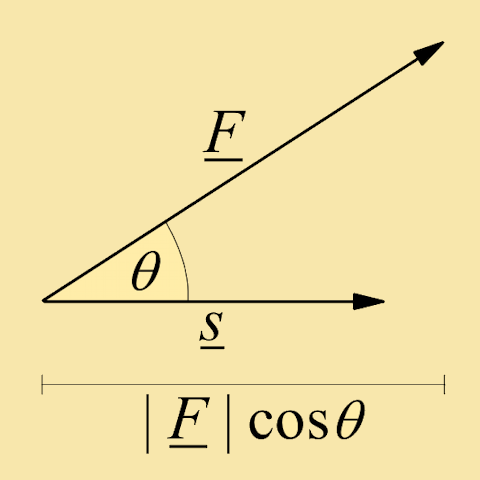 |
Exercise 11:
Solution: F⋅s = F s cos θ = (5N)(4m) cos 48° ≈ 13.38J.
Exercise 12:
Solution: F⋅s = F s cos θ = (2N)(3m) cos 56° ≈ 3.355J.
Exercise 13:
Solution: From a⋅b = a b cos θ, we have:
If we use the Cartesian representation of the two vectors then we have:
| a⋅b | = | axbx + ayby + azbz |
| a | = | √ ax2 + ay2 + az2 |
| b | = | √ bx2 + by2 + bz2 |
For the given vectors these are:
| a⋅b | = | (2)(1) + (−1)(1) + (2)(1) = 2 − 1 + 2 = 3 |
| a | = | √22 + (−1)2 + 22 = √4 + 1 + 4 = √9 = 3 |
| b | = | √ 12 + 12 + 12 = √3 |
so:
Exercise 14:
Solution: From a⋅b = a b cos θ, we have:
If we use the Cartesian representation of the two vectors then we have:
| a⋅b | = | axbx + ayby + azbz |
| a | = | √ ax2 + ay2 + az2 |
| b | = | √ bx2 + by2 + bz2 |
For the given vectors these are:
| a⋅b | = | (1)(2) + (1)(−3) + (1)(1) = 2 − 3 + 1 = 0 |
| a | = | √12 + 12 + 12 = √3 |
| b | = | √22 + (−3)2 + 12 = √4 + 9 + 1 = √14 |
so:
Exercise 15:
Solution: From a⋅b = a b cos θ, we have:
If we use the Cartesian representation of the two vectors then we have:
| a⋅b | = | axbx + ayby + azbz |
| a | = | √ ax2 + ay2 + az2 |
| b | = | √ bx2 + by2 + bz2 |
For the given vectors these are:
| a⋅b | = | (1)(2) + (−2)(3) + (2)(1) = 2 − 6 + 2 = −2 |
| a | = | √12 + (−2)2 + 22 = √1 + 4 + 4 = √9 = 3 |
| b | = | √22 + 32 + 12 √4 + 9 + 1 = √14 |
so:
NOTE:
When a⋅b is positive cos θ is positive and θ is an acute angle |
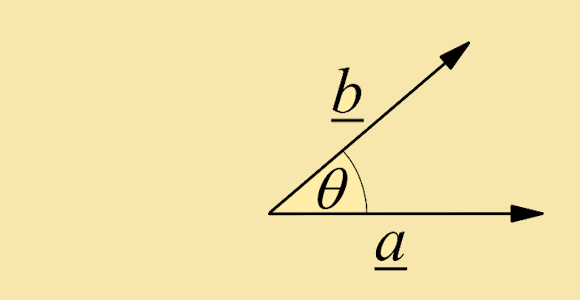 |
When a⋅b is negative cos θ is negative and θ is an obtuse angle |
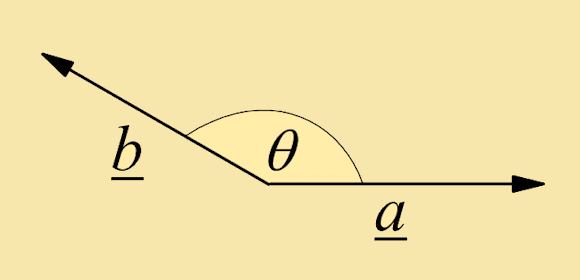 |
Exercise 16:
Solution: From a⋅b = a b cos θ, we have:
If we use the Cartesian representation of the two vectors then we have:
| a⋅b | = | axbx + ayby + azbz |
| a | = | √ ax2 + ay2 + az2 |
| b | = | √ bx2 + by2 + bz2 |
For the given vectors these are:
| a⋅b | = | (5)(4) + (4)(−5) + (3)(3) = 20 − 20 + 9 = 9 |
| a | = | √52 + 42 + 32 = √25 + 16 + 9 = √50 = 3 |
| b | = | √42 + (−5)2 + 32 = √16 + 25 + 9 = √50 |
so:
3. Alternative Notation
In this Tutorial we use symbols like a to denote a vector. In some texts, symbols for vectors are in bold e.g. a instead of a.
In this Tutorial, vectors are given in terms of the unit Cartesian vectors i, j and k. For example, a = i + 2j + 3k implies that a can be decomposed into the sum of the following three vectors as shown below:
|
a = i + 2j + 3k one step along the x-axis two steps along the y-axis three steps along the z-axis |
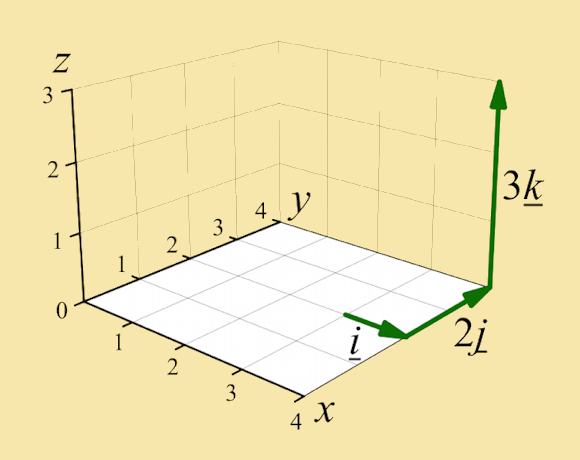
|
a is the (vector) sum of i and 2j and 3k |
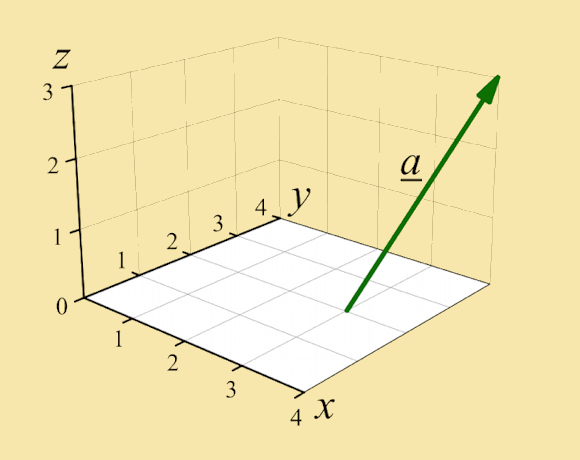
|
A common alternative notation for expressing a in terms of these Cartesian components is given by a = (1, 2, 3).
