PHYS 9.1: Introducing atomic nuclei |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
The atom of any element is made up of a tiny, positively charged nucleus surrounded by negatively charged electrons. The nucleus, although small, contributes almost all of the mass of an atom. The chemical properties of materials are almost independent of the structure of the nucleus, since they arise from the interactions of the electrons in the atoms or molecules of the material. In contrast many other processes, such as the release of energy by the Sun and by terrestrial nuclear energy sources, depend crucially on the properties of the nucleus. Therefore a knowledge of the nucleus is essential for understanding these processes.
In this module we will discuss the basic properties of nuclei, starting with their charge and mass. In Section 2 we will discuss the basic nuclear constituents – nucleons (a collective name for protons and neutrons) and the meaning of terms such as mass number and atomic number used to describe nuclei. We will also explain the nature of isotopes, and introduce the atomic mass unit. Next (in Section 3), we will consider the forces between particles in the nucleus and introduce the strong interaction between nucleons. A discussion of nuclear binding energy and nuclear mass will enable us to relate the mass defect of a nucleus to the energy released in a nuclear reaction via Einstein’s energy–mass equation. Finally, in Section 4, we will apply these ideas to unstable nuclei and radioactive decay, introduce the Q-value of a reaction and use it to predict which reactions may occur and which are forbidden.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the folllowing Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
How many neutrons and protons are there in 2210Ne and 9440Zr nuclei?
Answer F1
The nucleus ${}^A_Z{\rm X}$ is the nucleus of an atom of chemical element X. It has atomic number Z, which means that ithas Z protons. It has mass number A, which means that it has a total of A nucleons, i.e. (A − Z) neutrons.
So the nucleus 2210Ne} has 10 protons and 12 neutrons and the nucleus 9440Zr} has 40 protons and 54 neutrons.
| Z | Element | Symbol | A | Atomic mass/u | Relative abundance/% |
|---|---|---|---|---|---|
| 1 | hydrogen | H | 1 | 1.007 825 | 99.985 |
| 2 | 2.014 102 | 0.015 | |||
| 2 | helium | He | 4 | 4.002 603 | 99.999 |
| 79 | gold | Au | 197 | 196.966 560 | 100 |
| 82 | lead | Pb | 204 | 203.973 037 | 1.4 |
| 206 | 205.974 455 | 24.1 | |||
| 207 | 206.975 885 | 22.1 | |||
| 208 | 207.976 641 | 52.4 | |||
| 83 | bismuth | Bi | 209 | 208.980 388 | 100 |
| * The neutron, in the free state, is not stable; it has a mean lifetime of approximately 15 min. It has a mass of 1.008 665 u. In contrast, a free proton is stable and has a mass of 1.007 276 u. | |||||
Question F2
Calculate, using data from the table the binding energy of the nucleus of 20882Pb in units of MeV.
(1 u = 931.502 MeV/c2)
Answer F2
Properties of some common nuclides
The nucleus 20882Pb has 82 protons and 126 neutrons; from the table its mass is 207.976 641 u. The total mass of the free neutrons and protons is
82 × 1.007 825 u + 126 × 1.008 665 u = 209.733 44 u
(again using Table 1). The mass defect is, therefore, 209.733 44 u − 207.976 641 u = 1.7568 u.
The binding energy in MeV (from E = mc2) is therefore given by:
binding energy = 1.7568 × 931.502 (MeV/c2) × c2 = 1636.5 MeV
1.3 Ready to study?
Study comment In order to study this module you will need to understand the following terms: atom, charge (and its SI unit, the coulomb), chemical symbol, electric field, electron, electrostatic force, electric potential difference, element, energy (and its SI unit, the joule), conservation_of_energyenergy conservation, gravitational force, ion, kinetic energy, magnetic field and mass. If you are uncertain about any of these terms then you can review them by reference to the Glossary, which will also indicate where in FLAP they are developed. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
Do like charges attract or repel?
Answer R1
Like charges (i.e. both positive or both negative) repel each other.
Question R2
An electron is accelerated from rest through a potential difference of 5 V. Determine the increase in kinetic energy of the electron in joules. i
Answer R2
The energy Eel transferred when a charge q is accelerated through a potential difference V is Eel = qV. An electron has a charge of magnitude 1.602 × 10−19 C so the energy transferred to the electron in accelerating it through 5 V is Eel = 5 V × 1.602 × 10−19 C = 8.010 × 10−19 J. This is equal to the kinetic energy acquired by the electron.
Question R3
State Newton’s law of universal gravitation. Is the force involved attractive or repulsive?
Answer R3
Newton’s law of universal gravitation states that every body attracts every other body with a force proportional to the mass of each and inversely proportional to the square of the distance of separation. For bodies with masses m1and m2 separated by a distance r the magnitude of the force Fgrav is:
$F_{\rm grav} = G\dfrac{m_1m_2}{r^2}$
where G is the universal gravitational constant.
(If you feel unsure about any of the terms used in Questions R1 to R3, consult the Glossary.)
2 The structure of the nucleus
2.1 The contents of nuclei
The scattering of charged particles by a thin metal foil, a phenomenon investigated by Hans Geiger (1882–1945) and Ernest Marsden (1889–1970) in 1909 and interpreted by Ernest Rutherford (1871–1937) in 1911, revealed that the atomic nucleus is very small. The order of magnitude of a nuclear diameter, 10−14 m, is tiny compared with the typical atomic diameter of 10−10 m. i Nonetheless, experiments have shown that the nucleus has its own internal structure. But what are the constituents of the nucleus? The nucleus of one particular kind of atom, the atom of hydrogen, is very simple. The single electron in a hydrogen atom may be detached to leave a nucleus that consists of a single, stable particle called the proton. i A proton has a charge +e, i and its mass, mp, is 1.673 × 10−27 kg, i.e. about 1840 times that of the electron. i Protons are responsible for the net positive charge of each kind of nucleus, but is the proton the sole building block of all nuclei? We will consider this as a physicist should – by logical analysis, tested by reference to experiment. Consider, as an example, the nucleus of the element silicon. A silicon atom has 14 electrons, and since the atom as a whole is electrically neutral, the silicon nucleus must therefore have a charge of +14e. This means that the nucleus must contain 14 protons, and that its mass would be about 14mp if it contained only protons. So we have a prediction; how may we test it?
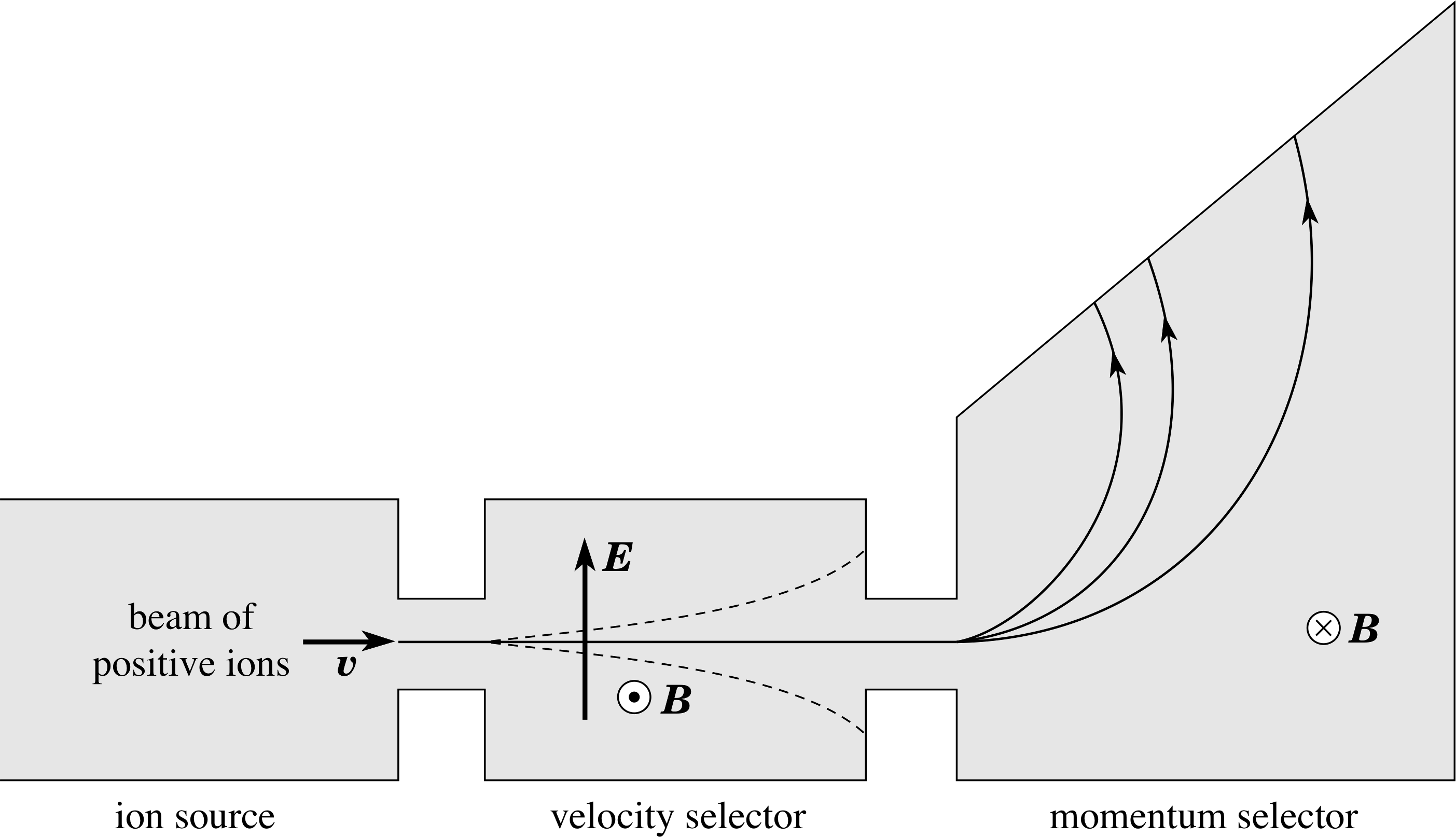
Figure 1 Diagrammatic representation of a mass spectrometer. The direction of the magnetic fields in the velocity and momentum selectors are indicated by arrows. The symbol represents an arrow coming out of the page, ⊗ represents an arrow going into the page. The velocity selector uses the relation, qE = qυ × B, i.e. electrons with a speed given by υ = E/B are passed. The momentum selector uses the relation, mυ2/r = qυB, i.e. mυ = qBr. Therefore for a given charge, each trajectory corresponds to a different momentum.
The principle used in the measurement of the mass of a nucleus is that charged particles are deflected by both electric and magnetic fields. i The instrument for measuring atomic and nuclear masses – a mass spectrometer – has three parts (see Figure 1).
The first part is the ion source in which the atoms of the element are stripped of one or more of their electrons. The positively charged ions produced are accelerated and emerge from the ion source into the velocity selector. The electric and magnetic fields in this region are uniform along the path of the beam and are mutually perpendicular to each other and to the direction of motion of the beam. The magnitudes of these fields are adjusted to select the speed of the ions that will pass into the final chamber (the momentum selector), where there is only a uniform magnetic field. As the ion beam passes through this magnetic field it is deflected in a direction at right angles to that of the field. (see Figure 1). The radius of curvature of the path along which the deflected ion travels in this region depends on its charge to mass ratio and hence (provided all the ions have the same charge) this radius enables its mass to be determined. Since the mass of an ion is due almost entirely to the nuclear mass, this may then be deduced from the ion mass.
Let us now return to our prediction. Is the mass of the nucleus of silicon equal to 14mp? You can imagine the disappointment of an early experimenter when it was discovered that this mass turned out to be about 28mp. There must be some other constituent of the nucleus.
The answer to the puzzle was not discovered until, in 1932, James Chadwick (1891–1974) detected another particle of about the same mass as the proton, but with no charge. This particle is the neutron. The mass of our nucleus of silicon is now explained if it contains 14 neutrons in addition to its 14 protons – then both charge and mass are accounted for.
It turns out that all elements (with the exception of hydrogen, where the nucleus is just a single proton i) have a nucleus consisting of protons and neutrons. Since they make up all nuclei, protons and neutrons are known collectively as nucleons. This is used in the following notation to characterize any nucleus.
The atomic number, Z, specifies the number of protons in the nucleus. The total number of nucleons is called the mass number, A.
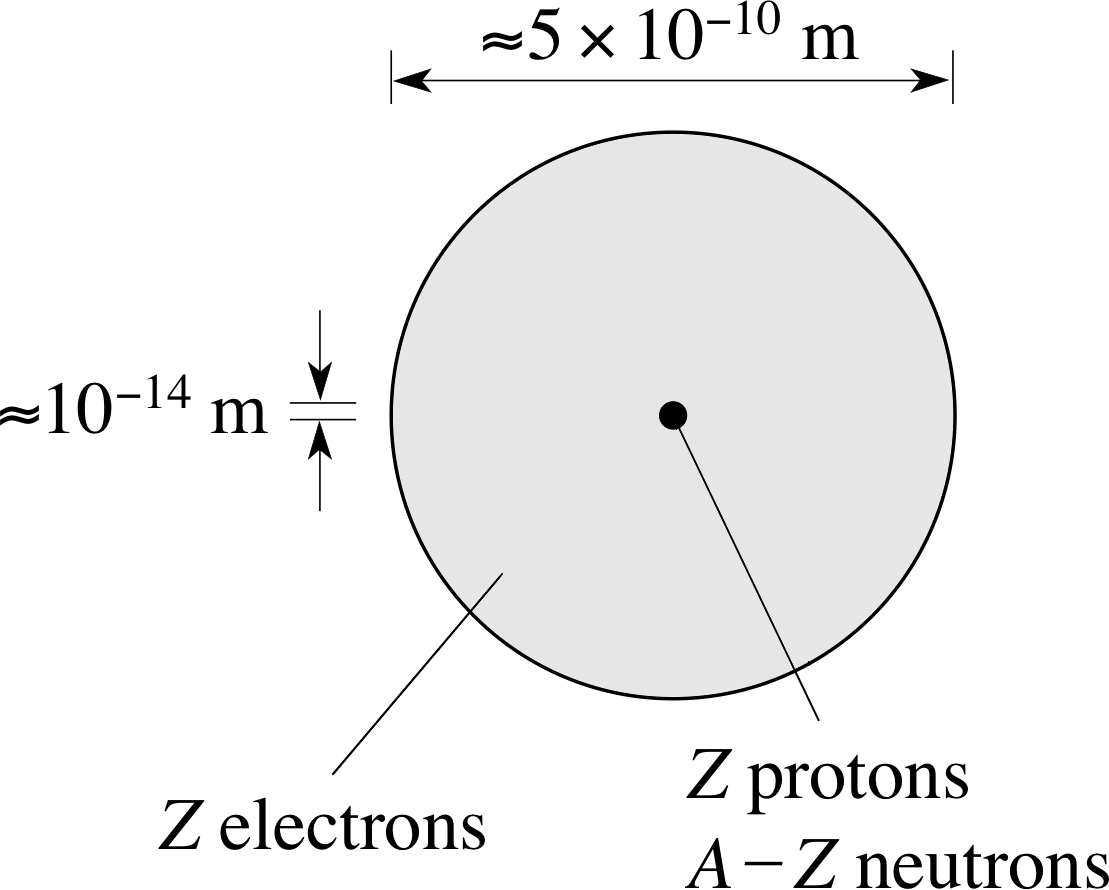
Figure 2 An atom contains Z electrons, Z protons and (A − Z) neutrons, where Z is the atomic number of the nucleus and A its mass number.
In our silicon example, Z = 14, A = 28. In a neutral atom, the charge on the nucleus is balanced by the charge of the surrounding electrons, and so there must be Z electrons. Since it is the electrons that determine the chemical properties of an atom, Z defines the chemical element and determines its place in the Periodic Table of the elements. i
Z specifies the charge on the nucleus in units of e, whereas A gives the total number of nucleons and so relates to its mass. This is illustrated in Figure 2.
✦ Do we need another independent number to specify the number of neutrons?
✧ No. The number of neutrons (sometimes given the symbol N) is equal to (A − Z).
We denote the nucleus of any element by the chemical symbol of its atom with Z as a subscript and A as a superscript before the symbol, i.e. as ${}^Z_A{\rm X}$, where X is the chemical symbol of the element.
Question T1
Use this notation to write the symbol for a silicon nucleus, given that Z = 14, A = 28 and its chemical symbol is Si. Is this notation as brief as possible?
Answer T1
2814Si. Strictly speaking the notation ${}^A_Z{\rm X}$ is not as brief as it could be because the number Z can refer only to one chemical symbol X. For instance 2814Si can refer only to silicon since Z = 14. Therefore either Z or X could be left out of the notation. But redundant chemical information is not necessarily a bad thing; here it reminds the reader of the chemical element with this value of Z and checks that the information is consistent. This notation has become standard.
Following the development and refinement of the mass spectrometer in the 1930s, the masses of all available stable nuclei were measured. Some results were unexpected. It was found that the nuclei from atoms of a particular chemical element, characterized by a particular value of Z, did not all have the same mass number A.
As they all have the same number of protons – namely Z – they must differ in their numbers of neutrons.
Atoms of a particular element that differ only in the number of neutrons they contain are called isotopes of that element. i For example, silicon has three common isotopes, 2814Si, 2914Si and 3014Si, which occur naturally with relative proportions of 92%, 5% and 3%, respectively. The term nuclide is often used to denote the atom of an element distinguished by the number of neutrons in its nucleus. i
Question T2
Consider the isotope 6830Zn of the element zinc.
(a) How many protons does the nucleus contain?
(b) How many neutrons does the nucleus contain?
(c) Given that the charge on the electron is approximately −1.6 × 10−19 C, what is the charge on the nucleus?
(d) How many electrons are there in a neutral atom of zinc?
(e) A nucleus X has atomic number 31. Is X an isotope of zinc?
Answer T2
The nucleus of the isotope 6830Zn has (a) 30 protons, and (b) 68 − 30 = 38 neutrons.
(c) The charge on the nucleus is 30 × (+1.6 × 10−19 C) = +4.8 × 10−18 C.
(d) The neutral atom has the same number of electrons as protons. Therefore it contains 30 electrons.
(e) Nucleus X has 31 protons, whereas zinc always has 30, therefore X cannot be the chemical element zinc – it is actually the element gallium.
Masses of nuclei are extremely small. The silicon isotope 2814Si has a mass of about 4.65 × 10−26 kg. Such small numbers would be very tiresome to work with so, just as charges are quoted in units of e, atomic masses are quoted not in kg but in their own more appropriately sized unit, the atomic mass unit, u.
The atomic mass unit (u) is defined so that the mass of the most common isotope of the carbon atom, with a 126C nucleus, is exactly 12 u. So 1 u = 1.6606 × 10−27 kg.
Note that the unit is defined in terms of the mass of the atom and not the mass of the nucleus. The mass of an atom and its nucleus, for simple purposes, will be used in this module as if they were the same – they differ by approximately the mass of Z electrons.
Table 1 gives the atomic masses of a few elements, listed in order of increasing atomic number. i
Question T3
If the mass of the electron is 9.110 × 10−31 kg, estimate the mass of the 126C nucleus. By what percentage does this differ from 12 u?
Answer T3
The atom of 126C has six electrons of total mass 6 × (9.110 × 10−31 kg) = 5.4654 × 10−30 kg. This mass in atomic mass units u is:
$\rm \dfrac{5.4654\times10^{-30}\,kg}{1.6606\times10^{-27}\,kg\,u^{-1}} = 3.291\times10^{-3}\,u$
The mass of the 126C nucleus is the mass of the atom minus the mass of the electrons, i.e.
(12 − 3.291 × 10−3) u = 11.996 709 u
The percentage is therefore (3.291 × 10−3/12) × 100 = 0.027%.
Note This is for a light nucleus, with an equal number of protons and neutrons. For heavier nuclei, there are more neutrons than protons in the nucleus, so the electrons contribute a smaller percentage of the atomic mass. For precise nuclear calculations, such as you will encounter later in this module, the actual masses of nuclei should be used, but for many purposes the mass of the nucleus can be taken to be the same as the mass of the atom.
An important feature of nuclear structure can be visualized by plotting the number of neutrons (N = A − Z) in a stable i nucleus against the number of protons (Z). This is shown in Figure 3, where each point represents a completely stable nucleus (i.e. one that never disintegrates). If there is no point shown at coordinate (Z, N) then no stable nucleus exists with that number of protons and neutrons. Figure 3 is therefore a useful chart which gives the number of stable isotopes for any given nucleus. For instance, we can see that chlorine with atomic number 17, has two entries on the vertical line through Z = 17, one at A − Z = 18 and the other at A − Z = 20. There are therefore two stable isotopes of chlorine, 3517Cl and 3717Cl. But the question arises, why do neutrons and protons bind together to form nuclei? We will look at this in the next subsection.
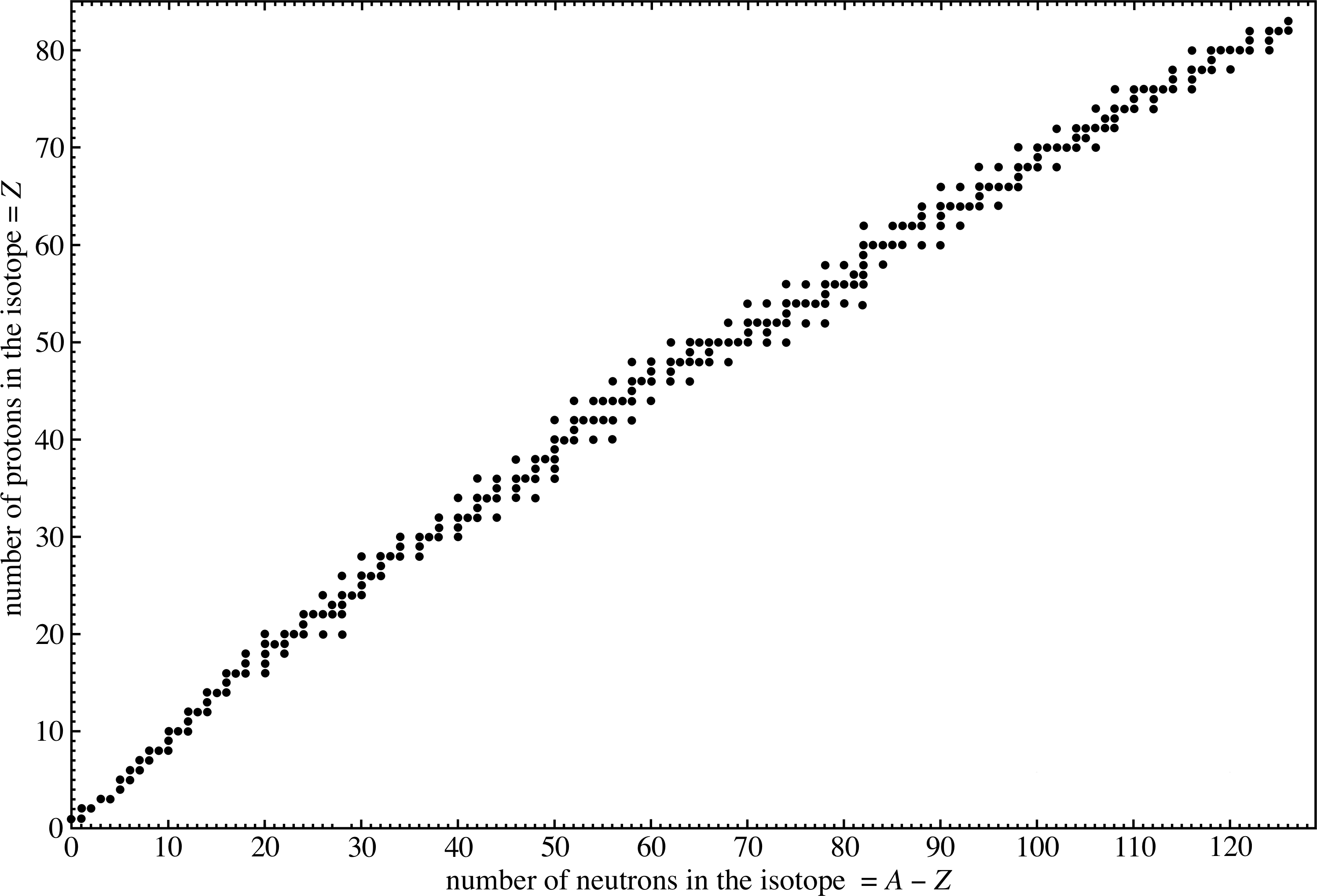
Figure 3 The number of neutrons in completely stable nuclei plotted against the number of protons that they contain. (The Z–axis of this graph could be extended to 90, but no new completely stable nuclei have been found beyond Z = 83).
2.2 The strong interaction between nucleons
The term interaction_fundamentalinteraction is used to describe a fundamental force underlying the behaviour of particles. i When the existence of nuclei was discovered there were only two known ways in which neutrons and protons within a nucleus might interact. One interaction produced the gravitational force – all bodies with mass attract each other. The other produced the electrostatic force between charged particles – attractive or repulsive. Both protons and neutrons have mass, so the gravitational interaction tends to hold them together. Only protons have charge and in the nucleus they repel each other, opposing stability. If these were the only forces within the nucleus, which would ‘win’? We can answer this by calculating the strength of the attractive force between two protons due to gravity, and comparing the result with their mutual repulsion due to their like charges.
Two protons, each of mass mp and charge e, separated by a distance r, attract each other with a gravitational force of magnitude Fgrav and repel each other with an electrostatic force of magnitude Fel where
$F_{\rm grav} = \dfrac{Gm_{\rm p}^2}{r^2}\quad\text{and}\quad F_{\rm el} = \dfrac{e^2}{4\pi\varepsilon_0r^2}$
(G is the universal gravitational constant and ε0 the permittivity of free space.) i
✦ Given that ε0 = 8.854 × 10−12 C2 N−1 m−2 and G = 6.673 × 10−11 N m2 kg−2, work out the units of the ratio Fgrav/Fel.
✧ The units of Fgrav are $\rm \dfrac{N\,m^2\,kg^{-2}\times kg^2}{m^2} = N$ and the units of Fel are $\rm \dfrac{C^2}{C^2\,N^{-1}\,m^{-2}\times m^2} = N$.
As expected the ratio Fgrav/Fel is dimensionless.
Calculation of the ratio of the gravitational force to the electrostatic force gives a value which is of the order of 10−36. Notice that the separation r is immaterial since the factor 1/r2 cancels in the ratio. The gravitational force is exceptionally weak and quite unable to counteract the repulsion between the protons. Therefore there must be another attractive force, to account for stable nuclei.
The strong attractive force which is responsible for holding nuclei together is called, somewhat unimaginatively, the strong nuclear force or the strong interaction between nucleons. It arises from an interaction between the particles that is fundamentally different from the interactions that give rise to the electrostatic and gravitational forces – it depends neither on charge nor mass. i Let us look at Figure 3 again to see what hints it can give us about the nature of this third interaction.
✦ Place a ruler along the line N = Z on Figure 3. This line joins points corresponding to equal numbers of protons and neutrons. What do you observe?
✧ The plot of stable nuclei (the stability line) roughly follows the line N = Z as Z increases from 1 until about Z = 17, but after that the stability line increasingly diverges, remaining always above the line N = Z. As Z increases there are increasingly more neutrons than protons in stable nuclei.
Question T4
From Figure 3, calculate the ratio of the number of neutrons to the number of protons for the nucleus with atomic number 69. What is the corresponding value for the nucleus with Z = 79?
Answer T4
From Figure 3, the point corresponding to Z = 69 is N = 100 (there is only one isotope). The neutron/proton ratio therefore is 100/69 = 1.45. For Z = 79, N = 118 the ratio is 1.49.
(The ratio increases with increasing Z, as is evident from the general trend of the points plotted.)

Figure 3 The number of neutrons in completely stable nuclei plotted against the number of protons that they contain. (The Z–axis of this graph could be extended to 90, but no new completely stable nuclei have been found beyond Z = 83).
Figure 3 shows that the larger the number of neutrons and protons in the nucleus, the greater must be the neutron to proton ratio. It also shows that no stable nuclei exist with Z > 83. i
What clues does Figure 3 give us about the nature of the strong interaction between nucleons?
- Since it is the number of neutrons that affects nuclear stability, we can deduce that neutrons also experience the strong nuclear interaction.
- For small nuclei there are about equal numbers of neutrons and protons (line N = Z). This suggests that the strong nuclear interaction does not discriminate between neutrons and protons – it is charge-independent.
- As the number of protons increases, their mutual electrostatic repulsion must increase so it requires proportionally more and more neutrons to stabilize the nucleus. The addition of more neutrons increases the nuclear attraction without adding electrostatic repulsion. Presumably also, this may increase the mean distance between the protons and so reduce the electrostatic repulsion. This explains why the stability line veers away from the line N = Z as Z increases.
- As Z increases, eventually the nuclear force is unable to stabilize the nucleus against the electrostatic repulsion. No fully stable nucleus occurs with Z > 83. i
So, even the strong interaction between nucleons is insufficient to overcome the electrostatic repulsion in all circumstances. This hints at the limited range of effectiveness of the strong interaction.
The electrostatic force diminishes as the inverse square of the separation of the interacting charges (i.e. Fel ∝ 1/r2). This is a relatively slow rate of reduction with distance; so the electrostatic force is effective over a relatively long range.
Suppose that the strong interaction decreases with distance with a higher power of r (so that it is effectively zero at about 10−14 m), what would be the consequence of this? In this case, unlike that of charge repulsion, nucleons would interact strongly only with their nearest neighbours in the nucleus. This means that each nucleon makes a more or less fixed contribution to the attractive force within a moderate to large nucleus, irrespective of the total number of nucleons present. Consequently, as the nucleus increases in size, the total attractive force due to the strong interaction increases approximately in proportion to the total number of nucleons (i.e. ∝ A). However, the long–range electrostatic repulsion would allow each proton to repel all other protons in the nucleus, not just nearest neighbours. The total repulsive force therefore depends on the number of pairs of protons which experience the force. As the nuclear size increases this repulsion increases approximately in proportion to the square of the total number of protons (i.e. ∝ Z2). i At some value of Z the strong attraction between nucleons will be unable to sustain the nucleus against the electrostatic repulsion. This seems to occur at Z = 83.
Let us review our tentative conclusions:
The strong interaction between nucleons has four characteristics:
- It is attractive.
- It is independent of the charge and mass of the interacting particles – the neutron–proton, proton– proton and the neutron–neutron strong interactions are the same.
- The interaction has a very short range (about 10−14 m).
- The interaction consequently must be very strong.
We will now look at some further evidence about the magnitude of the strong interaction. To do this we will need to introduce the concept of binding energy. This is the subject of the next section.
3 Nuclear energies and masses
3.1 Nuclear binding energy
In general, any system is stable when it has the lowest possible energy. A collection of nucleons bound together in a stable nucleus must therefore have a lower energy than these same nucleons as a collection of free particles. If this were not so, the nucleus would spontaneously disperse into its constituents; it would decay rather than be stable. The difference between the energy of the constituents if just free (that is with no kinetic energy) and the energy of the bound nucleus is called the binding_energy_of_a_nucleusnuclear binding energy. Expressed another way, the nuclear binding energy is the energy that must be given to the nucleus in order that all of its constituents may just break free. Binding energy is a similar concept to ionization energy – the energy needed just to separate an electron from an atom, leaving a positive ion i – only with nuclear binding energy we are considering the complete dismantling of the nucleus into its constituent nucleons, rather than removing just one of them.
Let us look first at the magnitude of binding energies and, as with the nuclear masses earlier, define an appropriate unit for this measurement. To take an example, breaking up a helium nucleus, 42He, into its two protons and two neutrons requires approximately 5 × 10−12 J. On an everyday–scale this is a very small amount of energy so it can be measured in terms of a very small energy unit.
The energy units customarily used in atomic and nuclear physics are based on the electronvolt (eV), which is the kinetic energy gained by an electron when it is accelerated through a potential difference of one volt. This is equal to 1.602 × 10−19 J. So 1 eV = 1.602 × 10−19 J.
The eV is the unit which is appropriate for atomic physics. For instance, it takes about 13.6 eV to ionize a hydrogen atom. But as you can see in the example of helium, the eV is much smaller than a typical nuclear binding energy, so in nuclear physics the megaelectronvolt, MeV, is used: 1 MeV = 106 eV = 1.602 × 10−13 J. The binding energy of 42He is 28.3 MeV. i
Question T5
A proton is accelerated through a potential difference of 1 kV. How much kinetic energy is transferred to the proton? Give the answer both in joules and MeV.
Answer T5
The kinetic energy acquired by the proton is
1.602 × 10−19 C × 103 V = 1.602 × 10−16 J = 103 eV = 10−3 MeV.
Experimentally, binding energies of stable nuclei are found to vary from about 2 MeV to about 2000 MeV. As you will see later, data on binding energies can be used to consolidate our tentative inferences about the strong interaction between nucleons. First, however, we will see how binding energies may be deduced from measurements of nuclear masses with the help of Einstein’s famous relationship between mass and energy.
3.2 Nuclear masses and Einstein’s equation
If you were to approach a person in the street and ask them to tell you a scientific formula, they would probably mention the equation E = mc2. This equation is a result from Einstein’s special theory of relativity, the details of which do not concern us here; you will doubtless meet it elsewhere in your studies. i The result may be stated in words as follows: ‘An amount of energy (of any type) has an equivalent mass’ or more specifically, the amount of energy E equivalent to a mass m is given by
Einstein’s mass–energy equation:
E = mc2(1)
where c is the speed of light in a vacuum, approximately 2.998 × 108 m s−1. The energy that an object has purely by virtue of its mass is often called its mass energy. i Equation 1 is so important in nuclear physics that it will be referred to by name. We will use the equation here to relate the measured masses of nuclei to their binding energies, and thus to deduce the binding energies from purely empirical data about masses.
But let us first gain some feeling for the size of the energies involved in relation to everyday energy units (joules) and to nuclear units (MeV). The mass which is equivalent to one joule is given by Equation 1 as:
$\text{mass equivalent of }1\,{\rm }J\text{ of energy} = \rm \dfrac{\, J}{(2.998\times10^8\,m\,s^{-1})^2} \approx 10^{-17}\,kg$
It is not surprising that Einstein’s equation started life (in 1905) as a theoretical speculation. With the instrumentation available at the time, masses of this order could not have been detected experimentally.
But in the atomic and nuclear domain we are familiar with masses and energies which are many orders of magnitude less than the everyday scale. Let us look for instance at the proton mass, mp, which is 1.673 × 10−27 kg. The corresponding energy, mpc2, is equal to 1.503 × 10−10 J or approximately 938 MeV in nuclear units.
Note that mass has the dimensions of energy divided by speed squared: this can be seen both from Einstein’s equation and the familiar expression for kinetic energy, $E_{\rm kin} = \frac12m\upsilon^2$. Einstein’s equation can be rearranged to give m = E/c2, and this leads to a convenient unit for mass.
When working in nuclear units, with energy in units of MeV, it is common to express masses of nuclear particles in units of MeV/c2. The mass of a particle, in MeV/c2, is numerically the same as its energy equivalent in MeV.
In our example the mass of the proton is 938 MeV/c2. The energy equivalent of the mass is then obvious, it is 938 MeV.
Question T6
The mass of the electron, me, is 9.110 × 10−31 kg. What is the energy equivalent of this mass in J and in MeV? Express the mass of the electron in MeV/c2.
Answer T6
The energy equivalent for the mass of an electron is
mec2 = 9.110 × 10−31 kg × (2.998 × 108 m s−1)2 = 8.188 × 10−14 J
Since 1 eV = 1.602 × 10−19 J, the energy equivalent to the mass of the electron is therefore
$\rm \dfrac{8.188\times10^{-14}\,J}{1.602\times10^{-19}\,J\,eV^{-1}} = 5.111\times10^5\,eV = 0.511\,MeV$
The electron therefore has a mass of 0.5111 MeV/c2 (i.e. the mass which, when multiplied by c2 gives
0.5111 MeV).
Question T7
We have seen in Subsection 2.1 that the atomic mass unit (1 u) is equal to 1.6606 × 10−27 kg. Using the same approach as in Question T6, express the magnitude of 1 u in units of MeV/c2.
Answer T7
1 u = 1.6606 × 10−27 kg. Using the same method as in the answer to Question T6, we find:
$1\,{\rm u} = \dfrac{1.6606\times10^{-27}\,{\rm kg}\times\left(2.998\times10^8\,{\rm m\,s^{-1}}\right)^2}{1.602\times10^{-19}\,{\rm J\,eV^{-1}}} = 9.317\times10^8\,{\rm eV}/c^2 = 931.7\,{\rm MeV}/c^2$
(A more precise figure obtained using a more precise value of c and e is 1 u = 931.502 MeV/c2).
In the context of the physics of the nucleus, Einstein’s equation provides an explanation for a phenomenon which would have sorely troubled a 19th-century physicist – the so–called missing mass. Let us examine this through an example. We will take the most common oxygen isotope 168O, which has eight protons and eight neutrons. From Table 1 we may calculate the mass of the constituents:
8mp + 8mn = (8 × 1.007 825 u) + (8 × 1.008 665 u) = 16.131 920 u i
However, the measured mass of the 168O nucleus is 15.994 915 u. This is less than the mass of the constituents.
The difference, 0.137 005 u, is known as missing mass or mass defect. Every nucleus (with the exception of 11H) has a mass defect. This would have been incomprehensible to 19th-century physicists who regarded mass as the quantity of matter in a body. They would have said ‘how could matter have possibly disappeared from the constituents merely by their being part of a bound system?’ But if energy can be considered as having an equivalent mass then there is a simple explanation; the mass defect is simply the mass equivalent of the binding energy – the energy that has been ‘saved’ by binding the nuclear constituents together.
This explanation is based on a revised view of mass and energy conservation. In the 19th century we had two separate principles, the conservation of energy and the conservation of mass. Now, following Einstein’s introduction of the concept of mass energy, we have a single principle, the conservation of relativistic energy in which the total energy of a body of mass m includes its mass energy mc2.
Applying this new principle to a nucleus we can write:
mass energy of free particles = mass energy of nucleus + binding energy of nucleus
So, upon dividing both sides by c2 we get:
mass of free particles = mass of nucleus + (binding energy of nucleus)/c2
Sincemass defect = mass of free particles − mass of nucleus, it follows that:
mass defect = (binding energy of nucleus)/c2(2)
The above expressions tell us that any stable nucleus (i.e. one that requires an input of energy in order to separate its nucleons) must have less mass than the sum of the masses of its free constituent nucleons. So the mass defect is an inevitable consequence of special relativity as expressed in Einstein’s equation.
Question T8
Calculate the mass defect for 126C. Express this in units of u and in MeV/c2. What is the binding energy of 126C?
Answer T8
From the data in Subsection 3.2 and the definition of the above mass unit the mass defect is:
(6 × 1.007 825) u + (6 × 1.008 665) u − 12 u = 0.098 94 u
Using the answer to Question T7 (i.e. 1 u = 931.7 MeV/c2), the mass defect is 92.18 MeV/c2, and hence the binding energy is 92.18 MeV.
3.3 The nuclear binding energy graph
The calculation in Question T8 can of course be repeated using the mass measurements of all stable nuclei. As mentioned in Subsection 3.1, the values of the binding energies vary from 2 MeV for the lightest nucleus to almost 2000 MeV for the heaviest. More enlightening information on the stability of nuclei and the nature of the strong interaction itself comes from a plot of the binding energy per nucleon against the mass number A. This graph is usually called the nuclear binding energy graph and it is shown in Figure 4. As the binding energy of a nucleus is the minimum energy required to ‘unbind’ the nucleus into free protons and neutrons, the binding energy per nucleon is simply the binding energy divided by the mass number A.
Figure 4 shows all stable and some unstable nuclei. In Section 4 we will look at unstable nuclei, but let us first concentrate on the stable nuclei – shown as filled dots in Figure 4.
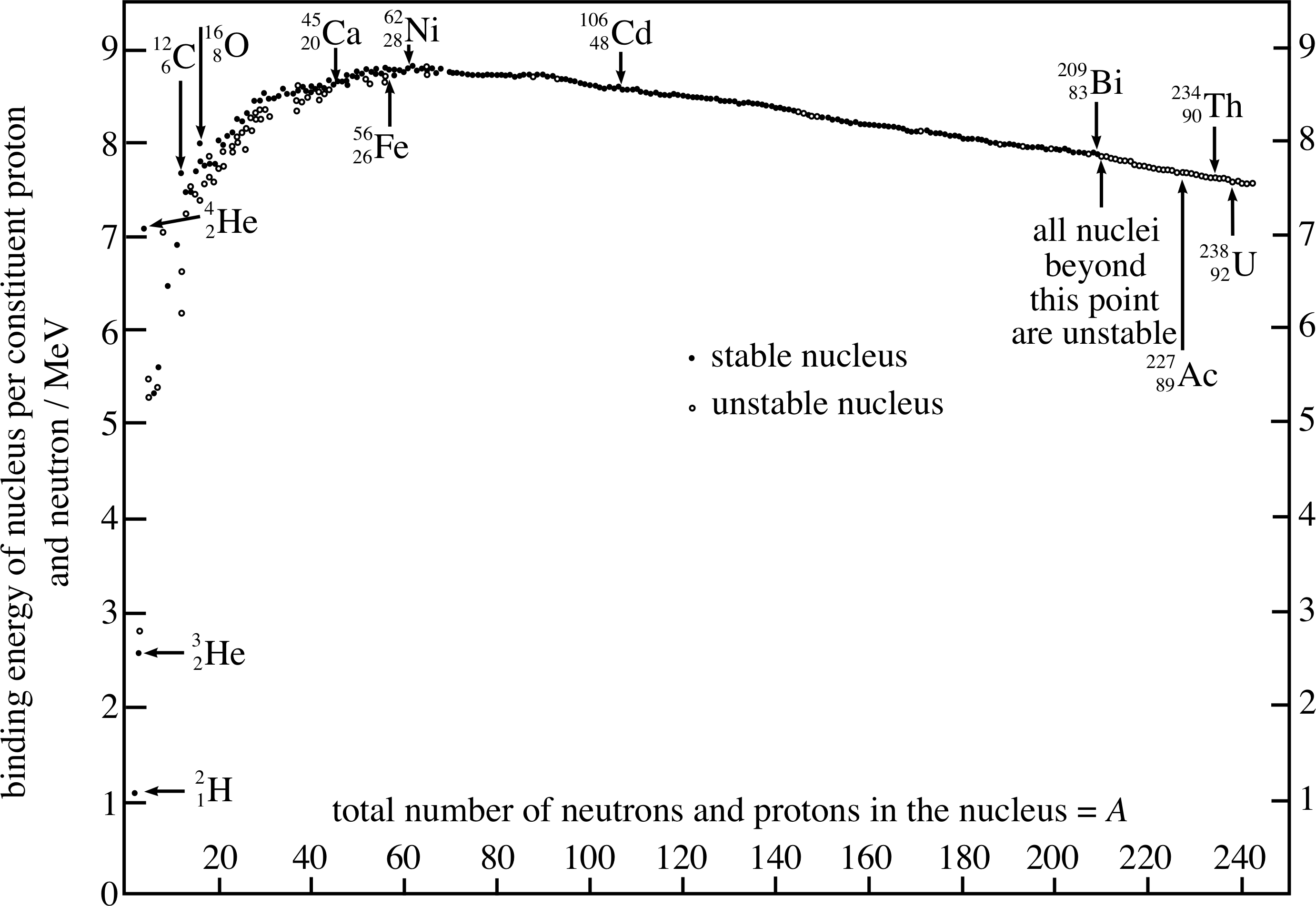
Figure 4 The nuclear binding energy graph.
The graph may be analysed in three parts.
- In the first part of the graph (from A = 1 to about 30) the nucleus is becoming established as a stable unit, the mean binding energy per nucleon is rising as each nucleon surrounds itself with a full complement of other nucleons as near neighbours with which it can interact attractively. In this region protons and neutrons can be added equally easily since the effect of the weak electrostatic repulsion is small. Notice, however, that even within this steeply rising part of the curve there are one or two striking anomalies in the relatively smooth curve. Most significant is the nucleus of helium 42He, which appears to be much more stable than its general position at A = 4 might suggest. (126C and 168O are similar, but less striking anomalies.) It is no surprise then to find that the nucleus of helium often emerges as a separate entity from the decay of other unstable nuclei – it is the alpha_particleα–particle (alpha-particle), of which more will be said later in this module.
- In the second part of the graph (from A = 30 to about 100) the mean binding energy stays about constant at around 8.5 MeV/nucleon. This is the region where the nuclear binding interaction is in competition with the unbinding influence of the electrostatic repulsion between the protons. Since the latter is increasing as Z2 while the attraction is only increasing as A, the repulsion must eventually ‘win out’. In the first part of the middle region the attraction is a slight winner and in the final part it is a slight loser.
- In the third part of the graph (A > 100) the electrostatic repulsion, rising as Z2 due to its long–range nature, begins to dominate the strong interaction, which is only rising as A due to its short–range nature. The mean binding energy per nucleon falls gradually and the nuclei become less and less stable, until at Z = 83, A = 209 it is the ‘end of the road’ for long–term nuclear stability.
The constant binding energy per nucleon seen in the middle of Figure 4 is reminiscent of one of the properties of a liquid. For a liquid, such as water, we define the latent_heatlatent heat of vaporization to be the energy required to turn a given mass of liquid water into steam – that is, to dismantle the structure of the liquid and disperse the molecules as separate units. This is clearly analogous to the unbinding of the nucleus into separate nucleons. Latent heat is usually defined per unit mass (1 kg) but we could equally well give its value per molecule (although this would be inconvenient for the liquid case because of the very large numbers of molecules involved in a unit mass of 1 kg). Nevertheless, the important point is that in both the nucleus and the liquid the required investment of energy to dismantle the structure rises in proportion to the number of ‘particles’ (nucleons or molecules) involved. Moreover, the underlying cause of this similarity is the same in both cases; the attractive forces that hold the structure together are effectively short range. The force that attracts molecules together to allow liquefaction is called the van der Waals force and is effective only over separations of about 10−9 m. i The strong nuclear interaction is also short-range, though on a nuclear scale (~10−14 m). The similarity between the liquid and the nucleus is quite striking and can be pursued further than we are able to do here. i
4 Unstable nuclei
We will look briefly in this section at the properties of unstable nuclei. By this we mean nuclei which, after a characteristic time, split up into fragments so that the original nucleus no longer exists. This process is called radioactive decay i and any nucleus that exhibits radioactive decay is called a radioactive nucleus; some of these nuclei are represented as open circles on Figure 4. We will apply some of the results and concepts discussed in Sections 2 and 3 to this process, in particular Einstein’s equation.
4.1 A second look at Einstein’s equation
When we introduced Einstein’s equation E = mc2 in Subsection 3.2 we were dealing with particles that were at rest relative to their observer. The binding energy was defined hypothetically as the energy necessary to just break up (i.e. unbind) the stationary nucleus into its free constituents (protons and neutrons), which meant that the resultant constituents would have no kinetic energy. But when a radioactive nucleus at rest decays, the fragments always do have kinetic energy relative to the original nucleus. What difference does this make to the use of Einstein’s equation?
Einstein’s equation remains true, even when a particle has kinetic energy, but great care is needed in using it. It is certainly the case, confirmed by many experiments, that as the energy of a particle increases, so does its mass. For example, it becomes harder to accelerate a particle as its energy grows, just as you would expect for a particle of growing mass. However, nuclear physics would become almost impossible to discuss if we had to keep changing the masses of particles according to their speed. In order to avoid this, the masses that nuclear physicists refer to and use in their calculations are defined in a very precise way.
When we look up tables of masses, for instance Table 1, we are looking at what is known as the rest mass m0 of the atom or nucleus. This is defined to be the mass determined when the particle is at rest relative to the observer who measures it. So, no matter how fast a particle may be moving, the rest mass used to characterize it remains constant. It is implicit in all mass tables that it is the rest mass that is tabulated. The energy of a particle at rest or its rest mass energy is often called its rest energy E0 – defined by Einstein’s equation as E0 = m0c2. The energies we considered in the previous section were all rest energies. Thus, in the absence of any potential energy, the total energy, E, of any nucleus will be the sum of its rest energy E0 and its kinetic energy Ekin:
total energyE = E0 + Ekin = m0c2 + Ekin
andEkin = E − E0(3)
Now, Einstein showed, as part of his special theory of relativity, that when a particle of rest mass m0 travels at speed υ its total energy is
$E = \dfrac{m_0}{\sqrt{1-\upsilon^2/c^2}}$
So, it follows from Equation 3 that the kinetic energy of such a particle is given by
$E_{\rm kin} = E - E_0 = m_0c^2\left(\dfrac{1}{\sqrt{1-\upsilon^2/c^2}} - 1\right)$
In nuclear physics we must adopt this way of calculating kinetic energy. The familiar expression, $E_{\rm kin} = \frac12m_0\upsilon^2$, is true as an approximation only for particles with a kinetic energy very much smaller than their rest energy. (This is equivalent to saying that their speeds υ must be much less than c.) i Einstein’s equation and the above boxed expressions apply to all particles, regardless of their energy. This method of finding kinetic energy has the added advantage of being very straightforward. For example, if we are told that a proton has a total energy of 1 GeV (i.e. 1000 MeV) i then, since we know (from Subsection 3.2) that its rest energy is 938 MeV, it must have a kinetic energy of 62 MeV.
4.2 Some examples of unstable nuclei
The discovery of the existence of the first unstable nucleus is an interesting story. In 1896 Henri Becquerel (1852–1908) was studying the properties of the element uranium. He found that photographic plates in the vicinity of his experiments became fogged, even though they were carefully protected from light. He might have thrown the plates away as defective and thought no more about it. But he was a careful investigator who followed up this unexplained result and identified the source of the fogging as some emission from the uranium.
Since Becquerel’s time many unstable nuclei have been discovered and many have been manufactured. Table 2 shows a list of some unstable nuclides, in a format similar to that of Table 1 for the stable nuclides. Table 2 differs from Table 1 in the addition of the right–hand column, headed half–life. Half–life is a measure of how quickly a radioactive material decays. For example, if a sample has a half–life of 10 minutes, after this time half of the initial number of radioactive nuclei will have decayed. i
You will see, even from the few examples in Table 2, that the range of values of half–life is enormous: from milliseconds for 21886Rn to 2 × 1015 yr for 18676Os. The very large half–life of 18676Os or 23892U shows why we have used the term completely stable in the context of Figure 3. Even over a span of years a sample of osmium or uranium might appear to be stable because the decay rate is so low.
Nevertheless, it was the emissions from such decays from uranium that fogged Becquerel’s photographic plates and without this experimental evidence of decay, its occurrence might have gone unnoticed. The half–lives of the two isotopes of uranium, 23892U and 23592U, are so long that they have quoted relative abundances, just as if they were stable isotopes.
4.3 Conservation principles in decays
We shall now consider the decay of an unstable nucleus. i What will it decay into? Will any of the mass energy locked up in the nucleus be released? How much will be released? We will aim to solve these questions using only measured (rest) masses, Einstein’s equation and three basic conservation principles:
- 1
-
The conservation_of_chargeprinciple of charge conservation: The total electric charge after a decay is the same as the total charge beforehand.
- 2
-
The nucleonprinciple of nucleon number conservation: The total number of nucleons remains the same throughout the decay. i
- 3
-
The conservation_of_relativistic_energyprinciple of (relativistic) energy conservation: The energy of a nucleus before it decays is equal to the energy shared by the particles that it decays into. If the nucleus is at rest before the decay its energy will consist entirely of rest energy, but its energy after the decay will include the kinetic energy of the decay products as well as their rest energies.
Let us illustrate the first two principles with an example.
The unstable nucleus of radium, 22288Ra, is observed to decay into a radon nucleus, 21886Ra, and a helium nucleus, 42He. For historical reasons a 42He nucleus ejected in radioactive decay is called an alpha_particleα–particle. The decay reaction will be written:
22288Ra → 21886Ra + 42He
The number of protons in the radium nucleus is equal to its atomic number, 88. The right–hand side of the decay equation shows that these protons are shared by the two product nuclei, 86 in the radon nucleus and 2 in the helium nucleus. Therefore the number of protons is conserved in this process, and since protons are the only charged particles involved there is a total charge of 88e both before and after the decay. It follows that charge is conserved in the decay. The equation also shows that the mass number is conserved: 222 = 218 + 4. The mass number is equal to the total number of nucleons (i.e. neutrons and protons) in the nucleus. So nucleon number is also conserved in the decay. So you can see the first two principles of conservation are observed by this decay process. i Question T9 asks you to use these two conservation principles to deduce the products of a radioactive decay.
Question T9
A stationary nucleus of thorium 23090Th undergoes decay into a nucleus of radium Ra and an α particle. What is the equation of the decay?
Answer T9
The decay may be written:
23090Th → AZRa + 42He
Equating the number of protons on each side gives 90 = Z + 2 and equating the total number of nucleons on each side gives 230 = A + 4. Thus the reaction is:
23090Th → 22688Ra + 42He
(Z = 88 confirms that the decay–product nucleus is indeed radium.)
To see how the third principle, the conservation of relativistic energy is applied, we return to our earlier example and look at the energy associated with the 23090Ra decay. Tables 1 and Table_22 give the following atomic rest masses:
- mass of 22288Ra = 222.015 35 u
- mass of 21886Ra = 218.005 580 u
- mass of 42He = 4.002 603 u
The total rest mass of the decay fragments is therefore 218.005 580 u + 4.002 603 u = 222.008 183 u.
This is less than the rest mass of the radium nucleus. So the energy that this represents, using Einstein’s equation, is only part of the energy available from the rest energy of the radium nucleus. The energy left over – the equivalent of 0.007 170 u – appears as kinetic energy shared between the two product nuclei. i
We express the energy balance by writing the equation:
22288Ra → 21886Ra + 42He + Q
where the symbol Q stands for the kinetic energy available to the products.
The kinetic energy available in a decay is commonly called the Q–value of the decay. It is given (using rest masses) as:
Q = (mass of nucleus − sum of masses of decay fragments) × c2(4)
If we use masses in units of MeV/c2 then Q may readily be expressed in units of MeV. So in our particular example, using the answer to Question T7 that 1 u = 931.502 MeV/c2, we have Q = 0.007 170 × 931.502 (MeV/c2) × c2 = 6.679 MeV. The full equation of the decay is:
22288Ra → 21886Ra + 42He + 6.679 MeV
| Z | Element | Symbol | A | Atomic mass/u | Relative abundance/% |
Half-life |
|---|---|---|---|---|---|---|
| 1 | hydrogen | H | 1 | 1.007 825 | 99.985 | |
| 2 | 3.016 050 | 0.015 | ||||
| 2 | helium | He | 4 | 4.002 603 | 99.999 | |
| 88 | radium | Ra | 222 | 222.015 353 | 38 s | |
| 226 | 226.025 406 | 1.6 × 103 yr | ||||
| 90 | thorium | Th | 230 | 230.033 131 | 8.0 × 104 yr | |
| 233 | 233.041 579 | 22.3 min | ||||
| 92 | uranium | U | 235 | 235.043 925 | 0.72 | 7.04 × 108 yr |
| 238 | 238.050 786 | 99.28 | 4.47 × 109 yr |
Question T10
Using the data in the table, work out the Q–value and hence write down a full equation i for the decay of thorium 23090Th, that was the subject of Question T9,
23090Th → 22688Ra + 42He
Answer T10
From the answer to Question T9, the equation is
23090Th → 22688Ra + 42He
From Equation 4,
Q = (mass of nucleus − sum of masses of decay fragments) × c2(Eqn 4)
the additional data in the table gives the mass–equivalent of the Q–value of:
230.033 131 u − (226.025 406 + 4.002 603) u = 0.005 122 u
This means that Q = 0.005 122 u × 931.502 MeV/u = 4.771 MeV. The decay equation is therefore
23090Th → 22688Ra + 42He + 4.771 MeV
Forbidden decay
Finally we ask, are all decays possible which conserve the number of protons and neutrons? Or can we exclude some? Let us take our 22288Ra nucleus as an example again.
✦ Does the proposed decay 22288Ra → 22187Fr + 11H conserve the charge and the number of nucleons?
✧ By inspection, there are 88 (= 87 + 1) protons on each side and 222 (= 221 + 1) nucleons on each side. Therefore this decay would conserve both charge and the number of nucleons.
(Fr is the element francium.)
This new decay mode corresponds to the decay of 22288Ra with the loss of a proton (i.e. a hydrogen nucleus 11H). This might be an apparently reasonable decay to expect. But the energy balance tells a different story. The rest mass of 22288Ra is still 222.015 353 u but the rest mass of 22187Fr is 221.014 183 u and that of 11H is 1.007 825 u. Therefore, the Q–value (kinetic energy), as in Equation 4,
Q = (mass of nucleus − sum of masses of decay fragments) × c2(Eqn 4)
would be:
[222.015 353 − (221.014 183 + 1.007 825)] × 931.502 (MeV/c2) × c2 i
= −0.006 653 × 931.502 (MeV/c2) × c2 = −6.20 MeV
The answer is negative. There is not enough rest energy in the nucleus to provide the rest energies of the fragments let alone some extra kinetic energy. By the third principle stated above, this reaction is not permitted.
If Q < 0, the decay reaction cannot take place spontaneously.
We can now understand why α–decay is a favoured decay mode for a large nucleus when we remember the point made in Subsection 3.3, that the α–particle is itself an unusually stable entity with a relatively low energy. Its emission tends to leave energy available to produce a positive Q–value for the decay process.
| Z | Element | Symbol | A | Atomic mass/u | Relative abundance/% |
Half-life |
|---|---|---|---|---|---|---|
| 1 | hydrogen | H | 3 | 3.016 050 | 12.3 yr | |
| 2 | helium | He | 4 | 4.002 603 | 99.999 | |
| 4 | beryllium | Be | 8 | 8.0053 | ~3 × 10−16 s | |
| 6 | carbon | C | 14 | 14.003 242 | 57301 yr | |
| 19 | potassium | K | 40 | 39.963 999 | 0.01 | 1.28 × 109 yr |
| 53 | iodine | I | 131 | 130.906 119 | 8.04 days | |
| 76 | osmium | Os | 186 | 185.953 852 | 1.6 | 2 × 1015 yr |
| 78 | platinum | Pt | 190 | 189.959 937 | 0.013 | 6 × 1011 yr |
| 84 | polonium | Po | 218 | 218.008 930 | 3.05 min | |
| 86 | radon | Rn | 218 | 218.005 580 | 0.035 s | |
| 222 | 222.017 574 | 3.82 days | ||||
| 87 | francium | Fr | 221 | 221.014 183 | 4.8 min |
Question T11
From the data in the table determine whether the decay
19078Pt → 18676Os + 42He
is possible.
Answer T11
The mass–equivalent of the Q–value is equal to:
189.959 937 u − (185.953 852 + 4.002 603) u = 0.003 482 u
This is positive, so the decay is energetically possible.
5 Closing items
5.1 Module summary
- 1
-
Each atom has a nucleus – a positively charged ‘core’ that has a diameter of approximately 10−14 m. Apart from the hydrogen nucleus 11H, which is a proton, nuclei in general consist of combinations of protons and neutrons.
- 2
-
Each nucleus is characterized by its atomic number Z which gives the number of protons in the nucleus and its mass number A which gives the total number of nucleons (neutrons and protons) in the nucleus. Different isotopes of an element have different mass numbers but the same atomic number.
- 3
-
Nucleons are bound together in the nucleus by the strong interaction, which acts between all nucleons, is attractive, and has a range of about 10−14 m.
- 4
-
Energy has a mass equivalent. The mass m that is equivalent to energy E is given by Einstein’s equation
E = mc2(Eqn 1)
where c is the speed of light.
- 5
-
Nuclear energies are conveniently measured in units of MeV (megaelectronvolts)
- 6
-
Nuclear masses are conveniently measured in atomic mass units (u) or in MeV/c2, where c is the speed of light.
- 7
-
The mass of a stable nucleus that contains more than one constituent is less than the sum of the masses of its free constituents. The difference is called the nuclear binding energy, and this may be calculated from measured values of nuclear masses.
- 8
-
The binding energy per constituent nucleon is, over a substantial range of nuclei, approximately constant at about 8.5 MeV. Very light and very heavy nuclei have smaller binding energies per nucleon.
- 9
-
The shape of the nuclear binding energy graph is consistent with the characteristics of the strong interaction between nucleons.
- 10
-
Not all nuclei are stable. Radioactive nuclei are unstable; they undergo radioactive decay. The half–life is the characteristic time after which half an original sample of radioactive nuclei can be expected to have decayed. There is an enormous range in values of half-life for radioactive nuclei.
- 11
-
The total (relativistic) energy of a particle is equal to its rest energy plus its kinetic energy. Tables of atomic masses are tables of rest mass.
- 12
-
Charge, nucleon number and (relativistic) energy are conserved in radioactive decay processes.
- 13
-
Mass tables can be used to calculate the kinetic energy of the decay products and to determine whether a reaction will be permitted by energy conservation.
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Describe the contents of a nucleus denoted in the standard way.
- A3
-
Explain why nuclei generally have more neutrons than protons.
- A4
-
Use Einstein’s equation to calculate the rest energy of a particle given its mass in kg, with the answer given in units of J or MeV/c2.
- A5
-
Calculate the mass defect (in units of u and MeV/c2) of a nucleus using mass tables and the conversion factor from u to MeV/c2.
- A6
-
Calculate the binding energy of a nucleus in MeV using mass tables and the conversion factor from u to MeV/c2.
- A7
-
Write down an appropriate α–decay equation, and decide whether a given α–decay equation is plausible.
- A8
-
Calculate the Q–value of a given α–decay and hence decide whether the decay is energetically possible.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A2)
The nucleus 2713Al has an atomic mass of 26.981 541 u.
(a) How many protons does the nucleus contain?
(b) How many neutrons does the nucleus contain?
(c) By what factor is 2713Al more massive than 126C?
Answer E1
(a) From the notation, 2713Al has 13 protons.
(b) The nucleus contains 27 nucleons in total, and so it has 14 neutrons.
(c) By definition 126C has a mass of precisely 12 u. The ratio of the masses is therefore (26.981 541 u)/12 u = 2.248 4618.
(Reread Subsection 2.1 if you had difficulty with this question.)
Question E2 (A3)
All nuclei with large Z have more neutrons than protons. Explain in terms of the interactions concerned why this might be so.
Answer E2
There are two main interactions between nucleons in the nucleus. The strong interaction is attractive but of very short range. It acts between both neutrons and protons but, because of its short range, its contribution increases only in proportion to the total number of nucleons A. The electrostatic interaction acts only between the protons in the nucleus and is repulsive. Because the electrostatic interaction is long range, it increases in proportion to the number of pairs of protons and so increases approximately in proportion to Z2. As Z become larger the Z2 dependence of the electrostatic repulsion has to be counteracted by ‘strong interaction’ attraction from more and more nucleons.
(Reread Subsections 2.2 and 3.3 if you had difficulty with this question.)
Question E3 (A4)
The (rest) mass of the neutron is 1.675 × 10−27 kg. Use the Einstein equation to calculate its rest energy. Give your answer in J and in MeV.
(Use c = 2.998 × 108 m s−1)
Answer E3
For m = 1.675 × 10−27 kg, E = mc2 = 1.675 × 10−27 kg × 8.9880 × 1016 m2 s−2 = 1.5055 × 10−10 J.
Since 1 eV = 1.602 × 10−19 J, the rest energy of the neutron is 939.8 MeV.
(Reread Subsection 3.2 if you had difficulty with this question.)
| Z | Element | Symbol | A | Atomic mass/u | Relative abundance/% |
|---|---|---|---|---|---|
| 1 | hydrogen | H | 1 | 1.007 825 | 99.985 |
| 30 | zinc | Zn | 64 | 63.929 145 | 48.6 |
| 66 | 65.926 035 | 27.9 | |||
| 67 | 66.927 129 | 4.1 | |||
| 68 | 67.924 846 | 18.8 | |||
| 70 | 69.925 325 | 0.6 | |||
| 79 | gold | Au | 197 | 196.966 560 | 100 |
| 82 | lead | Pb | 204 | 203.973 037 | 1.4 |
| 206 | 205.974 455 | 24.1 | |||
| 207 | 206.975 885 | 22.1 | |||
| 208 | 207.976 641 | 52.4 | |||
| 83 | bismuth | Bi | 209 | 208.980 388 | 100 |
Question E4 (A5 and A6)
Using data from the table calculate:
(a) The mass defect of the nucleus of 19779A in u, 79 MeV/c2 and GeV/c2.
(b) The binding energy of the nucleus of 19779Au in GeV.
(1 u = 931.502 MeV/c2 and Au is the chemical symbol for gold)
Answer E4
(a) From the table the mass defect for 19779Au is:
79 × 1.007 825 u + 118 × 1.008 665 u − 196.966 560 u = 1.674 085 u.
Using 1 u = 931.502 MeV/c2, the mass defect for 19779Au is 1559.46 MeV/c2, which can be written as 1.559 46 GeV/c2.
(b) The binding energy of 19779Au is, therefore, 1.559 461GeV.
(Reread Subsections 3.1 and 3.2 if you had difficulty with this question.)
| Z | Element | Symbol | A | Atomic mass/u | Relative abundance/% |
Half-life |
|---|---|---|---|---|---|---|
| 1 | hydrogen | H | 3 | 3.016 050 | 12.3 yr | |
| 2 | helium | He | 4 | 4.002 603 | 99.999 | |
| 4 | beryllium | Be | 8 | 8.0053 | ~3 × 10−16 s | |
| 6 | carbon | C | 14 | 14.003 242 | 57301 yr | |
| 19 | potassium | K | 40 | 39.963 999 | 0.01 | 1.28 × 109 yr |
| 53 | iodine | I | 131 | 130.906 119 | 8.04 days | |
| 76 | osmium | Os | 186 | 185.953 852 | 1.6 | 2 × 1015 yr |
| 78 | platinum | Pt | 190 | 189.959 937 | 0.013 | 6 × 1011 yr |
| 84 | polonium | Po | 218 | 218.008 930 | 3.05 min | |
| 86 | radon | Rn | 218 | 218.005 580 | 0.035 s | |
| 222 | 222.017 574 | 3.82 days | ||||
| 87 | francium | Fr | 221 | 221.014 183 | 4.8 min |
Question E5 (A7 and A8)
A nucleus of radon 22286Rn decays into a nucleus of polonium (Po) and an α–particle.
(a) Write down the equation of the decay.
(b) Calculate the Q–value for the decay, using data from the table, and hence complete the decay equation.
(1 u = 931.502 MeV/c2)
Answer E5
(a) In order that the total A and Z values are the same on both sides of the decay equation, this must be:
22286Rn → 21884Po + 42He
(b) The table gives the mass–equivalent of the Q–value:
222.017 574 − (218.008 607 + 4.002 603) u = 0.006 364 u = 5.928 MeV/c2
The complete equation of the decay is, therefore:
22286Rn → 21884Po + 42He + 5.928 MeV
(Reread Subsections 4.1 and 4.3 if you had difficulty with this question.)
| Z | Element | Symbol | A | Atomic mass/u | Relative abundance/% |
Half-life |
|---|---|---|---|---|---|---|
| 1 | hydrogen | H | 1 | 1.007 825 | 99.985 | |
| 2 | 3.016 050 | 0.015 | ||||
| 2 | helium | He | 4 | 4.002 603 | 99.999 | |
| 87 | francium | Fr | 221 | 221.014 183 | 4.8 min | |
| 88 | radium | Ra | 222 | 222.015 353 | 38 s | |
| 226 | 226.025 406 | 1.6 × 103 yr | ||||
| 90 | thorium | Th | 230 | 230.033 131 | 8.0 × 104 yr | |
| 233 | 233.041 579 | 22.3 min | ||||
| 92 | uranium | U | 235 | 235.043 925 | 0.72 | 7.04 × 108 yr |
| 238 | 238.050 786 | 99.28 | 4.47 × 109 yr |
Question E6 (A7 and A8)
For each of the following decays, decide whether it is forbidden (use data from the table) and give a reason for your decision:
(a) 22688Ra → 22387Fr + 11H
(b) 23592U → 23090Th + 42He + 10n
Answer E6
(a) 22688Ra → 22387Fr + 11He
Although the number of protons on each side is the same (88 = 87 + 1), the total number of nucleons is not (226 ≠ 223 + 1). This does not conserve the number of nucleons. Therefore this decay cannot take place.
(b) 23592U → 23090Th + 42He + 10n
Both the number of protons (92 = 90 + 2) and the number of nucleons (235 = 230 + 4 + 1) are conserved in this proposed decay. However, from the table the rest mass of 23592U (on the left–hand side) is 235.043 925 u whereas the sum of the rest masses of the nuclei on the right–hand side is:
(230.033 131 + 4.002 603 + 1.008 665) u = 235.044 399 u
The mass equivalent of the Q–value would be −0.000474 u. The reaction, although satisfying the nucleon conservation criterion, cannot satisfy energy conservation for the particles considered. (There is not enough rest energy in the uranium nucleus to supply the rest energies of the thorium nucleus, the α–particle and the neutron.)
Note Although we have used atomic masses rather than nuclear masses in this calculation, the final answer is correct. The overestimates arising from the inclusion of electron masses cancel when the masses are subtracted.
(Reread Subsections 4.1 and 4.3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.