PHYS 5.1: Simple harmonic motion |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Vibrations and oscillations are part of your everyday life. Within minutes of waking up, you may well experience vibrations in a wide variety of forms: the buzzing of the alarm clock; the bounce of your bed; the oscillations of a loudspeaker, which in turn are produced by oscillations of charges in electric circuits; the vibrations of an electric toothbrush or an electric razor, and so on. Some are very welcome and aesthetically pleasing, such as the vibrations of musical instruments. Others, such as the vibrations caused by machinery and traffic, are noisy and annoying. Vibrations range from the small–scale motions of atoms in solids to the large–scale swaying of bridges and tall buildings; from the irregular bending of a tree in the wind to the extremely regular oscillations of the balance wheel of a watch. A common feature of many of these vibrations or oscillations is that the motion is repetitive or periodic. Such motions are described as periodic motions and the shortest time over which the motion repeats is called the period or periodic time.
This module is concerned with one of the simplest types of periodic motion – simple harmonic motion (SHM). In SHM the displacement, velocity and acceleration of the oscillating object can all be represented as sinusoidal functions of time.
SHM arises whenever an object is made to oscillate about a position of equilibrium by a force that has the following characteristics:
- the force is always directed towards the position of equilibrium;
- the force has a magnitude which is proportional to the distance between the object and the position of equilibrium.
In practice, when most stable systems are displaced slightly from equilibrium and then released, the periodic motion that follows can be treated as SHM, a combination of SHMs, or at least an approximation to one or more SHMs. For this reason SHM can be regarded as a basic building block of far more complicated periodic motions.
The simple mechanics of SHM (along with a mathematical model of SHM and its phasor representation) are discussed in Section 2. The more complicated (but realistic) oscillations that occur in more than one dimension are covered in Section 3, where the superposition of SHMs is discussed.
In nature a vast range of different systems exhibit SHM. In this module we will be concerned mainly with oscillations in mechanical systems. There are many analogous oscillations of electrical or electronic systems but these are described elsewhere in FLAP.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 4.1Module summary and the Subsection 4.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 4.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
A stable system, if slightly disturbed, oscillates about its position of equilibrium. Explain why it does this, with reference to a simple pendulum.
Answer F1
At positions close to equilibrium, the pendulum bob is subject to a restoring force which tends to return it to the position of equilibrium. When it is moving towards the position of equilibrium it accelerates under the action of the force. When it is moving away, the force slows it and brings it to rest, whereupon it once more moves towards the position of equilibrium.
Question F2
A body of mass m oscillates with SHM in one dimension about a position of equilibrium (x = 0) and has a frequency f, angular frequency ω and amplitude A. The displacement from the position of equilibrium is x, and this displacement is A at t = 0. Write down an expression for the displacement of the body from equilibrium at time t and derive expressions for the velocity, acceleration and the force acting at this same time. Write down an expression giving the force in terms of m, x and ω.
Answer F2
One expression for the displacement is
x (t) = A cos(ωt + ϕ) (here ϕ = 0)(Eqn 6a)
and by differentiation with respect to time this leads to
υx(t) = −Aω sin(ωt + ϕ)(Eqn 9a)
andax(t) = −Aω2 cos(ωt + ϕ)(Eqn 10a)
andax(t) = −ω2x (t)(Eqn 12)
Using F = ma and Equation 12 we arrive at
Fx(t) = −mω2x (t)(Eqn 13)
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with the following terms: acceleration, angular speed, Cartesian coordinates, deceleration, displacement, distance–time graph, equilibrium, force, mass, Newton’s laws of motion, speed, uniform circular motion, velocity, velocity–time graph, weight and the mathematical concepts of angle, circle, degree, ellipse, gradient, inverse trigonometric functions (in particular, arctanarctan x), magnitude_of_a_real_quantitymagnitude, local_maximamaxima and local_minimaminima, modulus, parabola, periodic function, radian, tangent_to_a_curvetangent, trigonometric functions, vector, vector addition, components_of_a_vectorvector component. You do not need to be fully conversant with differentiation in order to study this module, but you should be familiar with the calculus notation dx/dt used to represent the rate of change of x with respect to t (i.e. the derivative of x with respect to t). If you are unsure about any of these terms you should refer to the Glossary, which will also indicate where in FLAP they are developed. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
Are any of the following functions periodic_functionperiodic and, if so, what is their period? (a) sin x, (b) cos2 x, (c) x3 − 3x2 + 3x − 1.
Answer R1
A function f (x) is said to be periodic_functionperiodic with period a if f (x) = f (x + a) for all values of x. (a) This function is periodic with a period 2π. (b) This function is periodic with a period π (draw its graph if you don’t see why). (c) This function is not periodic.
Question R2
Express the following angles in radians: (a) 30°, (b) 135°.
Answer R2
(a) $30° = \rm \dfrac{\pi}{6}\,radians$, (b) $135° = \rm\dfrac{3\pi}{4}\,radians$.
Question R3
Give the values of t within the range t = 0 to t = 1 at which each of the following periodic_functionperiodic functions has a maximum, a minimum, and a zero. (a) cos 2πt, (b) sin 2πt, (c) cos 4πt, (d) cos(2πt + π/2).
Answer R3
The values of t within the range t = 0 to t = 1 at which the function is (i) a localmaximamaximum; (ii) a localminimaminimum; or (iii) zero are as follows:
(a) (i) 0, 1; (ii) 0.5; (iii) 0.25, 0.75
(b) (i) 0.25; (ii) 0.75; (iii) 0, 0.5, 1
(c) (i) 0, 0.5, 1; (ii) 0.25, 0.75; (iii) 0.125, 0.375, 0.625, 0.875
(d) (i) 0.75; (ii) 0.25; (iii) 0, 0.5, 1
Question R4
If x = A cos(ωt + ϕ), where A, ω and ϕ are constants, what is the derivative dx/dt. (You may use graphical techniques if you are unfamiliar with differentiation.)
Answer R4
The derivative dx/dt = −ωA sin(ωt + ϕ).
Question R5
In two dimensions, the displacement vectors $\overrightarrow{OA}$ and $\overrightarrow{OB}$ are defined in terms of their components_of_a_vectorcomponents by $\overrightarrow{OA} = (1,2)$ and $\overrightarrow{OB} = (3,2)$. Using components write down expressions for their resultant $\overrightarrow{OC}$ and for the displacement $\overrightarrow{AB}$. What is the angle between $\overrightarrow{OC}$ and $\overrightarrow{AB}$?
Answer R5
$\overrightarrow{OC} = \overrightarrow{OA} + \overrightarrow{OB} = (4,4)$.
$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = (2,0)$.
The angle between \overrightarrow{OC}$ and $\overrightarrow{AB}$ is 45°.
Question R6
A train consists of a string of carriages of total mass 4.0 × 105 kg, coupled to a locomotive of mass 1.0 × 105 kg.
(a) What is the magnitude_of_a_vector_or_vector_quantitymagnitude of the weight of the entire train? What is the direction of the weight?
(b) If the train accelerates uniformly from rest on a straight level track to a velocity of 81 km h−1 due north, achieving this velocity in 6 min, what is its acceleration along the track?
(c) The train stops accelerating, and maintains its velocity of 81 km h−1 due north for a further 12 min. It then decelerates uniformly until it stops at the next station, which it reaches in a further 12 min. Sketch the velocity–time graph of the train and calculate the total distance travelled over the full 30 min.
(d) During the acceleration, what is the net horizontal force acting on the locomotive? What is the net horizontal force acting on the carriages?
Answer R6
(a) If the magnitude of the acceleration due to gravity is 9.8 m s−1, the magnitude_of_a_vector_or_vector_quantitymagnitude of the weight is
W = mg = 5.0 × 105 kg × 9.8 m s−1 = 4.9 × 106 N.
Weight is a vector quantity (a force) and acts downwards.
(b) Acceleration is a vector quantity equal to the rate of change of velocity. In this case it is directed due north (which we choose to be the x direction) and can be specified by the single components_of_a_vectorcomponent ax:
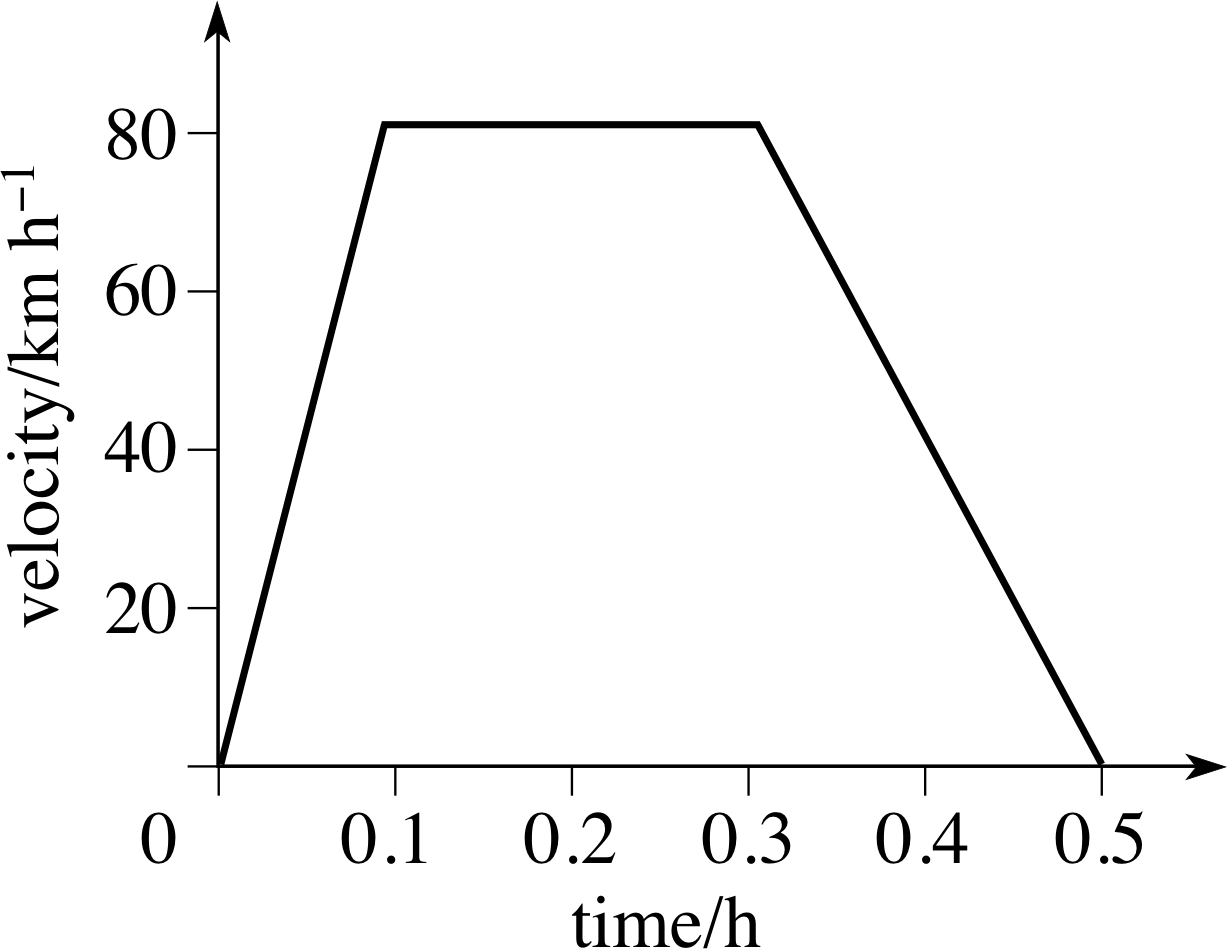
Figure 19 See Answer R6.
$a_x = \rm \dfrac{81\times1000\,m\,h^{-1}}{3600\,s\,h^{-1}\times6\,min\times60\,s\,min^{-1}} = 0.0625\,ms$
(c) The velocity–time graph is shown in Figure 19. The total distance is the area under the graph
$= \rm 81\left(\dfrac{0.1}{2} + 0. 2 + \dfrac{0.2}{2}\right)\,km = 28\,km$
(d) The required forces must both act in the x direction (i.e. due north) so they can both be specified by a single component Fx = max:
Fx = 1.0 × 105 kg × 0.0625 m s−2 = 6.25 × 103 N for the locomotive
and Fx = 4.0 × 105 kg × 0.0625 m s−2 = 2.5 × 104 N for the carriages
Comment If you had difficulty with any of these Ready to study questions, consult the Glossary for further information and references about the terms concerned.
2 Simple harmonic motion in one dimension
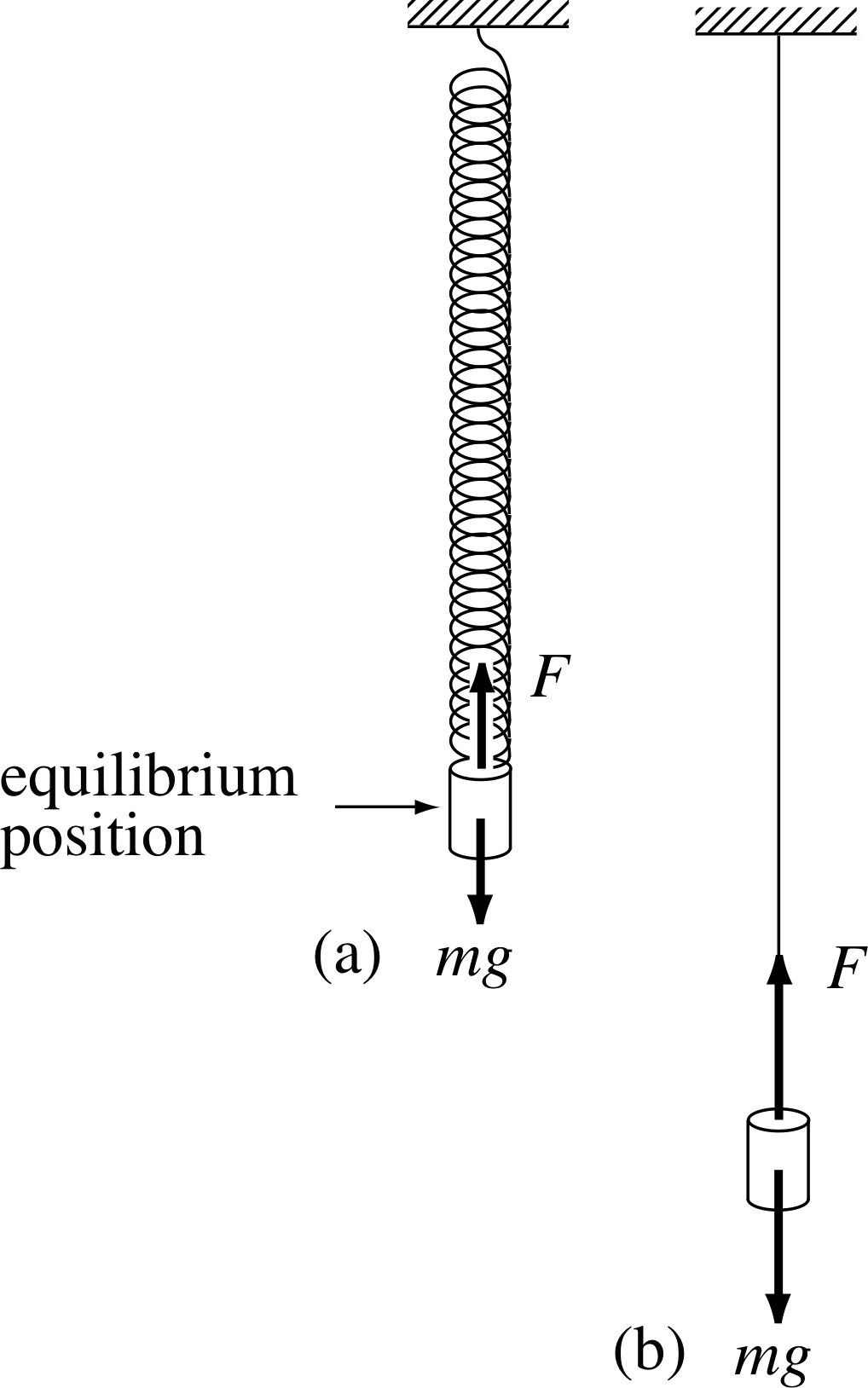
Figure 1 Two simple oscillators in their equilibrium positions.
2.1 Equilibrium conditions and simple oscillators
Consider the two mechanical systems illustrated in Figure 1. Figure 1a represents a body suspended from the end of a light coil spring i, and Figure 1b shows a similar body called a bob suspended from the end of a light thread (i.e. a pendulum). Both systems are in equilibrium, which is to say that there is no net force acting on any part of the system. i
✦ In each case, what forces are acting on the body of mass m, and how are they related? What is the net force acting?
✧ Each body is acted upon by its own weight, of magnitude mg, directed vertically downwards through its centre of mass. This is opposed by the force F due to the spring tension in Figure 1a and the thread tension in Figure 1b. In each case, the force is equal in magnitude but opposite in direction to the weight, so there is no net force acting on either body.
Notice that in each of the two systems, there is a unique position of equilibrium. In Figure 1a the spring force increases with the extension and at the position of equilibrium the force is just sufficient to support the weight of the body. The same is true in Figure 1b, as the thread is stretched slightly by the weight of the bob and the tension and the weight are colinear i at the position of equilibrium. Also, note that if the body in Figure 1a is displaced vertically down from its position of equilibrium, and then released, it will oscillate up and down. In a similar way, if the bob in Figure 1b is moved a short distance to one side and released, it will oscillate from side to side. These observations tell us that these equilibrium positions are points of stable equilibrium, in which a small displacement from the position of equilibrium causes forces which tend to restore the system to its position of equilibrium. i
In contrast, a system in unstable equilibrium would, if disturbed, move away from the position of equilibrium. An example of such a system would be a small ball placed on top of a larger sphere. A system lacking any tendency either to return to or move further from its position of equilibrium is said to be in neutral equilibrium. An example here would be a small ball on a flat surface.
It is clear that oscillations about a position of equilibrium are possible only in the case of a position of stable equilibrium. Both systems in Figure 1 are in stable equilibrium. If the thread in Figure 1b were replaced by a light, rigid rod, supported at its upper end so that it is able to turn full-circle, there would be a position of unstable equilibrium with the centre of mass of the bob carefully balanced vertically above the point of support.
✦ How could the situations depicted in Figure 1b be turned into ones of neutral equilibrium?
✧ If the experiments of Figure 1b were conducted in deep space, away from the gravitational influence of the Earth or any other body, then there would be neutral equilibrium for any position of the mass.
Think about the oscillations of a stable system and try to answer the following questions before continuing. If you find it helps, hang up a pendulum and watch it swing.
✦ When the body is displaced from its equilibrium position and then released from rest, in what direction does it initially move with respect to the position of equilibrium?
What does your answer tell you about the net force on the body when it is displaced from equilibrium?
In the oscillation, is the maximum distance reached the same on each side of the position of equilibrium?
What is the speed of the body when at its maximum distance from the position of equilibrium?
Is the speed of the body constant as it moves between positions of maximum displacement?
If not, where is the speed greatest?
Is the motion of the body when it is moving in one direction similar to that when it is moving in the opposite direction?
✧ If it is released from rest, the body will move initially towards the position of equilibrium. This implies that the net force acting on it is in this same direction, and for this reason (i.e. because it tends to restore equilibrium) is often referred to as the restoring force. The oscillations occur between two turning points, one on either side of the position of equilibrium and equidistant from it (providing there are no energy losses from the system). At each turning point the speed is zero. On leaving a turning point, the body accelerates smoothly towards the position of equilibrium, where it reaches its maximum speed, then decelerates smoothly as it approaches the other turning point.
The motion is completely symmetric with respect to the position of equilibrium.
What we have just described qualitatively is known as simple harmonic motion, usually abbreviated to SHM. This type of motion can be defined kinematicskinematically, through a description of the motion of the body, or dynamicsdynamically in terms of the force which acts on the body to produce the observed motion. In this section, we will adopt the former approach first, then show that the two are equivalent. In addition to the swinging pendulum or vibrating mass on a spring there are a great many practical situations in which the motion can be described to a good approximation as SHM – for example, a boat pitching and tossing or just bobbing on the water, a car bouncing on its suspension, a vibrating string on a musical instrument, the air in an organ pipe or the motion of water in a ship’s wake. We will now develop a common way of representing such motions.
2.2 Mathematical representations of SHM
The key features of SHM are that the motion is repetitive or periodic and that it involves a maximum displacement from the position of equilibrium. These features must appear in any mathematical representation of SHM.
The magnitude of the maximum displacement from equilibrium is called the amplitude A of the motion. As a magnitude, the amplitude cannot be negative. The time over which the motion repeats is called the period or periodperiodic time T and this can be measured from any point in the motion to the next equivalent point. One full period is just sufficient for one complete cycle or oscillation of the motion, from a turning point, say, through the position of equilibrium to the other turning point and back again to the original turning point. i The frequency f is the number of cycles completed in one second and is the reciprocal of the period (measured in seconds):
$f = \dfrac1T$(1)
The units of frequency are used so often and so widely that they have been given the special name hertz, which may be abbreviated to Hz. Thus
1 hertz = 1 Hz = 1 second−1 = 1 s−1 i
If the moving object travels backwards and forwards along a straight line (as in Figure 1a) we say the motion is linear and refer to it as one–dimensional SHM. i In such cases we can take the position of equilibrium to be the origin of a Cartesian coordinate system and by choosing the orientation of the system appropriately we can represent the displacement from equilibrium, measured along the line of motion, by the position coordinate x.
To represent the variation of displacement with time mathematically we require x as a periodic function of time t. The simplest periodic functions to use are sine and cosine, so we could, for example, represent a one–dimensional periodic motion, about the origin by i
$x(t) = A\cos\left(\dfrac{2\pi t}{T}\right)$(2a)
where A and T are constants, and x (t) denotes the displacement from the position of equilibrium at time t. As a first step towards confirming that Equation 2a represents the key features of SHM, answer the following question.
✦ What is the displacement at times t = 0, t = T, t = T/2, t = T/4 and t = 3T/4?
✧ At t = 0 the displacement of the body is x = A cos 0 = A;
at t = T, x = A cos 2π = A;
at t = T/2, x = A cos π = −A;
at t = T/4, x = A cos(π/2) = 0;
at t = 3T/4, x = A cos(3π/2) = 0.
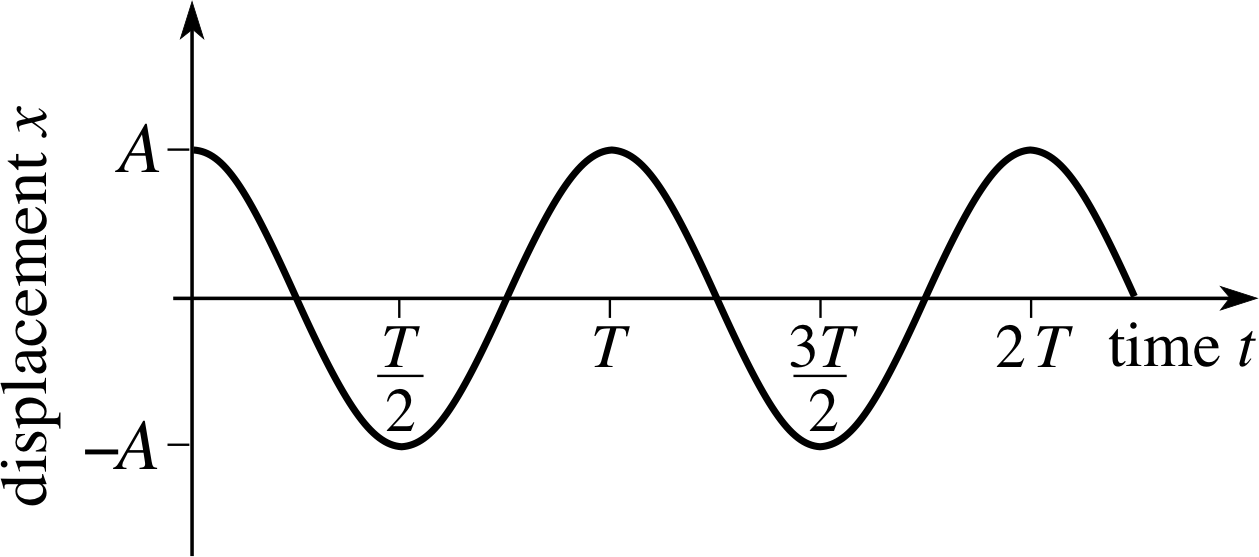
Figure 2 A displacement–time graph for SHM.
Figure 2 shows just over two cycles of this linear motion as a displacement–time graph. Examine this graph carefully, and notice that, in all essential details, it corresponds closely to the qualitative description of SHM given earlier. In particular, note that:
- The motion is periodic with periodic time T. If you compare the portion of Figure 2 from t = 0 to t = T with that from t = T to t = 2T, these portions are obviously identical. The graph thus repeats itself after a time T.
- It has a maximum displacement or amplitude A.
- It shows an object moving smoothly and symmetrically between two turning points. i
- It shows an object which is stationary at the turning points and which moves with a changing velocity υx between the turning points, attaining a maximum speed as it passes through the position of equilibrium at x = 0. i
- Since the velocity υx changes smoothly between the turning points the acceleration must also be changing smoothly over a cycle and, from Newton’s second law of motion Fx = max, this implies a smoothly varying force acting on the object.
In order to probe Equation 2a further, let us construct the corresponding velocity–time graph and accelerationacceleration–time graph of the motion. In order to establish that they also accord with our qualitative ideas of SHM.
Question T1
Using Figure 2, make a rough sketch of the velocity–time graph corresponding to Equation 2a over the interval 0 ≤ t ≤ 2T. Use your answer to help you sketch the acceleration–time graph over the same interval.
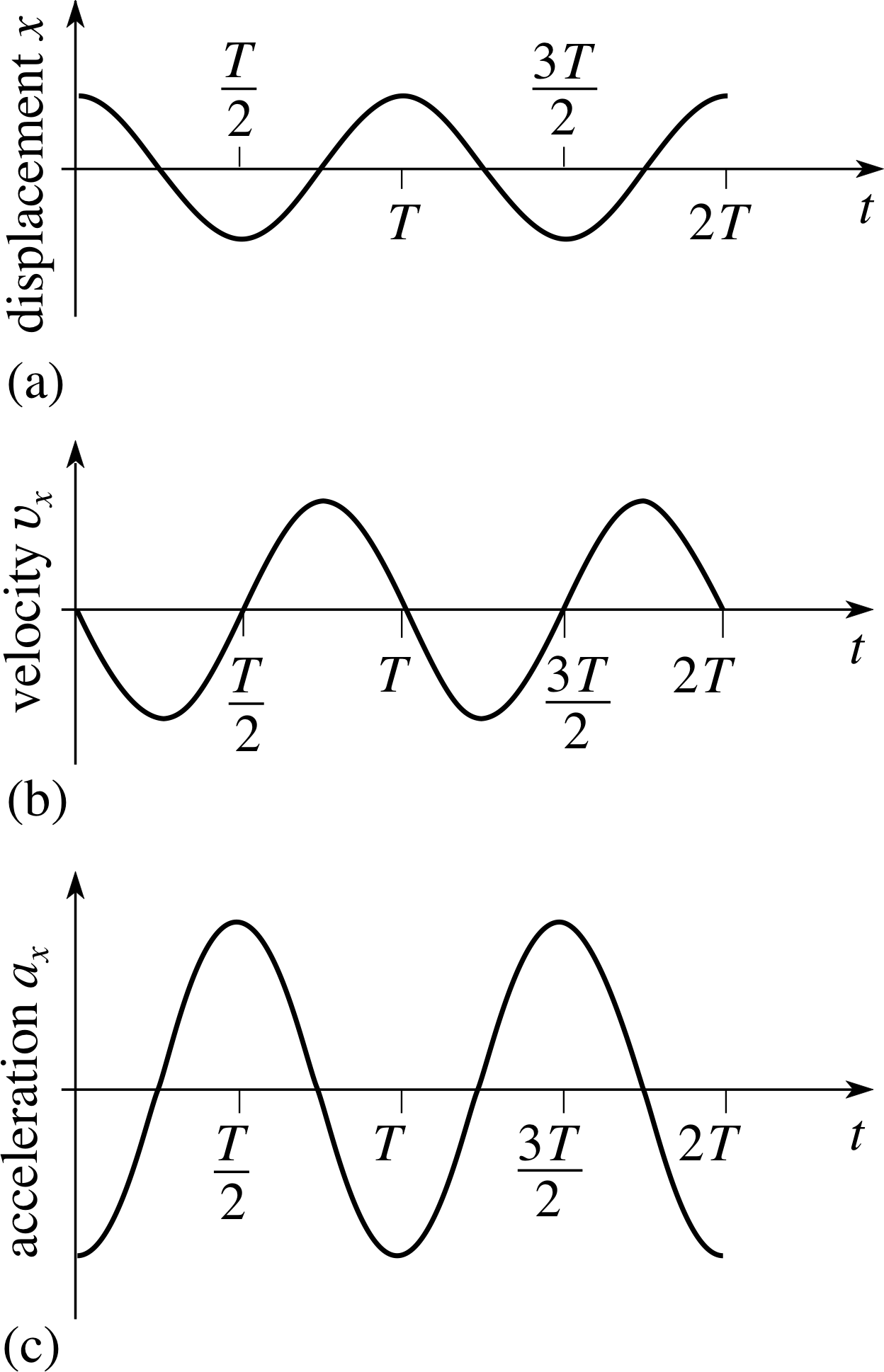
Figure 20 See Answer T1.
Answer T1
The velocity–time graph is given in Figure 20b and the acceleration–time graph in Figure 20c. The original displacement–time graph is shown for comparison in Figure 20a. Notice that the velocity initially goes negative.
Comment In one–dimensional motion along the x–axis, the velocity υx and acceleration ax are the x–components of vector quantities. Where there is no risk of ambiguity, we will continue to refer to them simply as velocity and acceleration, but in notation we will use υx and ax to signify their nature as components.
From Question T1 we see that Equation 2a produces all the aspects of SHM which we have so far identified. It is tempting to define SHM quantitatively by Equation 2a. However, before we jump to this conclusion we have to consider whether this would be sufficiently general to be a definition of SHM.
For example, Equation 2a insists that at time t = 0 the object has its maximum displacement of x = A and is at rest. Equation 2a cannot, for example, represent the situation in which we consider the same motion but we start our clock from t = 0 as the object passes through its position of equilibrium at x = 0. In this case we need x = 0 at t = 0 and the cosine function of Equation 2a does not satisfy this requirement.
✦ Suggest an alternative to Equation 2a that describes the same motion but allows us to have x = 0 at t = 0, and, also, where υx has its maximum value at t = 0.
✧ The solution is to replace the cosine function in Equation 2a,
$x(t) = A\cos\left(\dfrac{2\pi t}{T}\right)$(Eqn 2a)
by a sine function, which is zero at t = 0 and whose slope is greatest at t = 0.
The implication of this is that the expression
$x(t) = A\sin\left(\dfrac{2\pi t}{T}\right)$(2b)
is an equally valid representation of one–dimensional SHM, but under different initial conditions.
The sine and the cosine functions both have a common general shape that is usually described as sinusoidal, without stipulating whether it is the sine or the cosine function that is involved. It is this wavy sinusoidal shape that is the crucial feature of the kinematic definition of SHM.
The general mathematical representation of one–dimensional SHM must include Equations 2a and 2b as particular cases, but it must also include all those other sinusoidal functions which have neither a maximum nor a minimum at t = 0. Once we know this general mathematical representation we can be confident that if we observe an example of SHM and measure corresponding values for x and t then those data will fit the general mathematical representation for some appropriate choice of initial conditions. In other words, our general mathematical representation should be sufficiently general that we should be able to regard any given stage of the motion as corresponding to t = 0. Developing this general representation of one–dimensional SHM will occupy much of the next subsection, but first we must discuss a feature of Equations 2a and 2b that we have so far glossed over.
The form of Equations 2a and 2b implies that over each period of oscillation, as the time t increases its value by the fixed amount T, the oscillator passes through a complete cycle of x values. Now, during such a cycle, the quantity 2πt/T (i.e. the argument of the sine and cosine functions) increases by 2π, and each additional increment of 2π corresponds to another complete oscillation. In this way the argument of the sine or cosine function behaves rather like an angle measured in radians, since that too would complete an additional cycle for each increase of 2π radians (or 360°). Of course, there’s not really any angle involved here since the motion is linear and the quantity 2πt/T has no units; what the argument of the periodic sine or cosine function tells us is the stage that the moving particle has reached within its own cycle of oscillation. Nonetheless, the argument of the periodic function is often referred to as the phase angle or simply the phase of the motion and is as likely to be expressed in radians (or the corresponding number of degrees) as it is to be given as a unitless number. A phase of 0 corresponds to the start of a cycle, a phase of 2π to the start of the next cycle, 4π the next, and so on. If the motion is halfway through the first cycle the phase is π.
$x(t) = A\cos\left(\dfrac{2\pi t}{T}\right)$(2a)
$x(t) = A\sin\left(\dfrac{2\pi t}{T}\right)$(2b)
It is possible to write the phase in Equations 2a and 2bmore simply by introducing the angular frequency ω (Greek letter omega) as a shorthand for 2π/T so that 2πt/T = ωt. You will soon see some of the advantages of introducing ω but for the moment let’s just note that its value determines the rate of change of the phase, that the units of ω are s−1 and that it makes sense to call it angular frequency because it is related to the ordinary oscillation frequency and time period as follows:
$\omega = \dfrac{2\pi}{T} = 2\pi f$(3)
Hence,$T = \dfrac1f = \dfrac{2\pi}{\omega}$(4)
Finally, we note that in terms of angular frequency Equations 2a and 2b can be written as
x = A cos ωt(5a)
andx = A sin ωt(5b)
Question T2
Calculate the frequency and angular frequency for an oscillation of period 200 μs.
Answer T2
The period is T = 2 × 10−4 s so that from Equation 4,
Hence,$T = \dfrac1f = \dfrac{2\pi}{\omega}$(Eqn 4)
f = 1/T = 5 kHz, and from Equation 3,
$\omega = \dfrac{2\pi}{T} = 2\pi f$(Eqn 3)
the angular frequency is ω = 2πf = π × 104 s−1.
2.3 Uniform circular motion and SHM
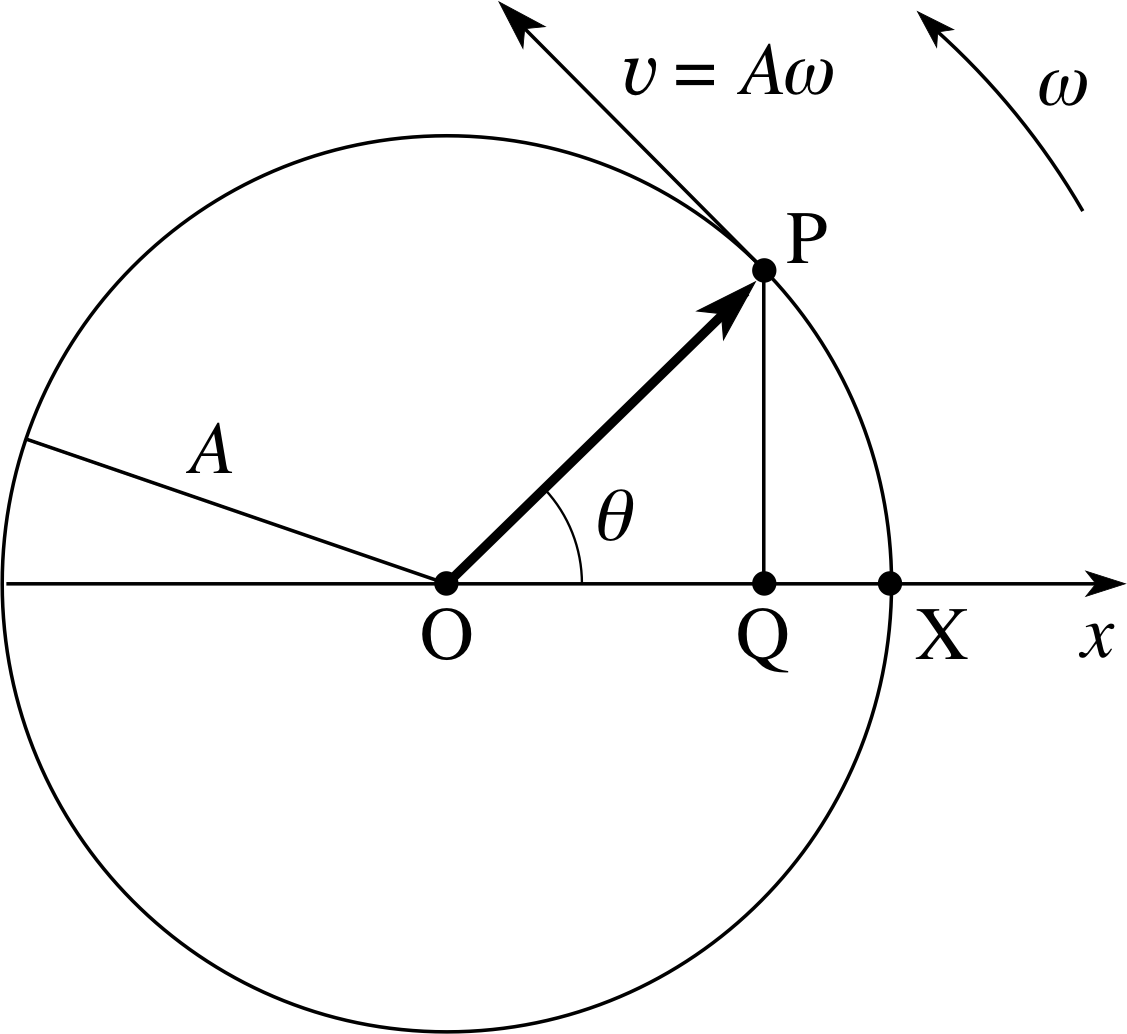
Figure 3 An object in uniform circular motion with an orbit radius shown in the figure.) The object is moving with constant angular speed ω, A, an angular speed ω and an orbital speed υ = Aω.
The Greek letter ω that is used to represent the angular frequency of an oscillator is also widely used to represent the angular speed of an object moving in a circle. This is no mere coincidence, rather it points to a deep association between one–dimensional simple harmonic motion and uniform circular motion. (An example of uniform circular motion would be the movement of a point on the rim of a uniformly rotating wheel of radius r. The direction of motion of such a point is changing all the time but its speed υ is constant, and so is its angular speed ω = υ/r.) This link between SHM and uniform circular motion provides valuable insight into the ideas of phase and angular frequency, as you are about to see.
Figure 3 shows an object in uniform circular motion about the origin of a Cartesian coordinate system. (The x–axis of the coordinate system is also at a fixed distance A from O, so its speed at any instant is given by υ = Aω.
✦ Imagine that you are located in the plane of Figure 3, looking at the circular path of the moving object ‘edge-on’, from a point outside the circle. Describe the apparent motion of the object from your viewpoint.
✧ The object would appear to move back and forth, periodically, along a straight line. The object’s displacement from the centre of its motion would vary smoothly from +A to −A and the apparent speed would also appear to change smoothly, attaining a maximum of Aω when the object passed through the centre of its apparent motion and diminishing to zero at the turning points. The period of this apparent linear motion would be equal to the time it took the moving object to complete one full circle, i.e. T = 2π/ω. (The object would appear to get bigger and smaller as it oscillated back and forth, but that is of no interest to us.)
In fact, the apparent linear motion seen from the plane of Figure 3 would be SHM with amplitude A (i.e. equal to the radius of the circle) and angular frequency ω (i.e. equal to the angular speed of the circular motion). Thus by viewing uniform circular motion in the right way we can obtain the ‘appearance’ of one–dimensional SHM. Or, to put it another way, with any given one–dimensional SHM of amplitude A and angular frequency ω we can associate a ‘fictional’ uniform circular motion of radius A and angular speed ω.
Now, how does this association between one–dimensional SHM and uniform circular motion help us to understand the phase that appears in mathematical representations of SHM such as Equations 5a and 5b?
x = A cos ωt(Eqn 5a)
x = A sin ωt(Eqn 5b)
Well, suppose that we start timing the motion in Figure 3 from the moment when the moving object crosses the x–axis at the point X. If the time taken for the object to reach the point P is t then we can say that θ = ωt, where θ is the angle between the line OP and the x–axis.
If we now imagine viewing this motion from the plane of Figure 3 and in a direction perpendicular to the x–axis, so that what we see appears to be one–dimensional SHM along the x–axis, then it is quite clear that the displacement of the moving object from the centre of the motion will be given by x = OQ = A cos θ = A cos ωt, i.e. Equation 5a.
Thus, given any example of SHM that can be described by Equation 5a, we can identify the phase ωt at any time t with the change in angular position θ of the moving object in the associated uniform circular motion. Furthermore, we can say that initially (when t = 0) the oscillator is at x = A and θ = 0.
Now suppose we observe the same circular motion again, but this time we start timing from the earlier moment when the moving object is directly below the origin in Figure 3. This means that by the time the moving object reaches the point X it will already have moved through an angle of π/2 radians (i.e. 90°). Under these conditions the angular position of the moving object after a time t will be θ = ωt − π/2 rad where θ is still being measured anticlockwise from the x–axis.
Viewing the motion from the plane of Figure 3 as before, but using the new starting time, the associated SHM must be represented by x = A cos θ = A cos(ωt − π/2). Thanks to a well known trigonometric identity which tells us that cos(ωt − π/2) = sin ωt we can represent the SHM by an equation of the form x = A sin ωt, i.e. Equation 5b. Thus, given any example of SHM that can be described by Equation 5b, we can again identify the phase ωt at any time as the change in angular position (θ) of the moving object in the associated uniform circular motion. However, in this case the oscillator is initially (at t = 0) at x = 0 and the initial value of θ is −π/2.
Note that in both the mathematical representations of SHM we have considered (Equations 5a and 5b) the interpretation of phase is the same – it’s the change in angular position of the moving object in the associated uniform circular motion. The only difference between the motions described by Equations 5a and 5b is the initial position of the oscillator and, correspondingly, the initial angular position of the moving object in the associated uniform circular motion.
Armed with this relationship between SHM and uniform circular motion we are now ready to examine the general mathematical definition of one–dimensional SHM. This deals with the case where the initial displacement of the oscillator may have any value between A and −A.
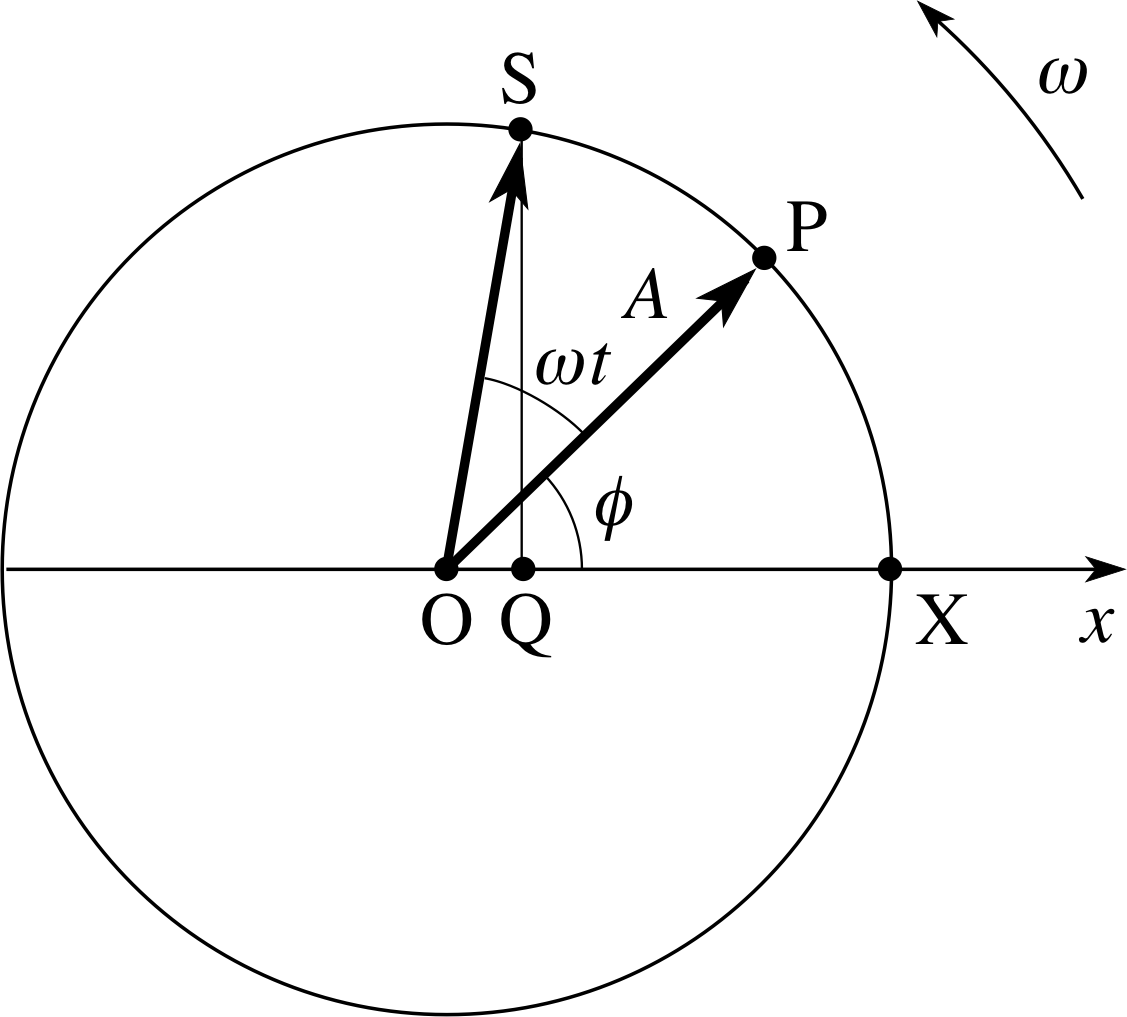
Figure 4 The uniform circular motion associated with one–dimensional SHM in the general case where the object has an initial angular position ϕ.
Question T3
Figure 4 illustrates general initial conditions for one–dimensional SHM, as represented by its associated circular motion. The initial time (t = 0) is when the object is at P, with an initial angular position ϕ. At a time t it is at S, having turned through an additional angle ωt. Use Figure 4 and basic trigonometry to derive an expression for the displacement x at time t in terms of A, ωt and ϕ.
Answer T3
At time t the angular position of the point S is θ = ωt + ϕ. Thus, x = A cos θ = A cos(ωt + ϕ).
We can now define one–dimensional SHM in terms of either of the following expressions for the displacement at time t.
$x(t) = A\cos\left(\dfrac{2\pi t}{T}+\phi\right) = A\cos(\omega t+\phi)$(6a)
or$x(t) = A\sin\left(\dfrac{2\pi t}{T+\phi}\right) = A\sin(\omega t+\phi$(6b) i
In these equations the quantity (ωt + ϕ) is the phase at time t and ϕ is the initial value of the phase at t = 0. Sometimes ϕ is called the phase constant of the motion. It is immaterial which of these two equivalent equations is used to represent a particular SHM since either is valid, with an appropriate choice of the phase constant.
Question T4
Choose appropriate values of the phase constant ϕ so that (a) Equation 6a becomes Equation 5b, and (b) Equation 6b becomes Equation 5a.
x = A cos ωt(Eqn 5a)
x = A sin ωt(Eqn 5b)
Answer T4
(a) To change Equation 6a,
$x(t) = A\cos\left(\dfrac{2\pi t}{T}+\phi\right) = A\cos(\omega t+\phi)$(Eqn 6a)
into Equation 5b,
x = A sin ωt(Eqn 5b)
we need to choose ϕ so that
A cos(ωt + ϕ) = A sin ωt
If we put ϕ = −π/2 we have
$A\cos\left(\omega t-\dfrac \pi2\right) = A\cos\left(\dfrac \pi2 - \omega t\right) = A\sin\omega t$
(b) To change Equation 6b,
$x(t) = A\sin\left(\dfrac{2\pi t}{T+\phi}\right) = A\sin(\omega t+\phi$(Eqn 6b)
into Equation 5a,
x = A cos ωt(Eqn 5a)
we need to choose ϕ so that
A sin(ωt + ϕ) = A cos ωt
If we put ϕ = π/2 we have
$A\sin\left(\omega t+\dfrac \pi2\right) = A\cos\left(\dfrac \pi2 - \omega t\right) = A\cos\omega t$
Study comment For the remainder of this module we will arbitrarily choose Equation 6a as our general definition of one–dimensional SHM.
Question T5
Sketch the graphs of Equation 6a,
$x(t) = A\cos\left(\dfrac{2\pi t}{T}+\phi\right) = A\cos(\omega t+\phi)$(6a)
over the time interval from t = 0 to t = 4π/ω (or to t = 2T) for the situations where (a) ϕ = 0, (b) ϕ = π/2, (c) ϕ = −π/2 and (d) ϕ = π.

Figure 21 See Answer T5.
Answer T5
The displacement–time graphs are shown in Figure 21, corresponding to Equation 6a, with phase constants ϕ of (a) 0, (b) π/2, (c) −π/2 and (d) π.
2.4 Velocity and acceleration in SHM
In Subsection 2.2 we noted that the gradient of the displacement–time graph at any time gives the velocity of the moving object at that time; the velocity–time graph of the moving object can thus be constructed from the displacement–time graph by measuring the gradient dx/dt of the latter graph at each point and by plotting this gradient as a function of time. The acceleration–time graph can then be constructed from the gradient dυx /dt of the velocity–time graph in a similar way. This graphical procedure is both slow and inaccurate.
Fortunately there is a quick and accurate alternative method for finding the gradient of a graph at any point, provided we know the algebraic expression that describes the curve, i.e. provided we know the function concerned. This method uses the techniques of differentiationdifferential calculus i to find the gradient of the graph. If the displacement x at time t is given by the function x (t) then the gradient of the displacement–time graph at time t is given by dx (t)/dt and this is also the instantaneous velocity υx(t) of the object at that time. In a similar way the gradient of the velocity–time graph at time t is given by dυx(t)/dt and this is also the instantaneous acceleration ax(t) of the object at time t. We can summarize these statements as follows:
$\upsilon_x(t) = \dfrac{dx(t)}{dt}$(7)
$a_x(t) = \dfrac{d\upsilon_x(t)}{dt} = \dfrac{d^2x}{dt^2}(t)$(8)
Note The symbol d2x/dt2(t) is called the second derivative of x with respect to t. It is an example of a higher derivative. See the Glossary for details.
So, starting from our chosen description of SHM, if we now substitute Equation 6a,
x (t) = A cos(ωt + ϕ)(Eqn 6a)
into Equations 7 and 8, and proceeding either graphically or via calculus, we find:
υx(t) = −Aωsin(ωt + ϕ)(9a)
andax(t) = −Aω2 cos(ωt + ϕ)(10a)
Comparison of Equation 6a and Equation 10a reveals that we may write
ax(t) = −Aω2 cos(ωt + ϕ) = −ω2x (t)(11a)
Figure 5 gives a quantitative representation of these results for the case ϕ = 0. These graphs were anticipated qualitatively in Question T1. Notice from Figure 5 that:
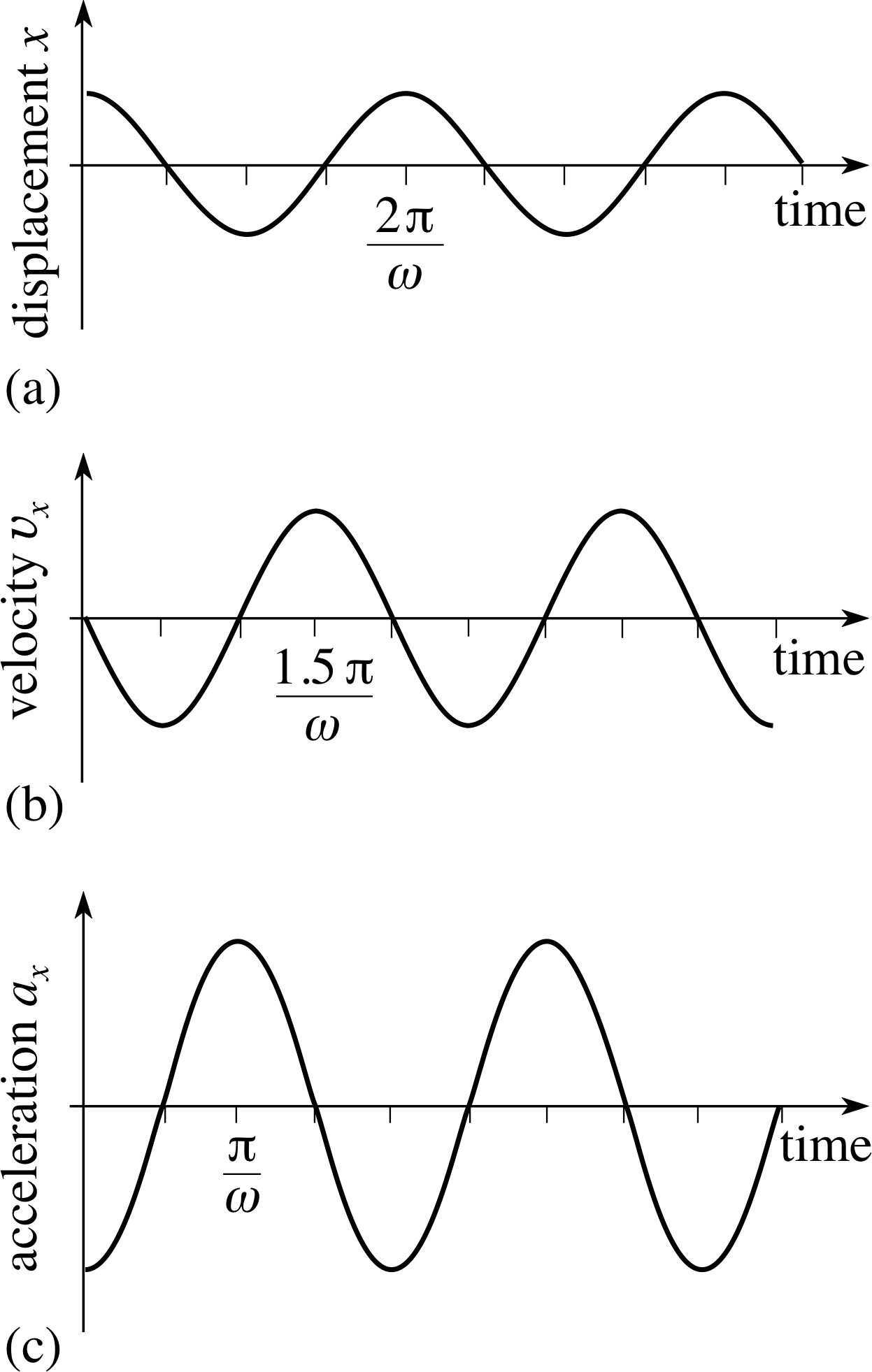
Figure 5 Graphs of the displacement, velocity and acceleration for an object in one–dimensional SHM, as represented by Equations 6a, 9a and 10a, with ϕ = 0.
- The velocity is maximum when the displacement is zero, and zero when the displacement is maximum – both graphs are sinusoidal but their respective maxima and minima are offset by a fixed time (0.5π/ω), or one–quarter of a period. This is because one is described by a sine function and the other by a cosine function of the same angle (Equations 6a and 9a).
- The acceleration and the displacement reach their turning points at the same time but one is a maximum when the other is a minimum. This is because both are described by cosine functions, but they have opposite signs (Equations 6a and 10a).
- The peak value of displacement is the amplitude of the motion A, while the peak value of velocity is ωA and that of acceleration is ω2A. This implies that the peak values of velocity and acceleration can be increased by increasing ω, even when the amplitude A is constant. This is what we might have expected, since increasing the frequency (f = ω/2π) at constant amplitude requires the object to cover the same path in a shorter time and therefore it must reach larger velocities and larger accelerations.
- If we compare the three graphs on Figure 5 we notice that each reaches its maximum positive value at different times – acceleration first at t = π/ω, then velocity at t = 1.5π/ω and finally displacement at t = 2π/ω. From this we say that the acceleration phase_leadleads the velocity by one–quarter of a cycle or by a phase of π/2. Similarly the velocity leads the displacement by π/2. Alternatively we might say that the displacement phase_laglags the velocity by π/2 and the velocity lags the acceleration by π/2. i When the phase difference is π (as with acceleration and displacement) it is equally valid to describe this as a lead or a lag by π.
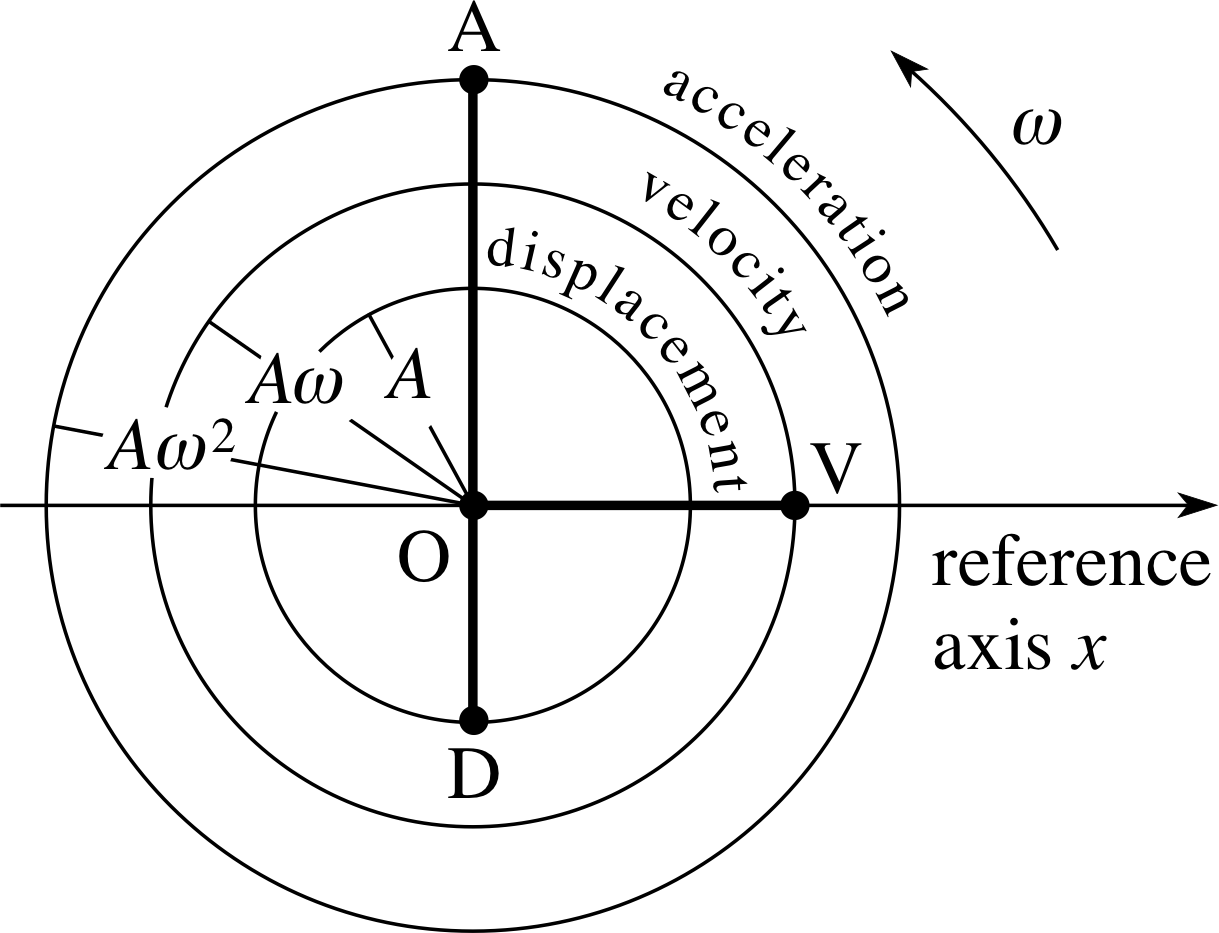
Figure 6 The rotating wheels analogue for displacement, velocity and acceleration in one–dimensional SHM.
When two quantities that vary sinusoidally i reach their maxima simultaneously we say they are in phase and when they have a phase difference of π (such as displacement and acceleration in our example) we say they are in anti–phase or alternatively 180° out of phase. These phase differences can again be visualized with the help of the circular motion SHM analogue. Figure 6 shows a schematic representation of the relative phases of displacement, velocity and acceleration in one–dimensional SHM. The figure shows three wheels, representing displacement, velocity and acceleration; each wheel has a radius corresponding to the maximum magnitude of the quantity concerned: xmax = A, (υx)max = Aω, (ax)max = Aω2. The three wheels are joined together by three rigid spokes OD, OV and OA, and rotate at a common angular speed ω around O. At any time the displacement x, velocity υx and acceleration ax are represented by the x–coordinates of points D, V and A, respectively. As the wheels rotate, the first spoke to cross the positive x–axis is the ‘acceleration spoke’ followed next by the ‘velocity spoke’ and finally the ‘displacement spoke’. Since these three spokes are mounted 90° or π/2 radians apart the phase differences are maintained at π/2 radians or one–quarter of a full cycle. This also brings out the fact that the phase differences are more significant than the phases (ωt + ϕ) themselves, since the former stay constant while the latter change with the rotation of the wheels.
Also, if the wheels were to rotate clockwise rather than anticlockwise then we would have to reverse the terms ‘lead’ and ‘lag’ but the magnitude of the phase differences would be unchanged. A similar conclusion would be reached from Figure 5, if we reversed the direction of the time axis.
Question T6
Describe in words the changes you would expect to see in Figure 5 if it had been plotted for the case ϕ = π/3 instead of ϕ = 0.
Answer T6
The effect would be the same as that achieved by moving the vertical axis of each graph to the point currently at t = π/(3ω), and by relabelling the axis so that this point becomes the new zero for time.
In our derivation of Equations 9a, 10a and 11a
υx(t) = −Aωsin(ωt + ϕ)(Eqn 9a)
ax(t) = −Aω2 cos(ωt + ϕ)(Eqn 10a)
ax(t) = −Aω2 cos(ωt + ϕ) = −ω2x (t)(Eqn 11a)
we have arbitrarily chosen to express the displacement by the cosine function, Equation 6a,
x (t) = A cos(ωt + ϕ)(Eqn 6a)
We could equally well have chosen to represent the displacement by the sine function, Equation 6b,
x (t) = A sin(ωt + ϕ)(Eqn 6b)
Had we used the sine function representation we would have produced the following equivalent expressions:
υx(t) = −Aω cos(ωt + ϕ)(9b)
andax(t) = −Aω2 sin(ωt + ϕ)(10b)
soax(t) = −Aω2 sin(ωt + ϕ) = −ω2x (t)(11b)
When we compare Equations 11a and 11b we notice that the same result is produced when the acceleration is expressed in terms of the displacement.
ax(t) = −ω2x (t)(12)
It is clear that the result expressed by Equation 12 is a fundamental statement concerning SHM, since it is independent of the choice of how the displacement is represented. Since ω and ω2 are constants, Equation 12 reveals a very important feature that could be regarded as a definition of SHM:
In one–dimensional SHM, the acceleration at any instant is linearly proportional i to the displacement at that instant and is always in the opposite direction to the displacement.
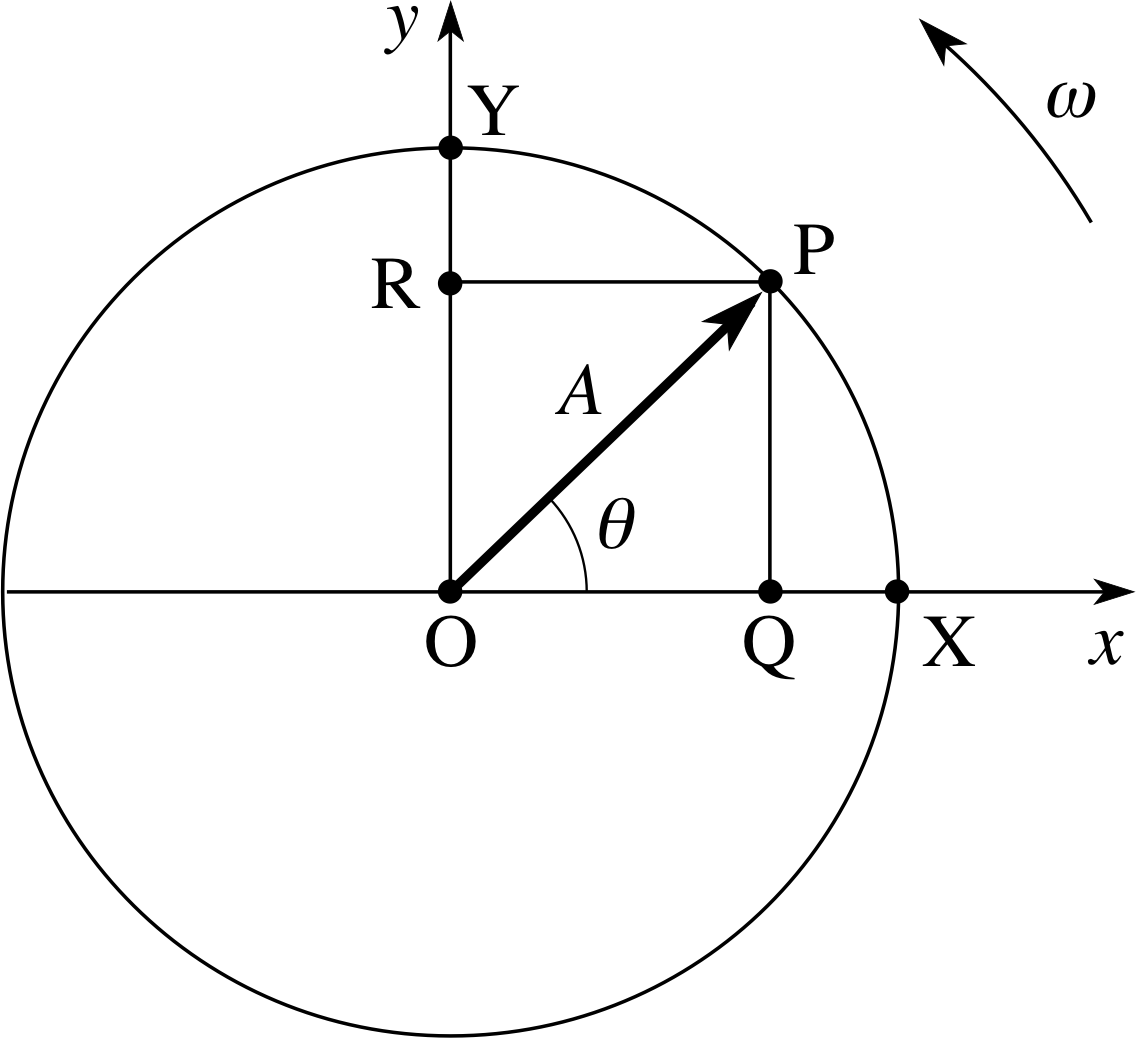
Figure 7 The phasor model for one–dimensional SHM.

Figure 3 An object in uniform circular motion with an orbit radius A, an angular speed ω and an orbital speed υ = Aω.
2.5 The phasor model of SHM
We have seen that a uniform circular motion can be associated with one–dimensional SHM. In this association a diameter of the circle is taken as the x–axis, and the SHM appears as the x–component of the motion around the circle. Sometimes the SHM is described as the projection of the circular motion along the diameter. The reason why this is useful is that it gives a clear visual representation of the three characteristics which define any SHM – the amplitude, the frequency and the phase. The amplitude corresponds to the radius of the circle, the frequency to the number of rotations of the object around the circle in unit time and the phase to the angle θ between the x–axis and the line joining the centre of the circle to the position of the rotating object at the time concerned. In fact, this simple geometrical construction is even more useful than we have shown so far. For example, as we shall see in Section 3, it allows us to see what happens when an object moves under the influence of several SHMs simultaneously. However, in order to do this we need to introduce a new method of representing or modelling SHM mathematically.
This new representation is called the phasor model and is illustrated in Figure 7.
Figure 7 has much in common with Figure 3 though a y–axis has been added for later convenience. Nonetheless, the main difference is one of terminology in that the displacement vector $\overrightarrow{OP}$ of the circular motion will henceforth be referred to as the displacement phasor of the simple harmonic motion. The length of the phasor, A, is called its amplitude while the angle θ between the phasor and the x–axis is called its phase. In principle we can now describe a given SHM in terms of its associated (rotating) displacement phasor – we need not think about circular motion at all. Phasor diagrams similar to Figure 7 can be drawn to represent the displacement, velocity, or acceleration of the oscillating object at any given time – that is to give the amplitude and phase of the displacement, velocity, or acceleration at that time.
Question T7
Draw a phasor diagram showing the velocity phasor for the object when it is at point P in Figure 7. What is the angle between the velocity phasor and the horizontal axis? Is this consistent with our earlier remarks about the phase difference between velocity and displacement? Take care to indicate the amplitude of the velocity phasor and to label the horizontal and vertical axis of your diagram correctly.
Answer T7
From Figure 7, at P the displacement phasor $\overrightarrow{OP}$ makes an angle θ with the positive x–axis. From Figure 3 we see that the velocity phasor at P must be tangential to the circle and is rotated through +π/2 (anti-clockwise) from $\overrightarrow{OP}$. Therefore, the angle between the velocity phasor and the horizontal axis is θ + (π/2).
This is shown in Figure 22 and is consistent with our earlier claim, in Subsection 2.4, that the velocity leads the displacement by π/2.
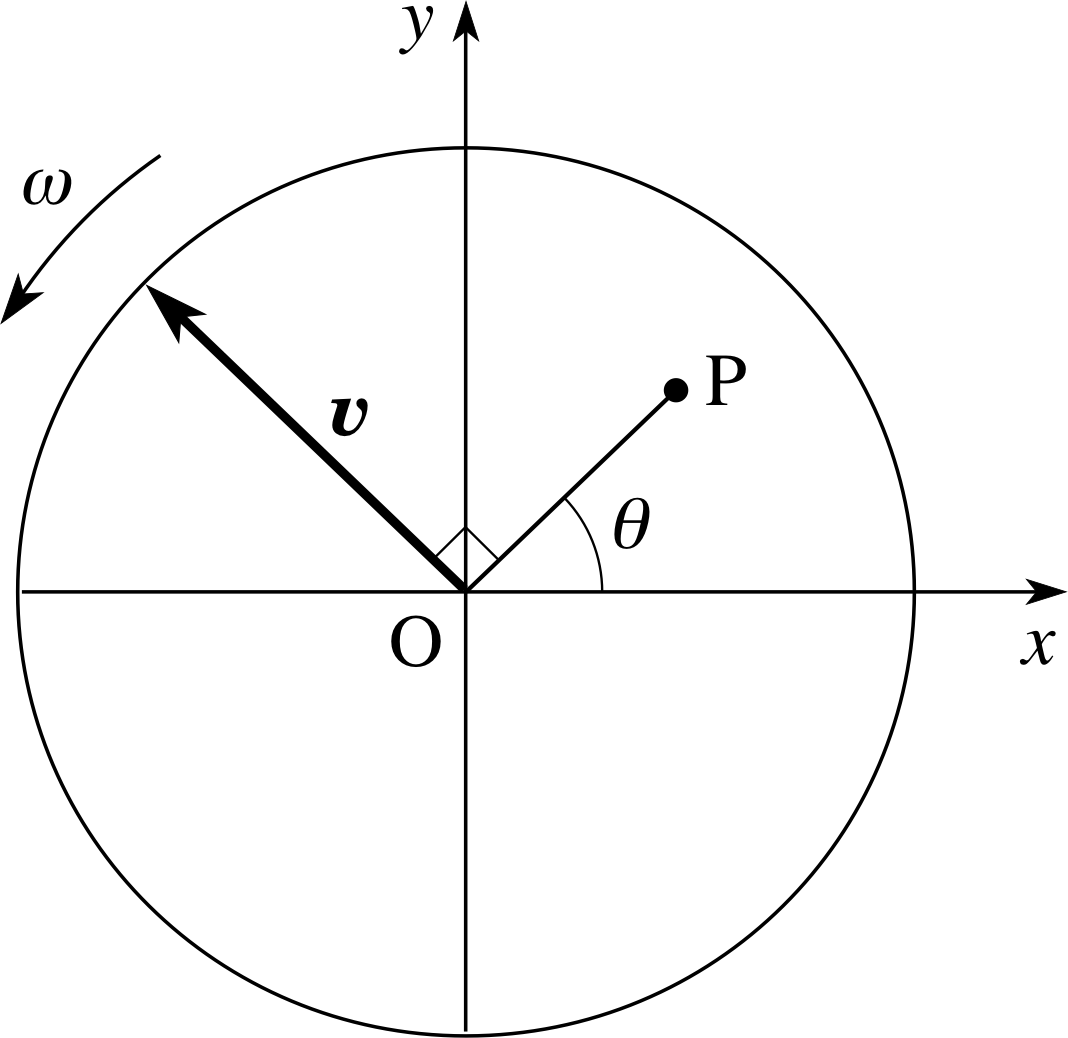
Figure 22 See Answer T7.

Figure 7 The phasor model for one–dimensional SHM.

Figure 3 An object in uniform circular motion with an orbit radius A, an angular speed ω and an orbital speed υ = Aω.
Question T8
Referring to Figure 7, show that the point R also executes SHM, where OR is the component of $\overrightarrow{OP}$ along the y–axis. What is the phase difference between the displacements y and x of points R and Q?

Figure 7 The phasor model for one–dimensional SHM.
Answer T8
From Figure 7, y (t) = OR = A sin θ = A sin(ωt + ϕ) when we replace the phasor angle θ by our general SHM phase (ωt + ϕ). From Answer T4(b) we know that if we choose ϕ = π/2 this equation becomes A cos ωt. This means that if we advance the phase of the y–motion it then matches the phase of the x–motion; this implies that, initially, the y–motion lags the x–motion by π/2. This is clear directly from Figure 7, since P reaches point X before point Y and when Q is at X, R is at O and will not reach Y until later.
There is a clear similarity between phasors and vectors. Each is represented diagramatically as a directed line segment, though a vector represents magnitude and direction, whereas a phasor represents amplitude and phase. Just as we are able to combine several vectors to find a resultant vector, using the rules of vector addition, so too we can combine several phasors, each representing one SHM, to find a resulting phasor which will indicate the result of the addition or superposition of several SHMs. We will return to this important idea in Section 3.
2.6 Forces acting in SHM
We now turn our attention to the forces acting in SHM. We will see that this approach leads us to another alternative specification of SHM – whereby if a body is subject to a particular force then it must necessarily undergo SHM.
The force acting on an object is related to the acceleration of the object through Newton’s second law of motion, F = ma. Equation 12 gives the acceleration at time t in terms of the displacement at time t. We can use this result to infer the force acting in SHM. If the object has mass m then the x–component of the force acting at time t must be given by the expression:
Fx(t) = max(t) = −mω2x (t)(13)
The significance of Equation 13 is the following:
In SHM the magnitude of the force acting at any time is linearly proportional to the distance from equilibrium at that time and the direction of the force is opposite to that of the displacement, i.e. towards the equilibrium position.
Thus the force causing SHM always acts in a direction that tends to reduce the displacement and for this reason it is usually called the restoring force.
Equation 13 gives us a general expression for the restoring force acting on any SHM oscillator, in terms of the mass and the angular frequency of oscillation. It implies that the force responsible for SHM is linearly proportional to the displacement x from the position of equilibrium and is always directed towards it. We could put this in a more enlightening way by saying:
SHM will occur whenever an object moves from equilibrium under a restoring force which is linearly proportional to the displacement from equilibrium – that is it moves under the influence of a linear restoring force.
The constant of proportionality in Equation 13, k = mω2, is called the force constant for the motion. i
For any SHM this force constant relates the restoring force to the displacement and is itself related to the frequency of oscillation
$k = -\dfrac{F_x(t)}{x(t)} = m\omega^2$(14)
so$\omega = \sqrt{\dfrac km}$(15)
and the period of the oscillation is given by Equation 4,
$T = \dfrac1f = \dfrac{2\pi}{\omega}$(Eqn 4)
as
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac mk}$(16)
✦ What are the SI units of the force constant?
✧ From Equation 14,
$k = -\dfrac{F_x(t)}{x(t)} = m\omega^2$(Eqn 14)
x (t) k = −Fx1/x and so the units are N m−1.
Notice a new striking feature of SHM, as seen from Equation 16:
The period does not depend on the amplitude of the motion but only on the mass of the object and on the force constant. This is so in SHM because the restoring force varies linearly with the displacement.
2.7 Examples of SHM
In this section we consider some simple examples of SHM and confirm that the motions are indeed governed by restoring forces of the type given by Equation 13, provided the oscillations are of sufficiently small amplitude.
An object attached to a spring and displaced horizontally
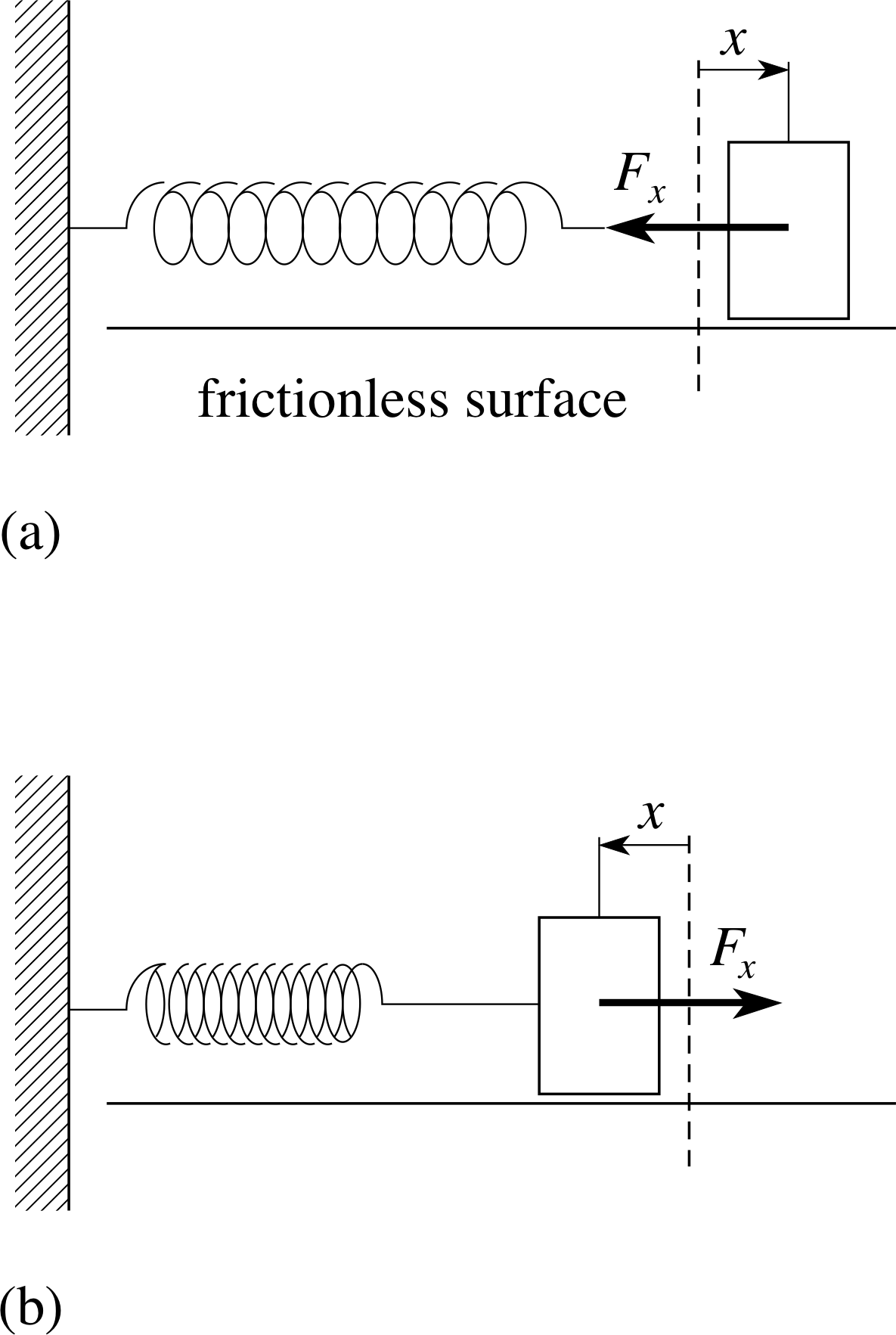
Figure 8 The horizontal oscillations of a mass attached to a fixed spring and moving on a horizontal frictionless surface. (a) Positive displacement, negative force and (b) negative displacement, positive force.
Provided a spring is not overextended it will obey Hooke’s law. This law states that the force in the spring (i.e. the tension) is proportional to the extension. If the spring is stretched or compressed by an amount x then the x–component of the force in the spring is given by
Fx = −kx(17)
where the force constant k is called the spring constant. The negative sign indicates that the spring tries to regain its original unstretched length, so the tension acts in the opposite direction to the extension and thus is a restoring force.
If no other forces act then Hooke’s law provides a linear restoring force and thus satisfies the general condition for SHM. If we identify the spring’s extension from its original length with the displacement x in Equation 13,
Fx(t) = max(t) = −mω2x (t)(Eqn 13)
we can anticipate that there will be SHM oscillations of this extension about zero extension. To observe these oscillations we arrange that the Hooke’s law force is the only net force acting on the mass attached to the spring. We can do this by placing the spring and the mass on a horizontal frictionless surface and by considering the horizontal motion of the mass attached to the fixed spring. Gravity plays no part in this motion since it acts vertically and the weight of the mass is supported by the reaction from the surface. This is shown in Figure 8 for both positive and negative displacements.
The equation of motion of the mass m is given by Newton’s second law, F = ma, where Fx = −kx, is the restoring force in the spring. i Equations 14, 15 and 16
$k = -\dfrac{F_x(t)}{x(t)} = m\omega^2$(Eqn 14)
$\omega = \sqrt{\dfrac km}$(Eqn 15)
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac mk}$(Eqn 16)
are then directly applicable, but with k interpreted as the spring constant.
An object attached to a spring and displaced vertically
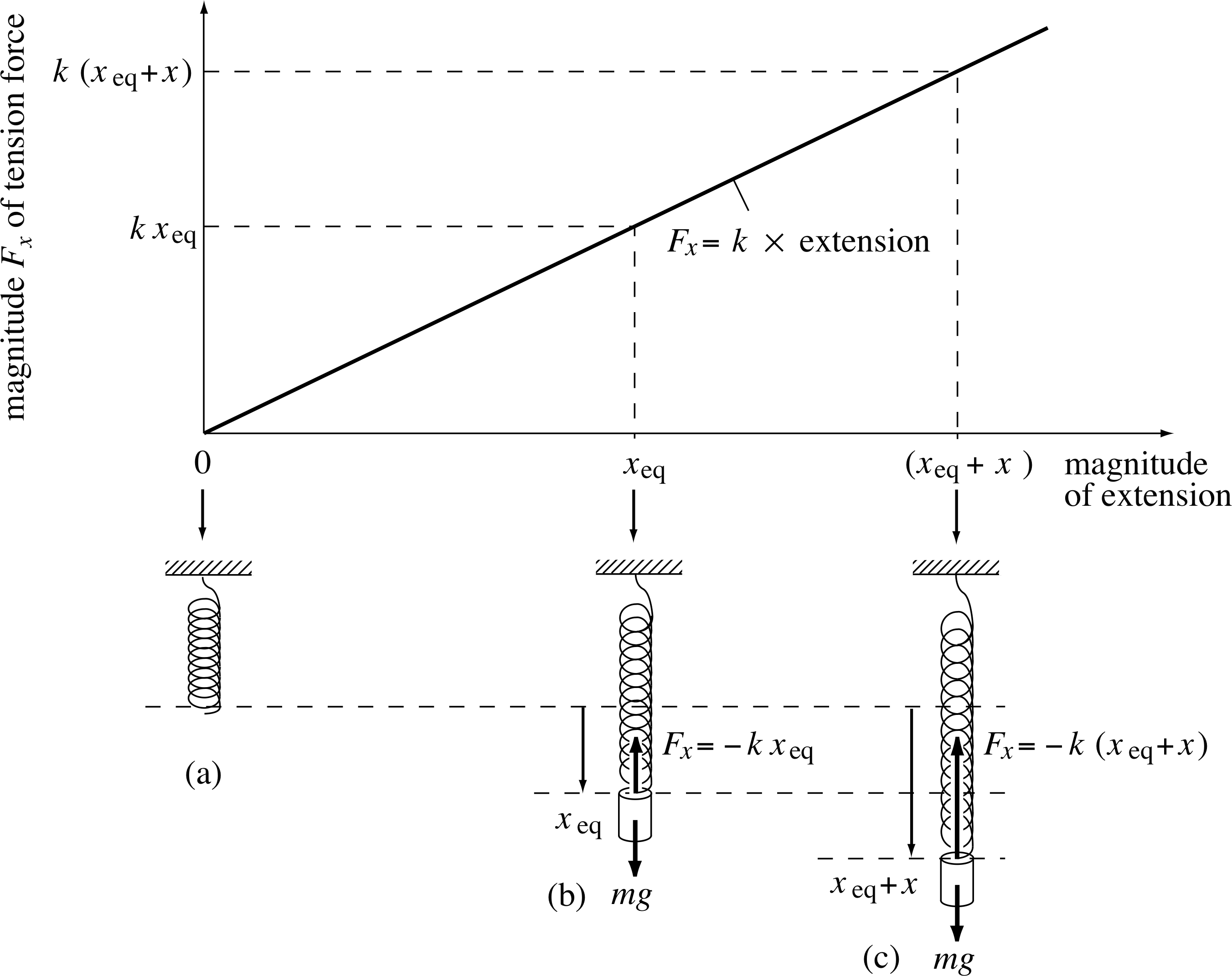
Figure 9 A light coil spring shown (a) unloaded, (b) at equilibrium under load, (a) and (c) loaded as before but displaced below its position of equilibrium.
This is the situation depicted in Figure 9. The position of equilibrium of the mass is with the spring already extended under the weight of the mass. Let xeq be its extension at equilibrium (measured downwards as positive).
Vertical equilibrium implies that the net force on the mass is zero or that the weight of the mass mg downwards is balanced by the spring tension upwards, due to the extension xeq (Figure 9b).
This condition is
mg − kxeq = 0(18)
If the suspended body is given a further displacement x from the position of equilibrium the total extension is (xeq + x) as illustrated in Figure 9c. i The net force downwards Fx is
Fx = mg − k (xeq + x)
Substituting for mg from Equation 18 we find
Fx = −kx
which again gives SHM about the position of equilibrium.
Thus we see that if a mass is attached to a spring and is allowed to oscillate, either with horizontal or with vertical motion, then SHM occurs – providing the extension from equilibrium is sufficiently small that Hooke’s law holds true. The value of ω for the oscillations is given by Equation 15,
$\omega = \sqrt{\dfrac km}$(Eqn 15)
Equations 14, 15 and 16 are all directly applicable, with k interpreted as the spring constant.
Oscillations of a simple pendulum
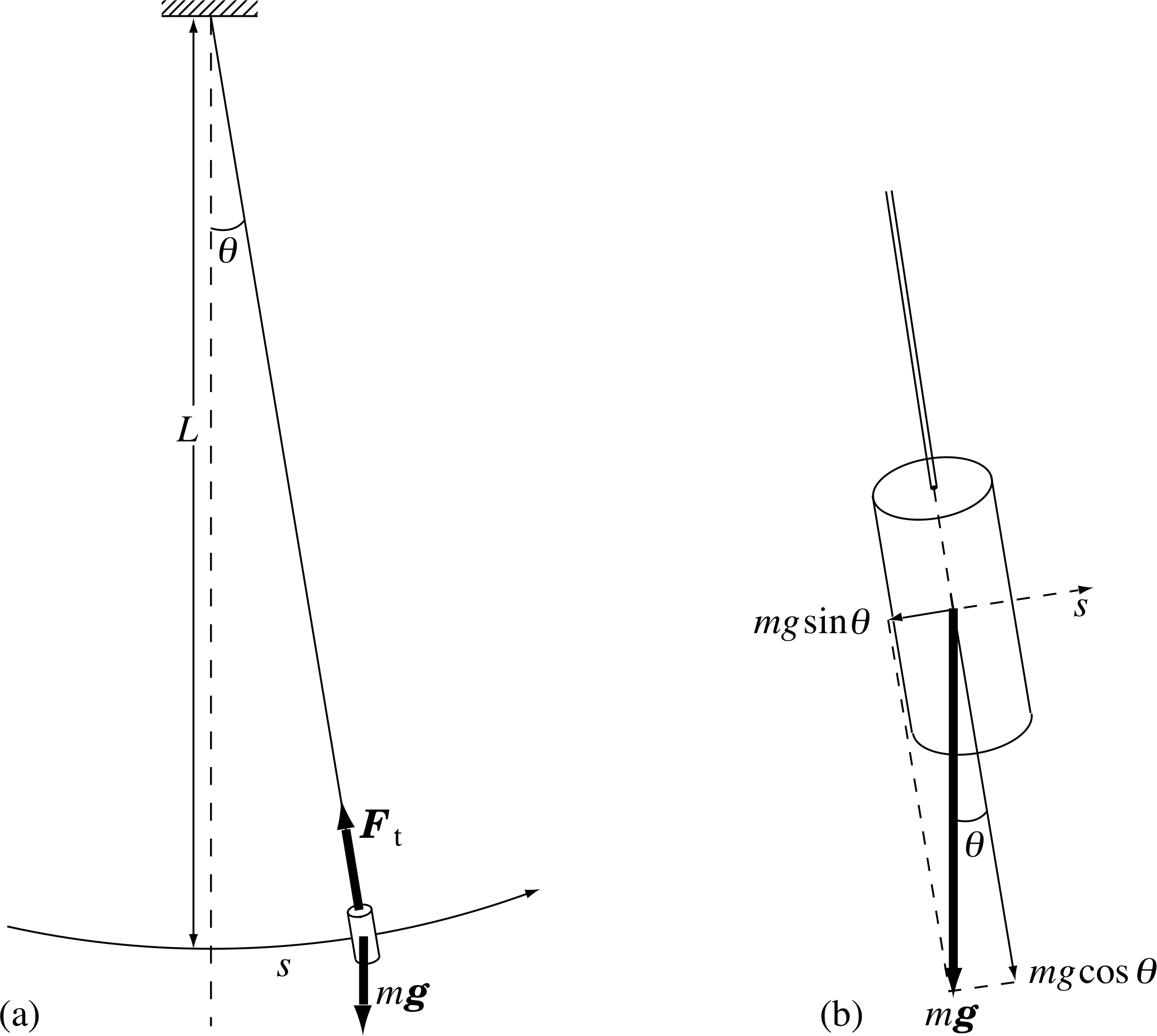
Figure 10 (a) A simple pendulum in motion. (b) The restoring force is provided by the component of the weight of the bob along the tangent to the arc,
A simple pendulum is one for which the mass of the supporting thread is negligible compared to the mass of the pendulum bob and the bob has negligible size compared to the length of the pendulum. When a simple pendulum of length L swings in a vertical plane the bob moves along the arc of a circle, as shown in Figure 10a, and when the pendulum is at an angle θ to the vertical its displacement along the arc from the position of equilibrium is s = Lθ. i
The position of equilibrium is where the bob hangs vertically, with its weight supported by the tension in the thread. When the bob is displaced to one side, the tension in the thread Ft acts at right angles to the tangent to the arc, and therefore has no component along this tangent, so it does not influence the motion along the tangent to the arc. The only force along the tangent arises from the component of the weight resolved in this direction; since this force always acts towards the position of equilibrium, it is a restoring force.
If we can show that this component is proportional to the displacement from equilibrium then we can be confident that SHM will occur. The weight and the restoring force are shown in Figure 10b, from which it can be seen that the component of this force along the tangent, Fs, is given by
Fs = −mg sin θ
where the positive direction of s is defined in Figure 10b and positive θ is taken to be to the right of the vertical.
We can use the fact that s = Lθ to write this as
$F_s = -mg\sin\theta\left(\dfrac{s}{L\theta}\right) = -\dfrac{mg}{L}\left(\dfrac{\sin\theta}{\theta}\right)$(19)
For SHM this would have to have the form Fs = −ks. Since the factor (sin θ/θ) is not constant as θ varies, the motion is not SHM. However, if we limit the oscillations to small values of θ then we can use the approximation that sin θ ≈ θ (provided θ is in radians) and Equation 19 then approximately takes the form expected for SHM:
$F_s = -\left(\dfrac{mg}{L}\right)$(20)
If we compare Equation 20 with the general result for SHM (Equation 13)
Fx(t) = max(t) = −mω2x (t)(Eqn 13)
we find$-m\omega^2 = -\dfrac{mg}{L}$
or$\omega = \sqrt{\dfrac gL}$(21)
and the period of the pendulum is given by Equation 4,
as$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac Lg}$(22)
Notice that for small displacements from equilibrium the period of a simple pendulum is independent of the mass of the bob and depends only on the length of the pendulum and the magnitude of the acceleration due to gravity g. This fact is often used to measure g, from the observed period of a simple pendulum.
Question T9
(a) A body of mass 2.0 kg is suspended from the end of a spring whose spring constant is k = 4.0 × 102 N m−1. What is the period for small oscillations? (b) Calculate the period for small oscillations of the same mass, when used as the bob of a simple pendulum of length 12 m. (g = 9.8 m s−2)
Answer T9
(a) The period of the oscillation can be calculated from Equation 16,
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac mk}$(Eqn 16)
$T = \rm 2\pi\sqrt{\dfrac{2.0\,kg}{4.0\times10^2\,N\,m^{-1}}} = 2\pi\sqrt{\dfrac{5.0\times10^{-3}\,kg}{kg\,m\,s^{-2}\,m^{-1}}} = 0.44\,s$
(b) Equation 22,
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac Lg}$(Eqn 22)
tells us that the mass of the bob is irrelevant here, only g and the length of the pendulum are involved. We find
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac Lg} = \rm 2\pi \sqrt{\dfrac{12\,m}{9.8\,m\,s^{-2}}}$
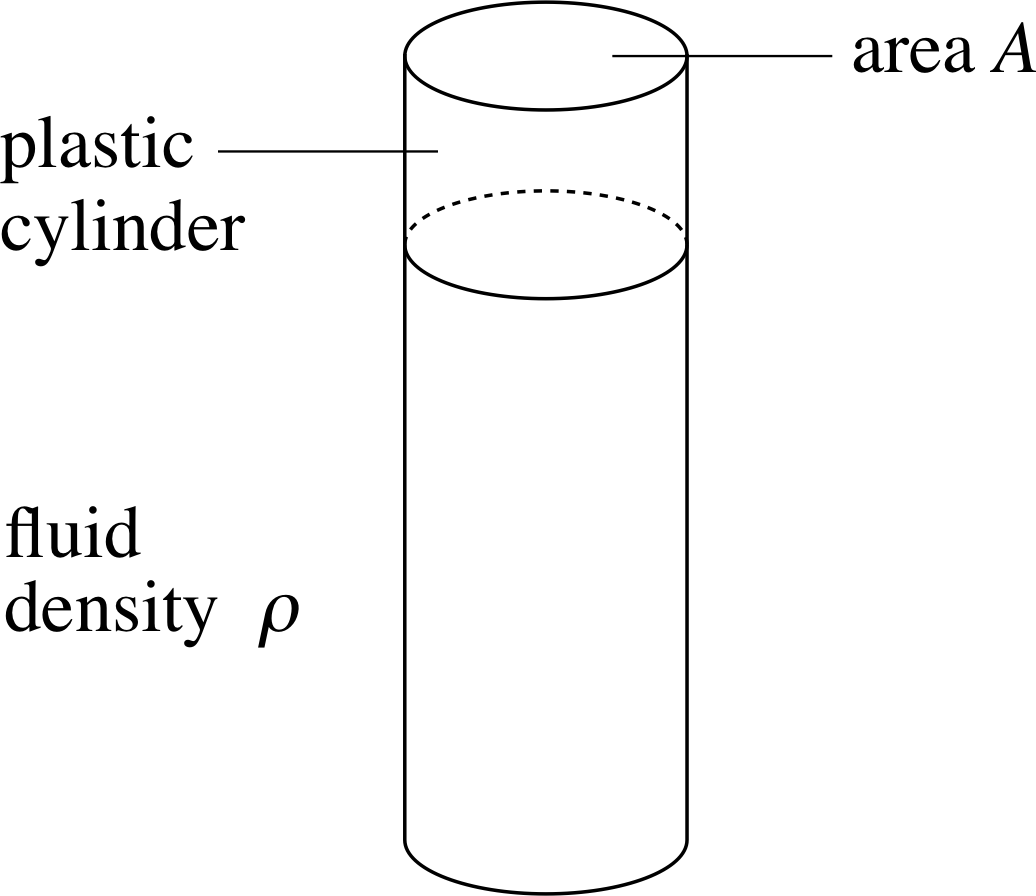
Figure 11 See Question T10.
Question T10
A cylinder of mass M and cross–sectional area A floats upright in a fluid of density ρ (see Figure 11). Ignoring all forces other than buoyancy, i show that, if disturbed, the cylinder will execute SHM vertically. Obtain an expression for the period of the motion.
Answer T10
The restoring force here is the buoyancy force. This is the weight of the fluid which would occupy the volume of the submerged part of the cylinder. In equilibrium, the cylinder will float so that the submerged volume is sufficient for the buoyancy force to support the weight of the cylinder. When it is pushed down a further distance x it will experience an additional restoring buoyancy force of Fx = Aρgx. We see that this force is proportional to the displacement x and we can confidently predict that SHM will follow. We compare the restoring force with the general SHM form from Equation 13,
Fx(t) = max(t) = −mω2x (t)(Eqn 13)
to find the angular frequency and hence the period:
Fx = −Aρgx = −Mω2x
The force constant is Aρg and the angular frequency of the SHM is therefore $\omega = \sqrt{\dfrac{A\rho g}{M}}$. The period is
$T = 2\pi\sqrt{\dfrac{M}{A\rho g}}$
Next we consider two real examples of SHM which seem rather remote from springs and pendula, but which nevertheless can be treated in terms of our mathematical model of SHM. The examples also show how widespread SHM is in nature and how SHM can be used to diagnose the forces acting in situations which are otherwise inaccessible to us.
Question T11
An electron in the Earth’s ionosphere i is found to be oscillating at a frequency of 800 kHz. If the mass of the electron is 9.1 × 10−31 kg, calculate the force constant involved in the oscillation.
Answer T11
Equation 13,
Fx(t) = max(t) = −mω2x (t)(Eqn 13)
relates the SHM force constant to the mass of the moving object:
Fx = −mω2x
The force constant is
mω2 = 9.1 × 10−31 kg × (2π × 8 × 105 s−1)2
mω2 = 2.3 × 10−17 kg s−2 = 2.3 × 10−17 kg m s−2 m−1
mω2 = 2.3 × 10−17 N m−1
This seems to be a very weak force constant in terms of a spring constant!
Question T12
In an oxygen nucleus the eight protons are able to oscillate collectively as one, in anti–phase with the eight neutrons, at a frequency of 5.3 × 1021 Hz. Estimate the force constant for the nuclear oscillation, given that this oscillation may be treated as equivalent to the SHM of a single particle (of mass equal to four proton masses) i about the centre of mass of the system. The proton mass is 1.67 × 10−27 kg.
Answer T12
We use the same approach as for Question T11. The relevant mass is now the mass of four protons, moving together.
The force constant is
mω2 = 4 × 1.67 × 10−27 kg × (2π × 5.3 × 1021 s−1)2 = 7.4 × 1018 N m−1
In this case the force constant is very much larger, and would certainly be impossible as a conventional spring!
2.8 The widespread occurrence of SHM; linear systems
SHM is the simplest kind of oscillation which can occur when a system is displaced from equilibrium. It arises whenever there is a restoring force which depends linearly on the displacement from equilibrium. It is easy to appreciate why this definition leads to a wide range of SHMs in nature since many equilibrium situations give rise to a linear restoring force, providing the displacement from equilibrium is sufficiently small.
We can understand this in terms of a general mathematical result. When any stable equilibrium situation is displaced there will be a restoring force which depends in some way on the displacement – that is, it is some function of displacement. If we imagine a graph of this function it can almost always be approximated by a linear function of displacement over a sufficiently small range. We have seen this already for the spring and the pendulum but it is equally true for sufficiently small disturbances of very many stable equilibrium situations. Systems which can be adequately described by this linear approximation are said to be linear systems.
It may be that the linear approximation is not appropriate for a particular situation because we must deal with displacements which are not sufficiently small. We have already seen examples of this for large amplitude oscillations of a mass on a spring or large swings of a pendulum. Such systems are said to be non–linear systems and oscillations which are significantly non–linear are called anharmonic oscillations. These are much more complicated to analyse than linear oscillations. In anharmonic oscillations we usually find that the period depends on the amplitude of the motion. We will not consider these further in this module.
3 Superposition of SHMs
In Section 2 we have examined the basic ideas of SHM. We now extend this to consider what happens in the common situation where the motion of an object results from the combination of several independent SHM oscillations at the same time. Sometimes these independent oscillations involve colinear displacements (i.e. along the same line) and sometimes they are in different directions. An example of the former would be the in and out vibrations of the cone of a loudspeaker, when driven by an amplifier. An example of the latter would be the motion of a ship in a rough sea – up and down, side to side, stern to prow.
Another example of the addition of displacements in different directions is the motion of an atom in a crystal. Each atom experiences a force from neighbouring atoms. These forces have attractive and repulsive aspects and so act rather like springs connecting the atoms together. We can model this by imagining each atom to be attached to three springs, one along each of the three coordinate axes x, y and z of the crystal. A particular atom will then oscillate about a position of equilibrium under the combined effect of three mutually perpendicular motions along each of these axes. This three–dimensional oscillation sounds dreadfully complicated but it is actually surprisingly easy to deal with in terms of the addition of three independent one–dimensional motions in x, y and z. From what you saw in Questions T11 and T12 you might correctly anticipate that if you were to measure the frequencies of these oscillations you would be able to infer the spring constants for the interatomic forces, and these may be different in the x, y and z directions.
The general term to describe the addition of two or more oscillations is superposition. The superposition principle simply states that:
When several oscillations are added, the resulting displacement at any time is the sum of the displacements due to each oscillation at that time.
The superposition principle is valid only for linear systems since it rests on the linear response of the system to the combined oscillation, and therefore all displacements must remain sufficiently small. Superposition of oscillations in linear systems is the subject of this section and it involves the application of some trigonometry. i
3.1 Superposition of colinear SHMs: beating and beat frequency
Consider the superposition of two SHM displacements along the x–axis
x (t) = x1(t) + x2(t)(23)
In general, the two SHMs may have different amplitudes, angular frequencies and phase constants so we can use Equation 6a,
$x(t) = A\cos\left(\dfrac{2\pi t}{T}+\phi\right) = A\cos(\omega t+\phi)$(Eqn 6a)
to write this as
x (t) = A1 cos(ω1t + ϕ1) + A2 cos(ω2t + ϕ2)(24)
The problem that now confronts us is that of gaining some insight into the nature of the combined displacement x (t). For example, what will the displacement–time graph look like? We will approach this general problem gradually, by assuming first that the frequencies and amplitudes are equal and that only the phase constants differ. We will then relax these conditions progressively so that we can return eventually to the general case of Equation 24. Initially we will use trigonometry but for the more complicated cases it is more sensible to use the phasor model.
Superposition of two equal amplitude and frequency SHMs
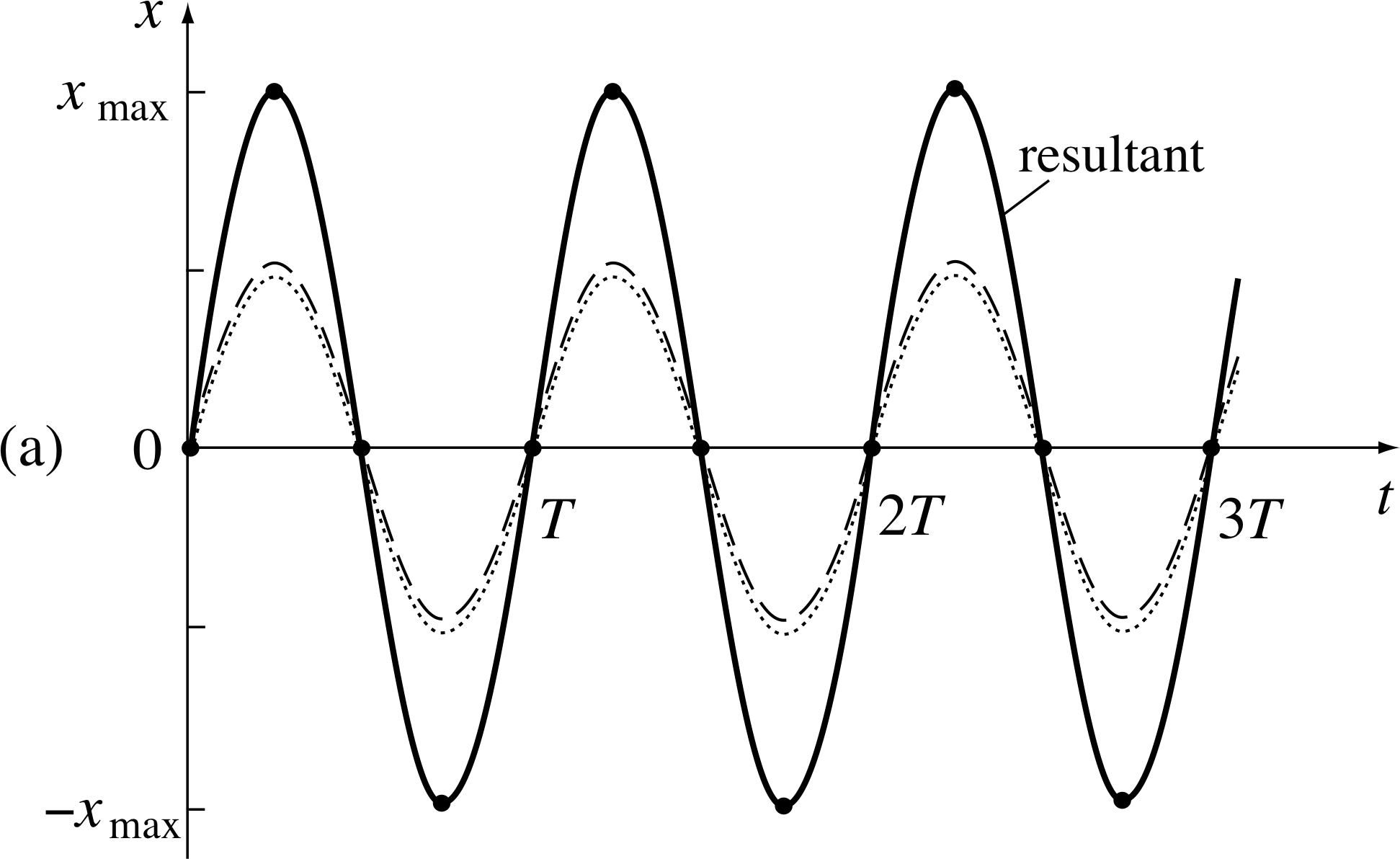
Figure 12a Superposition of two SHMs of the same amplitude and frequency and in phase
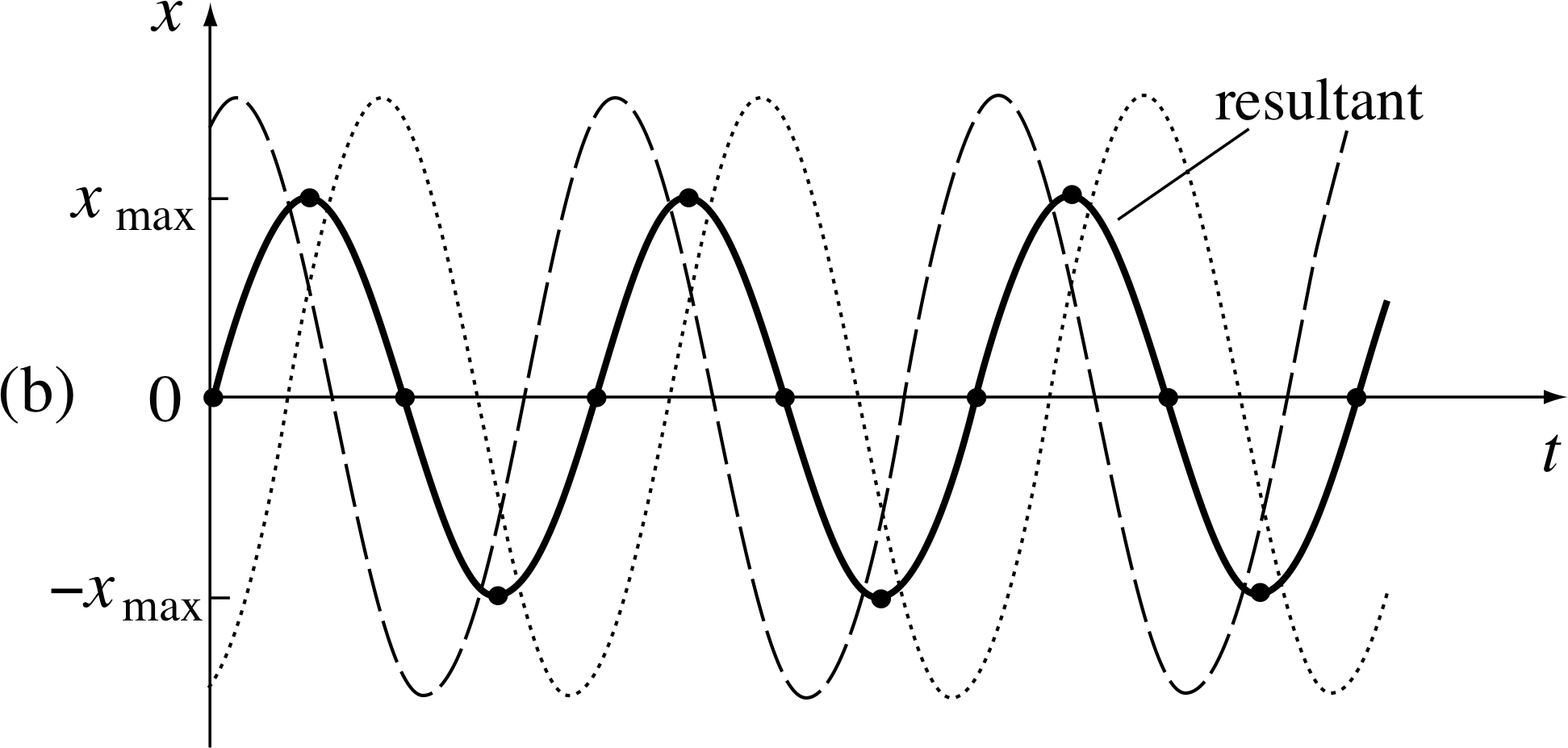
Figure 12b Superposition of two SHMs of the same amplitude and frequency, acting in the same direction, but differing in phase constant.and so having a general phase difference
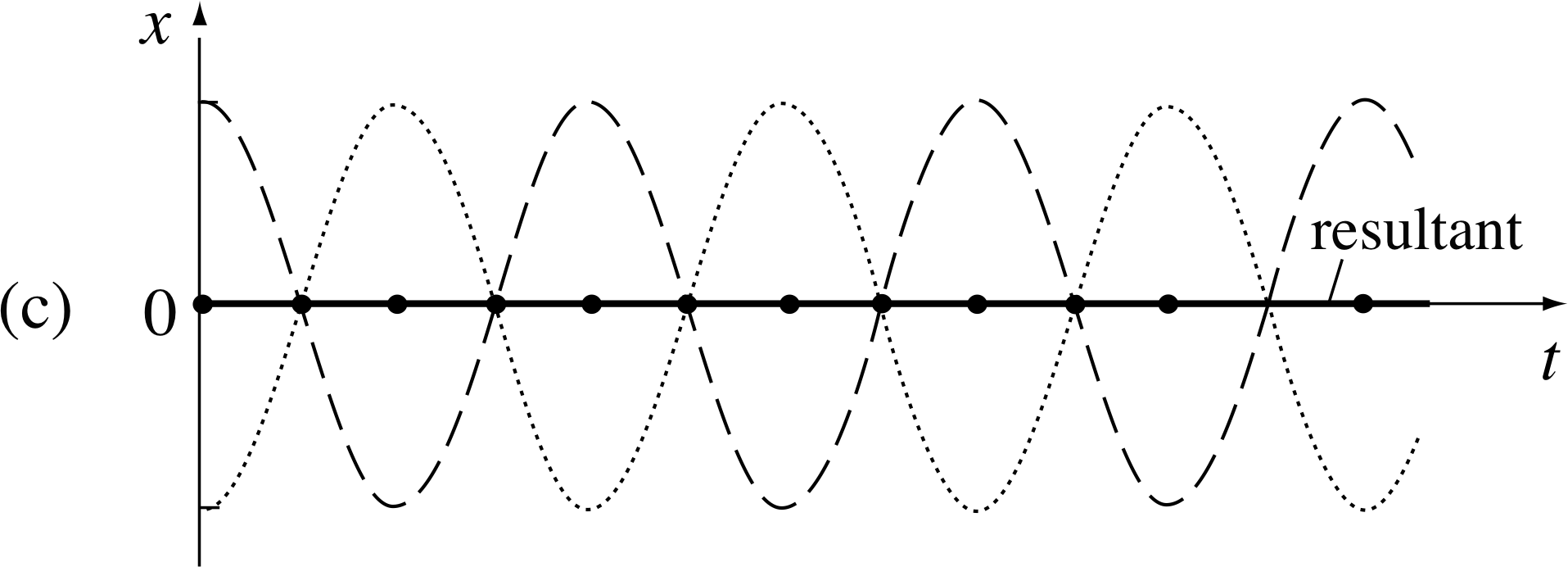
Figure 12c Superposition of two SHMs of the same amplitude and frequency and in anti-phase
Superposing two SHMs that differ only in phase gives
x (t) = A cos(ωt + ϕ1) + A cos(ωt + ϕ2)(24a)
A standard trigonometric identity gives the result of adding two cosines like this. i Using that identity we can write Equation 24a as
$x(t) = 2A\cos\left(\dfrac{\omega t+\phi_1-\omega t - \phi_2}{2}\right)\cos\left(\dfrac{\omega t+\phi_1+\omega t + \phi_2}{2}\right)$
i.e.$x(t) = 2A\cos\left(\dfrac{\phi_1 - \phi_2}{2}\right)\cos\left(\omega t + \dfrac{\phi_1+ \phi_2}{2}\right)$(25a)
Since $\cos\left(\dfrac{\phi_1 - \phi_2}{2}\right)$ is a constant, Equation 25a can be interpreted as a new SHM of angular frequency ω (the same as before) but of amplitude $2A\cos\left(\dfrac{\phi_1 - \phi_2}{2}\right)$ and phase constant (ϕ1 + ϕ2)/2, which is the mean phase constant for the two oscillations.
We can pick out two special cases:
-
When the two oscillations are in phase, i.e. when ϕ1 = ϕ2 so that (ϕ1 − ϕ2) = 0. In this case we can set ϕ1 = ϕ2 = ϕ and Equation 25abecomes
x (t) = 2A cos(ωt + ϕ)(26a)
which corresponds to a simple oscillation of twice the original amplitude. Sometimes this situation is described as fully constructive superposition (Figure 12a).
-
When the two oscillations are in anti-phase, i.e. when | ϕ1 − ϕ2 | = π. In this case Equation 25a becomes x (t) = 0, and there is no oscillation. Sometimes this situation is described as fully destructive superposition (Figure 12c).
For the general case, where the phase difference lies between the two extremes of in phase and in anti-phase the superposition can be represented as in Figure 12b.
Superposition of two equal amplitude SHMs
If we replace the common value of ω in Equation 24a,
x (t) = A cos(ωt + ϕ1) + A cos(ωt + ϕ2)(Eqn 24a)
by two separate values ω1 and ω2 we obtain
x (t) = A cos(ω1t + ϕ1) + A cos(ω2t + ϕ2)(24b)
The addition of the two cosines now gives
$x(t) = 2A\cos\left(\dfrac{\omega_1 t+\phi_1-\omega_2 t - \phi_2}{2}\right)\cos\left(\dfrac{\omega_1 t+\phi_1+\omega_2 t + \phi_2}{2}\right)$(25a)
i.e.$x(t) = 2A\cos\left[\dfrac{(\omega_1-\omega_2)t}{2}+\dfrac{(\phi_1 - \phi_2)}{2}\right]\cos\left[\dfrac{(\omega_1+\omega_2)t}{2}+\dfrac{(\phi_1 + \phi_2)}{2}\right]$(25b) i
Equation 25b has no easy interpretation except in the special case where ω1 and ω2 are fairly similar. In this case | ω1 − ω2 | ≪ (ω1 + ω2) and the first cosine function is a slowly varying function of time, as compared with the rapidly varying second cosine function.
Figure 13 Superposition of two colinear SHMs of the same amplitude acting in the same direction but differing in angular frequency in the ratio 13 : 11.
The superposition is then a new kind of oscillation, similar to SHM, in which displacement varies over time at the average frequency, fav = (ω1 + ω2)/4π, with the average phase constant, (ϕ1 + ϕ2)/2, but having an ‘amplitude’ which varies slowly with time at the difference frequency, fdiff = | ω1 − ω2 |/4π with the difference phase constant, (ϕ1 − ϕ2)/2.
The displacement – time graph of this superposition of SHMs is shown in Figure 13 for the case where the two equal amplitude original oscillations have frequencies in the ratio 13 : 11.
The slow periodic amplitude oscillations are referred to as beats. The beat frequency is equal to | ω1 − ω2 |/2π. i Beats are most pronounced when SHMs of equal amplitude are superposed, but they are also observable when the amplitudes are similar but not equal.
Superposition of two colinear SHMs in the general case
Now we return to the general case of Equation 24,
x (t) = A1 cos(ω1t + ϕ1) + A2 cos(ω2t + ϕ2)(Eqn 24)
To simplify our notation here we will write the phase (ω1t + ϕ1) as θ1(t) and the phase (ω2t + ϕ2) as θ2(t) so that Equation 24 can be written as
x (t) = Α1cos θ1(t) + A2cos θ2(t)
Inspired by our earlier finding (Equation 25b) that the superposition of two SHMs can result in a motion that is similar to SHM albeit with a time dependent ‘amplitude’ we will now assume that the result of superposing two general SHMs can be represented by an equation of the form
x (t) = A (t) cos θ (t)
where A (t) and θ (t) are the resulting amplitude and phase with x (t) as the displacement.
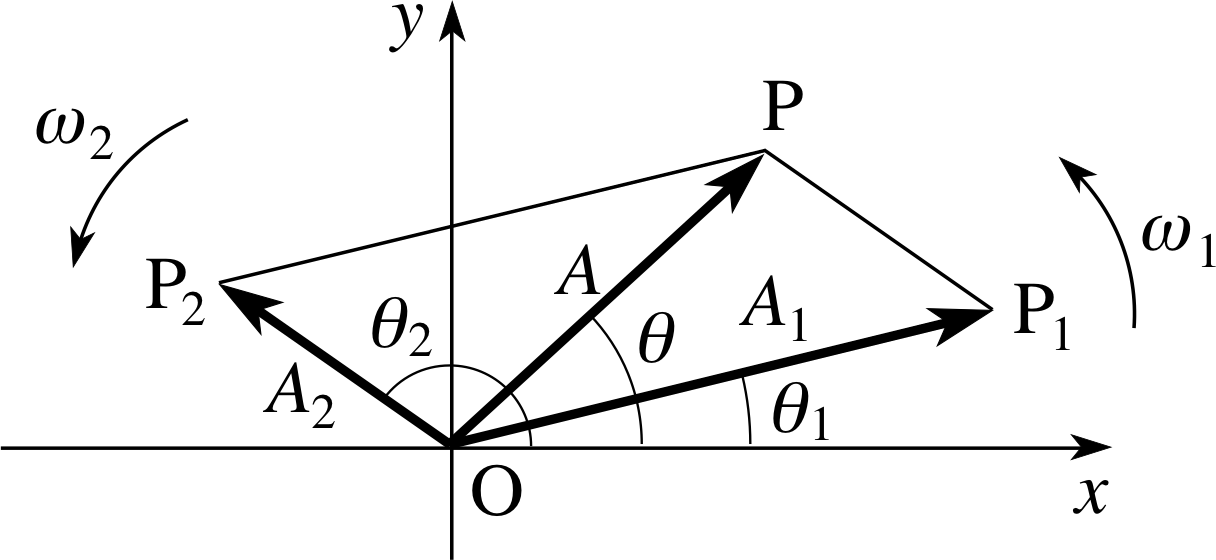
Figure 14 Phasor diagram for the SHMs acting in the same direction.
In order to work out A (t) and θ (t) we will represent both of the original y oscillations by rotating phasors, as in Figure 14. The first phasor has a constant amplitude Α1 and a phase θ1(t) and is represented at time t by the line $\overrightarrow{OP_1}$, while the second phasor, which has amplitude A2, is shown by $\overrightarrow{OP_2}$. The addition of these two phasors can be treated in an analogous way to the addition of two vectors – by a triangle rule or a parallelogram rule to produce the resultant phasor $\overrightarrow{OP}$. As $\overrightarrow{OP_1}$ and $\overrightarrow{OP_2}$ each rotate anti–clockwise at different angular speeds it is clear that their instantaneous sum $\overrightarrow{OP}$ will rotate in a complicated way and with a varying length or amplitude. This justifies our assumption above.
At any time t, the x and y components of $\overrightarrow{OP}$ are
x (t) = A (t) cos θ (t) = A1cos θ1(t) + A2cos θ2(t)(26)
y (t) = A (t) sin θ (t) = A1 sin θ1(t) + A2sin θ2(t)(27)
To find A (t) we square and add Equations 26 and 27 and then take the positive square root to obtain: i
$A(t) = \sqrt{\smash[b]{A_1^2 +A_2^2 + 2A_1A_2\cos\left[\theta_1(t)-\theta_2(t)\right]}}$(28)
To find the resultant phase θ (t) we divide Equation 27 by Equation 26 to give tan θ (t) = sin θ (t)/cos θ (t) and then
$\theta(t) = \arctan\left[\dfrac{A_1\sin\theta_1(t) + A_2\sin\theta_2(t)}{A_1\cos\theta_1(t) + A_2\cos\theta_2(t)}\right]$(29)
Equation 29 always has two solutions, differing by 180°; the appropriate solution can be selected by considering the phasor diagram.
Question T13
Two colinear SHMs of the same frequency are superposed. The amplitudes are A1 = 2 mm and A2 = 1 mm and at time t = 0 the phases are θ1(0) = ϕ1 = −120° and θ2(0) = ϕ2 = 30°. Calculate the amplitude and phase of the resulting disturbance at t = 0.
Answer T13
From Equation 28,
$A(t) = \sqrt{\smash[b]{A_1^2 +A_2^2 + 2A_1A_2\cos\left[\theta_1(t)-\theta_2(t)\right]}}$(Eqn 28)
$A = \rm \sqrt{2^2+1^2+(2\times1\times2)\cos(-150°)}\,mm = 1.24\,mm$
From Equation 29,
$\theta = \arctan\left(\dfrac{A_1\sin\theta_1 + A_2\sin\theta_2}{A_1\cos\theta_1 + A_2\cos\theta_2}\right)$(Eqn 29)
If we set time t = 0 then all these θs become ϕs and we have
$\phi = \arctan\left[\dfrac{2\sin(-120°) + \sin(30°)}{2\cos(-120°) + \cos(30°)}\right]$
sin 60° = cos 30° = $\sqrt{3\os}/2$ and sin 30° = cos 60° = 1/2, therefore
$\phi = \arctan\left(\dfrac{0.5 - \sqrt{3\os}}{0.5\sqrt{3\os}-1}\right)$
ϕ = 83.8° or (83.8° − 180°) = −96.2°
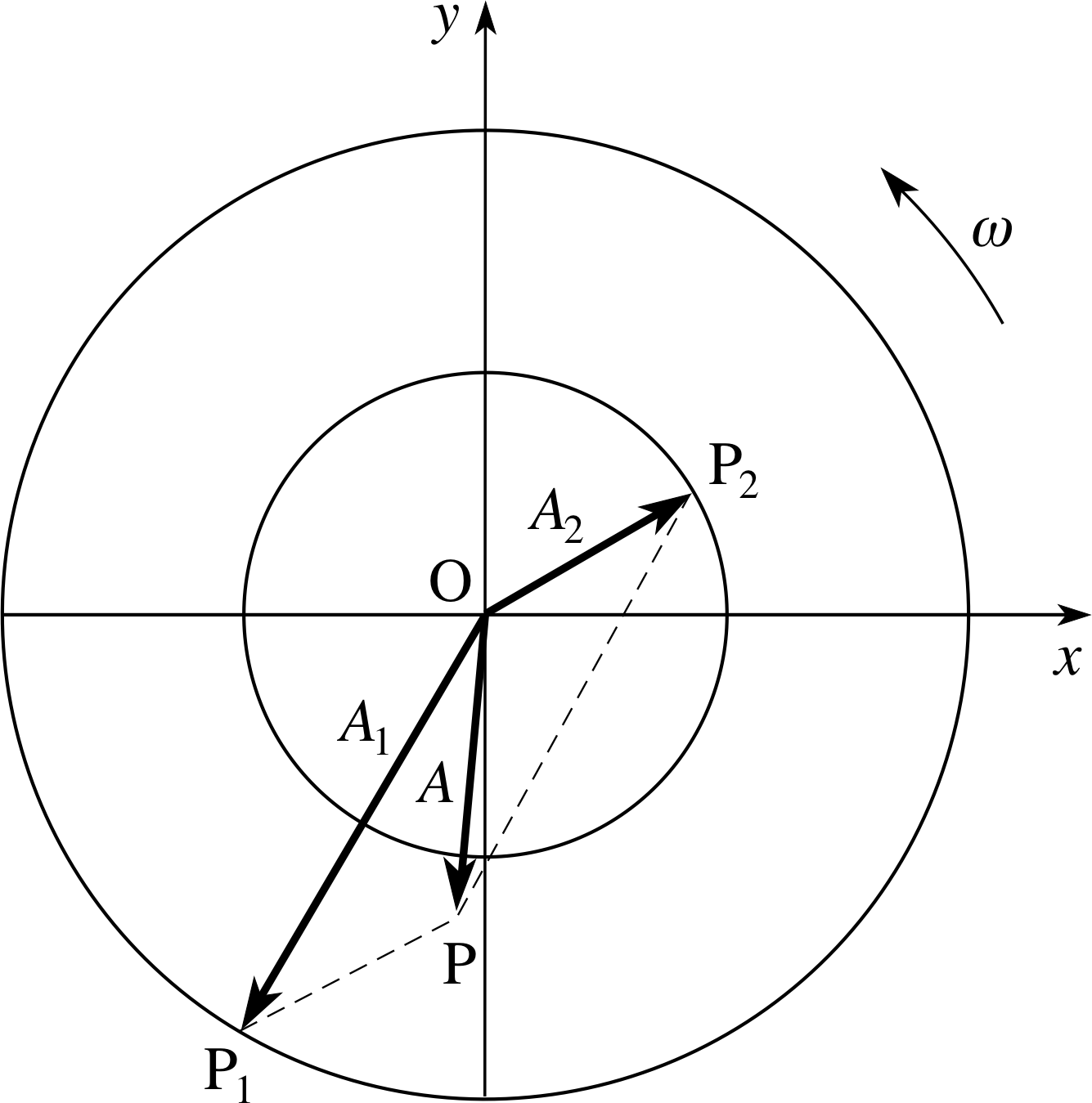
Figure 23 See Answer T13.
Notice that there is an ambiguity in the value of ϕ given by tan ϕ. This has been introduced by the arctan function
in Equation 29, which has two solutions within the range 180° > ϕ > −180°. Had we worked directly with the sine and cosine expressions (Equations 26 and 27)
x (t) = A (t) cos θ (t) = A1cos θ1(t) + A2cos θ2(t)(Eqn 26)
y (t) = A (t) sin θ (t) = A1sin θ1(t) + A2sin θ2(t)(Eqn 27)
this would not have arisen but we would still have had to choose the correct angle to give both sine and cosine negative – this gives us the ϕ = −96.2° solution.
Perhaps a more instructive approach is to sketch the phasor addition diagram, shown in Figure 23, from which the correct angle is obvious.
Equations 28 and 29 include the results for the less general cases covered by Equations 25a and 25b,
$x(t) = 2A\cos\left(\dfrac{\omega_1 t+\phi_1-\omega_2 t - \phi_2}{2}\right)\cos\left(\dfrac{\omega_1 t+\phi_1+\omega_2 t + \phi_2}{2}\right)$(25a)
$x(t) = 2A\cos\left[\dfrac{(\omega_1-\omega_2)t}{2}+\dfrac{(\phi_1 - \phi_2)}{2}\right]\cos\left[\dfrac{(\omega_1+\omega_2)t}{2}+\dfrac{(\phi_1 + \phi_2)}{2}\right]$(25b)
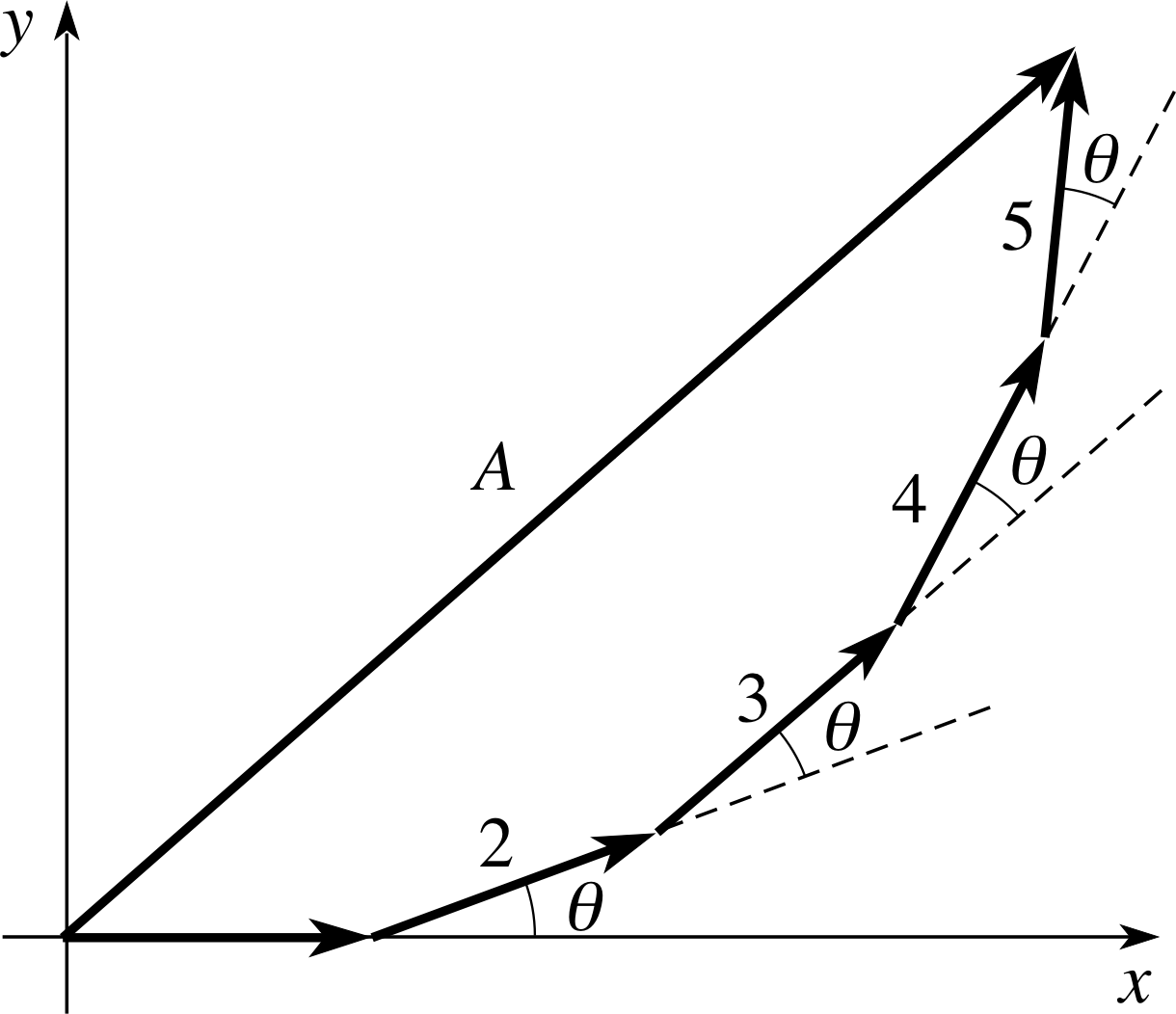
Figure 15 Phasor addition of five SHMs all of the same amplitude and frequency but with a fixed phase angle between successive contributions.
While the analytic solution of problems such as these is quite complex, the phasor addition diagram gives a powerful visualization of the process.
Having superposed two SHMs, we can go on to superpose a third SHM on the resultant of these two to form the resultant of three SHMs, and so on. By continuing this procedure we can superpose any number of SHMs. For multiple additions the phasor diagram approach is by far the simplest one. Perhaps the most spectacular examples are found in optics where investigating the effect of many light waves arriving at a common point can lead us to superpose many oscillations, all in the same direction and all of the same frequency but with different phase constants. In such cases the analytic solution becomes very complicated while the phasor approach remains clear and helpful. Figure 15 shows an example of multiple superpositions of the type found in optics. It shows the phasor addition of five SHMs, all of the same frequency but with a fixed phase angle.
Question T14
A guitar string of length 0.67 m is sounded together with a tuning fork. In the ear the oscillations from these two sources are superposed and a beat frequency of 5 beats per second is heard. The string is gradually shortened and the beat frequency decreases until, at a length of 0.66 m, it is down to 2 beats per second. Assuming the frequency produced by the string to be inversely proportional to its length, calculate the frequency of the tuning fork. i
Answer T14
Let the fork frequency be f, the first string frequency f1 and the second string frequency f2. From the beats we know that
| f1 − f | = 5 and | f2 − f | = 2
Since we are told that the frequency is inversely proportional to the length, we know that f2 > f1. Since the string frequency is brought nearer to that of the fork when it is increased to f2 this implies that f must be higher than either f1 or f2 and, assuming that there is no lower beat at any frequency between f1 and f2, our beat conditions are
(f − f1) = 5 and (f − f2) = 2 (i.e. f1 = f − 5 and f2 = f − 2)
Sincef1/f2 = l2/l1 = 0.66/0.67
or0.67f1 = 0.66f2
we have0.67 (f − 5) = 0.66 (f − 2)
andf = [(5 × 0.67) − (2 × 0.66)]/0.01 = 203 Hz
3.2 Superposition of perpendicular SHMs: independent and coupled oscillators

Figure 1 Two simple oscillators in their equilibrium positions.
Our discussion so far has been confined to SHM in one physical dimension. However, oscillations can occur in two, or three physical dimensions. For example, the simple pendulum in Figure 1b is a three–dimensional oscillator, because it can swing from north to south or east to west – and it also moves up and down to a lesser extent. It can execute all these motions simultaneously, so that the general motion of the bob is a complex path in space. If we were to look from above or below we would see the bob tracing out a path in a horizontal plane (the (x, y) plane, say) while from the side we would also see the vertical motion. The matter does not end here. In addition to these swinging motions there could be twisting motion around the thread; this so–called torsional motion can also be shown to be SHM (although we will not do so in this module). Taken together, the pendulum may be subject to four independent oscillations simultaneously.
These independent motions of an oscillator are called the modes of vibration of the oscillator and their number is called the number of degrees of freedom of the oscillator. In this case there are four modes of vibration, including three swinging modes and one torsional mode, and there are therefore four degrees of freedom.
You will appreciate that when all these modes are in action together, the task of predicting the position of a particular point on the bob is quite challenging! Fortunately, the task is made much simpler if we know that the various motions are truly independent.
The condition for independent oscillators is that the oscillators are unaware of each other – either because they are remote from each other or because the displacement of one does not affect the forces and hence motions of the others. In our case here, each of the degrees of freedom represents an independent oscillator. We can be confident of this with our pendulum since the restoring forces in the swinging modes depend on the weight of the bob and this is independent of where the bob is placed. i The torsional mode is controlled by the physical properties of the thread, (i.e. its rigid_bodyrigidity) not at all by gravity, and so this mode is independent of the others. If two oscillators or two modes of a single oscillator are not independent, they are said to be coupled_oscillatorscoupled.
We could have had this same discussion in relation to the mass on the spring, as shown in Figure 1a. This system can oscillate up and down and it can swing and twist like the pendulum. In general, it is important to develop a means of combining independent oscillations. We will do this only in the case of two independent, perpendicular SHMs.
Figure 16 Phasor diagram of the superposition of two perpendicular oscillations.
We can use the phasor model again to picture the result of superposing two perpendicular SHMs. Figure 16 shows the general case for the superposition of two phasors $\overrightarrow{OP_1}$ and $\overrightarrow{OP_2}$. These have different amplitudes, phases and, possibly, different frequencies. We consider $\overrightarrow{OP_1}$ as generating the x–motion (point Q1) and $\overrightarrow{OP_2}$ as generating the y–motion (point Q2). The result of the superposition at any particular time is represented by the point P, which has its x and y–coordinates determined by Q1 and Q2, respectively. The path traced by P, as P1 and P2 rotate, represents the motion of an object which is subject to these two perpendicular motions.
The moving point P in Figure 16 might, for example, represent the motion of a pendulum bob in the (x, y) plane, as it would be seen from above. Here we would use the same frequency for the x and y motions (determined by the length of the pendulum), even though their amplitudes and phase constants might differ. The path of the bob would in general be an ellipse, but could be long and thin or short and fat – it would be circular if the x and y motions had the same amplitude or, in the limit where one amplitude is zero, it would be a simple one–dimensional motion along either x or y–axes.
Of course, the shape of the path in the (x, y) plane is a purely geometrical result, and there remain significant questions to be asked, about the speed and direction of motion at different points on the trajectory. These considerations are outside the scope of this module but they too can be handled by phasor methods.
Approaching the general two–dimensional problem analytically, we can represent the x and y–components of the two–dimensional displacement at time t by
x (t) = A1 cos ω1t(30a)
y (t) = A2 cos(ω2t + ϕ)(30b) i
Figure 18 Lissajous figures from two perpendicular one–dimensional oscillations at different frequencies. In these examples, A1 = A2; but the ratio ω2 : ω1 varies from row to row and the phase constant ϕ varies from column to column. (These curves are generated from Equations 30a and 30b, with A1 = A2).
in which the zero of time has been chosen to coincide with the positive turning point of the x–motion at x = A1. These equations give the trajectory followed by the object in the (x, y) plane in terms of the time t. If we eliminate t between these two equations we find the equation of the trajectory – that is an expression for y in terms of x.
These trajectories are known as Lissajous figures and several such figures are shown, for various amplitudes, frequencies and phase constants in Figure 17 and Figure 18.
Figure 17 Lissajous figures from the two–dimensional oscillations of a simple pendulum. Each ellipse is tagged with the value of ϕ to which it corresponds: (a) with equal amplitudes, (b) when A1/A2 = 1.5. (The curves are generated from Equations 30a and 30b, with ω1 = ω2).
Question T15
A pendulum swings in the (x, y) plane such that the oscillations in the x and y–directions have amplitudes in the ratio of 1 : 2 and the larger amplitude oscillator (in y) leads the other by π/4. Sketch the corresponding Lissajous figure.
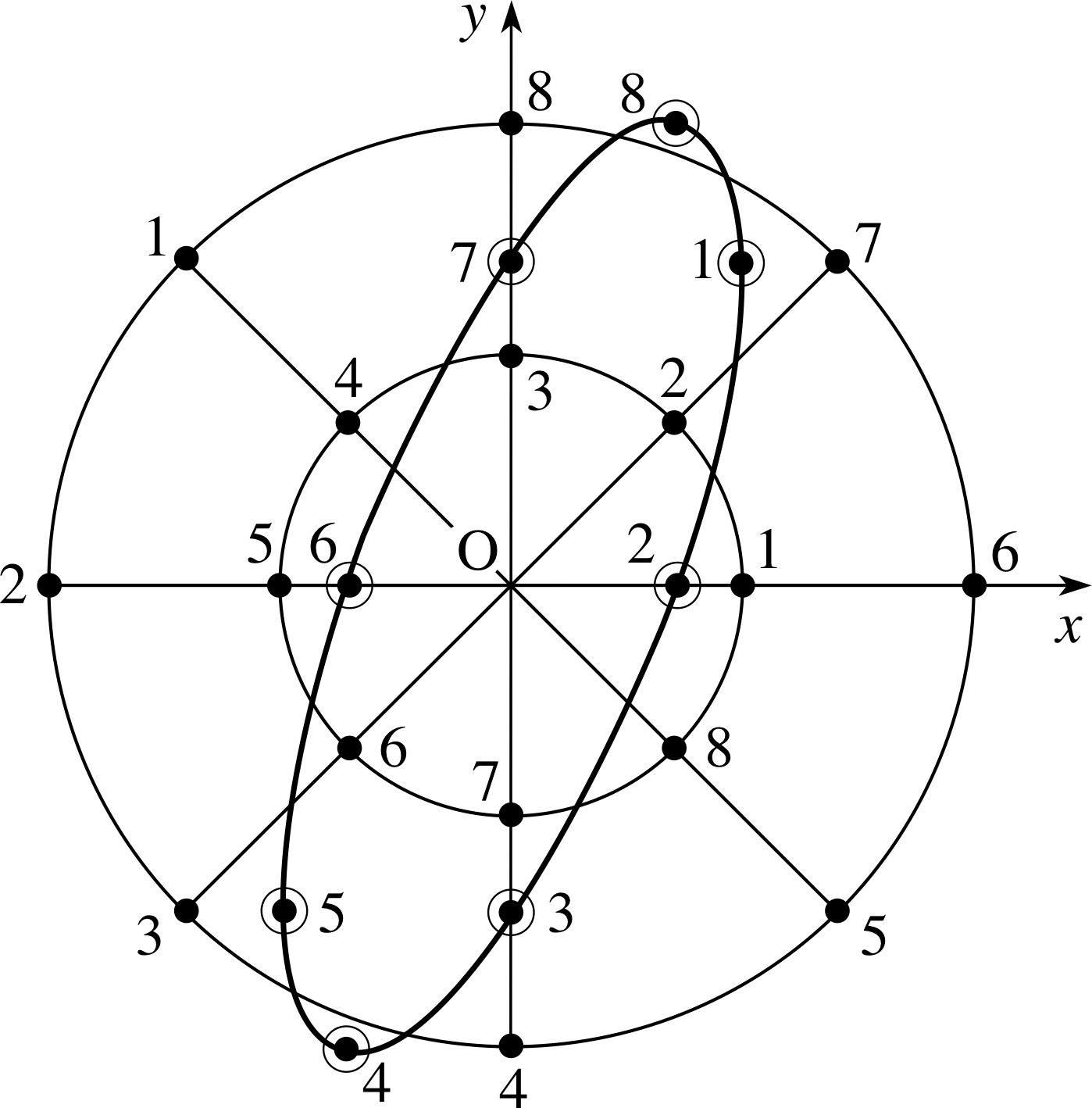
Figure 24 See Answer T15.
Answer T15
The frequencies of the two oscillators here are the same, since they are both determined by the length of the pendulum. Figure 24 shows the Lissajous figure for the motion. This has been constructed by taking eight successive ‘snapshots’ of the phasor diagram throughout one full cycle (with phasors and resultant positions numbered 1 to 8). The path of the resultant motion is represented by the ellipse.
4 Closing items
4.1 Module summary
- 1
-
When a system in stable equilibrium is disturbed slightly, it is subject to a restoring force which tends to direct it back towards its position of equilibrium, and the system, therefore, oscillates about that position.
- 2
-
SHMSimple harmonic motion (SHM) may be characterized in one dimension by the equation
x (t) = A cos(ωt + ϕ)(Eqn 6a)
where x (t) represents the displacement from the equilibrium position at time t, A is the amplitude of the motion, ω is its angular frequency and ϕ is the phase constant. It follows from this equation that the acceleration at time t is given by
ax(t) = −ω2 x (t)(Eqn 12)
and it follows from this that the force required to sustain such motion must be
Fx(t) = −mω2x (t) = −kx (t)(Eqn 13)
- 3
-
The period T = 2π/ω = 1/f of SHM is independent of the amplitude of the motion.
- 4
-
Analysis of the forces operating in simple stable systems verifies that they are of the form Fx = −kx, where x is the displacement and k is a constant. This explains why simple harmonic motion is the natural state of oscillation of stable systems, where the restoring forces can be treated as linearly dependent on displacement.
- 5
-
If the amplitude of an oscillator is not sufficiently small, the restoring forces cease to be linearly proportional to the displacement and the simple behaviour, characteristic of SHM, is lost. In these anharmonic oscillations the period is usually dependent on the amplitude.
- 6
-
Uniform circular motion provides a convenient model for SHM. The projected motion along any diameter mimics that of one–dimensional SHM. The model gives a visual interpretation of phase and angular frequency.
- 7
-
A phasor model more formally represents the amplitude and phase of SHM and also allows the addition or superposition of several such motions, either in the same direction or in perpendicular directions.
- 8
-
Independent oscillators are ones in which the displacement of one does not change the restoring forces acting on the others. Coupled oscillators are those in which these mutual effects are present.
- 9
-
If oscillations of similar frequency and amplitude are superposed in the same direction, the phenomenon of beating is observed.
- 10
-
When two independent perpendicular oscillations are superposed, the path of the resultant motion is described by a Lissajous figure.
4.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Account for and describe, qualitatively, the oscillations of a stable system and relate frequency, angular frequency and period.
- A3
-
Sketch displacement–time, velocity–time and acceleration–time graphs for SHM, explain how they are related and construct the second two from the first.
- A4
-
Write down a general algebraic expression for the displacement in SHM, use this to derive expressions for the velocity and the acceleration, and use these three to solve problems in SHM.
- A5
-
Show that SHM is governed by an acceleration and a restoring force which are both linear in the displacement.
- A6
-
Analyse simple stable systems, and calculate their periods of oscillation.
- A7
-
Describe how anharmonic oscillations arise in a system and explain how these differ from SHM.
- A8
-
Describe and obtain formulae for the superposition of two colinear SHMs, and explain these results in relation to the phasor model.
- A9
-
Describe and explain the phenomenon of beats.
- A10
-
Describe and obtain general formulae for the superposition of two independent perpendicular SHMs, and explain these results in relation to the phasor model.
- A11
-
Describe and construct simple Lissajous figures for the superposition of two perpendicular SHMs.
Study comment You may now wish to take the Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A3)
The bob of a simple pendulum is moved to one side and released from rest. Sketch the displacement–time graph for the subsequent motion. How does the velocity–time graph differ from this?

Figure 5 Graphs of the displacement, velocity and acceleration for an object in one–dimensional SHM, as represented by Equations 6a, 9a and 10a, with ϕ = 0.
Answer E1
This oscillation starts at maximum displacement and it is therefore a simple cosine function, with zero phase constant. Figures 5a and b show the displacement–time and velocity–time graphs and the velocity leads the displacement by π/2.
(If you had difficulty with this question reread Subsection 2.4.)
Question E2 (A2)
If the frequency of a particular SHM is 50 Hz, what is the angular frequency and the period?
Answer E2
The angular frequency
ω = 2πf = (2π × 50) rad s−1 = 100π rad s−1
and the period
T = 2π/ω = 1/f = (1/50) s = 0.02 s
(If you had difficulty with this question reread Subsection 2.2.)
Question E3 (A1 and A8)
Two equal amplitude oscillators of the same frequency differ in phase by 60°. Explain what this statement means, with the aid of a sinusoidal sketch and also in terms of a phasor diagram. Indicate on your sketches which oscillator leads.
Figure 25b See Answer E3.
Figure 25a See Answer E3.
Answer E3
The two oscillations
x1 = A cos ωt
andx2 = A cos(ωt − π/3)
differ by π/3 (60°) with x1 leading x2. Figure 25a shows this situation (a) on a sinusoidal graph and (b) on a phasor diagram. Notice that x1 leads x2 because x1 reaches its maximum before x2 reaches its maximum (i.e. at an earlier time).
(If you had difficulty with this question reread Subsections 2.2, 2.4 and 2.5.)
Question E4 (A4)
A pendulum of period 10 s has, initially, a displacement of 1 m and a velocity of 2.5 m s−1. Find an algebraic expression for the displacement.
Answer E4
Using Equations 6a and 9a,
$x(t) = A\cos\left(\dfrac{2\pi t}{T}+\phi\right) = A\cos(\omega t+\phi)$(Eqn 6a)
υx (t) = −Aωsin(ωt + ϕ)(Eqn 9a)
and putting in the initial conditions for x and υx at t = 0, with ω = 2π/T = π/5, we find
1 = A cos ϕ and $2.5 = -\dfrac{A\pi\sin\phi}{5}$
so$\tan\phi = \dfrac{\sin\phi}{\cos\phi} = \dfrac{-12.5}{A\pi} = -3.98$
This gives ϕ = −76° or −1.32 rad and A = 1/cos ϕ = 4.1 m
Finally, the expression for x is
$x(t) = 4.1\cos\left(\dfrac{\pi}{5} - 1.32\right)$
(If you had difficulty with this question reread Subsections 2.3 and 2.4.)
Question E5 (A4 and A5)
Starting from an expression for the displacement in SHM, show that the acceleration and the restoring force are each proportional to this displacement.
Answer E5
Refer to Subsection 2.4 and, in particular, to Equations 6a, 9a, 10a and 11; also to Subsection 2.6, Equation 13,
$x(t) = A\cos\left(\dfrac{2\pi t}{T}+\phi\right) = A\cos(\omega t+\phi)$(Eqn 6a)
υx ( t ) = − Aωsin(ω t + ϕ )(Eqn 9a)
ax (t) = −Aω2 cos(ωt + ϕ)(Eqn 10a)
ax (t) = −Aω2 cos(ωt + ϕ) = −ω2x (t)(Eqn 11a)
ax (t) = −Aω2sin(ωt + ϕ) = −ω2x (t)(Eqn 11b)
Fx(t) = max(t) = −mω2x (t)(Eqn 13)
Question E6 (A6)
A 5.0 kg mass is attached to the lower end of a spring whose force constant is 4.0 × 102 N m−1. The mass is then pulled down 5 cm below the position of equilibrium and released from rest. Calculate the period of oscillation if the experiment is conducted: (a) on the Earth’s surface, where g = 9.8 m s−2, (b) on the Moon’s surface, where g = 1.6 m s−2, (c) in a region of space where there is no gravity.
Answer E6
Refer to Answer T9 for the general approach. Using Equation 16,
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac mk}$(Eqn 16)
For (a), (b) and (c)
$T = 2\pi\sqrt{\dfrac{\rm 5.0\,kg}{\rm 4.0\times10^2\,N\,m^{-1}}} = 2\pi\sqrt{\dfrac{\rm 1.25\times10^{-2}\,kg}{\rm kg\,m\,s^{-2}\,m^{-1}}} = 0.70\,{\rm s}$
This period is independent of the amplitude (assuming SHM) and of the acceleration of gravity – it depends on the mass of the mass attached to the spring but not on the weight of the mass! If we were to build a clock based on this oscillator it would keep good time in all these locations.
(If you had difficulty with this question reread Subsections 2.6 and 2.7.)
Question E7 (A6)
A 5.0 kg mass is attached to the lower end of a wire of length 1.5 m and is then drawn aside and released. Calculate the period of oscillation if the experiment is conducted: (a) on the Earth’s surface, where g = 9.8 m s−2, (b) on the Moon’s surface, where g = 1.6 m s−2, (c) in a region of space where there is no gravity.
Answer E7
Equation 22,
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac Lg}$(Eqn 22)
tells us that the mass of the bob is irrelevant here, only the length of the pendulum and the acceleration of gravity are involved. We find:
(a) on the Earth
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac Lg} = 2\pi\rm\sqrt{\dfrac{1.5\,m}{9.8\,m\,s^{-2}}} = 2.5\,s$
(b) on the Moon
$T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac Lg} = 2\pi\rm\sqrt{\dfrac{1.5\,m}{1.6\,m\,s^{-2}}} = 6.1\,s$
(c) in space there will be no restoring force and hence no oscillation.
You might have suspected that the pendulum would not swing very well without some gravity – gravity is a serious business for such a clock!
(If you had difficulty with this question reread Subsections 2.6 and 2.7.)

Figure 24 See Question E8.
Question E8 (A8 and A9)
A vibrating string produces two colinear oscillations, with a frequency ratio of 1 : 2. The higher frequency oscillation has only one–third of the amplitude of the other oscillation. Starting from a time when the two oscillations are in phase, show on a phasor diagram the superposed displacement over one full cycle of the lower frequency oscillation. [Hint: though the details differ, you may find it helpful to consider Figure 24 before attempting this question.]
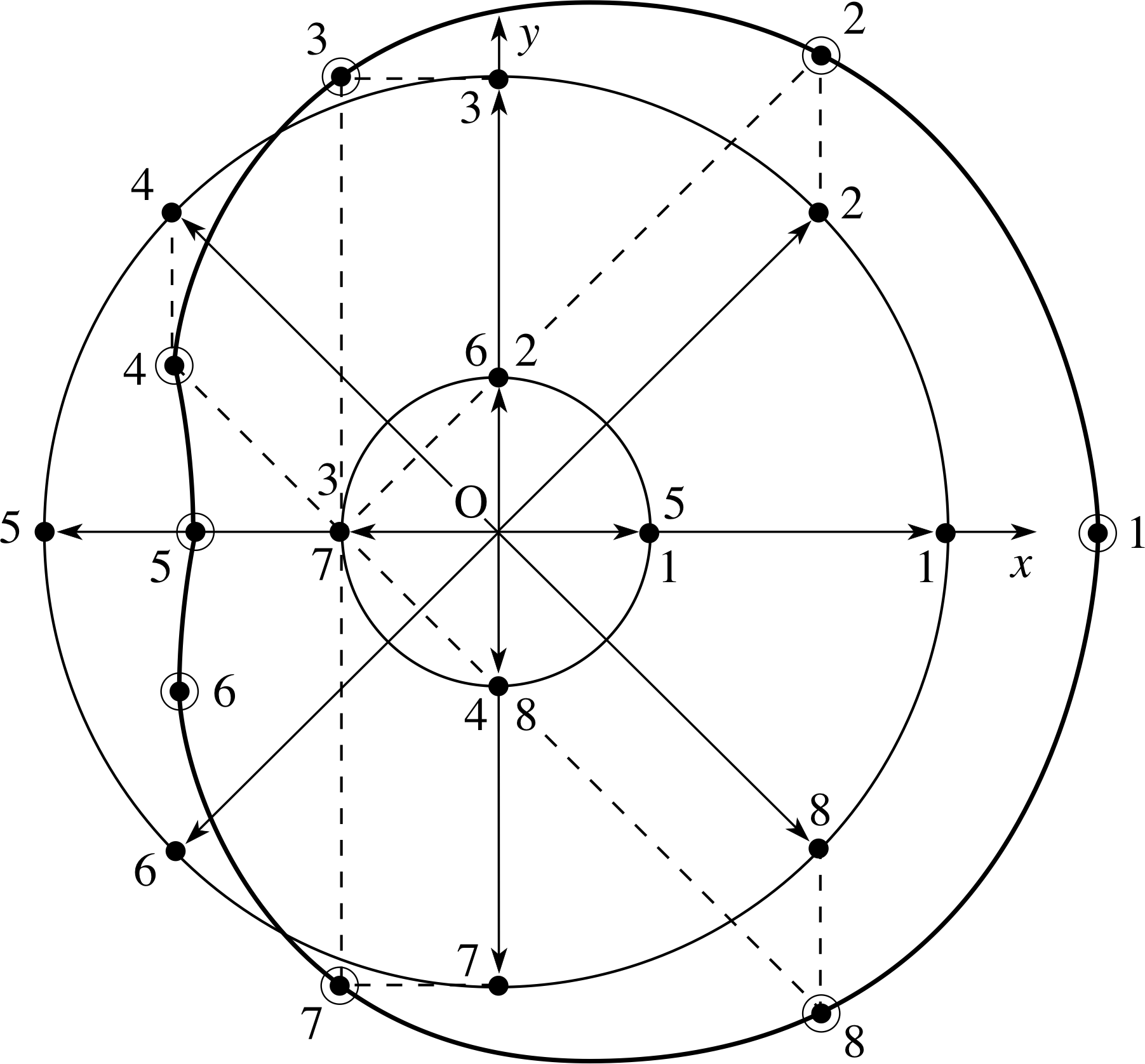
Figure 26 See Answer E8.
Answer E8
Figure 26 shows the phasor diagram for the superposition of two oscillations with a frequency ratio 1 : 2 and an amplitude ratio 3 : 1, both acting in the same dimension. This has been constructed by taking eight successive ‘snapshots’ of the diagram throughout one full cycle of the lower frequency oscillation (with phasors and resultant positions numbered 1 to 8).
(If you had difficulty with this question reread Subsection 3.2.)
Question E9 (A7)
Explain the circumstances under which anharmonic oscillations may occur and explain how they might be identified as such.
Answer E9
Anharmonic oscillations occur whenever a stable system is displaced from equilibrium and the restoring force is non–linear in the displacement. This is discussed in Subsection 2.8.
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 4Closing items.