PHYS 2.4: Work and energy |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Energy is one of the fundamental concepts of physics. In the context of Newtonian mechanics it often provides a simple way of solving problems that would be very difficult to solve directly in terms of forces and accelerations. An example of this is given at the end of this module, where you will see how easy it is to determine the minimum speed with which a projectile must be launched if it is to escape entirely the gravitational attraction of an airless body such as the Moon.
Section 2 introduces the concept of the work done on a body by a force. A vector approach is used to show how the work done can be quantified in various three–dimensional situations, including those in which the force changes its magnitude and direction during the displacement and the expression for the work done involves an integral. (Although integrals appear throughout this module, the concept of integration and its relationship to the area under a graph is introduced in Section 2, and familiarity with the mathematical techniques of integration is not a prerequisite.) This section also introduces the concept of (translational) kinetic energy and explains how changes in this quantity can sometimes be related to the work done on a body.
Section 3 deals with the idea of conservative and non-conservative forces and introduces the concept of potential energy in relation to the former. It shows that in an isolated system the total mechanical energy is conserved, whereas, when non–conservative forces act, mechanical energy is not conserved. The extension of this idea to embrace all forms of energy, including the energy associated with mass, leads to the principle of conservation of energy. This asserts that in an isolated system the total energy is constant. Although energy can be converted from one form into another, it cannot be created nor destroyed. In this section also, the important relationship between a conservative force and the associated potential energy is introduced (Fx = −dEpot/dx).
Section 4 considers power, as the rate of doing work and Section 5 includes applications of the concept of energy to collisions and to the calculation of escape speeds.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 6.1Module summary and the Subsection 6.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 6.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
During a road accident, a car slides 130 m with locked wheels. If the magnitude of the frictional force between the tyres and the road is 0.80 × the magnitude of the weight of the car, calculate the speed of the car at the moment the brakes are applied. Take g = 9.81 m s−2.
Answer F1
If the mass of the car is m, then the magnitude of the frictional force is f = 0.8mg. The frictional force is opposed to the direction of motion, so the work done in bringing the car to rest at a distance s is fs cos θ = −0.8mgs. This must be equal to the change in the translational kinetic energy of the car,
(Etran)f − (Etran)i = 0 − ½ mυ2 = −½ mυ2
Thus0.8mgs = ½ mυ2
so$\upsilon = \sqrt{1.60gs\os} = \rm \sqrt{1.60\times 9.8\,m\,s^{-2}\times 130\,m} = 45.2\,m\,s^{-1}$
This is 101 mph! The driver is in trouble.
Question F2
Derive an expression for the (minimum) escape speed required for a projectile to leave the surface of a planet and escape entirely from its gravitational attraction. Calculate the value of this speed for the planet Jupiter, which has a mass of 1.90 × 1027 kg and a radius of 71.5 × 106 m. (Newton’s gravitational constant G = 6.67 × 10−11 N m2 kg−2).
Answer F2
The expression for escape speed υes is derived using the principle of conservation of mechanical energy and the general expression for gravitational potential energy. Full details are given in Subsection 5.2, where Equation 38,
υes = (2GME/RE)1/2(Eqn 38)
implies:
υes = (2GM/R)1/2
Putting in the given values of G, M and R, we find
υes = 59.5 × 103 m s−1
Question F3
One end of a light spring is fixed to a ceiling so that the other (free) end hangs directly below it when the spring is in its normal unextended state. A downward pointing x–axis is chosen so that the free end of the unextended spring is at x = 0 and any further downward extension corresponds to a positive value of x. A 1 kg block is added to the free end, causing an extension x = 0.10 m when the block is in equilibrium. The block is pulled down a further 0.20 m and then released. The spring has a special property. For any extension, x, the applied force required to maintain the spring in equilibrium is Fx = ksx3. Find the speed of the block as it passes through its former equilibrium position. (If you are not familiar with the techniques of integration you will find it useful to know that the area under the graph of F against x, between x = 0 and x = x is $\frac 14 k_s x_{\rm max}^4$). Take g = 9.81 m s−2.
Answer F3
First it is necessary to derive an expression for the potential energy of this special spring. Since the applied force Fx = ksx3, the work done by this force in stretching the spring from 0 to some fixed value xmax will be:
$\displaystyle W = \int_0^{x_{\rm max}}k_sx^3\,dx$
This definite integral represents the area under the graph of Fx against x between x = 0 and x = xmax. Using the information given in the question (or by evaluating the integral) it follows that:
$\displaystyle W = \int_0^{x_{\rm max}} k_sx^3\,dx = \dfrac{k_sx_{\rm max}^4}{4}$
This is equal to the change in the strain potential energy as a result of the extension. Consequently when the spring is extended by an amount x, its strain potential energy (relative to its unextended state x = 0) is
$E_{\rm strain} = \dfrac{k_sx_{\rm max}^4}{4}$
(Because some of the work done by the applied force might be dissipated, it is generally safer to calculate the work done by the conservative restoring force and then equate this with minus the change in strain potential energy. However in this case we are ignoring such a possibility.)
If we let the gravitational potential energy of the block be zero when the block is at its lowest point (i.e. when xlow = 0.30 m) then at any extension x
Egrav = mg (xlow − x)
And if we write the translational kinetic energy of the block at any point as
Etran = ½ mυx2
where υx = 0 when x = xlow, then we can use the principle of conservation of mechanical energy (Estrain + Egrav+ Etran = constant) at x = xlow = 0.30 m and at x = xeq = 0.10 m to write
$\dfrac{k_sx_{\rm low}^4}{4} + 0 + 0 + \dfrac{k_sx_{\rm eq}^4}{4} + mg(x_{\rm low} - x_{\rm eq}) + \dfrac12m\upsilon^2$
where υ is the speed of the block as it passes through its equilibrium position. Apart from υ, the only quantity in this equation without a known numerical value is ks, and we can determine its value from the existence of an equilibrium position at xeq = 0.10 m, which implies
mg = ksxeq3 so ks = mg/xeq3
It follows that
$\left(\dfrac{mg}{x_{\rm eq}^3}\right)\dfrac{x_{\rm low}^4-x_{\rm eq}^4}{4} - mg(x_{\rm low}-x_{\rm eq}) = \dfrac12m\upsilon^2$
i.e.$\upsilon^2 = \rm 9.81\left[\left(\dfrac{0.00810-0.00010}{0.002}\right)-0.400\right]\,m^2\,s^{-2} = 35.3\,m^2\,s^{-2}$
So,υ = 5.94 m s−1
Comment You may have chosen a different origin for your zero of gravitational energy, in which case your working will appear different, but it should produce the same result.
1.3 Ready to study?
Study comment To begin the study of this module you will need to be familiar with the following terms: acceleration, Cartesian coordinate system, components_of_a_vectorcomponent (of a vector), displacement, force, friction, gravitygravitation, magnitude_of_a_vector_or_vector_quantitymagnitude (of a vector), mass, Newton’s laws of motion, scalar, speed, uniform_acceleration_equationsuniform (or constant) acceleration equations, vector, velocity and weight. Also you will need to be familiar with the use of trigonometric functions, the idea of a derivative (e.g. dy/dx) and its graphical interpretation as the gradient of a suitable (y against x) graph. (However, it is not assumed that you are familiar with the mathematical techniques of differentiation.) If you are uncertain about any of these terms then you can review them now by reference to the Glossary which will also indicate where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
A stone is allowed to fall from rest from the top of a tall tower. If the speed of the stone is 31 m s−1 just before it hits the ground, calculate the height of the tower. Determine also the time taken for the stone’s fall. State any assumption made in solving this problem. (Take g = 9.81 m s−2)
Answer R1
Using the uniform acceleration equations, with the x–axis directed vertically downwards:
υx2 = ux2 + 2axsx
where υx = 31 m s−1, ux = 0, ax = g = 9.81 m s−2
sosx = (υx2 − ux2)/2ax = (3 ms−1)2/(2 × 9.8 ms−2) = 49.0 m
To determine the time taken for the fall, we use the equation:
υ2 = u2 + a2t i.e. t = (υ2 − u2)/a2
t = 31 m s−1/9.81 m s−2 = 3.16 s
In solving this problem it has been assumed that there is no resistance to motion caused by the air, and that the variation of g with height is insignificant over the distance involved.
Consult uniform acceleration equations in the Glossary for further information.
Question R2
A horizontal force of magnitude 16 N acts in the direction that is 60° south of west (i.e. the direction of the 7 from the centre of a circular clock face). What are the (scalar) components_of_a_vectorcomponents of the force in the south and west directions?
Answer R2
The south component of the force is (16 cos 30°) N = 13.9 N
The west component of the force is (16 cos 60°) N = 8 N
Consult components_of_a_vectorcomponent in the Glossary for further information.
Question R3
A person pushes a 10 kg box from rest along a rough floor with a constant, horizontal force of magnitude of 5.0 N, causing the box to cover a distance of 6.4 m in 8.0 s. Determine the magnitude and direction of the frictional force acting on the box. (You may find it helpful to introduce an x–axis pointing in the direction of the displacement.)
Answer R3
The constant force on the box will cause a constant acceleration. The value of the acceleration can be determined from the uniform acceleration equation:
sx = uxt + ½ axt2
If we substitute the following values sx = 6.4 m, ux = 0, and t = 8.0 s, we find
$a_x = \dfrac{2(s_x-u_xt)}{t^2} = \rm \dfrac{2\times6.4\,m}{64\,s^2} = 0.2\,m\,s^{-2}$
If the applied force is represented by Fx and the frictional force by fx, and applying Newton’s second law of motion, we can write:
max = Fx + fx i.e. fx = max− Fx
sofx = (10 × 0.2) N − 5.0 N = −3.0 N
This is a force of magnitude 3 N. The minus sign indicates that the direction of the frictional force opposes that of the motion.
Consult Newton’s second law of motion and uniform acceleration equations in the Glossary for further information.
2 Forces, work and kinetic energy
In everyday language we use the word work to refer to any activity that requires muscular exertion or mental effort. You know from everyday experience that when you lift an object, the heavier it is and the higher you lift it, the more the muscular exertion required. Also, if you push an object along a rough horizontal surface, the harder you push and the further you push, the more tired you get. This suggests that the ‘exertion’ depends on both the force applied and the displacement (i.e. change of position) which occurs. However, even when you just hold up a heavy object, when there is no displacement, your arms still become tired due to your exertion. The term ‘exertion’ here is imprecise.
In physics and engineering the terms work and work done are given a precise meaning, so that they can be quantified and measured in appropriate units. Although the terms work done and exertion are related, they are not equivalent nor are they interchangeable. One striking difference is that without a displacement there can be no work done in the precise technical sense. i In this section we will define work and work done.
We will also have to define energy carefully, since this too is a word which is used in an imprecise way in everyday language. Even at this stage it is useful to state that
Energy is the property of a body or system that gives it the capacity to do work.
As we investigate energy and try to formulate a clear definition of work we must remember that forces and displacements have directions as well as magnitudes and so are vector quantities, having three components in three–dimensional space. i We begin our discussion of work done with the simplest case – a constant resultant force acting in a fixed direction on a body, which undergoes a displacement along a straight line.
Study comment From now on the word force will be used as a shorthand to represent a resultant force or an unbalanced force.
2.1 Work done by a constant force acting on a body
A constant force acting along the line of a displacement
Imagine a body (e.g. a supermarket trolley) undergoing a displacement, and imagine yourself applying a constant force to that body along the line of the displacement. The force that you are applying may be responsible for the displacement (you might be pushing the trolley) but it doesn’t have to be (if somebody else was pushing the trolley your applied force might be intended to stop the trolley). In either case if we orientate the x–axis of a Cartesian coordinate system along the line of the displacement then we can specify the displacement by a single scalar_components_of_a_vectorcomponent sx, and the (constant) force by a single (constant) component Fx. If the displacement and the force are in the same direction (i.e. if they are parallel) then sx and Fx will have the same sign, if they are in opposite directions (i.e. antiparallel) they will have opposite signs. In either case, we define the work done by the force on the body as:
W = Fx sx(1)
From this definition we see that work is a scalar quantity since it is the product of two other scalars – the x–components of the force and the displacement. We also see that W will be positive if the force and the displacement are in the same direction, but it will be negative if the force and the displacement are in opposite directions. (Given the line along which the x–axis must lie, the choice of a direction for increasing values of x, i.e. the choice of the positive x–axis, is arbitrary. Thus, the signs of Fx and sx can both be changed by reversing that arbitrary choice, but the sign of the product Fx sx is independent of that particular choice.)
From Equation 1, the unit of work is the unit of force multiplied by the unit of displacement. In the SI system, the unit of work is thus the newton metre (N m). This unit is so important that it merits a special name – it is called the joule (J) in honour of the British physicist James Prescott Joule (1818–1889). Thus 1 J = 1 N m.
A constant force acting at an angle to the line of a displacement
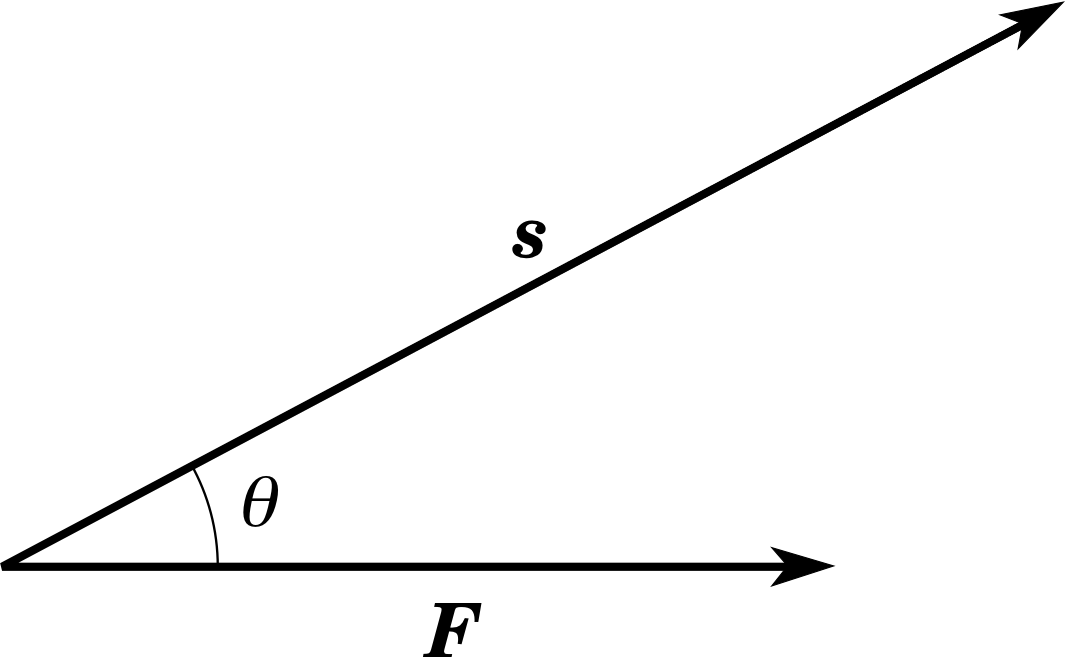
Figure 1 A body undergoes a displacement s while acted upon by a constant force F. If the angle between F and s is θ, then the work done is Fs cos θ.
We can extend our definition of work done to the case of a force acting at an angle to the direction of the displacement. In Figure 1 the force F acts at an angle θ to the displacement s of a body. In this case it is convenient to introduce a two–dimensional Cartesian coordinate system, in the same plane as F and s, so that we can express the force and the displacement in terms of their components; F = (Fx, Fy) and s = (sx, sy). Although it is not essential, we can further simplify matters by choosing to make the x–axis of the coordinate system parallel to the displacement, so that sy = 0 and sx = s, the magnitude of s. Using this two–dimensional coordinate system, a natural extension of Equation 1 is to define the work done by the force as the (scalar) sum of the work done by each of its components.
That is W = Fx sx + Fy sy(2)
Since sy = 0 in this case, and Fx = F cos θ we then have:
W = Fx sx = sx F cos θ
Moreover, because sx = s in this case we can write
W = Fs cos θ(3)

Figure 2 The product, Fs cos θ, of the magnitudes of two vectors and the cosine of the included angle may be looked upon as either, (a) the magnitude F multiplied by the component of s in the F direction (i.e. s cos θ) or (b) the magnitude s multiplied by the component of F in the s direction (i.e. F cos θ).
Now, although we have used a particular coordinate system to deduce Equation 3 the result that it expresses is actually independent of the coordinate system (it makes no reference to our arbitrarily chosen x–axis) and is true in general. So, no matter which way the x–axis is defined in the plane of F and s, we will always find that Equations 2 and 3 provide equally valid ways of calculating the work done by F over the displacement s.
Equation 3 is of particular significance since it shows that the work done by F can be thought of equally well in either of two ways:
- as the product of the magnitude of the displacement s and the component of F along s (as we have just done); or
- as the product of the magnitude of the force F and the component of the displacement vector s along F.
These two views are shown in Figure 2. No matter which view we take the work W is entirely determined by the magnitudes of the two vectors and the angle between them; more specifically
The work done by a constant force F acting over a displacement s is the product of the magnitudes of these two vectors and the cosine of the angle θ between them, i.e. W = Fs cos θ.
In Equation 3 the magnitudes F and s are always positive, but W may be positive or negative according to the value of the angle θ. We may distinguish several possibilities.
- 1
-
If θ = 0° in Equation 3, then cos θ = 1 and W is equal to the positive quantity Fs, as we would also have expected from Equation 1.
W = Fx sx(Eqn 1)
- 2
-
If θ lies between 0° and 90°, then the work done by F is still positive because the force has a positive component in the direction of the displacement.
- 3
-
If θ = 90°, then cos θ = 0 and the work done by F is zero. In this case the force has no component along the line of the displacement. (Or if you prefer, its component in that direction is 0).
- 4
-
If θ lies between 90° and 180°, then the work done by F is negative because it has a negative component in the direction of the displacement.
- 5
-
If θ = 180°, then cos θ = −1 and W is equal to the negative quantity −Fs, another result we might have anticipated from Equation 1.
This last case (W = −Fs) often arises when dealing with the frictional force that acts on a body as it slides across a surface. The frictional force opposes the relative motion of the body and the surface, and tends to reduce the speed of the sliding body. Thus, when a sliding motion causes a body to be displaced, the frictional force that opposes the motion will point in the opposite direction to the displacement (i.e. with θ = 180°) and the work done on the sliding body by that frictional force will be negative.
Question T1
How should you reword the following statement to make its precise meaning more obvious? ‘Five joules of work were done when I lifted a book from the floor to the table.’
Answer T1
The statement doesn’t tell us which force did the work on which body. A better statement would be: ‘Five joules of work were done on the book by the upward force I exerted when lifting the book from the floor to the table.’ You should always say which force is doing the work, and on which body the work is done.
Question T2
We usually think of frictional forces as opposing motion and thereby doing negative work on a body. However, in reality frictional forces oppose relative motion and may do positive or negative work. Describe one common situation in which a frictional force does positive work on a body. [Hint: Think of a situation in which a frictional force is used to make something move.]
Answer T2
If you put a book on a smooth table top and then drag your finger along the top of the book, the book will move in the same direction as your finger. The movement is a result of the frictional forces between your finger and the book which tend to reduce the relative velocity of your finger and the book. The frictional force on the book (due to your finger) acts in the same direction as any displacement that you cause and thereby does positive work on the book. (There is an equal and opposite force on your finger that does negative work on your finger, and there will be another frictional force on the underside of the book (due to frictional forces between the book and the table) which does negative work on the book.)
2.2 Vector treatment of work done by a constant force: the scalar product
In Subsection 2.1, working in two dimensions, we expressed a scalar quantity, work, as a ‘product’ of two vector quantities (force and displacement). The ‘product’ was a true scalar since it was actually defined as the product of the magnitudes of the two vectors and the cosine of the angle between them, all of which are scalar quantities. We can now extend this idea to the three dimensions of the real world as follows:
Suppose F = (Fx, Fy, Fz) and s = (sx, sy, sz)
then, if F is a constant force that is applied to a body that undergoes a displacement s, the work done by the force on the body may be expressed in terms of the magnitudes of the two vectors and the angle between them as:
W = Fs cos θ (Eqn3) i
Alternatively, the work done may be expressed in terms of the components of the vectors as:
W = Fxsx + Fysy + Fzsz(4)
It can be shown that these two expressions (Equations 3 and 4) are entirely equivalent, and it is conventional to represent them by F ⋅ s, so we can write
W = Fxsx + Fysy + Fzsz = Fs cos θ = F ⋅ s(5)
The term F ⋅ s in Equation 5 is an example of a mathematical entity called the scalar product (or the dot product) of two vectors. In general, the scalar product of any two vectors a = (ax, ay, az) and b = (bx, by, bz) is defined by:
a ⋅ b = axbx + ayby + azbz = ab cos θ(6) i
where a and b are the magnitudes of a and b, respectively, and θ is the angle between them.
The scalar product of two vectors has many uses in physics. It arises whenever two vectors must be multiplied together to produce a scalar – hence its name. (The alternative name dot product reflects the fact that a bold dot between two vectors is used to indicate the scalar product, as in a ⋅ b.) The fact that the scalar product may be expressed in the form ab cos θ shows that its value is independent of the coordinate system we choose to use when specifying a and b in terms of their components. If we changed the coordinate system we would change the values of the six components, but the value of the scalar product a ⋅ b = axbx + ayby + azbz would remain unchanged. This makes good physical sense – we don’t expect the work done by a force F over a displacement s to depend on the coordinate system we choose to use when specifying F and s.
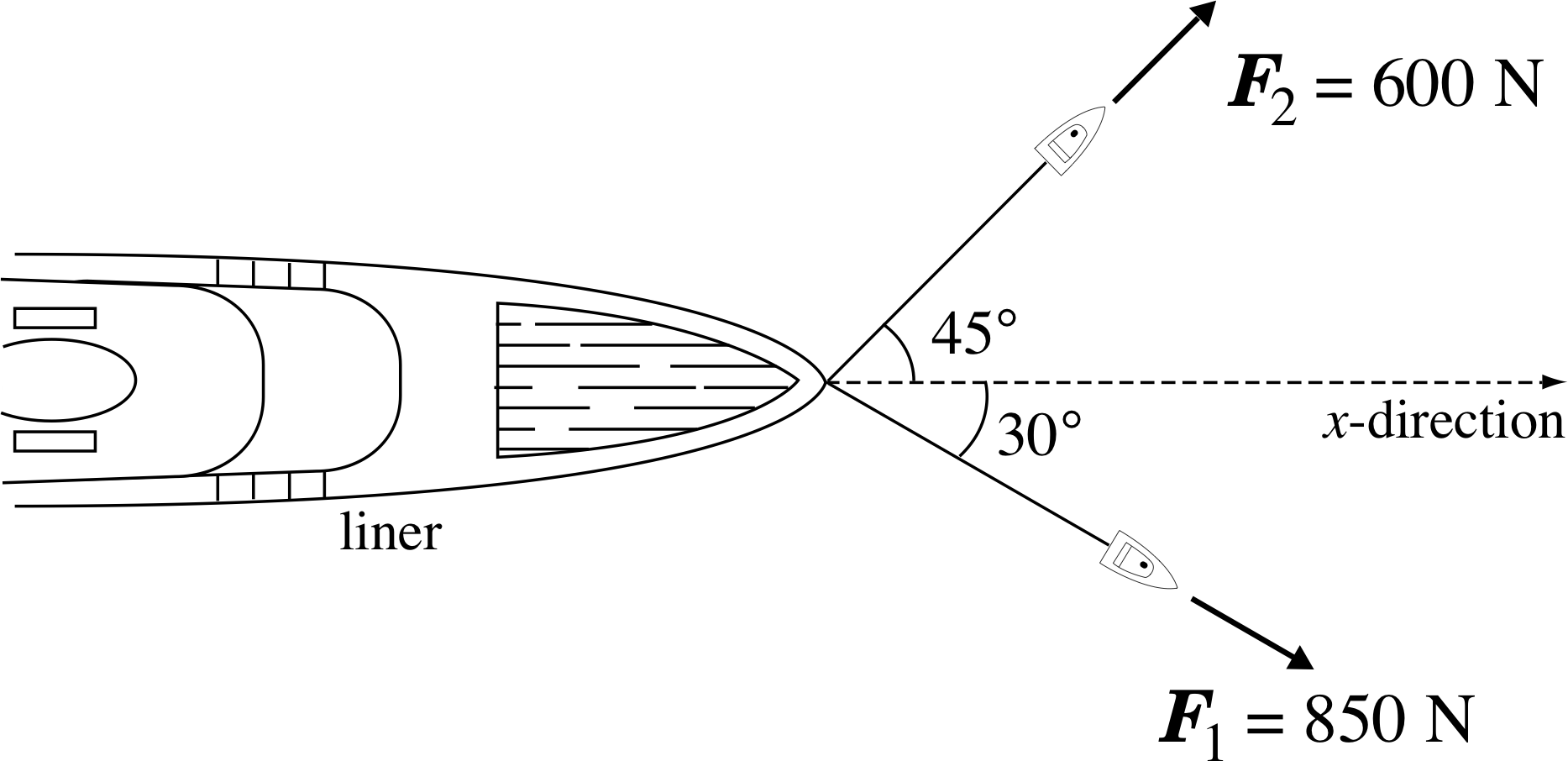
Figure 3 Top view of a liner pulled along by two forces.
✦ A liner is pulled into a harbour by two horizontal ropes attached to tugs as shown in Figure 3. How much work is done on the liner by each of the forces shown when the liner is moved 70 m in the x–direction?
✧ Using W = F ⋅ s for each of the forces:
W1 = F1s cos 30° = 850 N × 70 m × cos 30° = 5.2 ×104 J
W2 = F2s cos 45° = 600 N × 70 m × cos 45° = 3.0 ×104 J
✦ (a) If F = (2.0 N, 3.0 N, −1.0 N) and s = (70 m, 0 m, 0 m), find the work done when the constant force F acts over the displacement s.
(b) Evaluate the magnitudes of F and s and use your results, together with your answer to part (a), to determine the angle θ between F and s. (You may find it useful to draw a diagram showing the relative directions of F and s.)
✧ (a) W = F ⋅ s = 2.0 N × 70 m + 3.0 N × 0 m − 1.0 N × 0 m = 140 J
(b) $F=\sqrt{\smash[b]{F_x^2+F_y^2+F_z^2}} = \sqrt{\smash[b]{(2.0 N)^2+(3.0 N)^2+(−1.0 N)^2}} = \rm 3.74\,N$
and$s = \sqrt{\smash[b]{s_x^2+s_y^2+s_z^2}} = \rm 70\,m$
ButW = F ⋅ s = Fs cos θ
so140 J = 3.74 N × 70 m × cos θ
i.e.cos θ ≈ 140/262 ≈ 0.534 and so θ ≈ arccos 0.534 ≈ 57.7° i
2.3 Work done and the change in translational kinetic energy
In Subsection 2.1 we noted that the frictional force which tends to slow down a sliding body does negative work. In this subsection we use the uniform acceleration equations and Newton’s laws of motion to investigate how the speed of a body changes when forces act on it, with a view to finding a general relationship between the work done by the forces and the change in ‘motion’ of the body. As usual, we begin by considering the case of one–dimensional motion along the x–axis, and for the sake of simplicity we will suppose that the ‘body’ in question is actually a particle without any internal structure, so it can be characterized by its mass, position, speed and acceleration, but we don’t have to worry about the possibility that it might be spinning or wobbling.
When a single constant force Fx acts on a particle of mass m the acceleration it produces is given by Newton’s second law of motion as ax = Fx /m. If the initial velocity of the particle is ux and the force acts for a time t the final velocity of the particle υx is:
υx = ux + axt(7)
The displacement of the particle at time t (measured from its initial position) is denoted sx and is related to υx, ux and ax by:
υx2 = ux2 + 2axsx(8)
so$s_x = \dfrac{\upsilon_x^2-u_x^2}{2a_x} = \dfrac{m(\upsilon_x^2-u_x^2)}{2F_x}$
Multiplying both sides of this equation by Fx we see that the work W done on the particle by the constant force Fx acting over the displacement sx is given by:
$W = F_x s_x = \dfrac{m(\upsilon_x^2-u_x^2)}{2} = \dfrac12 m\upsilon_x^2-\dfrac12 u_x^2$(9a)
Equation 9a shows very clearly how the velocity component υx changes in response to the work done by the force, but we can rewrite it in a somewhat more memorable form. Because we are only considering one–dimensional motion at this stage, we can say ux2 = u2 and υx2 = υ2, where u and υ are the initial and final speeds, respectively. It is useful for many purposes to introduce a quantity called the translational kinetic energy of a particle which is defined by the relation
translational kinetic energy Etran = ½ mυ2(10)
where m is the mass of the particle and υ is its speed.
You have probably met the idea of kinetic energy before; it is usually described as ‘energy by virtue of motion’. However, you should note that in this discussion we are only interested in the translational kinetic energy that arises from the overall movement of the particle. Larger bodies might spin on an axis or vibrate internally, thereby acquiring rotational or vibrational kinetic energy, but by considering a structureless particle we have deliberately excluded these possibilities. i In what follows we will continue to use the symbol Etran but we will sometimes refer to it simply as the kinetic energy, leaving you to remember that we are only concerned with translational kinetic energy in this module.
We can now identify the quantity ½ mυ2 in Equation 9a
$W = F_x s_x = \dfrac{m(\upsilon_x^2-u_x^2)}{2} = \dfrac12 m\upsilon_x^2-\dfrac12 u_x^2$(Eqn 9a)
as the initial translational kinetic energy of the particle and ½ mυ2 as its final translational kinetic energy. It then follows that
W = final translational kinetic energy – initial translational kinetic energy
This relation (which we have only proved in one dimension, so far) makes no reference to any particular direction, and actually remains true in three dimensions.
It is often stated more formally as the work–energy theorem:
When a single resultant force does work on a particle, the translational kinetic energy of the particle changes by an amount which is equal to the total work done on the particle by that force. These changes can be positive or negative.
✦ What is the SI unit of kinetic energy? Two important aspects of kinetic energy are worth noting:
✧ From Equation 9a,
$W = F_xs_x = \dfrac12m(\upsilon_x^2-u_x^2) = \dfrac12m\upsilon_x^2 - \dfrac{1}{2}mu_x^2$
the unit of kinetic energy can be seen to be the same as the unit of work, i.e. the joule (J).
- 1
-
Kinetic energy is a scalar quantity, as is essential if we are to relate changes in kinetic energy to the scalar quantity of work done.
- 2
-
Unlike work done, kinetic energy can only be positive. In our one–dimensional discussion above, the velocity components ux and υx may be positive or negative but their squares, ux2 and υx2, must remain positive. This is consistent since it is the changes in kinetic energy which relate to work done, and these changes can be positive or negative.
It is straightforward to extend our one–dimensional discussion of work and kinetic energy to the three–dimensional case in which F = (Fx, Fy, Fz), s = (sx, sy, sz), u = (ux, uy, uz) and υ = (υx, υy, υz). The argument that led to Equation 9a can then be applied to each component separately. This again yields Equation 9a,
$W = F_x s_x = \dfrac{m(\upsilon_x^2-u_x^2)}{2} = \dfrac12 m\upsilon_x^2-\dfrac12 u_x^2$(Eqn 9a)
and, in addition, also leads to the analogous results
$\phantom{W~=} F_ y s_y = \dfrac{m(\upsilon_y^2-u_y^2)}{2} = \dfrac12 m\upsilon_y^2-\dfrac12 u_y^2$(9b)
and$\phantom{W~=} F_z s_z = \dfrac{m(\upsilon_z^2-u_z^2)}{2} = \dfrac12 m\upsilon_z^2-\dfrac12 u_z^2$(9c)
If we add together the three Equations 9a, 9b and 9c we obtain the three–dimensional result:
Fxsx + Fysy + Fzsz = ½ m (υx2 + υy2 + υz2) −½ m (ux2 + uy2 + uz2)(11)
Butux2 + uy2 + uz2 = u2 and υx2 + υy2 + υz2 = υ2
where u and υ are the initial and final speeds, respectively. The right–hand side of Equation 11,
Fxsx + Fysy + Fzsz = ½ m (υx2 + υy2 + υz2) − ½ m (ux2 + uy2 + uz2)(Eqn 11)
is the change in the kinetic energy, while the left–hand side is the work done on the particle by the force.
In vector notation this is given as:
W = F ⋅ s = ½ mυ2 − ½ mu2 = (Etran)f − (Etran)i = ∆Etran(12)
where the subscripts f and i stand for ‘final’ and ‘initial’, ∆Etran is the change in the kinetic energy and W is the work done on the particle by the single constant force F acting over the displacement s. Equation 12 confirms that the work–energy theorem is also valid in the three–dimensional case. Note that the kinetic energy of the particle increases if positive work is done on it whereas the kinetic energy decreases if negative work is done on it.
Question T3
Suppose that you apply a lifting force to a book of mass m so that it is raised to a height h above the ground. Suppose also that the book is stationary at the beginning and the end of the lifting process. Work has been done on the book by the lifting force yet the kinetic energy of the book has not changed; how is this reconciled with the work–energy theorem?
Answer T3
The work–energy theorem relates to the single (resultant) force that acts on a particle. However, the lifting force referred to in the question is not the only force that acts on the mass; there is also a downward force due to gravity – the weight of the book. Hence the work–energy theorem does not apply to the lifting force, but it does apply to the resultant force that acts on the book. The work done by the lifting force equals mgh, but the work done by the force of gravity is −mgh, so there is no work done on the book by the resultant force and therefore no change in the kinetic energy.
Comment There is a change in another quantity called potential energy (as will be discussed in Subsection 3.2).
Question T4
The brakes on a car of mass 1000 kg travelling at a speed of 15 m s−1 are suddenly applied so that the car skids to rest in a distance of 30 m. Use energy considerations to determine the magnitude of the total frictional force acting on the tyres, assuming it to be constant throughout the braking process. What is the car’s speed after the first 15 m of this skid?
Answer T4
The work done on a car, of mass m and initial velocity ux, by a frictional force fx, acting over a displacement sx, is equal to the change in the translational kinetic energy:
i.e fxsx = −fs = 0 − ½ mux2
where f is the magnitude of the frictional force, s is the magnitude of the displacement, and we have used the fact that the force and the displacement are oppositely directed. It follows that:
f = 1000 kg × (15 m s−1)2/(2 × 30 m) = 3750 N
When the car has skidded half the total stopping distance, half of the original kinetic energy remains. If the velocity at this point is υx then:
$\frac12m\upsilon_x^2 = \frac14mu_x^2$
so$\upsilon_x = \dfrac{u_x}{\sqrt{2\os}} = \rm \dfrac{15\,m\,s^{-1}}{\sqrt{2\os}} = 10.6\,m\,s^{-1}$
2.4 Work done in compressing or stretching a spring
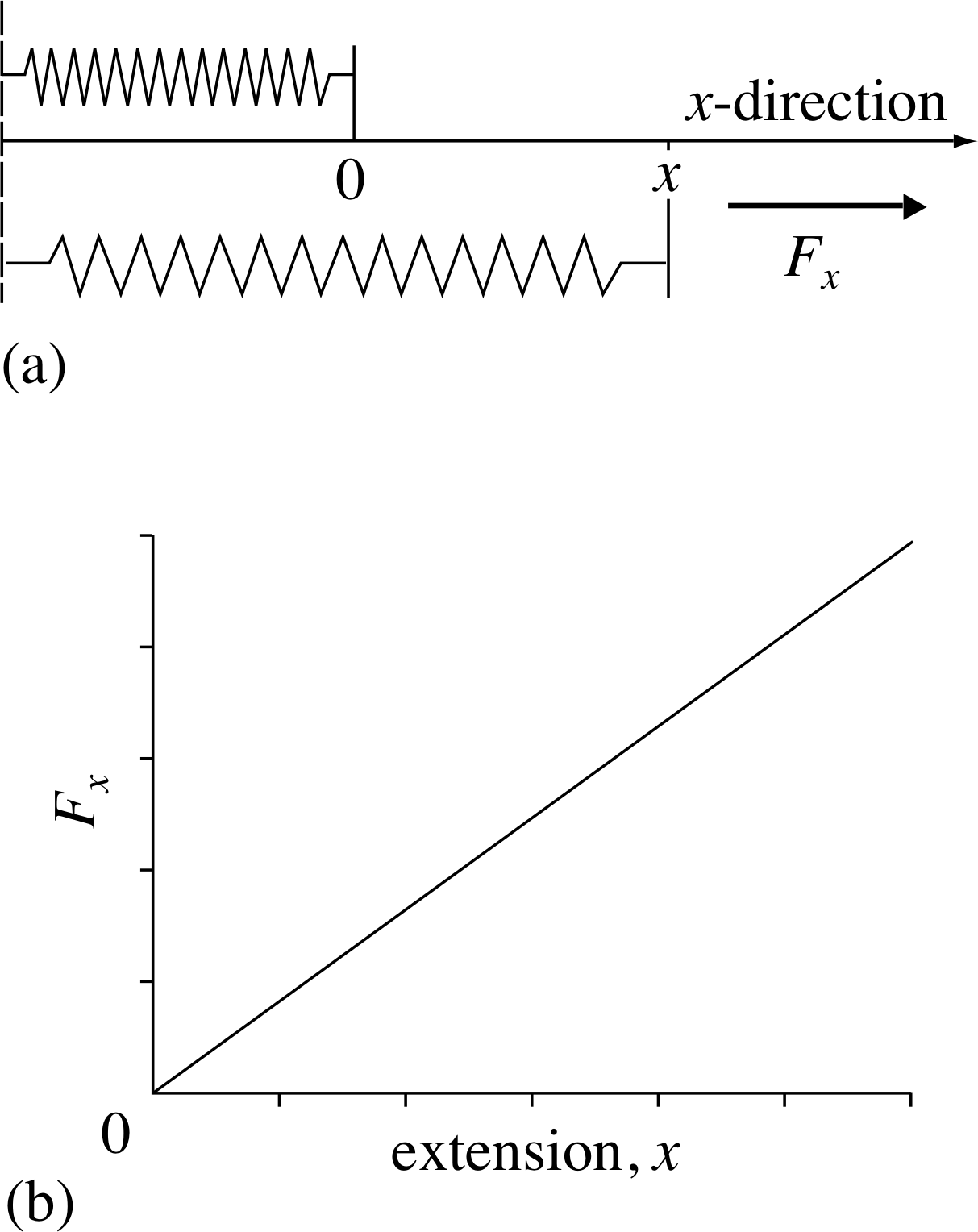
Figure 4 (a) The applied force Fx required to stretch or compress a spring with one fixed end. The extension x may be positive (when the spring is stretched) or negative (when compressed) and represents the displacement of the free (mobile) end of the spring from its unstretched position. (b) Variation of the applied force Fx with the extension x for a spring that obeys Hooke’s law (the spring constant ks determines the gradient of the graph).
Until now we have considered only work done by a constant force which is independent of the displacement. We will now consider cases where the force depends on the displacement. As usual, we will start by considering a one–dimensional example.
What happens when you stretch or compress a spring or any other elastic i body which is fixed at one end? Generally speaking, the more the spring or body is stretched or compressed, the greater the force you have to apply to stretch or compress it further. Thus, the force you must apply when stretching or compressing such a body varies in strength throughout the process. Nonetheless, whether you are stretching or compressing the body the applied force is generally in the direction of the displacement it causes and therefore does positive work in the process. Finding an expression for the work done by such a force is the main aim of this subsection.
Clearly, that expression must take into account the particular way in which the force varies as the body is distorted, and this may be quite complicated so we will start by considering the work done in stretching or compressing a simple spring of the kind shown in Figure 4a.
As you can see from Figure 4, the spring is extended along the x–axis of a coordinate system, and we have chosen the origin (x = 0) in such a way that it marks the location of the free (mobile) end of the spring when it is in its unstretched state. By setting–up the coordinate system in this way we ensure that the position coordinate x of the mobile end of the spring is always equal to the displacement sx of the mobile end from its unextended position, so we can write sx = x in this case. We can describe this in another way by saying that the position coordinate x of the mobile end of the spring represents the extension of the spring; this extension will be positive when the spring is stretched, and negative when it is compressed.
We will also assume that the particular spring we are considering obeys Hooke’s law, which requires that the applied force which stretches or compresses a spring is directly proportional to the extension it produces. Consequently, a graph of the applied force Fx against the extension x will be linear and will pass through the origin, as shown in Figure 4b. Algebraically we can represent Hooke’s law by:
Fx = ks x
where ksis a constant that characterizes the spring, called the spring constant. The mobile end of the spring is also subject to a restoring force that arises from tension within the spring and acts in the opposite direction to the applied force Fx. When the spring is maintained at some particular extension x the restoring force must exactly balance the applied force, so (Frest)x = −Fx and it is therefore not unusual to see Hooke’s expressed by an equation of the form (Frest)x = −ksx.
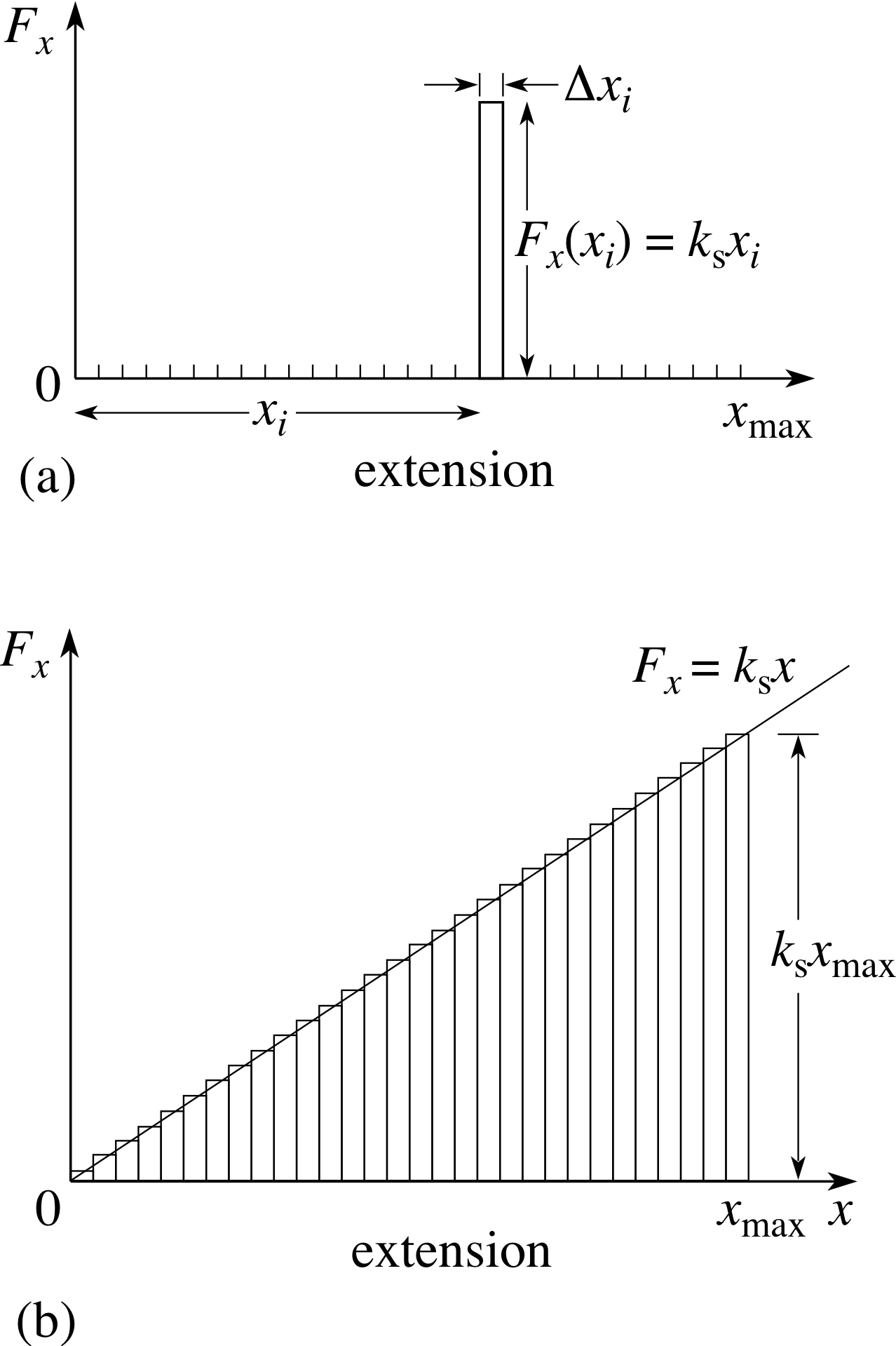
Figure 5 (a) The work done on a spring by a force Fx in producing a small extension ∆xi. (b) The total work done on the spring to produce an extension xmax, viewed as the sum of the work done in a sequence of small extensions.
Since the applied force depends on the extension x, it makes good sense to say that Fx is a function of x and to denote it by Fx(x). Thus we may also write Hooke’s law in the form
Fx(x) = ksx i
To calculate the work done on the spring by an applied force Fx(x) when the mobile end of the spring is displaced from its unextended position x = 0 to some particular point x = xmax we must take into account the changing value of Fx(x) throughout the displacement. This can be done by supposing that the total work done is the result of adding together the work done in a succession of n small extensions
each of which involves displacing the mobile end of the spring by such a tiny amount that the applied force is almost constant throughout each such small extension (Figure 5).
The work done in any one of those small extensions, such as the ith one, in which the mobile end of the spring is displaced from xi to xi + ∆xi and the force is approximately Fx(xi) throughout, will then be given approximately by:
∆Wi ≈ Fx(xi) ∆xi(13a)
This small amount of work is represented in Figure 5a by the area of the small rectangle of width ∆xi and height Fx(xi) = ksxi.
The total work W done over the full displacement from x = 0 to x = xmax will then be approximately equal to the total area of all the small rectangles in Figure 5b, and may be represented algebraically by
$\displaystyle W = F_x(x_1)\Delta x_1 + F_x(x_2)\Delta x_2 + \cdots + F_x(x_n)\Delta x_n = \sum_{i=1}^n F_x(x_i)\Delta x_i$(13b) i
The approximation in Equation 13b (or Figure 5b) will become increasingly accurate as the size of the displacements ∆xi are reduced, since the assumed constancy of F (xi) throughout each small displacement will then be more justified. We can indicate this by saying that the sum in Equation 13b is equal to the work done in stretching the spring in the limit as ∆x tends to zero, and writing
$\displaystyle W = \lim_{\Delta x\rightarrow 0}\sum_{i=0}^n F_x(x_i)\Delta x_i$(13c) i
Now, in terms of Figure 5b, if we allow the extension increments ∆xi to become smaller and smaller then the total area of all the small rectangles will approach the triangular area under the force–extension graph (the line Fx = ksx) between x = 0 and x = xmax. Since that triangle has a base of length xmaxand a height Fx(xmax) = ksxmax, its area is
½ Fx(xmax) × xmax = ½ ksx2max
Thus, the work done on a spring that obeys Hooke’s law by an applied force in extending the spring by an amount xmaxfrom its unextended position is:
W = ½ ksx2max(14)
Note that since xmax appears as a squared term, the work done depends on the magnitude but not on the sign of xmax and so it is the same whether the spring is stretched or compressed. As expected, the work done on the spring is always positive and Equation 14 implies that the only condition in which W = 0 is when x = 0 and the spring is not distorted.
✦ What is the work done by the tension in the spring (a restoring force) if an applied force increases the extension from 0 to some positive value xmax?
✧ The work done by the restoring force is the negative quantity $\frac{1}{2}kx_{\rm max}^2$, since the tension is equal in magnitude but opposite in direction to the applied force for any extension value.
Question T5
How much work must be done by an applied force to increase the extension of a spring that obeys Hooke’s law (with ks = 200 N m−1) from 15 cm to 20 cm? How does this compare with the work done in increasing the extension from 20 cm to 25 cm?

Figure 4 (a) The applied force Fx required to stretch or compress a spring with one fixed end. The extension x may be positive (when the spring is stretched) or negative (when compressed) and represents the displacement of the free (mobile) end of the spring from its unstretched position. (b) Variation of the applied force Fx with the extension x for a spring that obeys Hooke’s law (the spring constant ks determines the gradient of the graph).
Answer T5
Arranging coordinates as in Figure 4a, we can use Equation 14,
W = ½ kx2(Eqn 14)
to calculate the work W (x) that must be done to increase the extension from 0 to x. It follows that
W (15 cm) = [0.5 × 200 × (0.15)2] J = 2.25 J
W (20 cm) = [0.5 × 200 × (0.20)2] J = 4.0 J
W (25 cm) = [0.5 × 200 × (0.25)2] J = 6.25 J
It follows that the work done in increasing the extension from 15 cm to 20 cm is W (20 cm) − W (15 cm) = 1.75 J, while the work done in increasing the extension from 20 cm to 25 cm is W (25 cm) − W (20 cm) = 2.25 J.
Although Equation 14,
W = ½ ksx2max(Eqn 14)
only applies to forces described by the equation Fx(x) = ksx, the method that was used to derive it is quite general and may be applied in other situations. So, provided we know the specific function Fx(x) that relates the applied force to the extension x, we can always say that:
$\displaystyle W = \lim_{\Delta x\rightarrow 0} \sum_{i=1}^n F_x(x_i)\Delta x_i$(Eqn 13c)
where the n small extensions ∆xi cover the full displacement from x = 0 to x = xmax. (Of course, as the ∆xi become smaller n must become larger.)
Now this kind of limit of a sum over a specified range is very common in physics and mathematics and is generally referred to as a definite integral. So important are definite integrals that there is a special notation for writing them down that avoids all the clumsiness of Equation 13c. Using this standard notation Equation 13c can be rewritten as:
$\displaystyle W = \int_0^{x_{\rm max}} F_x(x)dx$(15)
As you can see, a large distorted ‘S’ (called the integral sign), sandwiched between the upper and lower ends of the range (called the upper and lower limits of integration), is used to indicate the process of taking the limit of a sum. The variable x (the integration variable) that changes continuously across the range is indicated by writing an integration element dx on the right of the integral, and the quantity that depends on the integration variable (the integrand) is written in the centre. It is important to note that whatever the exact form of the integrand Fx(x), you can still interpret Equation 15 as indicating that the work done is given by the area under the force–extension graph between x = 0 and x = xmax. i
In the particular case that Fx(x) = ksx, we already know that
$\displaystyle W = \int_0^{x_{\rm max}} F_x(x)\,dx = \int_0^{x_{\rm max}} k_s x\,dx = \dfrac12 k_sx_{\rm max}^2$
but if the applied force had been related to x by some other formula, such as Fx(x) = ksx3, then we could have written
$\displaystyle W = \int_0^{x_{\rm max}} F_x(x)\,dx = \int_0^{x_{\rm max}} k_s x^3\,dx$
which can be interpreted graphically as meaning that W is equal to the area under the graph of Fx(x) = ksx3 between x = 0 and x = xmax. If you drew that graph and measured that area you would find that $W = \frac14k_sx_{\rm max}^4$ though it would require quite a lot of drawing and measuring to confirm this. Fortunately, there is an easier way. Given the particular expression for Fx(x) that applies to any particular problem there are a number of standard techniques that will often enable you to evaluate the corresponding definite integral algebraically, without drawing any graphs. These techniques are a major part of the subject of integration – the analysis and evaluation of integrals – they will not be used in this module, but many of them are developed in detail in the maths strand of FLAP. Their existence makes it relatively easy to apply Equation 15 to a vast range of problems.
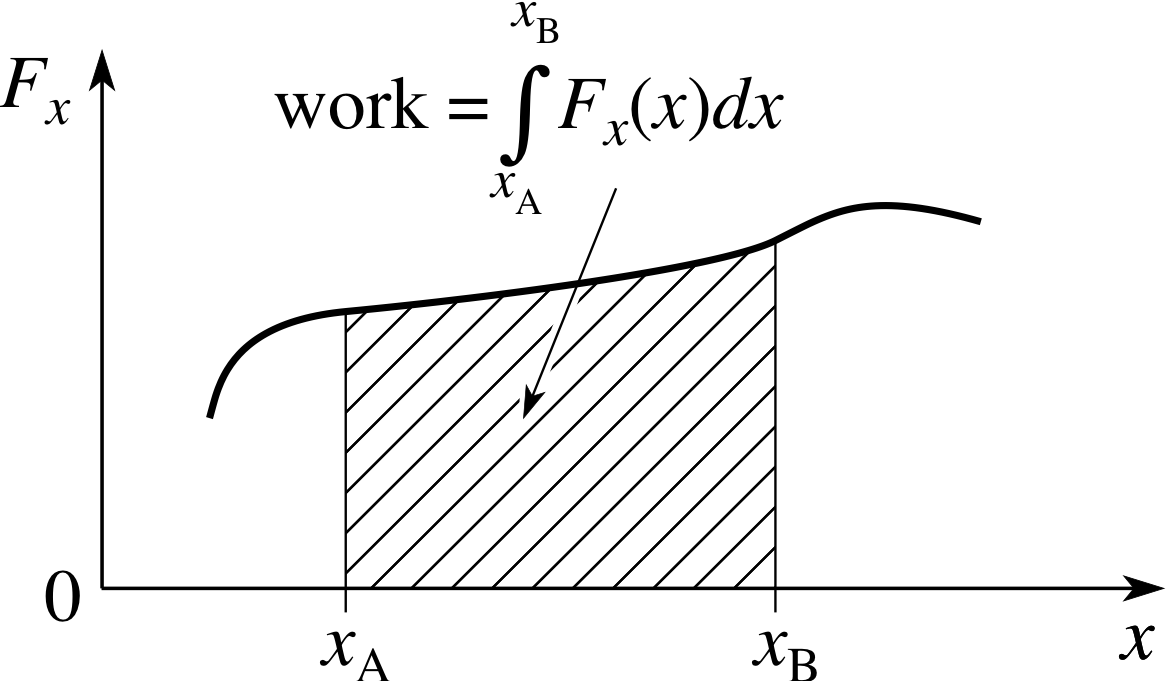
Figure 6 The work done by an arbitrary one–dimensional force Fx acting over an arbitrary displacement in the line of the force.
Before finishing this subsection and moving on to three dimensions it is worth noting a simple generalization of Equation that is often of great value. Suppose you want to calculate the work done by an applied force in changing the extension of a spring from some initial value x = xA to some final value x = xB. This is the kind of problem that was considered in Question T5 for a spring that obeys Hooke’s law. But how do we deal with a spring that doesn’t necessarily obey Hooke’s law? Let us suppose the relevant force–extension graph for this particular spring is the one shown in Figure 6.
Following the usual procedure of dividing the full displacement into small steps, adding together the work done in each step and then considering the limit of the sum as the individual steps become vanishingly small leads to the conclusion that the required amount of work is represented by the area under the force–extension graph between x = xA and x = xB.
We can use the definite integral notation to write this as
$\displaystyle W = \int_{x_{\rm A}}^{x_{\rm B}} F_x(x)\,dx $(16)
Although we have used the example of an extended spring to arrive at this result, the only essential ingredients from the mathematical point of view are the applied force Fx(x) and the displacement (from x = xA to x = xB) over which it acts. We may therefore summarize our final result by saying
The total work done by a force acting in the direction of a displacement over the displacement is given by the area under the force–displacement graph between the limits of the displacement. This may be found graphically or by integration.
2.5 Work done by a force which varies in magnitude and direction
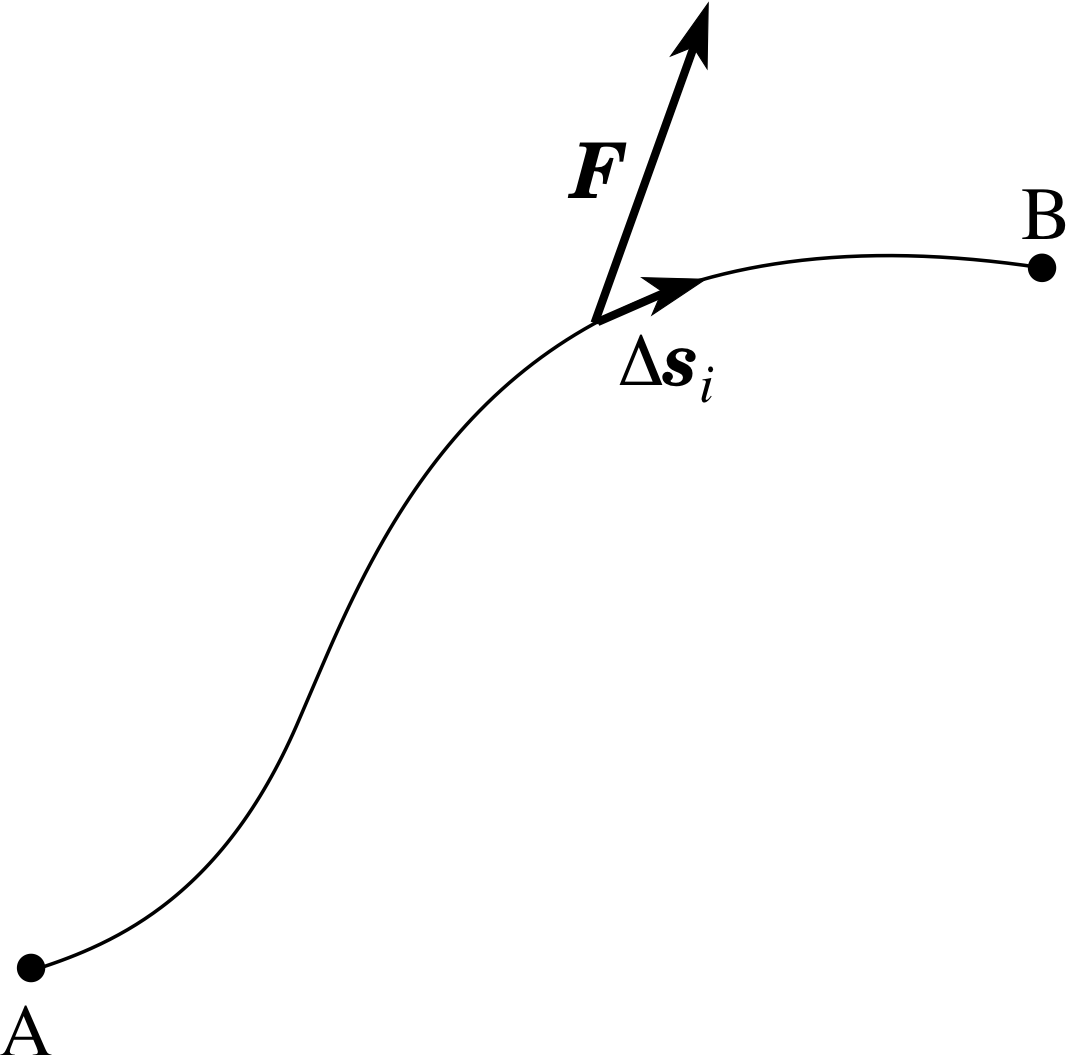
Figure 7 An object moves along a curved path from A to B. The path is divided into small displacements ∆si. The work done on the object by the (varying) force F over the displacement ∆si is approximately ∆Wi ≈ F ⋅ ∆si.
In the previous example the magnitude of the force was allowed to vary but not its direction. In the most general case both the magnitude and the direction of the force vary and the body moves along a curved path through space. (As an example you might like to think of a roller–coaster acted upon by a resultant force arising from gravity, friction, air resistance, etc.) Suppose the body moves from point A to point B along a curve as shown in Figure 7. As before, we can imagine dividing the path into n very small displacements, but in this three–dimensional case each of those small displacements must be a vector, so we will denote the ith displacement by ∆si, where ∆si = (∆xi, ∆yi, ∆zi). We suppose that each such displacement is sufficiently small that the force is virtually constant over it. The work done by F over ∆si is then approximately given by the scalar product:
∆Wi ≈ F ⋅ ∆si = Fx ∆xi + Fy ∆yi + Fz ∆zi i
The total work done by F as the object moves from A to B is obtained by summing the work done over all the displacements and taking the limit as the ∆si approach zero (i.e. as ∆xi, ∆yi, and ∆zi approach zero i ):
$\displaystyle W = \lim_{\Delta \boldsymbol{s}\rightarrow 0} \sum_{i=1}^n \boldsymbol{F} \cdot \Delta \boldsymbol{s}$
As in the last subsection, we can rewrite this limit of a sum as a definite integral. Thus we can say that the work done by a force F over the given path from A to B is
$\displaystyle W = \int_{\rm A}^{\rm B} \boldsymbol{F} \cdot d\boldsymbol{s}$(17)
Such an integral is called a line integral. To evaluate it we would need to know the exact shape of the path so that we could determine the value of F at each point along the path. Performing such an evaluation is beyond the scope of this module.
3 Conservative forces, potential energy and energy conservation
In Section 2 the concept of kinetic energy was introduced as the energy possessed by a particle due to its motion. In this section the concept of potential energy will be introduced as the energy possessed by a particle or a body due to its position or its internal state. When a single resultant force acts on a particle the work done by that force changes the kinetic energy of the particle, but when two or more forces act on a particle the work done by any of those forces may change the body’s potential energy as well as or instead of its kinetic energy. The discussion of energy changes contained in this subsection will lead us to introduce the principle of conservation of mechanical energy and the more general principle of conservation of energy.
3.1 Conservative and non–conservative forces
Despite its title, this subsection has nothing to do with politics! Forces can be classified as either conservative or non-conservative, according to how they behave when doing work on a particle – basically, on whether that work is fully recoverable or not.
To understand what a conservative force is, consider the process of lifting a stone of mass m slowly and vertically from the ground to a given height h, and then lowering it slowly and vertically back to the ground again. i Of course, forces must be applied to cause this motion but for the moment we will ignore all forces except for the constant gravitational force i (i.e. the weight of the stone) which is directed downwards and has magnitude mg throughout the motion. i From Equation 3,
W = Fs cos θ(Eqn 3)
this force is seen to do negative work, −mgh, during the lifting, (since the angle between the gravitational force and displacement is 180°) and positive work, +mgh, during the lowering. Thus the total work done by gravity over the complete (closed) path is zero. We will now show that this conclusion is valid for any closed path (not necessarily vertically up and down); it is this property which makes the gravitational force a conservative force.
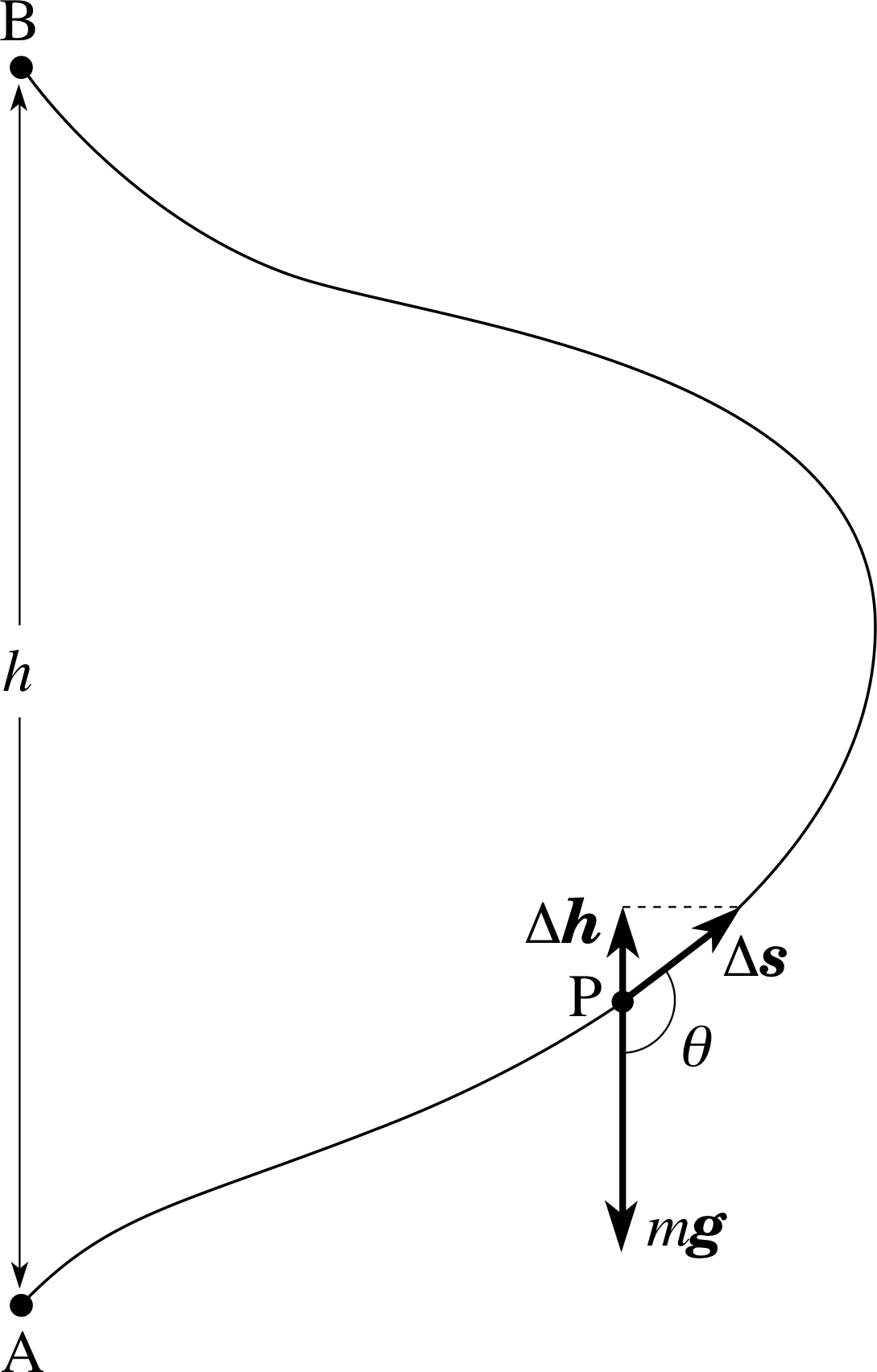
Figure 8 A stone is lifted from A to B via an arbitrary path.
Figure 8 shows a stone of mass m being lifted from point A to point B, through a height h, via an arbitrary path that passes through a point P. If the stone undergoes a small displacement ∆s from P then the work done by the gravitational force over that displacement will be
∆W = Fgrav ⋅ ∆s i
i.e.∆W = mg∆s cos θ
where ∆s is the magnitude of ∆s. From Figure 8 it can be seen that
∆s cos θ = −∆h
so∆W = −mg∆h(18)
This tells us that the work done over the displacement ∆s depends only on the height change ∆h along ∆s and not directly on ∆s itself or on θ. It is then clear that the work done by gravity between A and B, which is just a succession of such small changes, also depends only on the total height difference and not on the details of the path chosen.
We can indicate this by writing:
$\displaystyle W_{\rm AB} = \sum_{\rm A}^{\rm B} \Delta W = -\sum_{\rm A}^{\rm B} mg\Delta h = -mg \sum_{\rm A}^{\rm B}\Delta h = -mgh$(19) i
or, as an integral:
$\displaystyle W_{\rm AB} = \int_{\rm A}^{\rm B} dW = -\int_{\rm A}^{\rm B} mg dh = -mg \int_{\rm A}^{\rm B} dh = -mgh$(20)
Thus, the total work done by the gravitational force over any path from A to B is simply WAB = −mgh. Similarly, the return journey from B to A by any path has WBA = +mgh, so the round trip by any path is completed with zero net work done by gravity.
In general, conservative and non-conservative forces are defined as follows:
A force acting on a particle is said to be conservative_forceconservative if the work that it does when the particle moves around a closed path is zero, irrespective of the choice of closed path. Forces which do not satisfy this condition (i.e. those for which there is a closed path around which the work done is not zero) are said to be non_conservative_forcenon–conservative. i
An equivalent definition of a conservative force that may be shown to be a direct consequence of the first is the following:
A force acting on a particle is said to be conservative if the work that it does when the particle moves from point A to point B is independent of the path that the particle follows from A to B. Forces which do not satisfy this condition (i.e. those for which the work done between A and B is path dependent) are said to be non-conservative. i
Question T6
A conservative force F = (Fx, Fy, Fz) = (2x2 N, 3y N, 5 N) acts on a particle, which is initially at rest at the origin (0, 0, 0). While this force continues to act the particle is moved to the point (x, y, z) = (3 m, 1 m, −2 m). Calculate the work done by the force during the movement. (If you are unfamiliar with the techniques of integration you will find it useful to know that the area under a graph of the function Fx = 2x2 N between x = 0 and x = 3 m is 18 N m = 18 J. Note that the given force is not the cause of the motion in this case.)
Answer T6
Using Equation 17,
$\displaystyle W = \int_{\rm A}^{\rm B} \boldsymbol{F} \cdot d\boldsymbol{s}$(Eqn 17)
the work done on the particle is:
$\displaystyle W = \int_0^{3\,{\rm m}} (2x^2\,{\rm N})\,dx + \int_0^{1\,{\rm m}} (3y\,{\rm N})\,dy +\int_0^{-2\,{\rm m}} (5\,{\rm N}) dz$
As the question indicates, the first of the three definite integrals is equal to 18 J. The second represents the triangular area under the straight line graph of Fy = 3y N between y = 0 and y = 1 m, this is a triangle of height Fy = 3 N and base 1 m, so its area is 1.5 N m = 1.5 J. The third integral represents the work done by a constant force Fz = 5 N over an oppositely directed displacement ∆z = −2 m, that is −10 N m = −10 J. Thus the total work done is W = 9.5 J.
If you are familiar with the techniques of integration you can confirm these results by noting that
$W = \rm \left[\dfrac{2x^3\,N}{3}\right]_0^{3\,m} + \left[\dfrac{3y^2\,N}{2}\right]_0^{1\,m} + \left[5z\, N\right]_0^{-2\,m} = \left(18+\dfrac32-10\right)\,J = 9.5\,J$
We have already seen that the gravitational force on a body is conservative, but it is important not to make the mistake of thinking that every force is conservative. To find an example of a non–conservative force, we need look no further than some of the non–gravitational forces required to move a stone around a closed path. The person responsible for lifting and lowering the stone will certainly realize that the whole cycle can only be completed with a net exertion and will not be any the less tired for being told that no net work has been done on the stone. The muscular forces employed in lifting (and lowering) the stone will have done work on the person’s own body and the net work done by these forces will certainly not be zero. Unlike the gravitational force, these forces are not conservative.
Other examples of non–conservative forces are friction and fluid resistance (including air resistance). Fluid resistance is velocity dependent, and velocity dependent forces are generally non–conservative unless the force is always directed at right angles to the velocity, so that it does no work. i The fact that a frictional force is non–conservative can be seen from the following example.
Suppose a block is pushed through a displacement of magnitude s along a horizontal straight path from A to B and then is pushed back along the same line to its initial position A. Usually, the frictional force that acts on the block throughout its motion is of constant magnitude f. The work done on the block by the frictional force in going from A to B is −fs, since the angle between the force and the displacement is 180°. In going from B to A, the direction of the frictional force on the block is reversed, and so is the displacement, so that the work done from B to A is again −fs. Thus, the total work done over the round trip is −2fs. Since this is not zero, the friction force is not a conservative force.
Question T7
Construct an argument to explain why velocity–dependent forces should generally be expected to be non-conservative.
Answer T7
Imagine moving a particle around a closed path while a velocity–dependent force acts upon it. By moving the particle a little more quickly or a little more slowly over any small part of the path you might well expect to change the amount of work done over that part of the path without influencing the work done over the rest of the path. Consequently the work done will depend on how the path is traversed and cannot be guaranteed to be zero under all circumstances. Thus velocity–dependent forces should generally be expected to be non-conservative.
(An exception to this argument arises when the velocity–dependent force is always perpendicular to the velocity since under these circumstances the force, whatever its magnitude, will do no work. This exceptional case is of great importance in electromagnetism – see the last marginal comment.)
3.2 Potential energy
If a stone falls to the ground from rest at a height h the work done on the stone by the (conservative) gravitational force will be mgh. If we ignore air resistance, it follows from the work–energy theorem that the kinetic energy of the stone when it hits the ground will be
$\frac12 m\upsilon^2 = mgh$
If the stone is released from a greater height its final kinetic energy will be increased; if released from a lesser height the final kinetic energy will be reduced. For practical purposes the stone is behaving as if the process of lifting it to the height h somehow enables it to store energy which is released again as kinetic energy as the stone falls. This notion of stored energy as a result of position or configuration is useful in various contexts and is generally referred to as potential energy. The particular potential energy that a body has as a result of its position relative to the Earth’s surface is called its gravitational potential energy. Of course, gravitational potential energy isn’t really stored away inside the stone, rather it arises from the gravitational interaction of the Earth and the stone, and depends on their relative configuration. The gravitational potential energy associated with a particular position or configuration represents the work that the gravitational force will do on the stone when it moves from that position to the ground. It is a useful concept because the gravitational force is conservative, so the work done by the gravitational force when the stone moves from any point A to a point B on the ground is independent of the path followed from A to B.
Consequently, once a reference point has been chosen, such as a point on the ground, it is possible to assign a unique value of the gravitational potential energy to every other point. In the case of the gravitational force no work is done when a body moves horizontally so it is actually sufficient to choose a reference level (e.g. ground level) rather than a reference point, but the principle remains the same.
A potential energy that depends on position can be associated with each conservative force that acts on a body. This is because a unique amount of work is done on the body by such a force when the body is moved from any given position to a chosen reference point. This remains true irrespective of the path that is taken.
The recognition that potential energy is always associated with conservative forces leads in a natural way to a general expression for the difference in potential energy between different configurations of the system. i
The potential energy Epot of some final configuration of a system (e.g. a stone raised to a height h above the surface of the Earth) relative to a chosen reference configuration (e.g. the stone on the surface of the Earth) is equal to the work done by the associated conservative force when the system is returned from that final configuration to the reference configuration.
So, in the case of the stone, taking the vertically upwards direction to be that of the x–axis, we find:
$\displaystyle E_{\rm pot} = \int_h^0 \boldsymbol{F} \cdot d\boldsymbol{s} = \int_h^0 -mg\,dx$
i.e.Epot = mgh
In practice we can often avoid the need to define any specific reference configuration by noting that
The potential energy of a final configuration differs from that of an initial configuration by an amount ∆Epot that is equal to the negative of the work done by the conservative force when the system is taken from its initial configuration to its final configuration.
Using the subscripts i and f to represent initial and final, we can write this symbolically as follows:
(Epot)f − (Epot)i = ∆E = −Wifcon(21)
✦ For the case of the stone being moved from an initial height hi to a final height hf, write down an expression for ∆Epot in terms of a definite integral.
✧ $\displaystyle \Delta E_{\rm pot} = -W_{\rm if}^{\rm con} = -\int_{h_1}^{h_2}\boldsymbol{F}\cdot d\boldsymbol{s} = -\int_{h_1}^{h_2} - F_x\,dx = -\int_{h_1}^{h_2} -mg\,dx = \int_{h_1}^{h_2} mg\,dx$ i
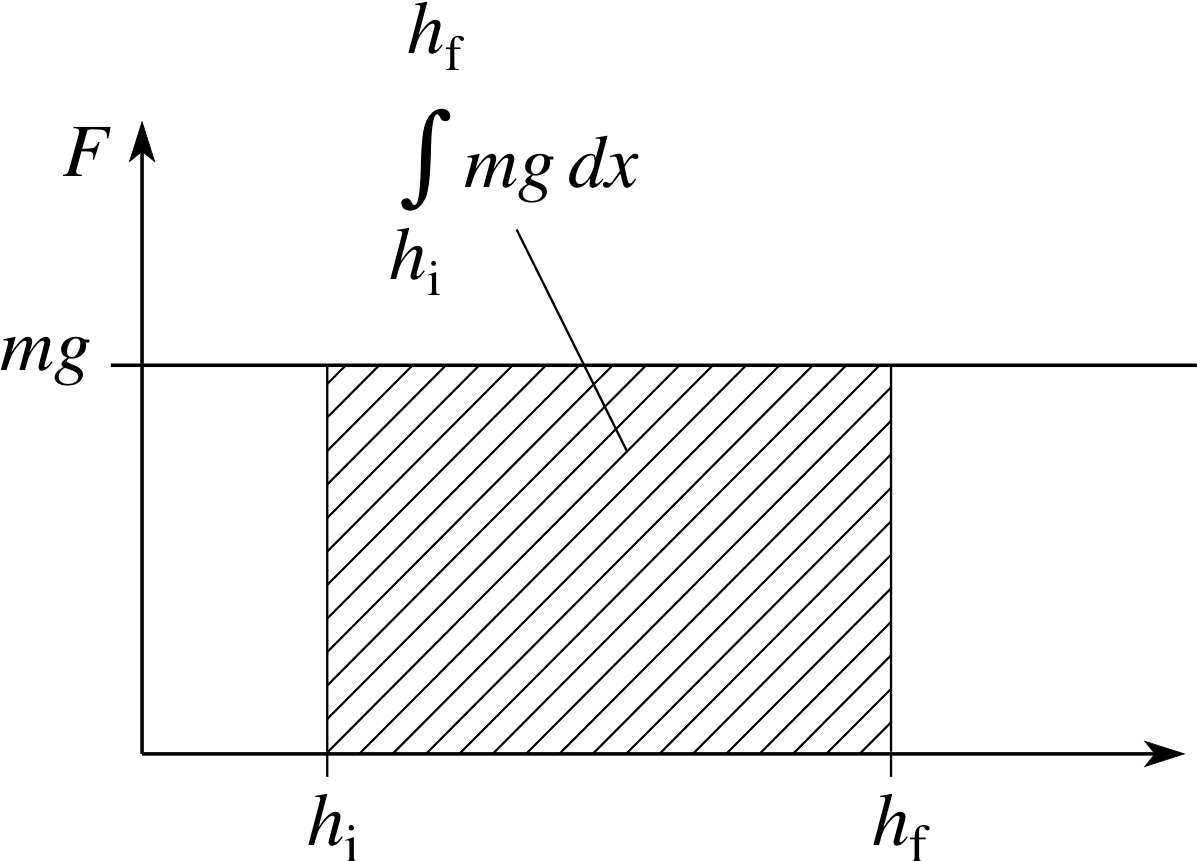
Figure 9 $\int_{h_{\rm i}}^{h_{\rm f}} mg\,dx$ interpreted as an area under a graph.
By interpreting the right hand side of Equation 21 as the rectangular area under the graph of F = mg between x = hi and hf (see Figure 9) it can be seen that in this case
for gravitational potential energy ∆Epot = mg (hf − hi)(22) i
✦ Can Epot be negative in the gravitational case?
✧ Yes, if hf is less than hi then Epot becomes negative.
Question T8
We have taken some care here to define the increase of potential energy with height in terms of the negative of the work done by the gravitational force. In many texts this increase in gravitational energy with height is described as the positive work done by the lifting force (magnitude mg upwards) acting over the positive displacement h, upwards. Give a criticism of this second approach.
Answer T8
It is only justified to relate work done and potential energy in the case of a conservative force. While the gravitational force is conservative the lifting force is unlikely to be so, e.g. it could be a muscular force or another force produced by a machine. Although the alternative approach reaches the same conclusion providing the lifting force is set equal to minus the gravitational force, the approach is unsound in principle. It raises the mass, but also the question of how the lifting begins or ends if the magnitudes of the lifting force upwards and the weight force downwards are always equal (in the face of Newton’s second law of motion)!
In Subsection 2.4 we considered the work done by an applied force in stretching or compressing an elastic body. We found that positive work was done in each case, but there was no change in the kinetic energy of the body (zero at the start and finish) because a compensating amount of negative work was done by the restoring force that arose within the body. As every child knows, a stretched or compressed elastic body may be used to create havoc by launching a projectile – catapults are ample evidence of this. The way in which the restoring force in an extended elastic body provides kinetic energy to a projectile when it is released is analogous to the way in which the gravitational force provides kinetic energy to a raised mass when it is dropped. The restoring force exerted by an ideal spring (i.e. a spring that obeys Hooke’s law) is an example of a one–dimensional conservative force, and so potential energy may be associated with such a force. The potential energy, due to the configuration of an elastic body, is called strain potential energy or simply strain energy.
The work done by the restoring force when an ideal spring that obeys Hooke’s law is extended by an amount x is −½ ksx2, where ks is the spring constant. From this it follows that the work done by the restoring force when the spring is returned from an extension x to its unextended state will be +½ ksx2. Taking the unextended state (with x = 0) as the reference configuration, it follows from the general definition of potential energy that the strain potential energy of an ideal spring extended by an amount x is
Epot = ½ ksx2(23) i
and when such a spring is extended from xi to xf
for strain potential energy ∆Epot = ½ ks(xf2 − xi2)
✦ Can Epot for a spring be negative?
✧ No. Epot is proportional to x2, and so must be positive, even if x becomes negative, as occurs when the spring is compressed.
Finally, it should be stressed that the potential energy Epot that we have been discussing in this subsection is really just another difference in potential energies, like ∆Epot. It is ‘special’ only in the sense that it represents the difference from the potential energy of the selected reference configuration of the system. We are actually free to assign any value we want to the potential energy E0 of the reference configuration, with the consequence that the total potential energy of any other configuration will then be Epot + E0. Because of our freedom to choose E0 to be whatever we want, these total values have no physical significance. In practice we choose E0 for our own convenience, which usually means choosing it to be zero.
Question T9
By how much must an ideal spring with ks = 100 N m−1 be stretched from its unextended position to give it the same potential energy as a 2 kg mass raised to a height of 1.20 m above the reference level at which Epot = 0? (Take g = 9.81 m s−2)
Answer T9
Spring potential energy is given by ½ ksx2; whereas gravitational potential energy is given by mgh. Therefore, for these to be the same:
½ ksx2 = mgh
So,x = (2mgh/ks)1/2 = (2 × 2 kg × 9.81 m s−1 × 1.20 m/100 N m−1)1/2 ≈ 0.69 m
3.3 Conservation of mechanical energy
In the work–energy theorem of Subsection 2.3 we saw that the work done on a particle of mass m by any resultant force F (conservative or not) is equal to the change in kinetic energy of the particle. This result was summarized in Equation 12:
W = (Etran)f − (Etran)i(Eqn 12)
In Equation 21 of Subsection 3.2
(Epot)f − (Epot)i = ∆E = −Wifcon(Eqn 21)
we saw that the work done by a conservative force when a system is taken from an initial configuration to a final configuration is:
Wifcon = −[(Epot)f − (Epot)i] = (Epot)i − (Epot)f
If we restrict our discussion to a system of particles acted upon by conservative forces (so that both Equations 12 and 21 are valid), and not subject to any additional external force, i we can equate these two amounts of work and hence obtain:
(Epot)i − (Epot)f = (Etran)f − (Etran)i
i.e.(Epot + Etran)i = (Epot + Etran)f
If we define the total mechanical energy Emech of a particle to be the sum of its potential and kinetic energies, then we can say that
Provided the only forces which act on a system are conservative forces, and provided no additional external forces are allowed to act
Emech = Epot + Etran = constant(24)
In other words, the total mechanical energy is constant unless work is done by some additional force. This result is known as the principle of conservation of mechanical energy, and is an example of a conservation_principle_or_lawconservation principle. Note that the principle applies when only conservative forces act and for an isolated system, in which there are no external forces acting or energy exchanges with any external system. i
This principle provides a means of relating the speed of an object to its position, and plays an important part in the solution of many problems in mechanics.
Question T10
A block of mass 1 kg is released from rest in vacuum and falls on to the top of a spring, which is standing vertically on a firm surface. If the total distance travelled by the block is 5.50 m when the spring is suffering maximum compression, find the maximum compression of the spring, and the speed of the block when the it first hits the spring. The spring constant is 299 N m−1. (Take g = 9.81 m s−2).
Answer T10
Let the reference level for gravitational potential energy correspond to maximum compression, x, of the spring. If h is the total distance fallen by the block at maximum compression, then, using the principle of conservation of mechanical energy (gravitational energy is converted into strain energy of the spring):
½ ksx2 = mgh
So,x = (2mgh/ks)1/2 = (2 × 1 kg × 9.81 m s−2 × 5.50 m/299 N m−1)1/2 ≈ 0.60 m
Therefore, the distance fallen when the block first hits the spring is:
h − x ≈ (5.5 − 0.6) m ≈ 4.9 m
Using the principle of conservation of mechanical energy:
½ mυx2 = mg (h − x)
where υx is the speed of the block when it has fallen a distance (h − x)
υx = [2g (h − x)]1/2 ≈ (2 × 9.81 m s−2 × 4.9 m)1/2 ≈ 9.8 m s−1
3.4 Conservative forces and potential energy functions
In the examples we have considered so far, potential energy has always been related to the x–coordinate of position in some unique way. In other words, the potential energy has always been a function of x, and could have been written Epot(x) to remind us of this. i) So far, we have obtained potential energy functions from the relevant conservative force, but we can do the opposite and obtain the conservative force from the potential energy function. From Equation 21 in Subsection 3.2 we see that the work done by a conservative force is the negative of the change in the corresponding potential energy.
Wifcon = −[(Epot)f − (Epot)i] = ∆Epot
Let us apply this to the case in which a conservative force F = (Fx, Fy, Fz) acts on a particle initially located at the point (x, y, z) while it undergoes a small displacement ∆s = (∆x, ∆y, ∆z). We will assume that the displacement is sufficiently small that F can be taken to be approximately constant throughout the displacement. The work done by F over ∆s is then approximately given by
Wifcon ≈ F ⋅ ∆s = Fx∆x + Fy∆y + Fz∆z
and the corresponding change in the potential energy is approximated by
−∆Epot ≈ Fx ∆x + Fy ∆y + Fz ∆z(25)
For the sake of simplicity we will assume that Epot depends only on x, even though the displacement may be fully three–dimensional (this was the case with the gravitational potential energy we considered earlier). We can then say that
−∆Epot ≈ Fx ∆x
i.e.Fx ≈ −∆Epot /∆x
If we take the limit of this expression as ∆x tends to zero then the approximation will become an equality and we can use the notation of differential calculus to write:
$\displaystyle F_x = \lim_{\Delta x\rightarrow 0} \left(\dfrac{-\Delta E_{\rm pot}}{\Delta x}\right) = -\dfrac{dE_{\rm pot}}{dx}$(26) i
where the derivative on the right–hand side may be interpreted graphically as the gradient (i.e. slope) of a graph of Epot against x at the particular value of x that corresponds to the instantaneous position of the particle. Because of this identification we often summarize the important result given in Equation 26 by saying
Force is minus the gradient of potential energy.
Applying this to the case of the ideal spring, for which Epot = ½ ksx2
we see that $F_x = -\dfrac{dE_{\rm pot}}{dx} = - \dfrac{d}{dx}\left(\dfrac12 k_sx^2\right)$
If you evaluate the derivative (by drawing the graph of Epot against x and measuring its gradient, or by using the techniques of differentiation which are developed elsewhere in FLAP) you will find that
Fx = −ksx
You should recognize this as the correct answer, since it expresses Hooke’s law, which applies in this case, in terms of the (conservative) restoring force that arises from the tension.
Question T11
Use the fact that the gravitational potential energy of a particle of mass m at a height h above the Earth’s surface is Epot = mgh to find the gravitational force that acts on that particle.
Answer T11
If we introduce an x–axis that points vertically upwards with x = 0 coincident with h = 0, we can rewrite E2 = mgh in the form E2 = mgx. From Equation 26,
$\displaystyle F_x = \lim_{\Delta x\rightarrow 0} \left(\dfrac{-\Delta E_{\rm pot}}{\Delta x}\right) = -\dfrac{dE_{\rm pot}}{dx}$(Eqn 26)
it then follows that Fx is given by:
$F_x = -\dfrac{dE_{\rm pot}}{dx} = -\dfrac{d}{dx}(mgx)$
i.e. Fx is the gradient of the graph of mgx against x. Since this is a straight line its gradient is
Fx = −mg
In three–dimensional terms Fgrav = (−mg, 0, 0)
Comment Instead of introducing an appropriate x–axis we could have solved this problem by rewriting Equation 26 in the form Fh = −dEpot/dh.
Some of the most important conservative forces that arise in physics are central forces, that is to say the force is always directed towards a point (called the force centre) and has a magnitude that depends on the distance r from that force centre. i
Outstanding examples of such forces are the gravitational force that one particle exerts on another, as described by Newton’s law of gravitation, and the electrical force that one charged particle exerts on another. In both these cases the force is described by an inverse square law of the form
Fr = k/r2(27)
where the component Fr points radially outwards from or inwards towards the force centre, and k is a constant that may be positive or negative. Central forces of this or any other sort are always conservative and may be associated with a potential energy that depends on r. In the case of an inverse square law this potential energy is of the form
Epot = k/r(28)
where the reference configuration with Epot = 0 is that in which the distance from the force centre, r, approaches infinity.
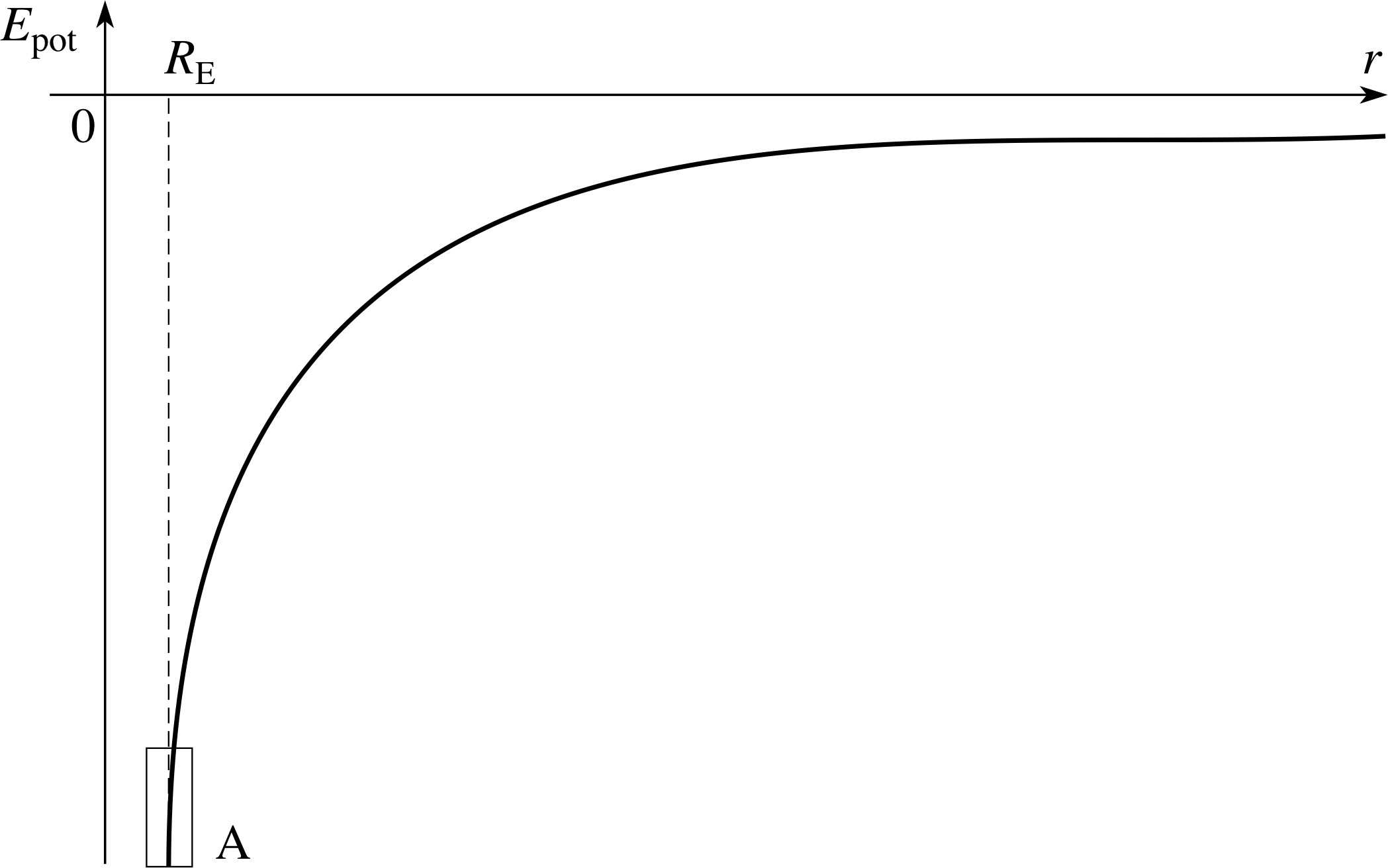
Figure 10 The gravitational potential energy of a fixed mass m at a distance r from the centre of the Earth.
For instance, in the case of the gravitational force between two particles of masses M and m separated by a distance r (the full expression for the force, not the approximation of constant weight that applies close to the Earth’s surface) the constant k has the value −GMm, where G is Newton’s gravitational constant i, so the associated gravitational potential energy is
$E_{\rm pot} = \dfrac{-GMm}{r}$(29a)
and$F_{r} = -\dfrac{dE_{\rm pot}}{dr} = \dfrac{-GMm}{r^2}$(29b)
If we set M = ME, the mass of the Earth, and consider r ≥ RE, the radius of the Earth, then Equations 29a and 29b provide a good approximation to the gravitational potential energy and radial force component on a body of mass m at a radial distance r from the centre of the Earth. This gravitational potential energy is shown in Figure 10.
You might be somewhat surprised that Equation 29 describes the gravitational force and potential on a body. After all, until we started this discussion of central forces we had always said that for a body near the Earth
Epot = mgh and Fx = −mg i
which is difficult to compare with Epot = −GMm/r since only Epot and m are common to both equations. However remember, these two equations only apply close to the Earth, where r ≈ RE.
If you look at the small box that covers this region, near point A in Figure 10, you will see that the gravitational potential energy is approximately linear in that region. So we can use the linear relation Epot = mgh (and consequently Fx = −mg) to describe gravityterrestrial gravity, provided we also change the reference position from which we measure the potential energy. When using Epot = mgh we assume Epot = 0 at the surface of the Earth, where h = 0. But when using Epot = −GMEm/r we are assuming Epot = 0 as r tends to infinity. Naturally, we should not expect the terrestrial approximations to work if we consider changes in height that are substantial compared with the radius of the Earth.
✦ What specific feature of Figure 10 can be determined from the fact that the gravitational potential energy close to the Earth’s surface is well–approximated by Epot = mgh?
✧ The gradient of the line inside the box is mg.
Aside In this subsection we have only considered potential energy functions that depend on a single variable, such as Epot(x) and Epot(r). However, in general the potential energy may depend on several variables, such as Epot(x, y, z). In such cases the relation between Fx and Epot given in Equation 26,
$\displaystyle F_x = \lim_{\Delta x\rightarrow 0} \left(\dfrac{-\Delta E_{\rm pot}}{\Delta x}\right) = -\dfrac{dE_{\rm pot}}{dx}$(Eqn 26)
has to be modified to some extent, along with the similar formulae that relate Fy and Fz to Epot. These modifications involve a technique known as partial differentiation which is not particularly difficult but is beyond the scope of this module.
3.5 Non–conservative forces and mechanical energy
The principle of conservation of mechanical energy,
Emech Epot + Etran = constant(Eqn 24)
enables us to establish the relation between position and speed, when we have an isolated system of particles acted upon only by conservative forces. What happens if non–conservative forces are present? For example, suppose a block descends a vertical distance from rest by sliding down a rough inclined plane. In this case, a non–conservative frictional force acts on the block, so we would expect that the final speed of the block will be less than that obtained if no such frictional force existed. Let us now consider how the principle of conservation of mechanical energy has to be modified to account for such cases.
The work–energy theorem (Equation 12) applies to the action of any resultant force, be it conservative or not, and this tells us that the total work done on the block is related to the kinetic energy change by:
W = (Etran)f − (Etran)i(Eqn 12)
If the force is conservative then the work done also relates to the change in potential energy through Equation 21:
(Epot)f − (Epot)i = ∆E = −Wifcon(Eqn 21)
Suppose now that the total work done W includes a contribution Wcon from conservative forces and a contribution Wnc from non–conservative forces.
W = W con + W nc(30)
Substituting Equations 12 and 21 into this expression gives:
(Etran)f − (Etran)i = −[(Epot)f − (Epot)i] + W nc
i.e.(Etran)f + (Epot)f = (Etran)i + (Epot)i + W nc
so from Equation 24:
Emech = Epot + Etran = constant(Eqn 24)
(Emech)f = (Emech)i + W nc (31)
From Equation 31 we see that if positive work is done on the body by the non–conservative force(s) as the body travels from its initial position to its final one, then the final total mechanical energy is greater that the initial total mechanical energy. However, if negative work is done by the non–conservative forces, then the final total mechanical energy is less than the initial value. Let us apply this result to our example of the block sliding down the plane.
Example 1
Suppose a block of mass 5 kg slides from rest down an inclined plane of length 8 m, and in so doing descends a vertical distance of 2 m. Evaluate the speed of the block at the bottom of the incline assuming (a) no friction, and (b) that a frictional force of magnitude 4 N acts on the block.
Solution i
(a) Let m be the mass of the block, which starts from rest and descends a vertical distance h, reaching a speed υ1. Using the principle of conservation of mechanical energy, as in Equation 24,
$\frac12 m\upsilon_1^2 = mgh$
so$\upsilon_1 = \sqrt{2gh\os} = \rm \sqrt{2\times9.8\,m\,s^{-2}\times2\,m} \approx 6.3\,m\,s^{-1}$
(b) Let the displacement down the incline be s, the final speed be υ2 and the frictional force f, which is directed up the incline. Equation 31,
(Emech)f = (Emech)i + Wnc (Eqn 31)
gives:
$\frac12 m\upsilon_2^{\,2} = mgh - fs$
so$\upsilon_2 = \sqrt{2gh - 2fs\os} = \rm \sqrt{(2\times 9.8\,m\,s^{-2}\times 2\,m) - \dfrac{2\times 4\,N\times 8\,m}{5\,kg}} \approx 5.1\, m\,s^{-1}$
As expected, the speed of the block at the bottom of the incline is less when a frictional force is present than when no frictional force exists.
3.6 Conservation of energy
In the last subsection we saw that when non–conservative forces do work the mechanical energy of a system is not conserved. i In the example of the block sliding down the plane, we saw that the final kinetic energy of the block was lower when friction was present than when it was absent. What has happened to the kinetic energy which was lost when friction was present? Experiment shows that the work done by the friction force results in an increase of temperature of the surfaces involved. This is a manifestation of another form of energy, which we call thermal_kinetic_energythermal energy. i This thermal energy is actually the energy associated with the kinetic and potential energies of the vibrating molecules of the materials of the block and the plane and is part of the internal energy of those objects.
So, it appears that although some bulk mechanical energy has been lost by the block, this loss is matched by the gain in thermal energy, and the total energy of our system has not altered. We can extend this idea further to include all other types of energy, including chemical energy, electrical energy, nuclear energy and mass energy, as we will see shortly.
Consider an isolated system, in which no energy exchange occurs between the system and its surroundings. We can evaluate the total energy of the system by adding together the energies associated with all the various energy forms. If we repeat this process at various times we find that the total energy remains constant, although the contributions to the total energy from the various forms may change with time as energy is transformed from one form to another. This result is embodied in the principle of conservation of energy which may be stated as follows:
Although energy can change from one form to another, the total energy of an isolated system remains constant.
The principle of conservation of energy is one of the most important in the whole of science. It prohibits many processes which might otherwise seem plausible (such as various types of perpetual motion) and provides a firm constraint on those processes which do occur. The principle emerged from the work of a number of 19th century physicists, notably Julius Robert von Mayer (1814–1878) i and Hermann Ludwig von Helmholtz (1821–1894), though a new aspect of the concept was introduced in 1905 when Albert Einstein (1879–1955) developed his special theory of relativity.
Einstein deduced that the mass of a body is a measure of its energy content. Thus, when a body is heated its mass will increase slightly, and, more significantly, even when a body is at rest and has no potential energy, it still has a certain amount of mass energy as given by einsteins_mass_energy_equationEinstein’s equation
$E = mc^2$(32)
where c is the speed of light in a vacuum. i The inclusion of mass energy as just another form of energy to be taken into account in the conservation of energy allows for the interconversion of mass and energy; mass can be transformed into energy, and energy can be transformed into mass. This is demonstrated most clearly in nuclear reactions as described elsewhere in FLAP.
Question T12
What would be the mass equivalent of the energy needed to keep an electric fire that consumed 1000 J of electrical energy per second running for 1 day?
Answer T12
From Einstein’s equation, E = mc2, so m = E/c2, where, in this case, E is equal to the energy consumed per second multiplied by the number of seconds in a day. The mass equivalent is therefore:
m = 1000 J s−1 × (24 × 60 × 60) s/(3 × 108 m s−1)2 = 9.6 × 10−10 kg
A little mass goes a long way!
4 Power
When calculating the work done by a force we are not usually concerned with the time taken, but when we wish to compare the capabilities of two machines for performing a particular task, we are very often concerned with how quickly they can provide a certain amount of work. This means that the simple quantity ‘work done’ is not sufficient for measuring the performance of a machine. What is often more useful as an indicator of performance is the rate at which work is done, that is the amount of work that can be done per unit time. This quantity is called the power.
The SI unit of power, the joule per second (J s−1) is usually called the watt (W), in honour of James Watt (1736–1819) the Scottish engineer who pioneered the development of the steam engine. The kilowatt (1 kW = 103 W) is also commonly used. Watt himself originally introduced the idea of horsepower (hp) as the unit of power. This non–SI unit is still used in some engineering circles, and a useful conversion factor to remember for everyday purposes is: 1 hp = 746 W = 0.746 kW.
4.1 Average and instantaneous power
Suppose you pull a heavy trolley and do 400 J of work in 10 s in moving the trolley through a certain displacement.
The average rate of working is 400 J/10 s = 40 W. In general we define the average power $\langle P\rangle$ for an amount of work done ∆W in a time interval ∆t by
$\langle P\rangle = \Delta W/\Delta t$(33) i
The rate at which work is done may not be constant over ∆t, and it is often important to know this rate at a given instant of time. This instantaneous power, which is what is usually meant by the unqualified term power, is defined as the limit of ∆W/∆t as ∆t tends to zero. Expressing this as a derivative we have:
instantaneous power P = dW/dt(34)
✦ What are typical values for the power ratings of the following household items: a tungsten light bulb, a colour television, an immersion heater, an electric toaster, a vacuum cleaner?
✧ Bulb, 40 W, 60 W or 100 W; colour television, 100 W; immersion heater, 3 kW; electric toaster, 1 kW; vacuum cleaner, 1 kW.
Units of power can be used to define alternative units for work or energy. From Equation 33 we see that ∆W can be expressed as:
$ \Delta W = \langle P\rangle/\Delta t$
This means that we could use the watt–second (W s) instead of the joule as an SI unit of work or energy. In practice this watt–second unit is rarely used, but the kilowatthour (kW h) is commonly used as the commercial unit for the measurement of electrical energy consumption. One kilowatthour is the energy consumed or work done in one hour when the power is 1 kW.
1 kW h = 103 J s−1 × 3600 s = 3.6 × 106 J = 3.6 MJ
✦ Compare the energy consumed by a 1 kW electric fire in 45 min with that consumed by a 60 W light bulb in 12 h.
✧ Electric fire consumption: 1 kW × 0.75 h = 0.75 kW h
Light bulb consumption: 0.06 kW × 12 h = 0.72 kW h
Thus the energy consumption of the two are approximately the same.
4.2 Power as a scalar product
An alternative expression for power to that given in Equation 33,
$\langle P\rangle = \Delta W/\Delta t$(Eqn 33)
can be developed in terms of a force F doing work on a body that moves with velocity υ. The work done by F over a small displacement ∆s is:
∆W = F ⋅ ∆s
The average power delivered by that force over the time ∆t is given by:
$\langle P\rangle = \Delta W/\Delta t = (\boldsymbol{F} \cdot \Delta\boldsymbol{s})/\Delta t = \boldsymbol{F} \cdot (\Delta\boldsymbol{s}/\Delta t)$
The instantaneous power is given by the limit of this as ∆t tends to zero:
P = dW/dt = F ⋅ (ds/dt) = F ⋅ υ(35)
Question T13
What is the rate at which work is done by a force F acting on a body which is moving in a direction perpendicular to F? i
Answer T13
From Equation 35,
P = dW/dt = F ⋅ (ds/dt) = F ⋅ υ(Eqn 35)
it can be seen that P = Fυ cos θ, where θ is the angle between F and υ. Since θ = 90° in this case, cos θ is zero and hence P is zero also. Thus a force acting normal to the direction of motion delivers no power and therefore does not change the kinetic energy. This is the situation for an object moving in a circle at constant speed, since such an object must be subject to a force of constant magnitude that is always directed towards the centre of the circle.
5 Applications
In this section we examine two applications of the concepts and results regarding work, energy and power that we have met in the earlier sections.
5.1 Collisions in one dimension
In a scientific context, the term collision means a brief but powerful interaction between two particles or bodies. Collisions may be categorized by comparing the total kinetic energy of the colliding bodies before the collision with their total kinetic energy after the collision. If there is no change in the total kinetic energy then the collision is said to be an elastic collision. If the kinetic energy after the collision is less than that before the collision then the collision is said to be an inelastic collision.
In general, collisions between macroscopic objects are inelastic but some collisions, such as those between steel ball bearings or between billiard balls, are very nearly elastic. Collisions between subatomic particles, such as electrons, protons, etc., are often elastic. The kinetic energy which is lost in an inelastic collision appears as energy in a different form, e.g. thermal energy, sound energy, light energy, etc., so that the total energy is conserved. If the bodies stick together on collision, and move off together after the collision, the collision is said to be completely inelastic. In this case a maximum amount of kinetic energy is converted into other forms of energy.
Let us consider the example of a collision in one dimension between particles of mass m1 and m2 which are moving with initial speeds u1 and u2 in the same horizontal direction before the collision. We will call the speeds after the collision υ1 and υ2. If the collision is elastic the kinetic energy is conserved and we can write:
$\dfrac12 m_1u_1^2 + \dfrac12 m_2u_2^2 = \dfrac12 m_1\upsilon_1^2 + \dfrac12 m_2\upsilon_2^2$(36)
Even if we know the values of m1, m2, u1 and u2, this single equation is insufficient for us to determine the two unknown values, υ1 and υ2. To evaluate two unknowns requires two independent equations and kinetic energy conservation in an elastic collision gives only one equation, as above. These collision problems require another conservation principle to supply one further equation involving υ1 and υ2.
This is the principle of conservation of linear momentum, which is discussed elsewhere in FLAP.
5.2 Escape speeds
If we throw a stone vertically upwards it reaches a certain height and then falls back again. If we throw it again, with a greater initial speed, it will reach a greater height before returning. This suggests that if we could launch the stone with sufficient initial speed it would be able to leave the Earth entirely and escape to infinity. In fact this is a correct conclusion, and the minimum speed required to achieve this is called the escape speed.
We saw earlier, using Equation 29a,
$E_{\rm pot} = \dfrac{-GMm}{r}$(Eqn 29a)
that the gravitational potential energy of a body of mass m at a distance r from the centre of the Earth is:
$E_{\rm pot} = \dfrac{-GM_{\rm E}m}{r}$(Eqn 37)
where ME represents the mass of the Earth, and G is Newton’s gravitational constant.

Figure 10 The gravitational potential energy of a fixed mass m at a distance r from the centre of the Earth.
This potential energy function was shown graphically in Figure 10. Notice that since r is positive Epot must always be negative, but it becomes less negative (i.e. it increases) as r increases. Indeed, as the separation tends to infinity the value of Epot tends to zero. On the surface of the Earth, where r = RE, it follows that Epot = −GmME/RE.
Let us now use this expression for gravitational potential energy together with the concept of conservation of mechanical energy to determine the escape speed of a body. This is the minimum speed with which a body can be projected from the surface of the Earth to enable it just to escape from the Earth and reach r = ∞ with zero speed. This means that the total mechanical energy at r = ∞ is zero, and so the initial total mechanical energy at r = RE also must be zero:
i.e.$(E_{\rm mech})_{\rm i} = \left(\dfrac12 m\upsilon_{\rm es}^2\right) - \dfrac{GmM_{\rm E}}{R_{\rm E}} = 0$
where υes is the required escape speed from the Earth’s surface.
It follows that
υes = (2GME/RE)1/2(38)
It is interesting to note that the escape speed is independent of the mass of the escaping body. However, the initial kinetic energy required to give a body the required escape speed is directly proportional to the mass of the body.
✦ Determine the value υes from Earth given that G = 6.67 × 10−11 N m2 kg−2, ME = 5.98 × 1024 kg and RE = 6.37 × 106 m.
✧ Substituting values into Equation 38,
υes = (2GME/RE)1/2
we find:υes = 11.2 × 103 m s−1.
Question T14
A body is projected vertically with a speed equal to half the escape speed. Determine the maximum height reached, in terms of the radius of the Earth RE. (Neglect air resistance.)
Answer T14
Let the maximum height reached be h. The initial total mechanical energy at the surface of the Earth is given by:
$(E_{\rm mech})_{\rm i} = \dfrac12m\left(\dfrac{\upsilon_{\rm es}}{2}\right)^2 - \dfrac{GmM_{\rm E}}{R_{\rm E}}$
Since the body will be at rest the final total mechanical energy at the height h is:
$(E_{\rm mech})_{\rm f} = 0 - \dfrac{GmM_{\rm E}}{R_{\rm E}+h}$
Equating these two energies:
$\dfrac{GmM_{\rm E}}{R_{\rm E}+h} = \dfrac{GmM_{\rm E}}{R_{\rm E}} - \dfrac{m\upsilon^2_{\rm es}}{8}$
Butυes2 = 2GME/RE(Eqn 38)
so$\dfrac{GmM_{\rm E}}{R_{\rm E}+h} = \dfrac{GmM_{\rm E}}{R_{\rm E}} - \dfrac{2GmM_{\rm E}}{8R_{\rm E}}$ i.e. (RE + h) = 4RE/3
thush = RE/3
6 Closing items
6.1 Module summary
- 1
-
The work done by a constant force F on a body that undergoes a displacement s is defined by the scalar product
W = Fxsx + Fysy + Fzsz = Fs cos θ = F ⋅ s(Eqn 5)
If the force is not constant, then this product is replaced by the limit of an appropriate sum, which may be expressed as a definite integral. In the case of a force that varies in strength but always acts along the x–axis this integral takes the form
$\displaystyle W = \int_{x_{\rm A}}^{x_{\rm B}} F_x(x)\,dx $(Eqn 16)
which may be interpreted as the area under the graph of Fx against x between xA and xB. In three dimensions the work done may depend on the particular path that the body moves along can be represented by the line integral
$\displaystyle W = \int_{x{\rm A}}^{x_{\rm B}} \boldsymbol{F} \cdot d\boldsymbol{s}$
- 2
-
The translational kinetic energy of a body of mass m and speed υ is:
Etran = ½ mυ2(Eqn 10)
and the work done on a body by a single resultant force can be related to the change in kinetic energy of the body, by the work–energy theorem:
W = (Etran)f − (Etran)i = ∆Etran(Eqn 12)
- 3
-
A conservative force is one where the total work done by the force is zero for any round trip, or where the work done by the force is independent of the path connecting the start and end points. Other forces are non-conservative forces.
- 4
-
A potential energy may be associated with each conservative force that acts on a body or between a system of bodies. The amount of potential energy associated with some final configuration (relative to a chosen reference configuration) is known as Epot. This is equal to the work done by the conservative force on the system as it is taken from that final configuration to the chosen reference configuration. Equivalently, we can say that it is the negative of the work done by the conservative force as the system is taken from some initial configuration to the final configuration.
(Epot)f − (Epot)i = ∆E = −Wifcon(Eqn 21)
The gravitational potential energy of a mass m at a small height h above the Earth’s surface is given by:
Epot = mgh i
The gravitational potential energy of a mass m at a distance r from the Earth’s centre is given by:
$E_{\rm pot} = \dfrac{-GM_Em}{r}$(Eqn 37) i
The strain potential energy of a spring that obeys Hooke’s law that has been extended by an amount x from its unextended state is given by
Epot = ½ ksx2(Eqn 23) i
- 5
-
For systems in which only conservative forces act, the total mechanical energy, Emech, is conserved. That is:
Emech = Epot + Etran = constant(Eqn 24)
where Epot and Etran are the potential and translational kinetic energies of the system. This equation provides the means of linking the speed of a body to its position in such a system.
For systems in which non–conservative forces act, the total mechanical energy, Emech, is not conserved, but varies with the work done as:
(Emech)f = (Emech)i + Wnc(Eqn 31)
- 6
-
If the potential energy associated with a particular conservative force is a function of the single variable x, then the only non–zero component of the force will be Fx, and its value at any point will be given by the negative gradient of the Epot against x graph at the same point.
$\displaystyle F_x = \lim_{\Delta x\rightarrow 0} \left(\dfrac{-\Delta E_{\rm pot}}{\Delta x}\right) = -\dfrac{dE_{\rm pot}}{dx}$(Eqn 26)
- 7
-
The principle of conservation of mechanical energy can be extended to cover all forms of energy, thus leading to the principle of conservation of energy. The idea that mass is a measure of energy content, as suggested by Einstein, has to be incorporated into this principle to make it universal.
- 8
-
Power is defined as the rate of doing work:
P = dW/dt(Eqn 34)
Power is related to the force F exerted on a body moving with velocity υ by means of the scalar product:
P = F ⋅ υ(Eqn 35)
- 9
-
In an elastic collision the total kinetic energy is conserved.
6.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Write down expressions for work done by a force acting upon a body when the body undergoes a specified displacement or moves along a specified path. (This applies to cases in which the force varies as well as cases in which it is constant.)
- A3
-
Write down and justify an expression for the work done by a force in stretching a spring that obeys Hooke’s law.
- A4
-
State the work–energy theorem, derive an equation which represents that theorem in sufficiently simple cases, and use that equation to solve problems involving work done and kinetic energy changes.
- A5
-
Distinguish between conservative and non–conservative forces and explain why the concept of potential energy is meaningful only in relation to conservative forces.
- A6
-
Derive expressions for gravitational potential energy near the Earth’s surface and the potential energy of a stretched or compressed spring in sufficiently simple cases. (This might involve writing down integrals, but you are not expected to evaluate those integrals in this module unless you can do so graphically.)
- A7
-
Derive an expression which represents the principle of conservation of mechanical energy and solve problems using this conservation principle.
- A8
-
Recall the relation between a conservative force and the associated potential energy function, and use it to obtain the force from a given potential energy function in sufficiently simple cases. (In this module this is limited to cases in which the potential energy is a function of a single variable.)
- A9
-
Explain the meaning of the term power and describe the use of this quantity in comparing the performances of machines.
- A10
-
Recall and derive an expression relating power, force and velocity.
- A11
-
Describe how the concept of conservation of mechanical energy can be extended to cover all forms of energy and how this leads to the principle of conservation of energy.
- A12
-
Distinguish between elastic and inelastic collisions.
- A13
-
Write down and use a general expression for the gravitational potential energy of two point like masses separated by a given distance. Use this expression to justify a formula for the escape speed from the Earth.
Study comment You may now wish to take the Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
6.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
Explain the meaning of the term work done in the context of a constant force, and determine the work done by a force of magnitude 5 N acting on a particle which undergoes a displacement of 3 m, if the angle between the force and the displacement is: (a) 0°, (b) 53.1°, (c) 90°.
Answer E1
Work is done by a constant force if the force has a component in the direction of the displacement of the body on which the force acts. Work done W = F ⋅ s = Fs cos θ, where θ is the angle between the force and the displacement.
(a) when θ = 0°, W = 5 N × 3 m × cos 0° = 15 J
(b) when θ = 53.1°, W = 5 N × 3 m × cos 53.1° = 9 J
(c) when θ = 90°, W = 5 N × 3 m × cos 90° = 0 J
(Reread Subsection 2.1 if you had difficulty with this question.)
Question E2 (A3)
The same amount of work is done in stretching springs A and B by extensions 2x and x, respectively. If both springs obey Hooke’s law, what is the ratio of the spring constants of springs A and B?
Answer E2
½ kA (2x)2 = ½ kBx2
sokA/kB = 1/4
(Reread Subsection 2.4 if you had difficulty with this question.)
Question E3 (A4)
Show that the work done by a constant force on a particle is equal to the increase in kinetic energy of the particle.
Answer E3
Use Fx = max and the constant acceleration equation υx2 = ux2 + 2axsx to show that:
Fxsx = ½ mυx2− ½ mux2
Full details are given in Subsection 2.3.
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E4 (A10)
A single force acts on particle moving in one dimension, causing it to accelerate. If power is supplied by the force at the constant rate of 20 W, what is the magnitude of the force when the speed of the particle is 8 m s−1?
Answer E4
From Equation 35, P = F ⋅ υ, and in this case P = Fυ.
ThusF = P/υ = 20 W/8 m s−1 = 2.5 N
(Reread Subsection 4.1 if you had difficulty with this question.)
Question E5 (A5)
Explain the difference between a conservative and a non–conservative force; explain the meaning of the term potential energy. How are these concepts related?
Answer E5
A force acting on a body is conservative if the total work done by the force on the body is zero for any round trip made by the body. (Alternatively, the work done by the force when the body moves between any two points is independent of the path followed by the body.) Non–conservative forces do not fulfil these conditions. Conservative forces do not cause mechanical energy to be dissipated as ‘heat’ or in any other form. Potential energy is the energy associated with position or configuration, and is ‘stored’ energy that can be retrieved. The concept of potential energy is meaningful only when associated with conservative forces. The change in potential energy in going from some given initial configuration of a system to some final configuration is equal to the negative of the work done by the conservative forces that operate within that system in going from the initial to the final configuration:
(Epot)f − (Epot)i = −Wifcon
(Reread Subsections 3.1 and 3.2 if you had difficulty with this question.)
Question E6 (A8)
The potential energy function associated with a central force directed towards a fixed point O is given by: Epot = kr, where r is the distance from O and k is a constant. Find an expression for the force in terms of r and k.
Answer E6
The force may be completely specified by its radial component Fr which is directed away from O, and it follows from Equation 29b
$F_{r} = -\dfrac{dE_{\rm pot}}{dr} = \dfrac{-GMm}{r^2}$(29b)
that Fr = −dEpot/dr. Thus, for the given potential energy function,
$F_r = - \dfrac{d}{dr}(kr)$
This derivative represents the gradient of the graph of kr against r. Since this is a straight line graph of constant gradient k, it follows that Fr = −k. Thus the force has the same magnitude everywhere and is directed towards O if k is positive.
(Reread Subsection 3.4 if you had difficulty with this question.)
Question E7 (A4 and A11)
A block of mass m projected with speed u across a rough horizontal surface comes to rest in a distance d. Explain what happens to the kinetic energy lost by the block and derive an expression for the magnitude of the (constant) frictional force acting on the block.
Answer E7
Almost all the kinetic energy is converted into thermal energy (or ‘heat’), which causes the temperatures of the surfaces in contact to increase temporarily. The work done by the friction force is equal to the change in the kinetic energy of the block. If the magnitude of that force is f
−fd = 0 − mu2/2
so,f = mu2/2d
(Reread Subsection 3.6 if you had difficulty with this question.)
Question E8 (A12)
A particle of mass 2m, travelling with speed u1, makes an elastic collision with another particle of mass m and speed u2. Determine the total kinetic energy after the collision.
Answer E8
In an elastic collision the total kinetic energy is conserved. The final and initial kinetic energies are the same and equal to:
Etran = ½ (2m)u12 + ½ mu22 = ½ m (2u12 + u22)
(Reread Subsection 5.1 if you had difficulty with this question.)
Question E9 (A13)
The Moon has a mass of 6.84 × 1022 kg and radius 1.74 × 106 m. Calculate the escape speed from the lunar surface.
Answer E9
The escape speed is given by an equation similar to Equation 38:
$\begin{align} \upsilon_{\rm es} & = \left(\dfrac{2GM}{R}\right)^{1/2}\\ & = \rm \left(\dfrac{2\times 6.67\times 10^{-11}\,N\,m^2\,kg^{-2}\times6.84\times10^{22}\,kg}{1.74\times10^6\,m}\right)^{1/2} \approx 2.29\times 10^3\,m\,s^{-1}\end{align}$
(Reread Subsection 5.2 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 6Closing items.