PHYS 2.3: Forces |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
This module is concerned with dynamics – the study of forces and their effects on the motion of bodies. Many of the terms we need in this module are used in everyday life in rather imprecise, and sometimes contradictory, ways. One of our main tasks in dynamics is to give precise meanings to terms such as mass, weight, speed, velocity, force and acceleration. While it may seem pedantic to do this, it is crucial if we are to make this study of motion quantitative and predictive – essential aspects of science. If scientists are to land a spacecraft on the Moon, they must do far more than just talk about it!
Early scientists were rather vague about the meaning of the term force and it was Sir Isaac Newton (1642–1727) who first gave a clear definition of force and a coherent theory of the behaviour of bodies subject to forces. Newtonian mechanics formed the basis for the development of much of physics for nearly two hundred years.
More recently it has been realized that Newtonian mechanics is limited. It cannot give adequate explanations regarding the behaviour of particles moving with speeds comparable with that of light in a vacuum, nor can it account for the behaviour of atoms. Nevertheless, Newtonian mechanics still applies in a wide range of situations, and this is our topic of study in this module.
In Section 2 we introduce the idea of force and Newton’s laws of motion, which define force in terms of its action on bodies of a given mass. The three laws are discussed using vector notation. Section 3 introduces the most familiar forces – gravity, friction, and the tension in strings and springs, introducing Hooke’s law and its limitations. Section 4 deals with forces acting in conditions of mechanical equilibrium, where the resultant force on the system is zero. Section 5 describes various non-equilibrium situations, where the resultant force is not zero and there are non–zero accelerations present.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 6.1Module summary and the Subsection 6.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 6.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
A light, inextensible (i.e. it does not stretch) string ABCD has its ends A and D fixed to points on the same horizontal level. Two particles, one of mass 5 kg and another of mass M, are attached at points B and C, respectively. In the equilibrium state C lies below the level of B and AB, BC and CD are inclined at angles of 60°, 30° and 30° to the horizontal, respectively. Find the tension in each of the three sections of the string, and the value of M. (Take g = 9.81 m s−2).
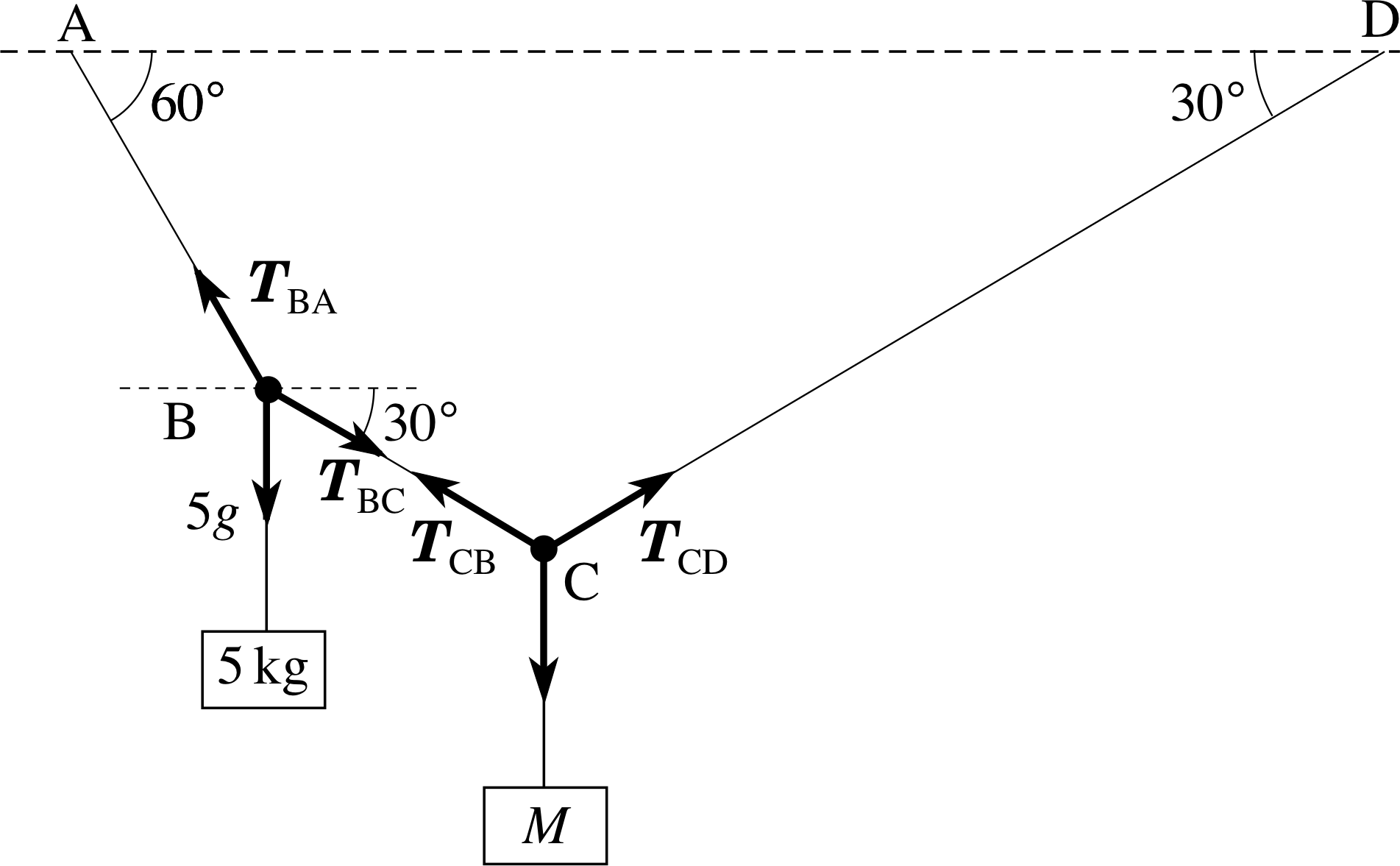
Figure 13 See Answer F1.
Answer F1
The solution is shown in Figure 13. Point B is in translational equilibrium due to the action of the three forces TBA, TBC and the weight (of magnitude 5g). Point C is in translational equilibrium due to the action of TCB, TCD and the unknown weight (of magnitude Mg). The equilibrium of the section of string BC requires that TBC = −TCB so TBC = TCB.
If we take components of the forces acting on B in the direction perpendicular to TBA, equilibrium requires:
TBC cos 60° = 5 kg × g cos 60°
i.e.TBC = 5 kg × g = 5 kg × 9.81 m s−1 = 49 N
If we take the horizontal components of the forces at B, we find
TBA cos 60° = TBC cos 30° = TBC sin 60°
soTBA = TBC tan 60° = 49 N tan 60° = 84.9 N
At C, since TCB and TCD are inclined equally to the horizontal, if we take the horizontal components we find:
TCB = TCD = TBC = 49 N
Taking vertical components at C, we find:
Mg = TCB cos 60° + TCD cos 60° = 2TBC cos 60°
soMg = 2 × 5 kg × g cos 60°
and finally M = 10 kg × cos 60° = 5 kg
Question F2
Two blocks, each with mass 4 kg, are connected by a light inextensible string which passes over a pulley attached to the top of a plane inclined at an angle θ to the horizontal. One block lies on the inclined plane while the other hangs vertically below the pulley. If the coefficient of sliding friction is 0.30 and tan θ = 0.75, find the acceleration of the blocks when they are released, and determine the magnitude of the tension in the string. If the mass of the hanging mass is changed so that when the complete system is set in motion in the same direction as before it continues to move with constant speed. Find the value of the hanging mass.
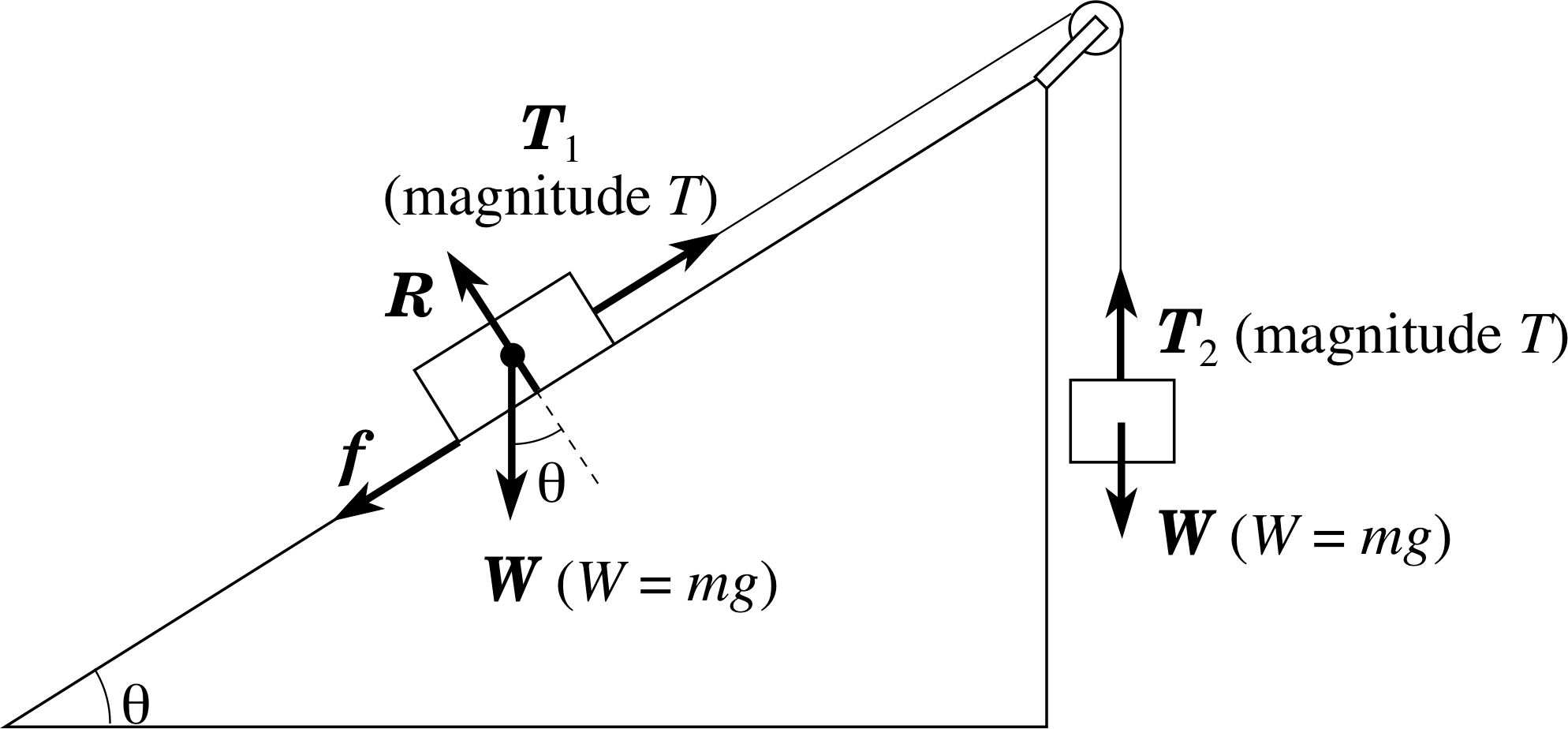
Figure 14 See Answer F2.
Answer F2
Since the blocks have equal mass (m, say), the block hanging vertically will accelerate downwards when the system is released. Since the string stays taut, the tension forces T1 and T2 acting on the blocks have the same magnitude T, and the acceleration for each block has the same magnitude, a, (but are in different directions, see Figure 14). To find the value of a we apply Newton’s second law to each block. For the block on the plane there is no acceleration perpendicular to the plane and so the magnitude of the normal reaction R is:
R = mg cos θ
The magnitude of the frictional force down the plane is f = μR = μmg cos θ. The resultant force component up the plane on this block (i.e. in the direction of motion) is:
T − f − mg sin θ = T − μmg cos θ − mg sinθ
so$a = \dfrac{T}{m} - \mu g \cos\theta - g \sin\theta$
$\phantom{a} = \dfrac{T}{m} - g(\mu \cos\theta + \sin\theta)$
For the other block, the vertically downward component of the resultant force is (mg − T) and so the acceleration of this block downwards (also a) is:
a = g − T/m
If we eliminate T/m between these two equations we find:
2a = g − g (μ cos θ + sin θ) = g (1 − μ cos θ − sin θ)
If we substitute values for g, μ and θ we have:
a = 9.81 m s−1 [1 − (0.30 × 0.80) − 0.60]/2 = 0.785 m s−2
andT = m (g − a) = 4 kg × (9.81 − 0.785) m s−1 = 36.1 N
For the blocks to move with constant speed in the same direction as given above, each block, once moving, must have no resultant force. If the mass of the hanging block is M:
Mg − T = 0
for the mass on the plane:
T − mg sin θ − μmg cos θ = 0
Eliminating T we find:
Mg − mg sin θ − μmg cos θ = 0 and M = m (sin θ + μ cos θ)
Substituting values for m, μ and θ we find
M = 4 [0.60 + (0.30 × 0.80)] kg = 3.36 kg
1.3 Ready to study?
Study comment To begin to study this module you will need to be familiar with the following terms: acceleration, Cartesian coordinate system, components_of_a_vectorcomponent (of a vector), displacement, distance, position vector, scalar, speed, vector, vector addition and velocity. Also, you will need to be familiar with the use of trigonometric functions. If you are uncertain about any of these terms then you can review them now by reference to the Glossary, which will also indicate where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
Distinguish between a scalar and a vector quantity. Which of the following are scalar and which are vector quantities:
time, length, velocity, displacement, speed and acceleration.
Answer R1
A scalar quantity has magnitude only, whereas a vector quantity has magnitude and direction.
Scalars: time, length and speed.
Vectors: velocity, displacement and acceleration.
(If you had difficulty with Question R1 consult scalar and vector in the Glossary.)
Question R2
Town A lies at the origin of a two–dimensional Cartesian coordinate system. Town B lies 8 miles from A in a direction which makes an angle of 30° with the positive y–axis, measured towards the positive x–axis. Express the position of B with respect to A in terms of (a) its position coordinate (x, y) and (b) the components sx and sy of its displacement vector s = (sx, sy).
Answer R2
x–component of B is (8 cos 60°) miles = 4 miles
y–component of B is (8 cos 30°) miles = 6.93 miles
The displacement vector s has components: (sx, sy) = (4 miles, 6.93 miles)
(If you had difficulty with Question R2, consult scalar and vector in the Glossary.)
Question R3
A particle travels a distance of 50 m along the x–axis of a coordinate system and then reverses its direction and travels back a distance of 10 m. If the whole process takes 2 s to complete, calculate the average speed of the motion and the magnitude of the average velocity.
Answer R3
Average speed = total distance/total time
Thereforeυav = (50 m + 10 m)/2 s = 30 m s−1
Average velocity = displacement/total time
Therefore the magnitude of the average velocity is 40 m/2 s = 20 m s−2.
(Consult speed, distance, velocity and displacement in the Glossary for further details.)
Question R4
At a certain time the velocity υ1 of a particle is 3 m s−1 due east. The velocity υ2 10 s later is 4 m s−1 due south. Find the magnitude and direction of the average acceleration over this time interval.
Answer R4
Average acceleration = (υ2 − υ1)/time interval. If we add vector (−υ1) to vector υ2, the resultant (υ2 − υ1) is found to be at an acute angle θ west of south, such that:
tan θ = 3/44 i.e. θ = 36.9°
The magnitude of (υ2 − υ1) is easily obtained, since a 3, 4, 5 triangle is formed, i.e. the magnitude is 5 m s−1. Therefore the magnitude of the average acceleration is 5 m s−2/10 s = 0.5 m s−2.
(Consult acceleration and vector addition in the Glossary for further details.)
2 Newton’s laws of motion
In everyday use the term force equates to a push or a pull; we will be able to be more precise than this in a while, but for the moment this description is sufficient. Kinematics is the study of motion. Dynamics is the study of how forces influence motion. Everyday experience suggests that a push or pull must be continually applied to an object to keep it moving at constant speed. If we stop pushing an object along a flat surface it soon slows down and stops, but there is no simple rule which tells us how long it will take to stop. The surface involved makes a great deal of difference. The stopping time on a carpet is very different to that on ice. If we feel these different surfaces with our fingers then the reason becomes obvious – the two surfaces offer very different resistances to the motion of anything sliding over them. We are all familiar with this resistance and generally call it friction. i Friction operates whenever two objects (not necessarily both solid) in contact are in relative motion or if an attempt is made to cause relative motion. Friction occurs also in other circumstances but it is often given other names. For example, it accounts for the viscosity between a solid and liquid, and the air resistance encountered by a body moving through the atmosphere. We will say a little more about frictional forces between solid surfaces in Subsection 3.3.
Whatever the nature of these frictional forces, they all have a direction which opposes the relative motion that causes them and, unless a continuous ‘push’ is provided, they slow and eventually stop this motion. But what would happen in the absence of friction; how long would it take for a moving object to stop under such conditions? We are all familiar with the almost frictionless motion of a spacecraft travelling through space. The rocket engines are not required to sustain the flight in space, but only to change the motion in some way – to increase or decrease speed, or to change direction. In normal uniform flight, the engines are not needed. Newton’s insight was to realize that forces change rather than sustain motion – and he saw this long before space flights made it obvious. i For our part, we still find this idea a little strange because it does appear to be in conflict with our friction–dominated everyday lives. Newton realized that a moving object will not stop of its own accord, but that it will carry on moving in a straight line unless it is interfered with by a force acting on it, e.g. friction, or by hitting something.
These ideas may be made more quantitative by using Newton’s laws of motion, which explain how bodies move and interact with one another. i Before we introduce these laws we will remind you of some basic terms and definitions, developed elsewhere in FLAP. These are collected together in Table 1 for reference.
| Quantity (nature) | Definition | |
|---|---|---|
| position (vector) of a point | A vector drawn from the origin of a coordinate system to the point |
r |
| displacement (vector) from A to B | The difference in the position vectors of A and B | sAB = rB − rA |
| distance (positive scalar) from A to B | The magnitude of the displacement from A to B | sAB = | sAB | = | rB − rA | |
| velocity (vector) | The rate of change of the position vector | $\upsilon = \dfrac{d\boldsymbol{r}}{dt}$ |
| speed (positive scalar) | The magnitude of the velocity, the rate at which distance is covered |
$\upsilon = \lvert\,\boldsymbol{\upsilon}\,\rvert = \left \lvert\,\dfrac{d\boldsymbol{r}}{dt}\,\right\rvert$ |
| relative velocity (vector) of B relative to A | The rate of change of the displacement from A to B | $\boldsymbol{\upsilon}_{\rm AB} = \dfrac{d\boldsymbol {s}_{\rm AB}}{dt}$ |
| relative speed (positive scalar) of B relative to A | The magnitude of the relative velocity | $\upsilon_{\rm AB} = \lvert\,{\boldsymbol\upsilon}_{\rm AB}\,\rvert = \dfrac{d{\boldsymbol s}_{\rm AB}}{dt}$ |
| acceleration (vector) | The rate of change of velocity | ${\boldsymbol a} = \dfrac{d{\boldsymbol \upsilon}}{dt}$ |
| uniform motion | Motion at constant velocity, that is with constant speed along a fixed direction. Uniform motion involves no acceleration |
2.1 Newton’s first law of motion; condition for uniform motion
We can now state more formally the situation just described.
Newton’s first law of motion
A body of constant mass remains at rest or in a state of uniform motion unless it is acted on by an unbalanced force.i
The word unbalanced has been added in this statement because it is quite possible for a body to be acted on by two or more forces which cancel one another out. For example, if we apply a sufficient force to our sliding object so that this force is equal in magnitude but opposite in direction to the frictional force acting, the combination of these two forces produces no net unbalanced force and the object continues to move with a constant velocity. We say then that the forces acting on the object are balanced forces. We now have a physical interpretation of the word force. A force is something which changes the state of motion of a body. However, only an unbalanced or resultant force can do this. If there is no resultant force then the body moves with uniform motion.
Note that if no resultant force is acting on an object of constant mass then it is the velocity of the object which must remain constant and not merely its speed. This means that neither the magnitude nor the direction of the velocity changes. Thus the body moves with constant speed along a straight line unless it is acted on by a resultant force. This property of a body in persisting in its state of motion, or of resisting any change of its motion is called the inertia of the body. Sometimes Newton’s first law of motion, is called the law of inertia.
Do not be misled into thinking that Newton’s first law is always valid for any observer. In some situations an object is observed to accelerate, even when there is no resultant force acting on it! We can understand this surprising statement if we consider how an observer measures the motion of an object. The position of the object is measured in a coordinate system which is fixed with respect to the observer (usually in terms of the three mutually–perpendicular axes of a Cartesian coordinate system). In addition there must be some well defined procedure for determining the time at which the object occupies any particular position. Such a system for measuring positions and times (and hence velocity and acceleration) is called the observer’s frame of reference. The key point to appreciate is that the same sequence of events may look very different to two different observers with their different frames of reference. In particular, Newton’s first law is not valid in all frames of reference. For example, consider a book on a frictionless table in a train. When the train brakes, the book slides off the table. An observer on the platform will interpret this event as the book continuing to move with its initial velocity, while the table slows down – since it is attached to the train, which is braking due to the force applied at the track. There is no resultant force on the book and its uniform motion is consistent with Newton’s first law.
However, to an observer sitting at the table on the train the book accelerates off the table, for no apparent reason and with no obvious forces acting on it. This observer has two options. One option is to accept that Newton’s first law is not valid in his or her frame of reference and the other option is to invent some fictitious force on the book to account for the observation. The first option expresses a qualified belief in Newton’s first law in some frames of reference while the second expresses an unqualified belief in Newton’s first law in any frame of reference at the cost of introducing a force for which no physical basis can be given. The second option is attractive since the observer on the braking train will feel the same tendency to accelerate relative to the train as the book, but physicists generally accept the first option. Thus, Newton’s first law may be used to identify a particular set of frames of reference – those in which the law is true.
A frame of reference in which Newton’s first law is obeyed is called an inertial frame of reference. A frame of reference in which the first law is not obeyed is called a non–inertial frame of reference. It is apparent that the distinguishing feature between these two is acceleration.
Any accelerated frame of reference must be a non–inertial frame of reference; all inertial frames of reference must be non–accelerated frames.
Note In applying Newton’s laws of motion always remember to choose an inertial frame of reference. Usually it is obvious which these are, but in some problems, it is less obvious.
2.2 Newton’s second law of motion; force and mass
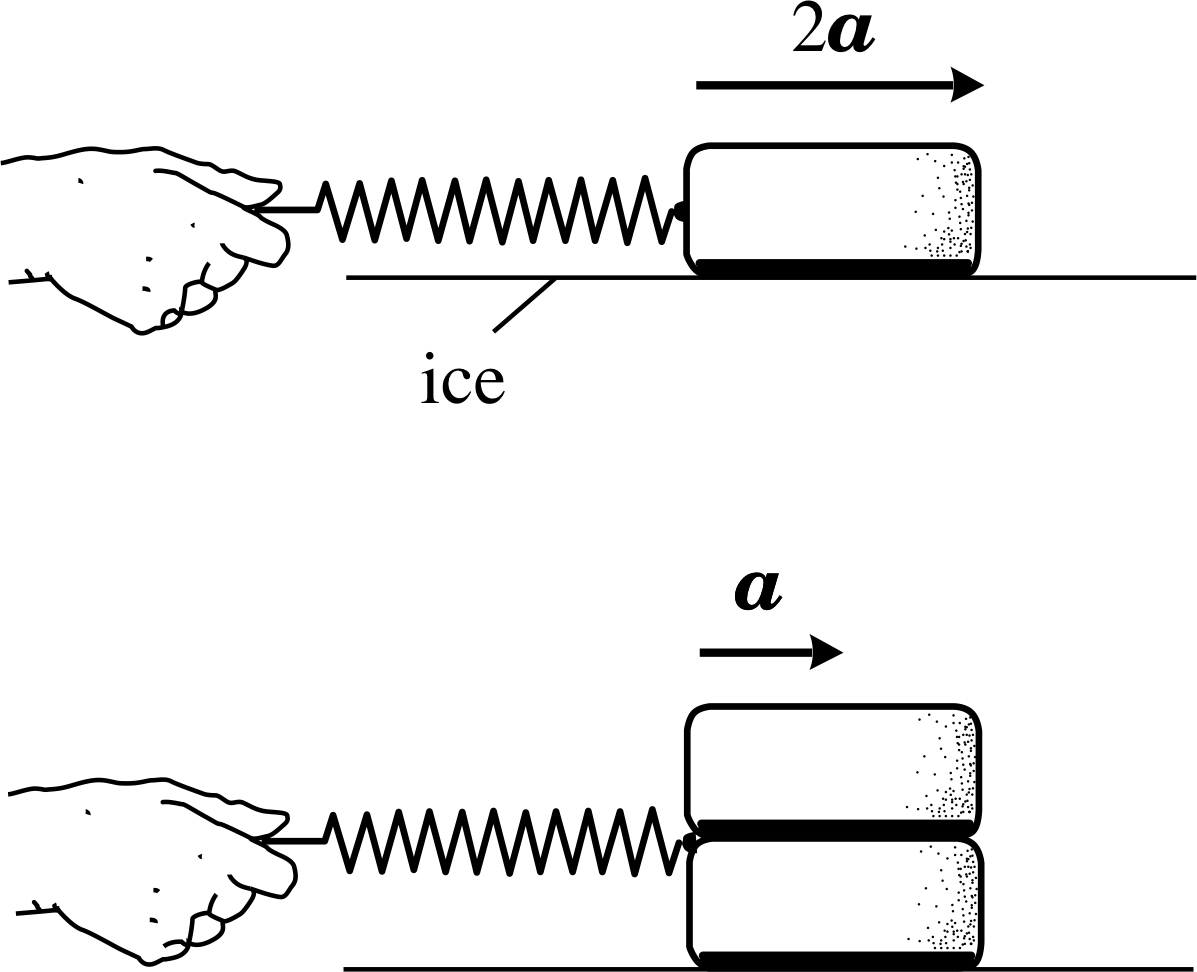
Figure 1 A spring compressed to a certain length exerts the same force on a single puck and a double puck. The acceleration of the single puck is twice that of the double puck.
Suppose that we have an ice–hockey puck on a smooth sheet of ice – which can be treated as a frictionless surface. The puck needs a force to start it moving and another force, acting in the opposite direction, to stop it. Between these two events it moves freely with uniform velocity, subject to no resultant force. If you measure the size of the force needed to produce a given change of velocity in a given time you will find that it depends on the size of the puck. A larger force is needed if two pucks are joined together. In other words, the double puck has a greater inertia than the single puck. To see just how these two inertias are related we must observe the effect of the same force on each of them.
✦ Since we don’t yet know how to measure forces, how could we do this?
✧ One way would be to push each system, using a spring compressed by the same amount in each case, as shown in Figure 4.
When we do the experiment of applying the same force i to the double puck and the single puck we find that the magnitude of the acceleration of the single puck is twice that of the double puck:
i.e.$\dfrac{\text{magnitude of the acceleration of the single puck}}{\text{magnitude of the acceleration of the double puck}} = \dfrac21$
This observation can be given the reasonable interpretation that the inertia of the double puck (its resistance to acceleration) is twice that of the single puck. The property of an object which characterizes its inertia is called its inertial mass or simply its mass, and so we say that the mass of the double puck is twice that of the single puck.
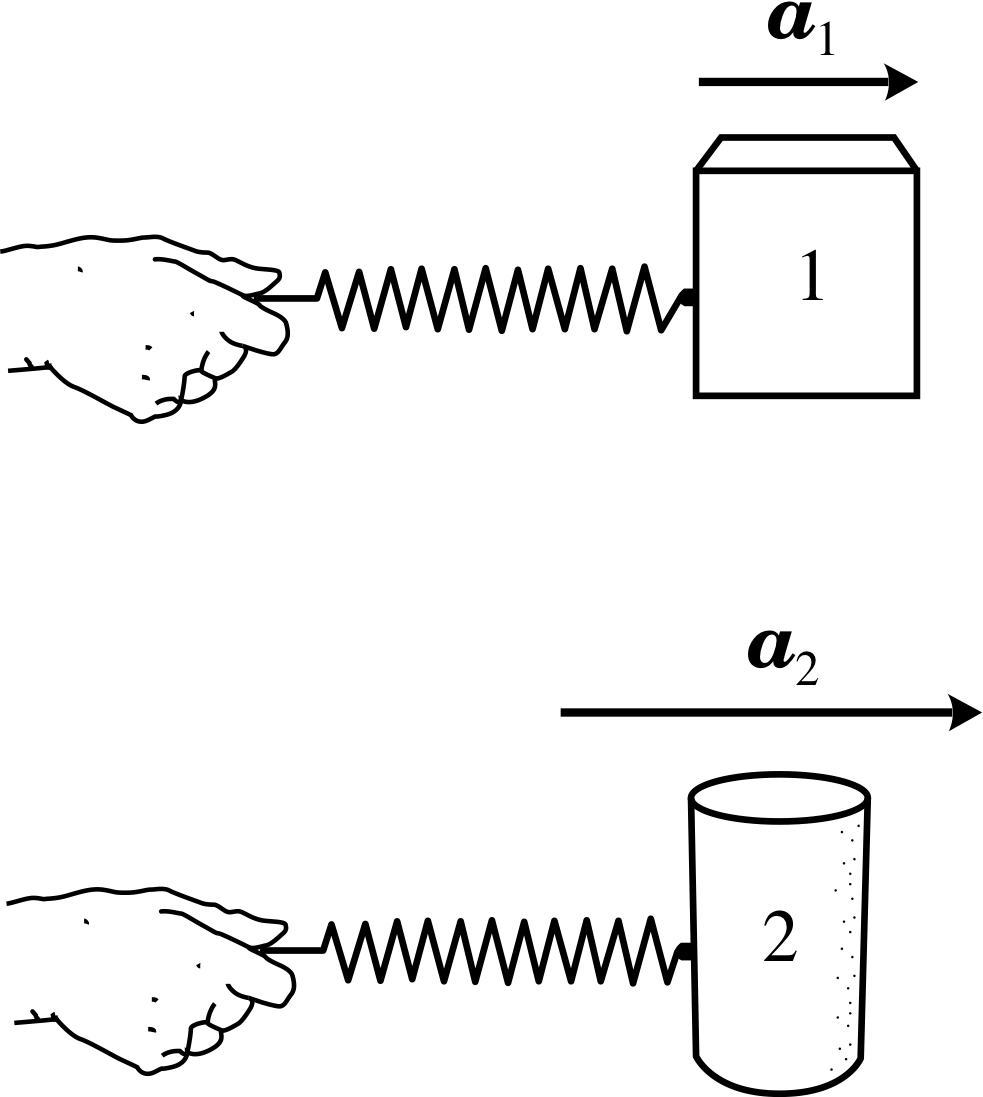
Figure 2 To compare the masses of two objects, we push them both with the same force (provided by a spring whose compression is kept constant) and measure their accelerations.
In the general case we can compare two masses by comparing the magnitudes of their accelerations when subject to any given force. Such an experiment is shown in Figure 2. In this experiment, object 1 has an acceleration of magnitude a1, and object 2 has an acceleration of magnitude a2.
The ratio of the masses m1 and m2 of the objects is defined by:
$\dfrac{m_1}{m_2} = {a_1}{a_2}$(1)
i.e.m1a1 = m2a2
It then makes sense to define the common force of magnitude F acting in this experiment as:
$F = ma$(2)
However, Equation 1 defines only the ratio of two masses and Equation 2 links the two quantities, force and mass, without either being measurable separately since we have no units for either. To make further progress and to assign a numerical value to the mass of any object or a force acting, we need a standard of mass. In the SI system of units this standard is the kilogram (kg).
You may wonder here why a standard of mass is adopted and force is defined in terms of mass and acceleration, rather than the other way around. The explanation is due to convenience and precision. It is very much easier to take a lump of matter as a standard mass and to make copies of it, rather than to use standard compressed springs as a unit of force. Masses can be compared to high precision by weighing, as we will see in a moment, but the force of a compressed spring is much more elusive – its effects can only be observed by releasing it!
Also, compressed springs do not maintain their potency indefinitely, whereas the mass of an object at rest i does not change with time, unless it exchanges matter with its surroundings.
Note that mass is a positive scalar quantity and that masses add in a simple arithmetic manner. For situations outside the realms of nuclear physics and where speeds are very much less than the speed of light, the principle of conservation of mass applies to a very good approximation: i
If an object does not exchange any matter with its surroundings, its mass at rest remains constant with time.
We are now in a position to give Newton’s second law of motion, which for a body of constant mass m, may be stated as follows:
Newton’s second law of motion
An unbalanced force acting on a body will accelerate the body. The acceleration produced is in the same direction as the unbalanced force and the magnitude of the acceleration is equal to the magnitude of the unbalanced force divided by the body’s mass.
If the x–direction is defined as the direction in which the unbalanced force acts, then Newton’s second law of motion can be written as:
Fx = max(3) i
where Fx and ax are the x–components of the force and the acceleration it produces.
Whereas the first law gives us an interpretation of the meaning of force, the second law gives the means of quantifying force. Note that the second law, like the first law, is valid only in inertial frames of reference.
Using Equation 3 we may determine the units of force. Clearly the SI unit of force is that of mass × acceleration, i.e. kg m s−2. This unit is given the name newton and is represented by the symbol N. Thus:
1 newton = 1 N = 1 kg m s−2
Question T1
If a resultant force of 5 N magnitude is applied to an initially stationary body and produces an acceleration of magnitude 0.5 m s−2, what is the mass of the body?
Answer T1
Using Fx = max(Equation 3), we obtain m = Fx /ax = 5 N/0.5 m s−1 = 10 kg.
Question T2
A car of mass 800 kg travels on a level road with an acceleration of magnitude 0.75 m s−2, caused by a driving force of 900 N and an opposing resistive force of magnitude FR. Determine FR.
Answer T2
If m is the mass of the car and FD is the driving force, then applying Newton’s second law we find
ma = FD − FR
therefore
FR = FD − ma = 900 Ν − (800 kg × 0.75 m s−1) = 300 N
2.3 Newton’s third law of motion
When you push against a wall with your hand you feel a force exerted by the wall in the opposite direction. The greater your push, the greater the force with which the wall pushes back. In fact, these two forces are equal in magnitude but opposite in direction. This illustrates Newton’s third law of motion, which may be stated as:
Newton’s third law of motion
When two bodies interact with each other, each body exerts a force on the other. These two forces are equal in magnitude but opposite in direction.
The implication of this law is that forces always occur in pairs; a single force cannot exist. Such a pair of opposed forces is called a third law pair. Thus, whenever you encounter a force you should always ask yourself, ‘What is the second force predicted by Newton’s third law of motion?’ Of course, when you have to predict the motion of an object it is only the forces on this object which need be considered, not the forces this object exerts on another object. i
✦ What, according to Newton’s third law, is the pair of forces involved when a rocket is launched vertically upwards?
✧ The rocket exerts a downward force on the combustion products ejected from the rocket, and the combustion products exert a force on the rocket. These forces are equal in magnitude and are the third law pair of forces. When considering the rocket, it is the upward force that is responsible for the rocket’s upward acceleration; we do not need to consider the third law pair (as it acts on a different body).
A word of caution is necessary here. If two forces happen to be equal in magnitude but oppositely directed they do not necessarily form a Newton’s third law pair. The pair of forces must satisfy the conditions incorporated in the third law in order to be a third law pair. The crucial condition is that the two forces must be exerted on two different bodies; not on the same body. Thus for example, if two elephants push with equal force in opposite directions on a tree trunk, nothing happens, except for a minor amount of squashing of the tree. Here we have forces of equal magnitude, oppositely directed, but they do not form a third law pair, because the forces are exerted on the same body, i.e. the tree.
✦ Can you identify the third law pairs in the elephant example?
✧ Elephant 1 pushes on the tree and the tree pushes back on elephant 1 with a force equal in magnitude but opposite in direction. The same reasoning applies for the force exerted by elephant 2. Hence we have two third law pairs of forces in this example.
The fact that the two forces exerted by the two elephants on the tree do not comprise a third law pair is clear if one elephant pushes harder than the other, because the forces are then not equal in magnitude. However, we can still identify the true third law pairs, as indicated in the question.
A common example of a third law pair occurs where an object is at rest on a horizontal surface, we know from Newton’s first law that the forces acting on it must balance. This means that there must be an upward force which exactly counteracts the weight of the object. This upward force is the force that the surface exerts on the object and is known as the reaction force R, or sometimes, the normal force N (because the force is normal to the surface of contact). i As its name implies, it is part of an important third law pair, but the other part of the pair cannot be the weight, since that acts on the same body as the reaction. Rather, the reaction is paired with the force that the body exerts on the surface.
Question T3
A lazy person with a slight knowledge of physics is asked to push a heavy refrigerator to a new position in a kitchen. He objects, answering as follows: ‘If I push on the refrigerator it will push back on me with a force equal in magnitude to mine, so I can never start the refrigerator moving’. What is wrong with this excuse?
Answer T3
To move the refrigerator the force applied to it must be sufficient to overcome the friction force exerted by the floor on the refrigerator. The forces referred to by the lazy person act on different bodies and cannot, therefore, keep the given body (refrigerator) in equilibrium.
Question T4
Another lazy person, with slightly more knowledge of physics, is asked to hang up a picture. She claims that it is impossible to knock a nail into the wall since the force on the nail from the hammer will be matched by an equal but opposite reaction force from the wall. What is wrong with this statement?
Answer T4
Consider all the forces on the hammer and the nail.
On the moving hammer, the only force acting is the force from the nail at impact; this force is opposite to the hammer’s motion and eventually stops the hammer, but not instantaneously, since the hammer head has mass and the force is not infinitely large (i.e. Newton’s second law in action).
On the nail there are two forces acting; there is the force applied by the hammer, which is the third law pair force to the force on the hammer, and there is a force applied by the wall, which is the third law pair force to the force which the nail applies on the wall. So, the two forces acting on the nail are not themselves a third law pair and they can be unequal. Here they must be unequal and the resulting force on the nail causes it to accelerate into the wall. Finally, the hammer and nail together are brought to rest by the reaction and frictional forces at the wall. The reason for the point on the nail is to limit the region of interaction and so limit the size of these forces at the wall – allowing a longer time for the nail to be brought to rest.
The lesson to learn from this is that we must be very careful to identify third law pair forces and also to remember that an accelerating object has a resultant force on it.
Newton’s laws of motion apply for any type of force, and form the basis of Newtonian mechanics or classical mechanics, the branch of physics in which the motion of objects is related the forces acting on them by means of Newton’s laws.
2.4 Vector expressions of Newton’s laws of motion
So far we have described forces and accelerations as acting along the x–axis, with all motion taking place along this same axis. Such motion is known as linear motion, since the position of the object can be described in terms of a single coordinate, say x. This is not the general case, as motion is often in three–dimensional space, with the position of the object described in terms of three position coordinates, x, y and z. In general, the direction of motion may be quite different from the direction of the applied force and the acceleration it produces. To deal with this situation we need to use a vector representation of Newton’s laws, with forces and accelerations represented as vectors or as components of vectors.
Equation 3, Fx = max, is an example of a component equation, where the x–component of the acceleration results from the x–component of the force. Similar relationships exist between the y– and z–components of force and acceleration. In general, both the unbalanced force and the acceleration have three components, so we can write:
F = (Fx, Fy, Fz) and a = (ax, ay, az)
The unbalanced force F itself may be derived from the combined effects of several applied forces. As for other vector quantities, forces add vectorially and if we have more than one force acting on a single body then the resultant force is the vector sum of all the forces acting. We write this as $\displaystyle \sum_{i=1}^N \boldsymbol{F}_i$. i
Newton’s first law corresponds to the case where F is the zero vector 0. We can write this as
$\displaystyle \sum_{i=1}^N \boldsymbol{F}_i = \boldsymbol{F} = \boldsymbol 0$(4)
For a body of constant mass, Newton’s second law associates this condition with zero acceleration:
a = 0(5)
and therefore uniform velocity
u = (ux, uy, uz) (a constant vector)(6)
In component form in three dimensions, Equations 4 and 5
$\displaystyle \sum_{i=1}^N \boldsymbol{F}_i = \boldsymbol{F} = \boldsymbol 0$(Eqn 4)
a = 0(Eqn 5)
can be written as:
Newton’s first law:
IfFx = 0, Fy = 0 and Fz = 0(7)
thenax = 0, ay = 0 and az = 0(8)
since a vector cannot be zero unless each of its separate components is zero. Equations 4 and 5, (or 7 and 8) express Newton’s first law in vector (or component) form.
We can most usefully express Newton’s second law (incorporating Equation 3)
Fx = max(Eqn 3)
in terms of the corresponding components on either side of the equation:
Newton’s second law:
Fx = max, Fy = may, Fz = maz(9) i
soF = (Fx, Fy, Fz) = (max, may, maz) = m (ax, ay, az)
i.e.F = ma
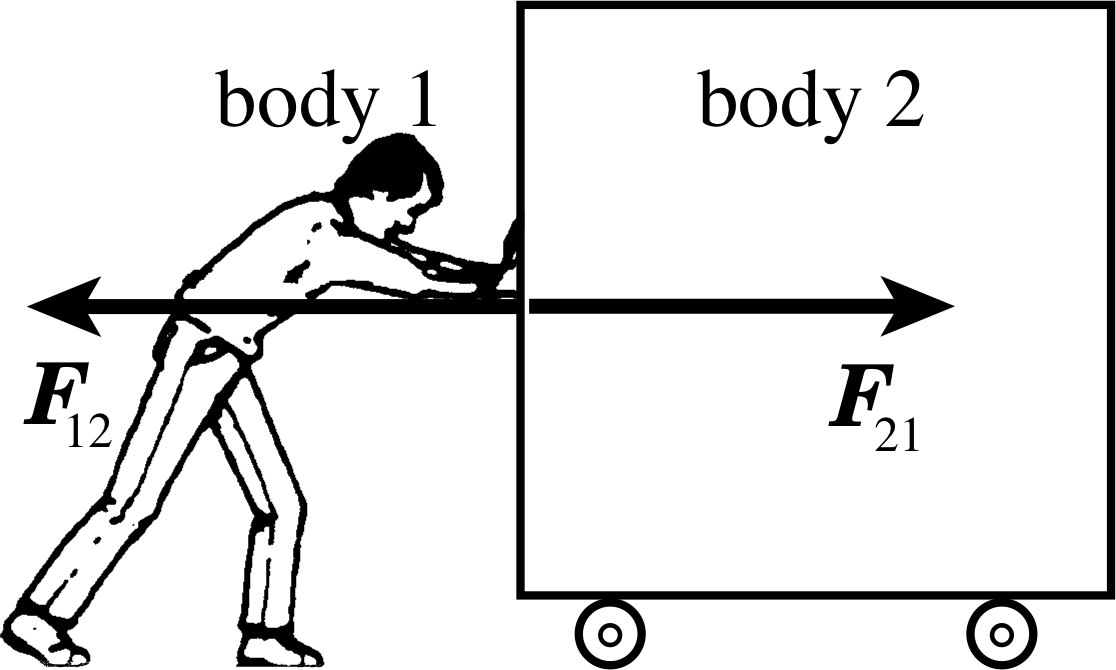
Figure 3 Bodies 1 and 2 interact with each other. If body 1 exerts a force F21 on body 2, then body 2 must exert a force F12 on body 1. The two forces are of equal magnitude, but they act in opposite directions.
Equation 9 expresses the basic simplifying idea that each component acts independently of the other components. Using this idea, a single problem in three dimensions becomes three simple problems each in one dimension; three–dimensional problems are no more difficult than one–dimensional ones; they just take longer to work out.
For the special case of linear motion along the x–axis, Equation 9 simplifies to:
ay = az = 0 and Fy = Fz = 0
withFx = max(Eqn 3)
as the expression of Newton’s second law for motion along a straight line.
Newton’s third law also may be expressed vectorially. Let F12 be the force exerted on body 1 by body 2 and F21 be that exerted on body 2 by body 1. Then Newton’s third law is summarized by the equation:
F12 = −F21(10)
This is illustrated in Figure 3.
2.5 Newton’s laws and extended bodies
Throughout our discussion of Newton’s laws we have repeatedly referred to the behaviour of ‘a body’. This term has been carefully chosen to cover two classes of object: particles which may be treated as structureless and small enough to be located at a point, and extended bodies which occupy some finite volume and may have an internal structure.
The application of Newton’s laws to particles is clear and unambiguous. If we say that a particle accelerates or that a particle moves with constant velocity there is no room for doubt about what is being said provided we know the frame of reference in which positions and times are being measured. The same is not true when dealing with extended bodies: more precision is required. The effect of a given force on an extended body depends on the part of the body to which the force is applied. For example, if you lay a book on a smooth table, put your finger against the middle of the book’s spine and apply a force at right angles to the spine the whole book will slide across the table without rotating. (This kind of motion, in which all parts of the body move along parallel linear paths is called translation.) On the other hand, if you apply the same force to a point near the bottom of the book’s spine the book as a whole will still move, but it will rotate as it does so. In this case a point near the centre of the book will undergo translation while the rest of the book rotates around that point.
The behaviour of the book is indicative of the behaviour of extended bodies in general. When forces are applied to an extended body there will always be a point called the centre of mass, that behaves as though it were a particle with a mass equal to the total mass of the body. It is the behaviour of this point that is most easily understood in terms of Newton’s laws. (The application of Newton’s laws to other parts of the body is still justified, but it is complicated by the internal forces that one part of the body may exert on other parts; in the case of the centre of mass such internal forces always cancel out.) In the rest of this module whenever we refer to the velocity or acceleration of an extended body it is always the velocity or acceleration of the centre of mass that is meant.
It is not possible in the space available to give a precise mathematical definition of the centre of mass from which you could locate it for an arbitrary body. (That, together with the rotational effect of forces is dealt with elsewhere in FLAP.) Stated informally, however, the centre of mass is the ‘average’ position of the mass of a body. Any body, or indeed any collection of bodies, has one unique centre of mass at any time. If it is a rigid body in which the parts have no relative motion the centre of mass will have a fixed location. If the body is flexible, like a human being, or has a changing mass like a rocket burning fuel, the location of the centre of mass will generally change with time. In either case it will still be a unique point at any particular time.
In simple cases the uniqueness of the centre of mass may be used to determine its position. For instance the centre of mass of a uniform sphere is at its geometric centre. This must be so; no matter how you rotate the sphere the mass distribution is unchanged so the centre of mass must also be unchanged, but the only point in a sphere that is unaffected by arbitrary rotations is the geometric centre. Hence the geometric centre is also the centre of mass. A similar argument applies to a sphere in which the density depends only on the distance from the centre.
✦ A bicycle wheel rotates freely on an axle. Where is the centre of mass of the wheel?
✧ The centre of mass is at the geometric centre of the wheel, a point which is not actually ‘inside’ the matter of the wheel at all. There is no reason to expect that the centre of mass of a body is within the material of the body.
2.6 Summary of Section 2
Newton’s three laws of motion cannot be proved from more basic equations but are justified by their consistency with experimental observation. In effect, the first law describes force – it is that which causes a change in motion (i.e. an acceleration) of an object of constant mass. The second law introduces mass and enables force to be quantified by relating it to the mass of an object and the acceleration produced (using F = ma). The third law shows us that to every force acting there is a reaction of equal magnitude acting in the opposite direction on another object. Newton’s laws of motion may be expressed in vector form or in terms of components.
3 Three familiar forces – gravity, friction and tension
3.1 Terrestrial gravity; weight
There is no force more familiar to us than the force of gravity; whenever we trip up, it is there waiting for us. The effect of terrestrial gravity on any small body near the surface of the Earth is equivalent to that of a single downward force acting through the centre of mass of the body. This equivalent single force is called the weight of the body.
A body falling freely near the Earth’s surface, without being impeded by air resistance, will accelerate downwards with the acceleration due to gravity of magnitude g. The value of g varies slightly from place to place on Earth, from about 9.78 to 9.82 m s−2, but it is generally taken to be 9.81 m s−2. i However, the value of g is the same for all bodies at a given place; it does not depend on the nature or mass of the body involved.
This is not always obvious in everyday life. A cricket ball and a penny will take the same time to hit the floor if they are dropped from the same height, but if we replace the cricket ball by a feather or a scrap of paper, then we find that the penny reaches the floor much earlier. We explain this by saying that the feather (or paper) is affected much more by air resistance than is the penny, and we can confirm this explanation by repeating the experiment in an enclosure from which all the air has been pumped out; then we find that the two objects behave in the same way. This experiment was done rather dramatically by the Apollo 11 astronauts on the surface of the Moon; a hammer and a feather were seen to fall at the same rate when unencumbered by an atmosphere.
If we apply Newton’s second law to a freely falling body of mass m, knowing that the acceleration downwards has a magnitude g, we see that the weight W, acting vertically downwards, has a magnitude W given by:
W = mg(11)
this relation is sometimes called the law of terrestrial gravitation. It shows that in any region where g is constant, the weight of a body is directly proportional to its mass.
Weight is not the same as mass, although the two words are used interchangeably in ordinary speech. Weight is a force, and so is a vector quantity; it should be measured in newtons. Mass is a scalar quantity, a measure of inertia, and is usually measured (by physicists, at least) in kilograms. As we have just seen, the two quantities are usually directly proportional to one another, and it is for this reason that they are not distinguished by the non–scientist – ask most non–scientists what is the weight of a 1 kg bag of sugar and watch their puzzled expressions – before they finally answer ‘about two and a quarter pounds’! i
✦ What then is the weight of a 1 kg bag of sugar?
✧ The magnitude is W = mg = 1 kg × 9.8 m s−2 = 9.8 N, so the weight (force) is about 10 N, vertically downwards (i.e. do not forget the direction when asked to specify a vector quantity).
Question T5
Estimate the magnitude of the weight of the following objects:
an apple, a large car, a litre of water, a jar of jam, a fully laden juggernaut lorry.
Answer T5
Let us first estimate the masses of the given objects: A medium sized apple, 0.1 kg; a large car, 1000 kg; a litre of water, 1 kg; a pound jar of jam (including jar), 0.5 kg; a fully laden juggernaut, 40 × 102 kg. To obtain the weights of these objects we simply multiply the masses by 9.8 m s−1, and round the figures sensibly, since the masses are mainly rough estimates. Hence we obtain the following estimates for the weights:
apple, 1 N; car, 102 N; litre of water, 10 N; jar of jam, 5 N; juggernaut, 4 × 102 N.
✦ If we take a body of mass m to the Moon, do the values of the mass and the weight change?
✧ The mass of the body is exactly the same on the Moon as on Earth, since mass is a measure of the inertia of the body, and is determined by the amount of matter in the body. However, since the acceleration due to gravity on the Moon is about one–sixth of that on Earth, the magnitude of the weight (W = mg) of the body on the Moon would also be about one–sixth of that on Earth.
Question T6
A stone weighed on the Moon has the same weight as another stone weighed on Earth. Which stone requires the larger force to produce a given acceleration – and hence, which would hurt more, if kicked?
Answer T6
For the weights to be equal the mass of the stone on the Moon needs to be six times larger than that of the other stone on the Earth. Hence the Moon stone would require the larger force to accelerate it and would therefore hurt more if kicked.
Many instruments which claim to measure mass and which are calibrated in mass units actually measure force not mass. For instance, all instruments which rely on compression or extension of springs, such as bathroom scales, really measure force (i.e. weight), and should really be calibrated in units of force. In effect, they all use Equation 11,
W = mg(Eqn 11)
to convert weight into mass using a particular value of g. The small variation in g from place to place on Earth is insignificant for most purposes.
✦ If you took your bathroom scales to the Moon, how would its reading differ from that back on Earth?
✧ Your weight would be only one–sixth that on Earth and so the reading would be only one–sixth that on Earth. Since the scale claims (incorrectly) to measure mass, your mass would appear to have gone down spectacularly! Of course, your mass is actually unchanged.
To make a convenient measurement of mass we often use an instrument to compare the weight of the unknown mass with the weight of some known masses. A typical example of such an instrument is the traditional chemical balance, with scale pans hanging from the ends of a beam which is pivoted at its midpoint. The unknown mass is placed on one pan, and known masses are placed on the other until a balance is achieved. In this state the weights of the contents of the two scale pans must be equal, and since g has the same value at both scale pans, Equation 11 implies that the two masses are equal. i
✦ With such a chemical balance, would we measure masses correctly (a) on the Moon and (b) in space, remote from Earth (or other large bodies)?
✧ (a) Yes, because the weights of both the unknown mass and the known masses would be changed by the same factor (about one-sixth).
(b) No, because in weightless conditions we could place any masses in the pans and the balance would be unaltered.
Question T7
A person stands on bathroom scales in a lift. Explain quantitatively what happens to the reading on the scales when the lift: (a) moves upwards at constant speed; (b) accelerates upwards with an acceleration of ax; (c) accelerates downwards with ax < g and also with ax ≥ g. [Hint: Think about the frame of reference.]
Answer T7
(a) Since the lift moves at constant speed there is no acceleration and this is an inertial frame and the reading remains the same.
(b) If the person is accelerated upwards (positive x) there must be a resultant force upward. This means that the reaction force of the scales on the person must exceed the weight of the person. Applying Newton’s second law:
max = R − mg i.e. R = mg + max = m (g + ax)
Now R is the Newton’s third law pair to the force which the person applies to the scales and this determines its reading. The magnitude of the person’s weight in this non–inertial frame has increased from W = mg to W ′ = m (g + ax).
(c) The argument follows the same line as in (b) except that now the person has a resultant force downwards (positive x). Newton’s second law gives:
max = R − mg i.e. R = mg − max = m (g − ax)
The magnitude of the person’s weight in this non–inertial frame has decreased from W = mg to W ′ = m (g − ax). If ax< g then R is still finite, but when ax = g, R becomes zero and the person becomes weightless in this frame. If ax> g, then, in the lift frame of reference, the person accelerates upwards with an acceleration of magnitude (ax − g), hitting the ceiling!
We have glossed over an interesting subtle point in linking masses to weights. When we calculated the free fall acceleration of a mass m we had to divide the force acting (the weight) by the mass, in accordance with Newton’s second law – that is a = W/m. In this expression the m is the property of the body which determines its inertia, its reluctance to accelerate under any force; strictly speaking this is called the inertial mass. On the other hand, when we write W = mg, the m refers to the property of the body which determines the gravitational attraction to the Earth; there is no obvious reason why the gravitational force should have anything to do with inertia and we ought to have used two different ‘masses’ for the body.
The magnitude of a should be
$a = \dfrac{W}{m_1} = \dfrac{m_{\rm G}g}{m_1} = \dfrac{m_{\rm G}}{m_1}g$
where mI is the inertial mass and mG is the gravitational mass, defined by W = mGg. The consequence of this is that only if mI and mG are equal do all bodies accelerate at g. Experiments confirm this fact and so it appears that these two masses are equal, without any obvious theoretical justification.
3.2 Universal gravity

Figure 4 A Newtonian brainwave.
According to legend, Newton was sitting in his garden, pondering the motion of the planets, when an apple fell on his head (Figure 4). He realized that the forces between the Sun and the Earth and between the apple and the Earth are all due to the same phenomenon – gravity.
He suggested that any two objects should attract each other with a force due to gravity and that this force should increase in proportion to the masses of each of the objects and should decrease in some way as the distance beween them increases. By considering the motion of the Moon around the Earth, Newton deduced that the force must decrease inversely as the square of the distance between the masses.
He formulated his law of universal gravitation, i which gives the magnitude of the attractive force between two particles of masses m1 and m2, when they are separated by a distance r:
$F_{\rm grav} = \dfrac{Gm_1m_2}{r^2}$(12)
The constant G is called the universal gravitational constant and its value is 6.67 × 10−11 N m2 kg−2.
Equation 12 may also be used to predict the attractive force between two extended bodies of finite size. In essence, this is achieved by treating each body as a collection of particles and working out the total force that all the particles in one of the bodies exerts on each of the particles in the other body. i This procedure is generally very complicated, but it can lead to useful results if the bodies concerned are sufficiently simple. For example, if both bodies are spherical, and the density of each depends only on the distance from its centre then for the purpose of calculating the overall gravitational forces each body may be replaced by a particle of equivalent mass located at its centre of mass.
Both the Earth and the Moon conform, at least approximately, to the requirements of spherical symmetry described above. It follows that the magnitude of the force that attracts each body towards the other is determined by the product of their masses and the inverse square of the distance between their centres.
On the Earth’s surface we may associate the weight of an object of mass m with the attractive gravitational force exerted by the Earth.
Equating the magnitudes of these forces we find:
$W = mg = \dfrac{GmM_{\rm E}}{R_{\rm E}^2}$
where RE is the radius of the Earth, which is assumed to be spherical, and ME is its mass. Thus
$g = \dfrac{GM_{\rm E}}{R_{\rm E}^2}$(13)
Question T8
Given the universal gravitational constant as above, the magnitude of the acceleration due to gravity as 9.81 m s−2, and the radius of the Earth as 6.38 × 106 m, determine the Earth’s mass.
Answer T8
From Equation 13 $g = \dfrac{GM_{\rm E}}{R_{\rm E}^2}$
therefore$M_{\rm E} = \dfrac{gR_{\rm E}^2}{G} = \rm \dfrac{9.81\,m\,s^{-2}\times(6.38\times 10^6\,m)^2}{6.67\times10^{-11}\,N\,m^2\,kg^{-2}} = 5.99\times10^{24}\,kg$
Question T9
Comment on the following claim. The gravitational attraction between the Earth and the Moon applies forces to each body. Since the Earth is much more massive than the Moon, it applies a much larger force on the Moon than does the Moon on the Earth, and this is why the Moon orbits the Earth, rather than vice versa.
Answer T9
Newton’s law of universal gravitation involves the product of the two interacting masses and the value of this product does not depend on the order of multiplication (i.e. m1m2 = m2m1). Thus the gravitational force on each object has the same magnitude. This is an example of a Newton’s third law pair of forces for two interacting objects. The reason why the force has a more noticeable effect on the Moon is that the Moon has a smaller mass and so the same force causes a larger acceleration on the Moon. In fact the Earth’s motion also shows an orbit – both bodies are actually in orbit about their common centre of mass, but this point is much nearer to the Earth than to the Moon and so the orbital motion is much more noticeable for the Moon.
3.3 Friction between surfaces in contact
We now return to the topic of friction, mentioned in Section 2, to make our discussions of it more quantitative. Friction is important in many ways in everyday life; sometimes it is useful, sometimes very inconvenient. Without friction we could not walk, ride bicycles, drive cars or use nails or screws. On the other hand, when we want to move a refrigerator, we find friction a great nuisance. Friction causes loss of efficiency and increased wear and tear in machinery, producing heat and increased running and maintenance costs. At the macroscopic level, the behaviour of the friction force between two unlubricated solid dry surfaces can be described fairly simply by the following empirical laws, discovered independently by Leonardo da Vinci (1452–1519) and Guillaume Amontons (1663–1705).
- 1
-
The magnitude of the frictional force on a body is proportional to the magnitude of the (normal) reaction that acts on that body.
- 2
-
The frictional force is independent of the (macroscopic) area of contact for a given reaction force.
- 3
-
If two surfaces are caused to slip, the frictional force is independent of the relative speed between the two surfaces, once relative motion has occurred, but less than that just before the relative motion occurs. i
The first of these laws seems reasonable and accords with experience – it is much harder to pull a sledge at a given velocity when someone sits on it than when it is empty.
✦ Would you say that the second friction law is expected?
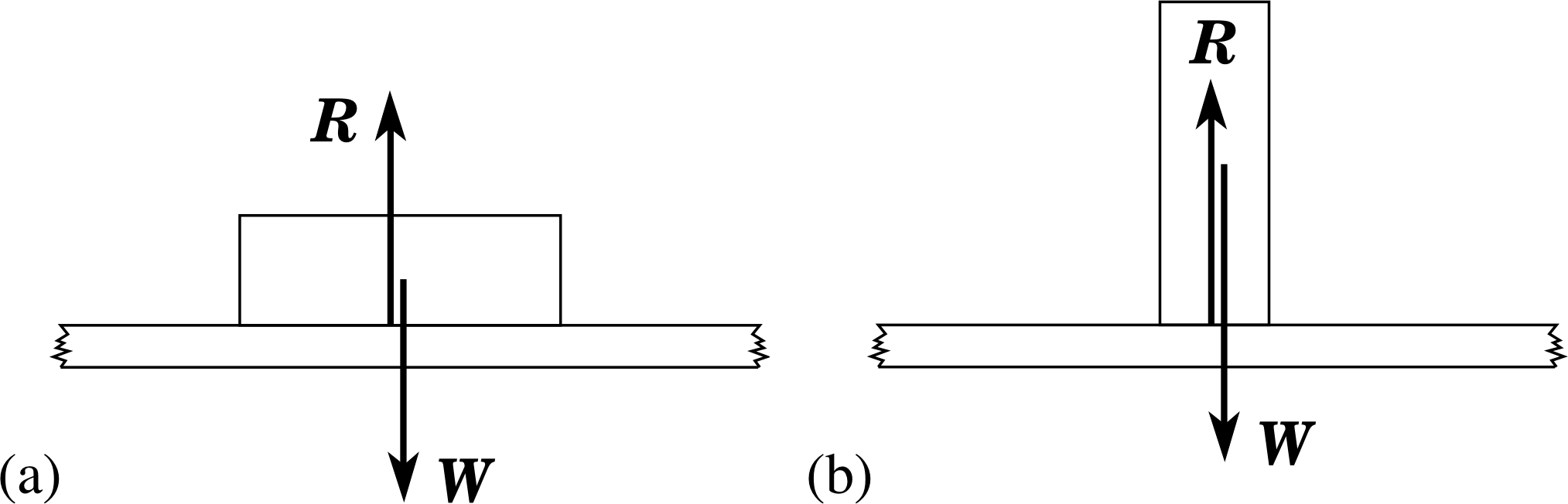
Figure 5 (a) A rectangular block of weight W lies with its larger face in contact with a horizontal plane. (b) The same block lies with its smaller face in contact with the horizontal plane. The reaction R is the same in both cases.
✧ It seems rather unexpected. We might anticipate that if the same weight is spread over a larger surface area, as in Figure 5, then there would be a greater contact area and therefore more friction.
The explanation is that the frictional force is determined by the microscopic, not the macroscopic, contact area. At a microscopic level, all surfaces show marked irregularities. When two surfaces are in ‘contact’ they meet only at the peaks of these irregularities and the real contact area is very much less than the apparent macroscopic contact area. As we spread the weight there are more, but less deformed, contact regions and the result of this is that the real contact area remains virtually the same so that the frictional forces appear to be more or less unchanged.
✦ The third of the empirical laws claims that the frictional force does not depend on the relative speed of the two faces. Would you expect this to remain true as the relative speed becomes very small?
✧ We know that as the relative speed shrinks to zero the frictional force becomes larger, it cannot then be independent of relative speed at very low speeds.
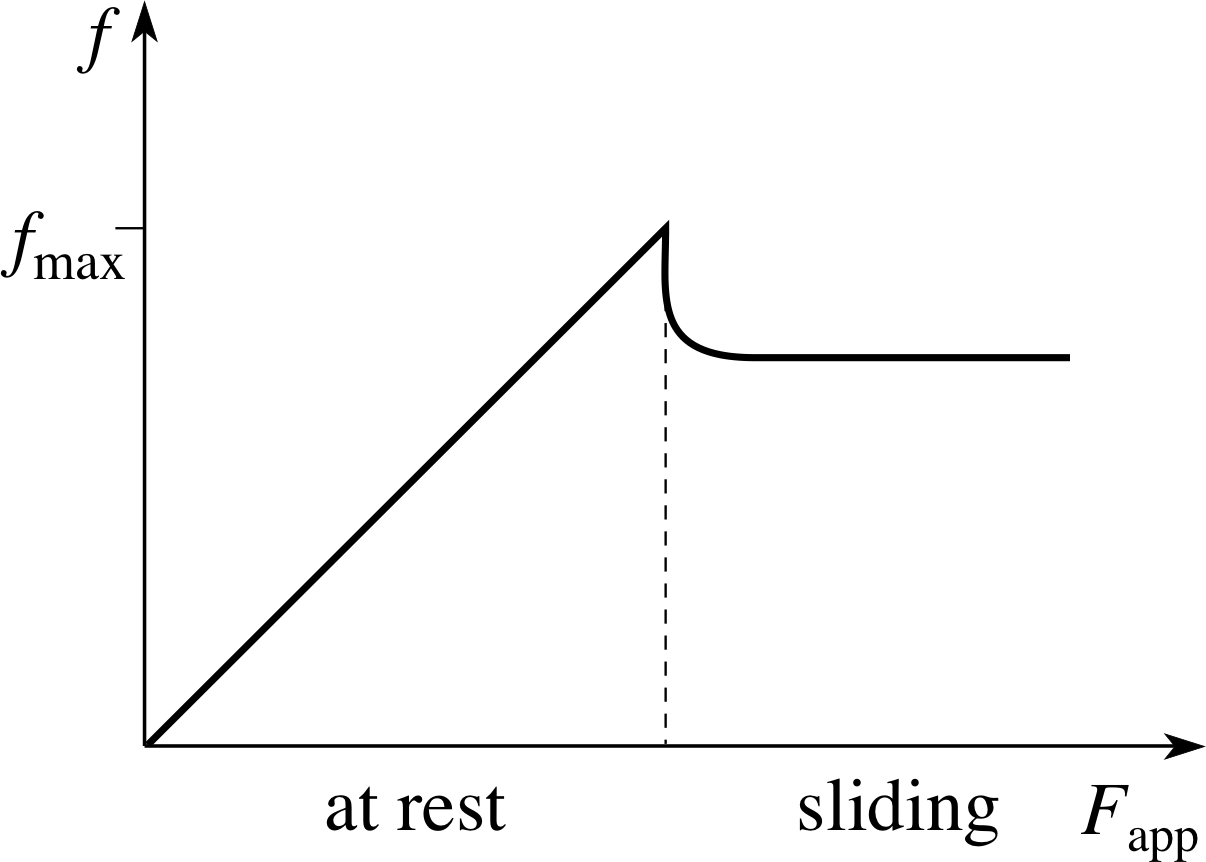
Figure 6 Variation of the magnitudes of the frictional force f and applied force Fapp.
Experiments show that the frictional force is also slightly smaller for very high speeds. From everyday experience we know it takes a certain minimum applied force to start a body sliding over a horizontal surface. However, once sliding starts, a smaller applied force is enough to keep the body moving at constant velocity – any driver who has braked on ice or taken a bend too quickly, knows this very well! Up to now we have only talked about ‘friction’. However, we should distinguish between static friction, which occurs before sliding occurs, and sliding friction, which occurs during sliding.
If we apply a horizontal force Fapp to a stationary body lying on a horizontal surface, and the body does not move, then the frictional force (f = −Fapp) on the body must have the same magnitude as Fapp. As Fapp is increased, the magnitude of f increases to match it exactly until a critical value fmax is reached. When Fapp is increased further, the block starts to slide and f rapidly falls to a lower value which then remains reasonably constant.
The relation between f and Fapp is illustrated in Figure 6.
The first empirical law of friction, that tells us that the magnitude of the friction force is proportional to the magnitude of the reaction force, allows us to define two coefficients of friction, one for static friction, and one for sliding friction:
fstatic = μstatic R(14)
fslide = μslide R(15)
Equations 14 and 15 define the coefficient of static friction, μstatic and the coefficient of sliding friction, μslide. Since both these coefficients relate the magnitudes of two forces, they are dimensionless quantities. Since it takes a larger force to start a body moving than to keep it moving, it is clear that, in general, μstatic > μslide. For example, for tyre rubber on tarmac μstatic ≈ 1, whereas μslide ≈ 0.7.
✦ Can Equations 14 and 15 be made into vector equations by simply replacing the magnitudes of the respective forces by their appropriate vectors, with a negative sign if necessary?
✧ We cannot do this, with or without a negative sign, since the vector R is normal to the surface but the frictional force vectors are parallel to the surface, in a direction opposite to that of the motion.
Question T10
Determine the acceleration of a block of mass 2.0 kg which is pushed along a level surface by a horizontal force of magnitude 9.5 N, given that μslide = 0.25.
Answer T10
Let the magnitudes of the forces acting be FP for the pushing force, f for the frictional force and R for the normal reaction force. Applying Newton’s second law to the mass m, with the acceleration along the x–axis, we find the resultant force Fx is:
Fx = FP − f = max
withf = μR = μmg
somax = FP −μmg
andax = (FP/m) − μg = (9.5 N/2.0 kg) − (0.25 × 9.8 m s−1) = 2.3 m s−2
Question T11
A block is placed on a plane and the angle of inclination of the plane to the horizontal is gradually increased until, at the angle θ, the block starts to slide. Show that μstatic = tan θ.
Answer T11
Since the acceleration is directed down the plane we take this to be the x–axis, with the y–axis perpendicular to and out of the plane. When the block starts to slide, the component of its weight along the plane is just equal and opposite to the maximum friction force, of magnitude fmax, directed up the plane so:
along the plane: mg sin θ − fmax = 0
perpendicular to the plane: R − mg cos θ = 0
Substituting for R we find
fmax = μstatic R = μstatic mg cos θ
somg sin θ = μstatic mg cos θ
andμstatic = sin θ/cos θ = tan θ
Air resistance is another familiar form of friction. It is known to any cyclist or motorist and is of such technological importance in today’s world that it has been studied in great detail. It is found experimentally that it varies with the profile presented to the air flow and with the size and relative speed of the moving object. For spheres of radius r moving at speed υ through still air it is found that the magnitude of the frictional force is proportional to:
rυ at low speeds when rυ < 10−4 m2 s−1 (where there is streamlined flow of the air);
r2υ2 at higher speeds (where there is turbulent flow of the air).
At very high speeds (rυ > 1 m2 s−1) the dependence is even more complicated. Most everyday objects, even though not spherical, display theυ2 dependence and this is one reason why there is a rapid increase in car fuel consumption at high speeds.
3.4 Tension and compression forces
When a string (or cable, chain, etc.) attached to a body is pulled taut the string is said to be under tension. The tension is the force exerted by one section of the string on the next section, or on the body attached to the end.

Figure 7 Tension forces T1 and T2 act on a short section of mass m of a string.
Consider a short section of string of mass m acted on by tension forces T1 and T2, of magnitudes T1 and T2, as shown in Figure 7. If we apply Newton’s second law to this section we obtain:
max = T1 − T2
From this it can be seen that if the string is not accelerating, so that ax = 0, (or if m = 0) then T1 = −T2 and T1 = T2. Thus, if the velocity of the string is constant, or if the mass of the string is negligible compared with the masses of bodies attached to the string, then the magnitude of tension is the same throughout the string. In dealing with problems in mechanics, it is common practice to treat a string connecting bodies as an ideal string, by which we mean that the string has negligible mass and does not stretch, i.e. it is a light inextensible string.
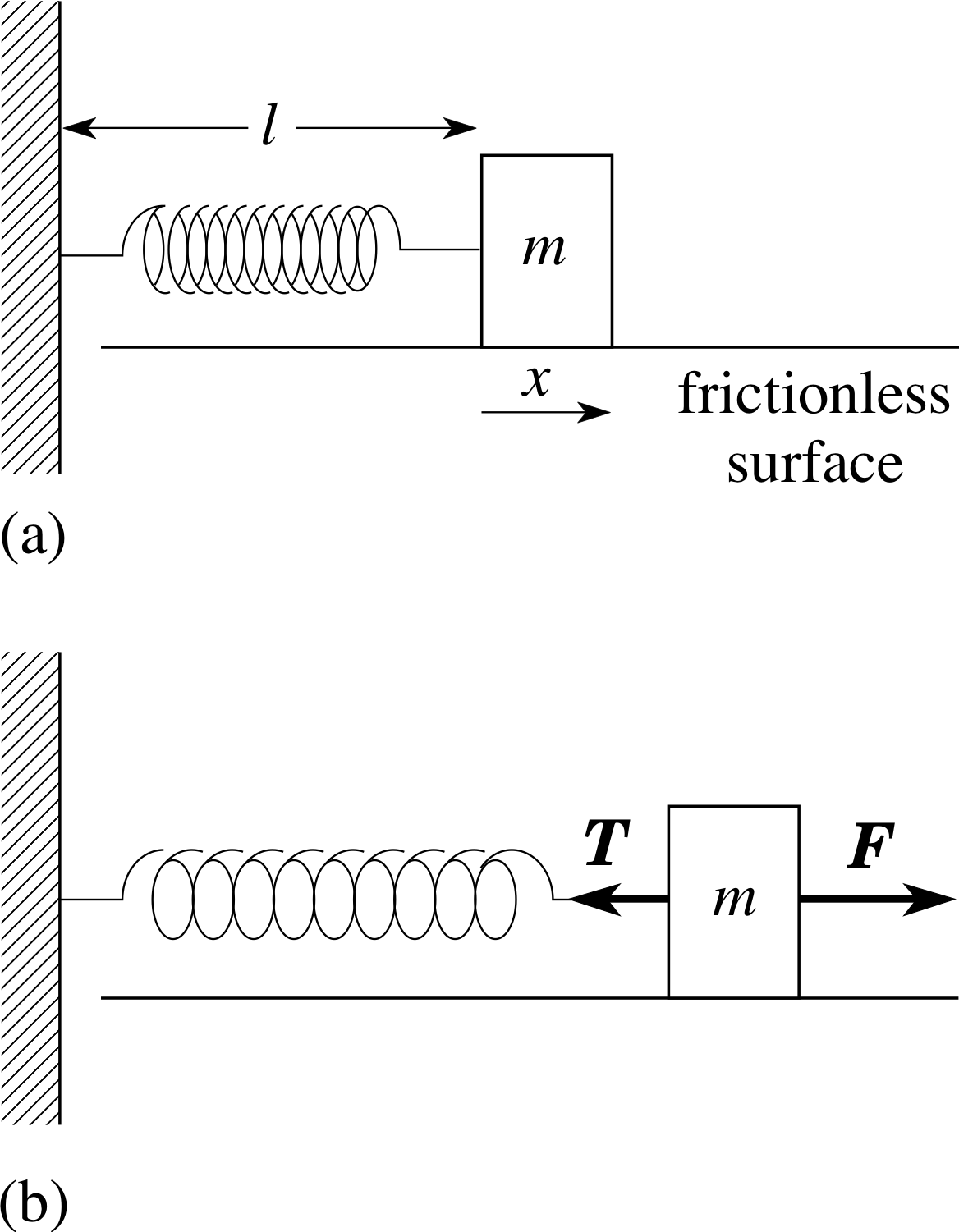
Figure 8 Force stretching an elastic spring against the spring tension. Note that the direction of T ensures that Tx will be negative. When the system in (b) is in equilibrium, the forces T and F will be equal in magnitude but acting in opposite directions.
Sometimes we have to deal with more realistic strings or springs which do stretch. The difference between a string and a spring is that a string can only sustain tension and can only pull an attached object, whereas a spring can also be under compression and can push an object. We met an example of compression in Subsection 2.3, in explaining the mechanism of the reaction force. An idealized extendable string or spring is called an ideal elastic string or ideal spring. Ideal elastic strings and springs have the property that as their lengths are changed beyond their unstretched length the tension changes linearly with the extension (for a spring the ‘extension’ may also be negative as the tension becomes a compression).
Thus, ideal springs obey Hooke’s law which states that the magnitude of the applied force Fx required to produce an extension x is given by:
Hooke’s law Fx = ksx(16)
The constant ks is called the spring constant, and is a measure of the stiffness of the spring. Equation 16 gives the units of ks as N m−1. Fx is in the direction of the extension and so the tension force Tx is in the opposite direction to the extension, and acts to restore the spring to its original length. In most cases we are concerned with the tension force which a spring exerts on an object attached to its end. This force is in the opposite direction to the extension x and its value is given by the equation:
Tx = −ksx i
An elastic string behaves like a spring, except that it cannot be compressed. See Figure 8.
Many real strings and springs behave elastically and obey Equation 16 provided they are not stretched beyond their elastic limit; beyond this extension the linearity is lost and permanent deformation could occur (i.e. if the force was released the spring would not return to its unstretched length).
Question T12
A spring rests on a horizontal frictionless surface with one end fixed and the other attached to a particle of mass 0.5 kg. If the particle is displaced along the line of the spring such that the spring is stretched by 0.25 m, and then the particle is released, the magnitude of the initial acceleration is found to be 2.0 m s−2. Find the spring constant.
Answer T12
A spring of spring constant ks, stretched through a distance x, applies a tension force Tx = −ksx to an attached particle of mass m, causing the particle to accelerate with an initial acceleration ax(here ax = −2.0 m s−1).
Newton’s second law gives:
max = Ts = −ksx and so ax = −ksx/m
soks = −max /x = −0.5 kg × −2.0 m s−1/0.25 m = 4 N m−2
Hooke’s law, the law of terrestrial gravitation, the law of universal gravitation and the laws of friction are examples of force laws. These are the rules that allow us to predict the forces acting in any given physical situation.
3.5 Summary of Section 3
The gravitational force exerted by the Earth on a body is called the weight W of the body, and its magnitude is related to the mass m of the body by the equation W = mg, where g is the magnitude of the acceleration due to gravity. Terrestrial gravity is a special case of universal gravity, as described by Newton’s law of universal gravitation. i
When an increasing force is applied to a stationary body lying on a surface, the frictional force exerted on the body by the surface gradually increases to exactly oppose the applied force. Eventually, the frictional force reaches a maximum, and then, as the body starts to slide, drops to a lower value. When a body slides over a surface the frictional force on the body is proportional to the magnitude of the normal reaction which the surface exerts on the body, and is independent of the area of contact and the relative speed.
For a non–accelerating light inextensible string, the tension force is the same throughout the string. For ideal elastic strings or springs, the tension is directly proportional to the extension produced. The same is true of many real elastic bodies provided they are not stretched beyond their elastic limit.
4 Forces in equilibrium; statics
4.1 Objects at rest
An object at rest that has no unbalanced force acting on it is said to be in static equilibrium. The study of such systems is called statics. We met an example of statics in Subsection 2.3 where we described an object at rest on a surface, under the combined effect of two balanced forces. These two forces were the weight, W, acting downwards and the reaction force R from the surface, acting upwards. Since there is no acceleration, W = −R and the total force F = W + R = 0. More generally, if a body is subject to N different forces F1, F2, ... FN then a necessary condition that must be satisfied if that body is to be in static equilibrium is that the vector sum of the forces should be zero, i.e.
$\displaystyle \sum_{i=1}^N \boldsymbol F_i = \boldsymbol 0$(Eqn 4)
✦ Is this necessary condition for static equilibrium also a sufficient condition? In other words, if the condition is satisfied does it guarantee that the body will be in static equilibrium?
✧ No. The condition ensures that the body does not accelerate, but it does not prevent it from moving with constant velocity.
Question T13
Draw vector diagrams to illustrate the situation in which a particle is in static equilibrium under the combined action of several forces acting in a plane, for the cases where: (a) there are three forces, each of the same magnitude; (b) there are four forces, each of the same magnitude; (c) there are four forces, all of different magnitudes. What is the common feature of all these diagrams? [Hint: Draw the vectors ‘head-to-tail’.]
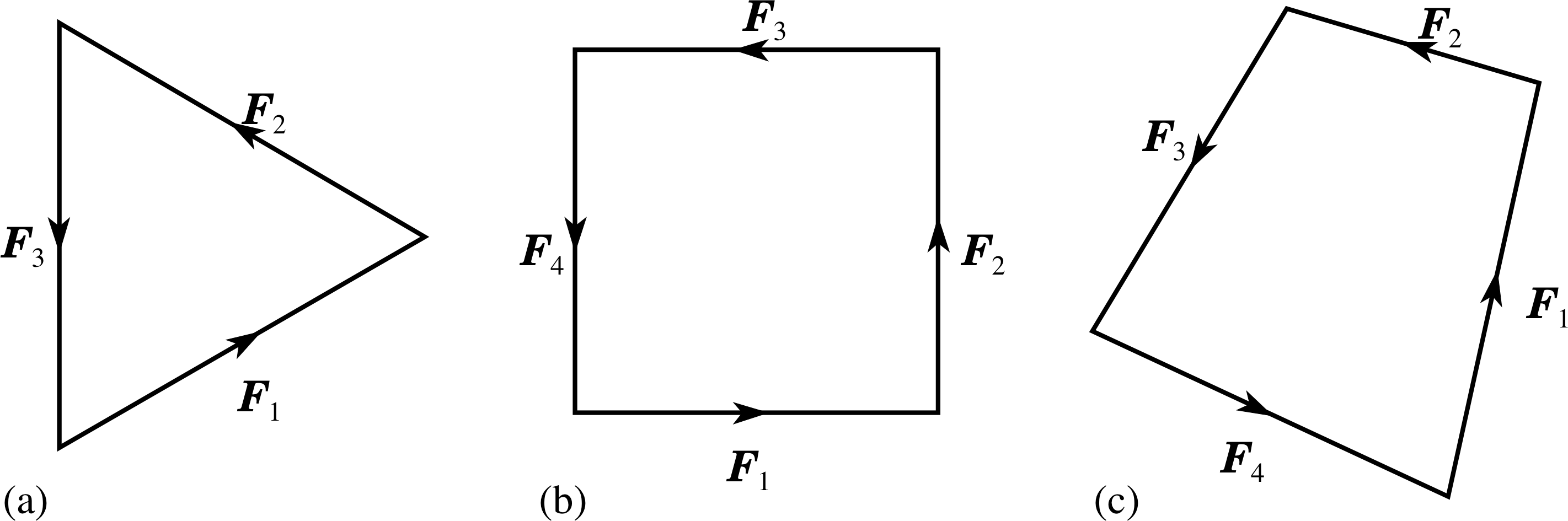
Figure 15 See Answer T13.
Answer T13
The three vector diagrams are shown in Figure 15. In drawing these diagrams, the initial point of the next vector should coincide with the terminal point of the previous vector, i.e. the vectors must be placed nose-to-tail.
If the diagram is constructed correctly then the resultant is zero and the initial point of the first vector coincides with the terminal point of the last vector, so that the diagram is a closed polygon, with all the arrows pointing the same way round the polygon.
4.2 Objects in uniform linear motion
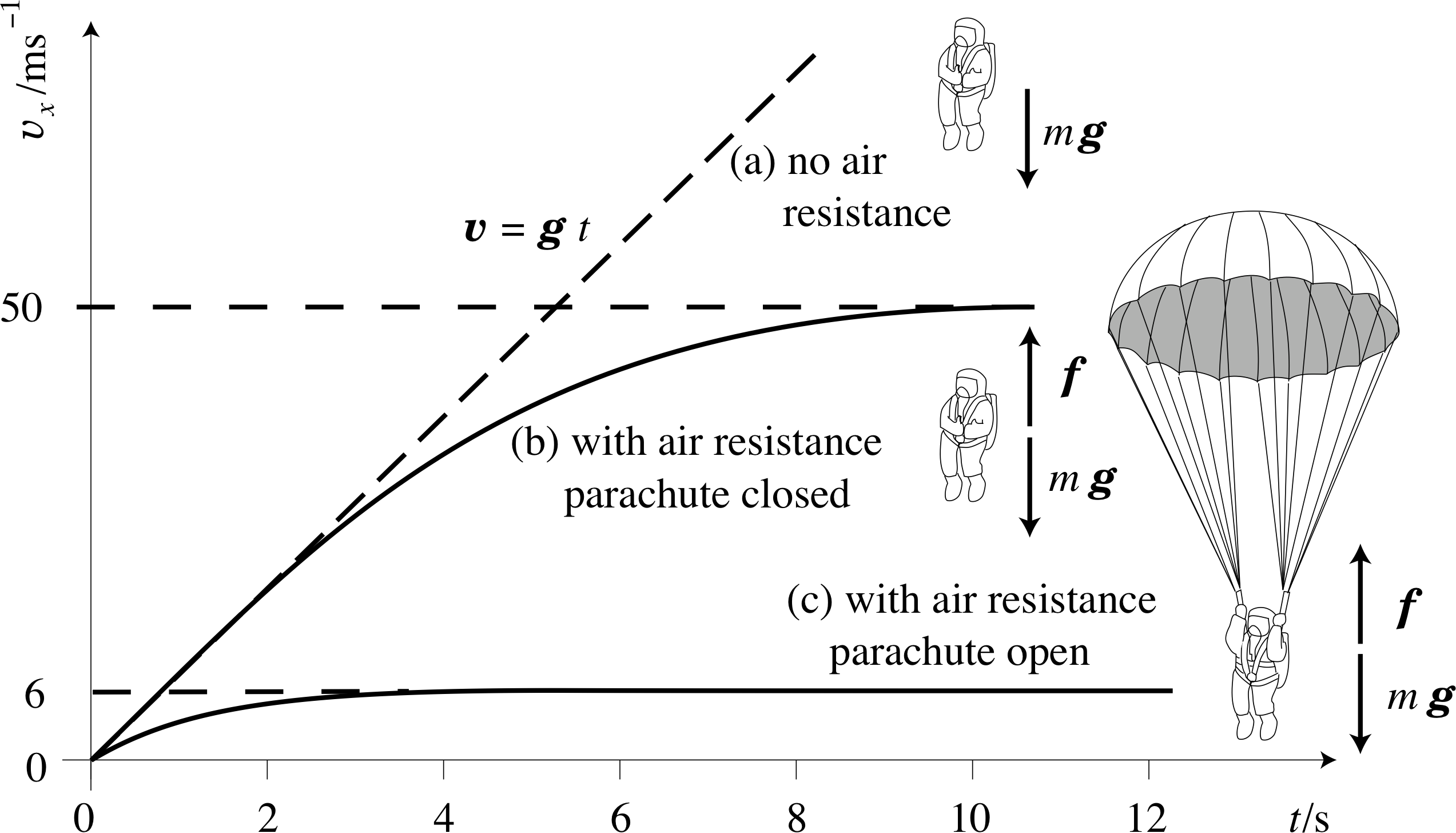
Figure 9 (a) In the absence of air resistance, a free–falling parachutist has a constant acceleration g of magnitude 9.8 m s−2. (b) Air resistance reduces the acceleration as the velocity increases, and at the terminal velocity the acceleration is zero. (c) The parachute provides greater air resistance for a given downward velocity, so the terminal velocity is smaller than in (b).
Newton’s first law draws no distinction between a body in uniform motion and one at rest – it is simply a difference of our own inertial frame of reference. For example, consider a parachutist jumping from a stationary balloon. If there were no air resistance gravity would produce an acceleration downwards of magnitude g, as in Figure 9a. However, air resistance provides an upward force f acting against the weight W (Figure 9b).
This air resistance opposes motion and its magnitude rises with the speed of the motion, gradually reducing the downward acceleration. Eventually, at a particular velocity, υT, the terminal velocity, f balances the weight W, the resultant force then becomes zero and the parachutist continues to fall at this terminal velocity. Unfortunately, the terminal speed υT with a closed parachute is too high for there to be a comfortable outcome when the ground is reached! With the parachute open, the terminal speed is much lower, as in Figure 9c, but the point remains that as long as the resultant force is zero there is no acceleration. We can combine our conclusions for motion of a body where there is no resultant force acting, by defining the term translational equilibrium.
A body is said to be in translational equilibrium if it has constant velocity (including the possibility of υ = 0). A body is in translational equilibrium if and only if the resultant force acting on it is zero i
$\displaystyle {\boldsymbol F} = \sum^N_{i=1} {\boldsymbol F}_i = 0 $
This implies that each of the components of F must be zero (i.e. Fx = Fy = Fz = 0). It follows that in any other direction, chosen at random, the component of the resultant force must be zero.
Question T14
Three horizontal forces act on a body lying on a frictionless, horizontal surface and keep it in translational equilibrium. One force acts due north, the second due east and the third, of magnitude 10 N, acts in a direction 60° west of south. Find the magnitudes of the forces in the east and north directions.
Answer T14
Let FN and FE be the magnitudes of the forces in the north and east directions, respectively. If we consider the components along the north–south direction, we find
FN = 10 cos 60° = 5 N
Considering components along the east–west direction:
FE = 10 cos 30° = 8.66 N
5 Non–equilibrium situations; dynamics
Dynamics is the branch of mechanics in which we analyse the non–uniform motion of bodies. If a body is moving non-uniformly, i.e. it is accelerating, then clearly the resultant of the forces acting on it is not zero. The problems of dynamics are almost all concerned with the relation between the forces acting on bodies and the resulting motions. In this section we will look at some of the simpler types of problems which arise, and lay down some ground–rules for their systematic solution.
5.1 Using components of force and acceleration
Consider the following problem:
A block of mass 50 kg is pulled along a horizontal surface by means of a light, inextensible string which is inclined at an angle of 20° to the horizontal. The magnitude of the tension in the string is 95 N and the frictional force at the surface is of magnitude 10 N. Find the acceleration of the block and the reaction force exerted on the block by the surface.
There are two main ways of tackling problems of this type: we can either find the total resultant of the forces acting by drawing a scale diagram, or alternatively examine algebraically the components of the forces acting. The second method is usually more easily applied – in fact it can always be applied – while the first, although it will sometimes give a quick and easy solution to a problem, will often lead to complications and extra opportunities for making mistakes.
The following guidelines for setting about a problem should reduce the chance of errors. As you become more expert in handling these problems you will find what short cuts you can take but it is best to be cautious at first.
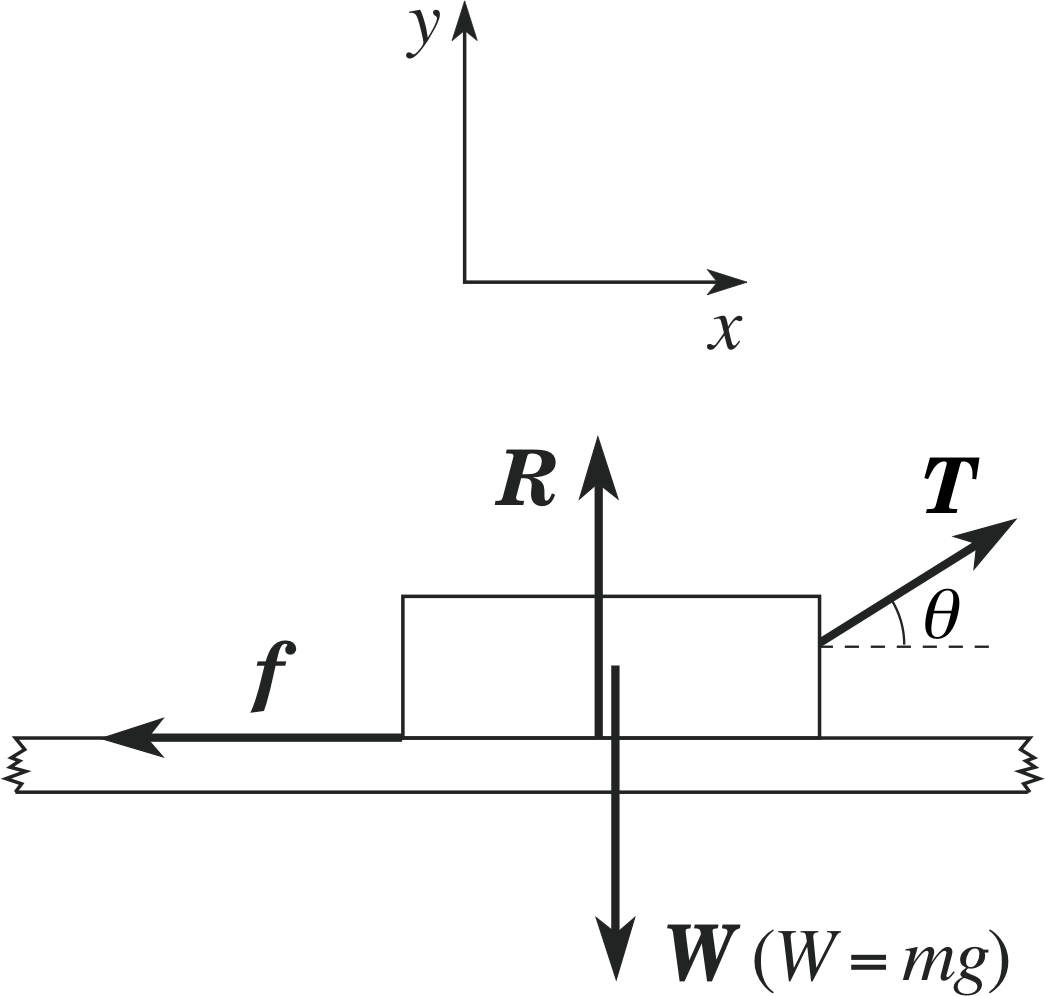
Figure 10 A tension force T is applied at an angle θ to the horizontal to a block of weight W (W = mg). The friction force f opposes the motion. R is the reaction force exerted on the block by the surface. The two forces act through the centre of mass. The vector arrows have been separated in the figure for clarity.
- 1
-
Draw a clear diagram of the system to be analysed, showing the axes of your inertial frame of reference (in which Newton’s laws are valid).
- 2
-
Indicate on the diagram all the forces acting on each body of interest. Avoid confusing the picture; do not include forces on other bodies and, in particular, third law pair forces not acting on the bodies of interest.
- 3
-
Choose the directions in which to take components. Usually, the direction of the acceleration, if known, is chosen as one component direction. This choice implies that the components of the acceleration in directions perpendicular to the chosen direction will be zero.
- 4
-
Apply Newton’s second law in component form, and use appropriate force laws where necessary, to provide the equations needed to find the unknowns.
- 5
-
Solve the equations, check that the solutions are sensible and that all quantities have appropriate units and signs.
We will now apply this procedure to our problem.
We have to find the acceleration along the surface and the reaction force. Applying the above guidelines to our problem, we first draw the diagram, with the coordinate axes shown, and indicate all the forces acting on the block, (see Figure 10).
The four forces acting on the block are the weight W (W = mg), the reaction force R, the friction f and the tension force (the ‘pull’ of the string) T.
Providing the block does not lift off the surface, the acceleration vector must be along the surface, with no component perpendicular to the surface. We will therefore choose the axes of our inertial frame of reference so that the x–axis is along the surface and the y–axis perpendicular to the surface.
✦ It would be wrong here to jump to the conclusion that R = mg, arguing that action and reaction are equal and opposite. Why?
✧ In the first place, as explained in Subsection 2.3, the reaction R is not the third law pair of the mass because both forces act on the same object. Moreover, the tension force also has a component along the y–direction and it is the total force component along y which is zero. The force T reduces the reaction force from the surface by partially supporting the block.
Following step 4, we apply Newton’s second law along the x– and y–directions:
horizontally, along the x–direction:max = Tx + fx = T cos θ − f i
vertically, along the y–direction:0 = Ry + Ty + Wy = R + T sin θ − mg
If we rearrange these equations it follows that:
ax = (T cos θ − f)/m and R = mg − T sin θ
If we substitute in known values for the quantities T, θ, f and m, we obtain:
$a_x = \rm \dfrac{(95\cos 20°-10) \,N}{50\,kg} = 1.6\,m\,s^{-1}$
andR = (50 kg × 9.8 m s−2) − (95 sin 20°) N = 4.6 × 102 N
Question T15
In the above problem we assumed that the block did not lift off the surface as it was pulled. However, as we have just seen, the tension force reduces the reaction force. For the data in the above problem determine the tension force necessary to just lift the block off the surface and also the acceleration along the surface at this critical condition.
Answer T15
If the block is just about to lift off the surface then the reaction force from the surface, R, has just shrunk to zero but Fy is still zero. Since f = μslide R and R = 0 it follows that f = 0. The acceleration ax is due exclusively to the x–component of T. At the critical condition we have:
along the x–direction: max = T cos θ
along the y–direction: mg = T sin θ
This gives T = mg/sin θ and, eliminating T, we find
ax = g cot θ
Ifθ = 20° then
$T = \rm \dfrac{4.9\times10^2\,N}{\sin 20°} = 1.4\times10^3\,N$
and$a_x = \rm \dfrac{9.8\,m\,s^{-2}}{\tan 20°} = 27\,m\,s^{-2}$
5.2 Motion of coupled bodies
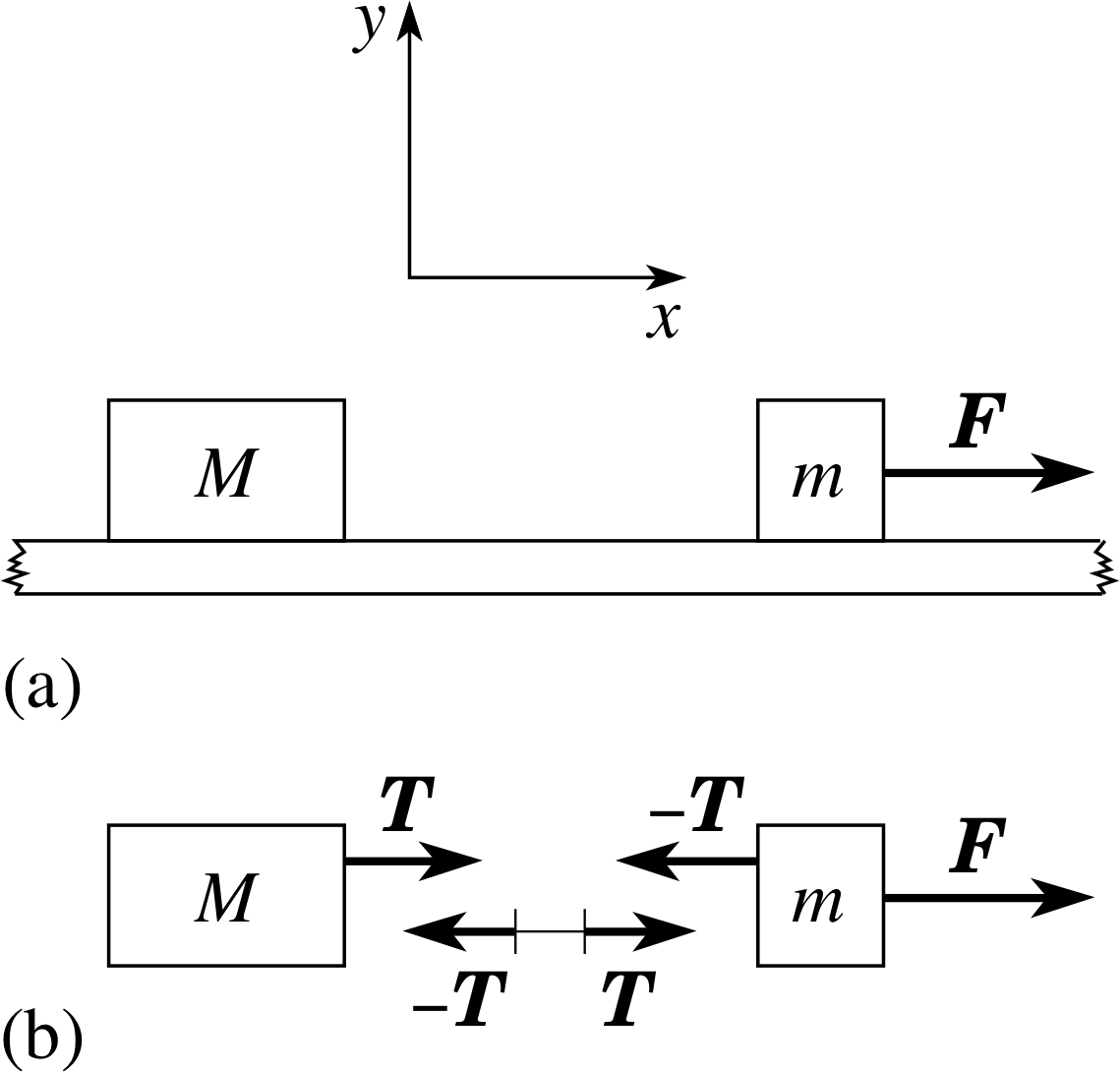
Figure 11 (a) Blocks of mass m and M connected by a string are pulled along by means of an applied force F. (b) The horizontal forces acting on the various parts of the system.
In some problems in dynamics bodies are coupled, for example, by means of connecting strings. It is worth considering such problems separately, as there are particular features of them which need to be appreciated. As an example, consider the problem of finding the acceleration of the two blocks shown in Figure 11a which are connected by a light, inextensible string, and are pulled along a horizontal frictionless surface by an applied force F.
Here again we use the surface to define our coordinate system. We may ignore the weights of the two blocks and the normal reactions of the surface since they cancel along the y–direction and do not enter the problem. We only need consider the accelerations along the horizontal x–direction. The block of mass M is subject to a tension force T which has a positive component +T in the x–direction. The block of mass m is subject to two horizontal forces, a tension force −T and the externally applied force F, consequently the resultant component in the positive x–direction is F − T. i
Now, if the string remains taut while the blocks accelerate it must be the case that the x–component of acceleration of each block must be the same. Calling this common component ax we may apply Newton’s second law to each of the blocks to obtain
Max = T and max = F − T
Eliminating T, it follows that max = F − Max
soax(M + m) = F
i.e.$a_x = \dfrac{F}{M+m}$
This is just the answer we would have found had we treated the two blocks as one, with a mass (M + m), subject to the same force – as if they had been connected by a rigid rod. The substitution of the string with a rigid rod is legitimate here but it is dangerous to assume that one can do this without careful thought. If, for example, we suddenly reversed the force F, then the block m would slow down, stop, and reverse direction, while M would continue with a constant velocity until it collided with m. This is a case where it would not be valid to take a short cut, because the connecting string does not stay taut.
Often, in coupled–body problems which involve strings, pulleys are introduced as a means of changing the line of action of the tension in the string. Providing that a pulley can be considered to be frictionless and of negligible mass, it plays no part in determining the values of the forces and accelerations.
Question T16
Blocks A, B and C with masses 1, 2 and 3 kg, respectively, lie in a line in contact on a frictionless, horizontal surface. The blocks are pushed along by means of a horizontal force of magnitude 12 N applied to block A towards B and C. Find the acceleration of the blocks and the force exerted on block B by block A.
Answer T16
If mA, mB and mC are the masses of the blocks and F is the magnitude of the applied force, then, applying Newton’s second law to the whole moving system we find
(mA + mB + mC) a = F
thereforea = F/(mA + mB + mC) = 12 N/6 kg = 2 m s−1
To find FBA, the force exerted on block B by block A, apply Newton’s second law to blocks B and C as a system:
(mB + mC) a = FA = 5a = 10 N
5.3 Centripetal force
If a body moves in a circular path then it has an acceleration, even though its speed may be constant. This is because the direction of motion, and hence the velocity, is continuously changing. If the speed υ is constant, the motion is said to be uniform circular motion. It may be shown that in this case the acceleration has magnitude υ2/r, where r is the radius of the circle, and it is directed radially inward, towards the centre of the circle. This acceleration is called the centripetal acceleration. i
From Newton’s second law it follows that there must be a force directed towards the centre of the circle, associated with this centripetal acceleration. This force is called the centripetal force, and it has magnitude mυ2/r, where m is the mass of the body. The term ‘centripetal’ simply indicates the direction of the force; towards the centre of the circle. It does not tell us anything about the nature of the force. A centripetal force may be provided, for example, by a tension in a string, a gravitational force, an electric force or a magnetic force.
If the speed of the circular motion is not constant, then there is also a tangential component of acceleration in addition to the centripetal component. It follows that, in such cases, there must be a force component tangential to the circle in addition to the centripetal component of force.
A term frequently used in everyday life is centrifugal force. This ‘force’ is supposed to be responsible for tending to make objects fly outwards as they move round a bend or rotate on a turntable. It is a complete invention, with no physical basis in fact and it is a term best avoided. We mention the term here mainly because it is a term in common use. The invention of centrifugal force stems from the incorrect belief that Newton’s laws hold in any frame of reference, rather than only in an inertial frame of reference. As we discussed in Subsection 2.1, Newton’s laws are not valid in an accelerated frame of reference and a turning or rotating frame of reference is just such a frame. Fictitious forces appear to act if we insist on applying the laws where they are invalid. As viewed in the rotating frame, an object released from rest will accelerate, so an unbalanced force must be invented to explain this if Newton’s laws are (incorrectly) assumed to be valid in such a frame. An observer in an inertial frame outside, watching this event, will explain it (correctly) in terms of the absence of the ‘real’ centripetal force which is necessary to keep an object moving along the circular path. i
Any coordinate system which is rotating is a non–inertial frame. Strictly speaking, the Earth itself does not provide a truly inertial frame because of its rotation about its axis and its orbit around the Sun. Usually the consequences of ignoring these rotations are small and hence we frequently use the Earth as an inertial frame when considering problems in mechanics – but there are some interesting exceptions.
For example, the weight of a body is slightly less at the Equator than it is at the poles, as gravity must provide the additional centripetal force needed at the Equator; on a global scale, the air circulation around high and low pressure regions is opposite in the Earth’s two hemispheres; erosion of riverbanks by large rivers is influenced by the Earth’s rotation.
5.4 The conical pendulum
The following example illustrates several of the features discussed in this section.
Example 1
One end of a light inextensible string is secured to a fixed point P and a particle of mass m is attached to the other end. The particle is projected so that it travels in a horizontal circle of radius r with constant speed υ, the string making an angle θ with the vertical throughout the motion. This oscillatory system is called a conical pendulum. i Let us find υ in terms of r and θ.
Solution

Figure 12 Force diagram for the conical pendulum.
There are only two forces acting on the body; the weight W acts vertically downwards (W = mg ) and the tension force T from the string acts along the line of the string. The force diagram is shown in Figure 12.
The acceleration of the body is directed towards the centre of the circle at O and is of magnitude υ2/r. Following the advice given in Subsection 5.1, we apply Newton’s second law along the direction of the acceleration. The only force component acting on the body in this direction is the x–component of T, −T sin θ, and so this must be the centripetal force at the instant shown. There are no components of acceleration or resultant force along the y–direction.
From Newton’s second law:
along the x–direction max = −mυ2/r = −T sin θ
along the y–direction 0 = T cos θ − mg
these two equations can be rearranged and then equated to give:
$T = \dfrac{mg}{\cos\theta} = -\dfrac{ma_x}{\sin\theta} = \dfrac{m\upsilon^2}{r\sin\theta}$
somυ2/r = T sin θ = mg tan θ
and finally υ2 = gr tan θ
✦ Show that the dimensions balance in this equation.
✧ The dimensions of υ are length divided by time [L]/[T]. The dimensions of g are length divided by time squared [L]/[T2].
The term tan θ is dimensionless, and r has dimensions of length [L]. Hence the dimensions of gr tan θ are [L2]/[T2], as expected.
6 Closing items
6.1 Module summary
- 1
-
The fundamental laws governing the behaviour of forces are Newton’s three laws of motion.
- 2
-
Newton’s first law of motion introduces the concepts of force as that which is responsible for changing motion, and inertia as the property of a body tending to maintain its state of motion. Frames of reference in which Newton’s first law is valid are called inertial frames.
- 3
-
Newton’s second law of motion quantifies the concepts of force and mass by relating the resultant force F on a body of mass m to the acceleration a produced, through the equation F = ma.
- 4
-
Newton’s third law of motion states that forces between interacting bodies always occur in pairs, in which the forces on each body have equal magnitudes but opposite directions.
- 5
-
The weight of a body of mass m near the Earth is the force acting on it due to the Earth’s gravity, it is directed vertically downwards and has magnitude equal to mg, where g is the magnitude of the acceleration due to gravity.
- 6
-
The force of contact friction reaches a maximum value just before sliding occurs and then drops to a lower value. Its magnitude is proportional to the magnitude of the reaction force keeping the surfaces in contact.
- 7
-
The tension in a light inextensible string has constant magnitude throughout the string.
- 8
-
The extension of ideal elastic strings and springs is described by Hooke’s law, which states that the extension is proportional to the applied force, up to the elastic limit. For springs the law also applies to compression.
- 9
-
Translational equilibrium is the state in which a body has constant velocity, which may be zero. The condition for this state is that the vector resultant of all the forces acting on the body is zero.
- 10
-
Unbalanced forces acting on a body cause it to accelerate. Newton’s second law in component notation allows the solution of problems of motion for coupled bodies, bodies on inclined planes or in circular motion (involving centripetal acceleration and centripetal force).
6.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
State Newton’s first law of motion, explain how it introduces the concept of force and how it may be used to define an inertial frame of reference.
- A3
-
State Newton’s second law of motion for a body of constant mass and explain how it enables force to be quantified.
- A4
-
State Newton’s third law of motion and identify third law force pairs for any pair of interacting bodies.
- A5
-
Express Newton’s three laws of motion in vector form.
- A6
-
Distinguish between weight and mass, and describe the relation between them. Distinguish between terrestrial and universal gravitation and explain the relationship between them on the basis of Newton’s law of gravitation.
- A7
-
Describe the operation and variation of friction between surfaces in contact, and distinguish between static and sliding friction.
- A8
-
State and use Hooke’s law for an elastic string or spring.
- A9
-
Solve a variety of simple problems involving bodies in translational equilibrium.
- A10
-
Solve a variety of simple problems involving bodies not in translational equilibrium.
- A11
-
Use Newton’s laws of motion to solve problems involving coupled bodies, centripetal forces and motion down inclined planes.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
6.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
Explain what is meant by the term ‘inertial frame of reference’ and discuss whether a frame of reference fixed on the Earth is such a frame.
Answer E1
An inertial frame of reference is one in which Newton’s first law of motion is obeyed. Since the Earth rotates about its axis and is in orbit around the Sun, it has acceleration components. Strictly, then, it cannot be a true inertial frame of reference, but over a small area it acts as a good approximation to an inertial frame.
(Reread Subsection 2.1 if you had difficulty with this question.)
Question E2 (A3 and A10)
A given force applied to three bodies in turn produces accelerations with magnitudes in the ratio of 2 : 3 : 1. What is the ratio of the masses of the bodies?
Answer E2
Let m1, m2 and m3 be the masses, and a1, a2 and a3 the magnitudes of the accelerations produced. Using Newton’s second law, applied in the direction of the force:
F = m1a1 = m2a2 = m3a3
Therefore, given that a1 : a2 : a3 = 2 : 3 : 1
we have2m1 = 3m2 = m3
andm1 : m2 : m3 = 3 : 2 : 6
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E3 (A4)
An object is stationary on a table. What force is associated with the weight of the object by Newton’s third law?
Answer E3
The weight of the object is the downward gravitational force that the Earth exerts on the object. Hence the associated Newton’s third law force is the upward gravitational force that the object exerts on the Earth. Note that it is not the ‘reaction’ force from the table, which is the third law pair force with the force that the object exerts on the table. For example, the table may not be able to sustain the weight of the object and then the reaction force from the table on the object would be less than the weight of the object – at the moment of contact the table would break and the object and the table would then accelerate downwards!
(Reread Subsection 2.3 if you had difficulty with this question.)
Question E4 (A3 and A6)
Derive the relationship between the mass and the weight of a body, and explain what happens to the value of each of these quantities when the body is taken from the Earth to the Moon.
Answer E4
If a body of mass m is allowed to fall freely its acceleration has a magnitude g. The downward gravitational force exerted on the body by the Earth is the weight W. The magnitude of the weight is related to the mass (through Newton’s second law) by:
W = mg
When the body is taken to the Moon its mass, which is an intrinsic property of the body, does not change. However, since the value of g on the moon is about one–sixth of its value on Earth, then the weight is also about one–sixth of the value on Earth.
(Reread Subsection 3.1 if you had difficulty with this question.)
Question E5 (A7)
Explain why the frictional force between two surfaces in contact is (a) independent of the macroscopic area of contact, and (b) dependent on whether the surfaces are slipping or not.
Answer E5
On the microscopic scale the real contact area is much less than on the macroscopic scale. The two surfaces only touch at projection peaks. (a) With a larger macroscopic contact area but the same weight, the number of peaks is greater, but they are less flattened and therefore the frictional forces tend to be about the same. (b) Experimentally the maximum frictional forces before slipping (static friction) always exceed those once slipping has begun (dynamic friction). For this reason the coefficients of static and dynamic friction are unequal.
For a fuller discussion see Subsection 3.3.
Question E6 (A7, A10 and A11)
A body slides down an inclined plane with an acceleration of magnitude 3.55 m s−2. The plane is inclined at an angle of 37° to the horizontal. Determine the coefficient of sliding friction.
Answer E6
Let the mass of the body be m and the frictional force on it, up the plane, have magnitude f. The acceleration is down the plane (taken as the positive x–axis) with no component of acceleration or resultant force perpendicular to the plane (along the positive y–axis). Newton’s second law gives:
along the y–direction: R = mg cos θ
along the x–direction: max = mg sin θ − f
sof = m (g sin θ − ax)
From Equation 15 μslide = f /R = m (g sin θ − ax)/mg cos θ = (g sin θ − ax)/g cos θ
This gives μslide = (9.80 sin 37° − 3.55) m s−2/(9.80 cos 37° m s−2) = 0.30
(Reread Subsection 3.3 if you had difficulty with this question.)
Question E7 (A10 and A11)
Two blocks of masses M and m are coupled by means of a light, inextensible string which passes over a light, frictionless pulley. The block of mass M lies on a horizontal frictionless surface while block of mass m hangs vertically, over the edge of the surface. Find the magnitude of the acceleration of the blocks and the tension in the string when the system is released.
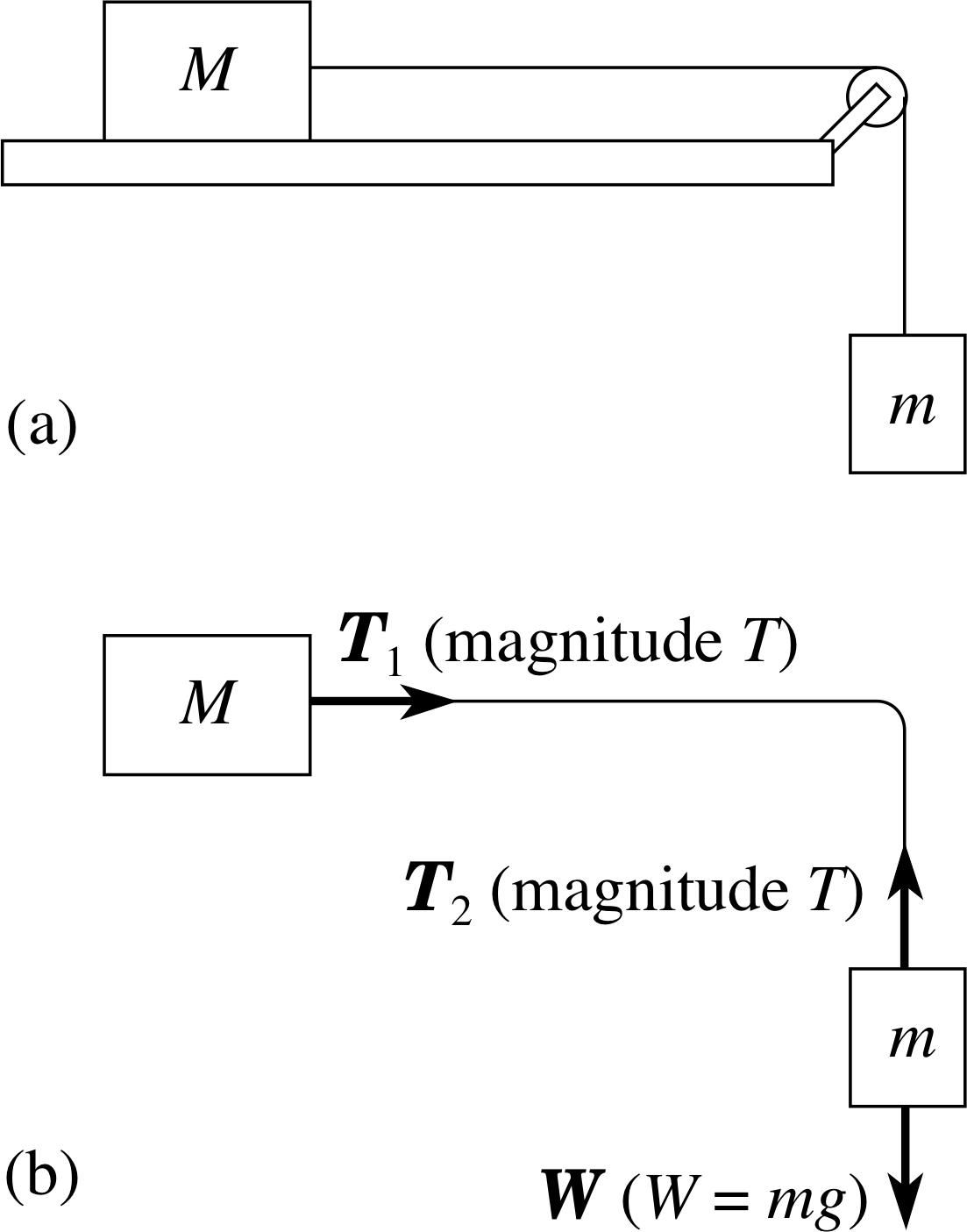
Figure 16 See Answer E7.
Answer E7
Figure 16a illustrates the system described. The string is massless and so the tension is uniform throughout the string. If the string is inextensible, the magnitudes a (but not directions) of the accelerations of the two blocks are equal. If the tension in the string has magnitude T (Figure 16b) we can equate the magnitudes of the two accelerations:
$a = \dfrac TM = \dfrac{mg-T}{m}$
i.e.$g = T\left(\dfrac 1M + \dfrac 1m \right) = T \left(\dfrac{m+M}{mM}\right)$
so$a = \dfrac TM = g\left(\dfrac{m}{m+M}\right)$
We could have arrived at this also by treating the two masses as a total mass of (m + M), subject to a force mg.
The directions of the accelerations should be clear from Figure 16b. The block of mass M accelerates to the right, the block of mass m accelerates vertically downwards.
(Reread Subsection 5.2 if you had difficulty with this question.)
Question E8 (A11)
A particle of mass 0.20 kg, attached to one end of a string of length 0.50 m, is whirled in a circle on a frictionless horizontal surface with gradually increasing speed. Find the maximum speed reached if the string breaks when the tension magnitude reaches a value of 100 N. In which direction does the particle travel after this happens?
Answer E8
Applying Newton’s second law in a radial direction:
mυ2/r = T
where υ is the speed of the particle travelling in a circle of radius r, and T is the tension magnitude in the string, which provides the centripetal acceleration.
If we rearrange this we find
υ = (Tr/m)1/2
and therefore υmax = (100 N × 0.5 m/0.2 kg)1/2 = 15.8 m s−1
The particle moves off tangentially in the direction it was moving at the moment the string broke.
(Reread Subsections 5.3 and 5.4 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 6Closing items.