PHYS 10.4: The Schrödinger equation |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
During the first third of this century a revolution occurred in our perception of the physical laws controlling the behaviour of matter at the atomic level. As a result the rules of classical mechanics, enunciated by Isaac Newton and others, were replaced by the rules of quantum mechanics, in which the Schrödinger equation plays a pivotal role. Newton’s second law can be written as a second–order differential equation and so too can the Schrödinger equation, but the methods of implementation of the new mechanics are radically different from those of the old.
Quantum mechanics is profoundly different from classical mechanics. The behaviour of even the simplest atomic system cannot always be predicted exactly. Often, only a set of probabilities for the allowed values of physical observables such as position, momentum and energy can be predicted. At the heart of the new theory is the idea that a particle’s behaviour is described by a wavefunction Ψ (x, t) which is a complex quantity and which contains all the information we can know about the particle. For a particle in a particular quantum state, it is the corresponding wavefunction that determines the relative likelihood of the various possible outcomes of a measurement. The possible outcomes themselves are determined by a set of eigenvalue equations, each of which features an operator corresponding to one of the observable quantities. The eigenvalue equation for the energy is particularly important. Its solutions reveal both the energy eigenvalues (the possible outcomes of measurements of the energy) and the various energy eigenfunctions that correspond to each of the eigenvalues.
If a particle is in a stationary state, and the spatial part of its wavefunction, ψ (x), is identical to one of these eigenfunctions, then the energy of that particle may be predicted with certainty. It is the eigenvalue equation for energy, more often referred to as the time-independent Schrödinger equation, that will be our main concern in this module.
Section 2 reviews the notion of a de Broglie wave, and introduces the idea of a wavefunction that superceded it. The wavefunction of a free particle is discussed along with the corresponding probability density function and its relation to the Heisenberg uncertainty principle. Section 3 introduces the idea of operators in quantum mechanics and develops differential operators for momentum and kinetic energy in one–dimensional motion. Eigenvalue equations are introduced here, with their associated eigenfunctions and eigenvalues. The eigenvalue equation for kinetic energy then becomes the time-independent Schrödinger equation for a free particle and the solutions of this differential equation are explored. i Techniques are introduced by which information on the position, momentum and energy of a particle can be extracted from its wavefunction. Section 4 discusses the solution of the Schrödinger equation for a particle confined in a one–dimensional box and shows how the use of boundary conditions enables one to explain quantized energy levels in a natural way. In Section 5 the potential energy function is introduced into the Schrödinger equation, and the equation is solved for a region where (a) the total energy exceeds the potential energy and where (b) the total energy is less than the potential energy; the latter case leads to an explanation of barrier penetration and quantum tunnelling. Section 6 provides a brief introduction to the time–independent Schrödinger equation in one dimension.
Physicists today do not say that classical mechanics is wrong and that quantum mechanics is right. Instead, they say that classical mechanics is an approximation and, in fact, quantum mechanics usually becomes identical to it for systems much larger than the atom. In atomic physics, quantum mechanics is all they have and they have to make the best of it! It is a very interesting theory, mathematically challenging of course, but well worth the effort in mastering the elements. In the early days the best physicists in the world, Albert Einstein, Niels Bohr, Max Born and many others spent endless hours arguing about the meaning of quantum mechanics at a deep philosophical level. A total consensus view was definitely not reached. The arguments still rage with undiminished ferocity. Feel free to join in!
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? section.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 7.1Module summary and the Subsection 7.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 7.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Write down the time–independent Schrödinger equation for a free particle of mass m moving in one dimension. Show that the spatial wavefunction ψ (x) = A sin(kx) is a solution of this Schrödinger equation when the potential energy is zero. What is the energy of a particle in a stationary state with this spatial wavefunction? What is the corresponding time–dependent wavefunction Ψ (x, t)?
Answer F1
The time–independent Schrödinger equation is:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$
For a free particle U (x) = 0, and this becomes
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = E\psi(x)$
Substitution of the spatial wavefunction ψ (x) = A sin(kx) gives us:
$\dfrac{-\hbar^2}{2m\os}(-k^2)\psi(x) = E\psi(x)$
which is satisfied if $E = \dfrac{\hbar^2k^2}{2m}$
The corresponding time–dependent wavefunction is ${\it\Psi}\,(x,\,t) = A\sin(kx)\exp\left(\dfrac{-iEt}{\hbar}\right)$
Question F2
Write down an operator for the x–component of momentum. Show that the function ψ (x) = A exp(ikx), with k real, is an eigenfunction of this momentum operator. If a particle has this spatial wavefunction, what would be the result of a measurement of (a) its momentum px or (b) its position?
Answer F2
The operator for the x–component of momentum is $\hat{p}_x = -i\hbar\dfrac{d}{dx}$.
Operating on the spatial wavefunction ψ (x) = A exp(ikx):
$-i\hbar\dfrac{d\psi(x)}{dx} = (-i\hbar)(ik)A\exp(ikx) = \hbar k\psi(x)$
so ψ (x) is an eigenfunction of momentum with eigenvalue $p_x = \hbar k$.
(a) The result of a measurement of momentum must be $p_x = \hbar k$.
(b) The probability of finding the particle in an interval ∆x near x is proportional to | ψ (x) |2∆x = A2 ∆x. A measurement of position gives a result with equal probability anywhere on the x–axis, since | ψ (x) |2 = A2, a constant.
Question F3
Make a sketch of the spatial wavefunction you expect for the lowest energy state of a particle confined in a one–dimensional box of size D. Explain why the kinetic energy cannot be zero. Why must the spatial wavefunction go to zero at the boundaries of the box? Where is the particle most likely to be found when in the lowest energy state?
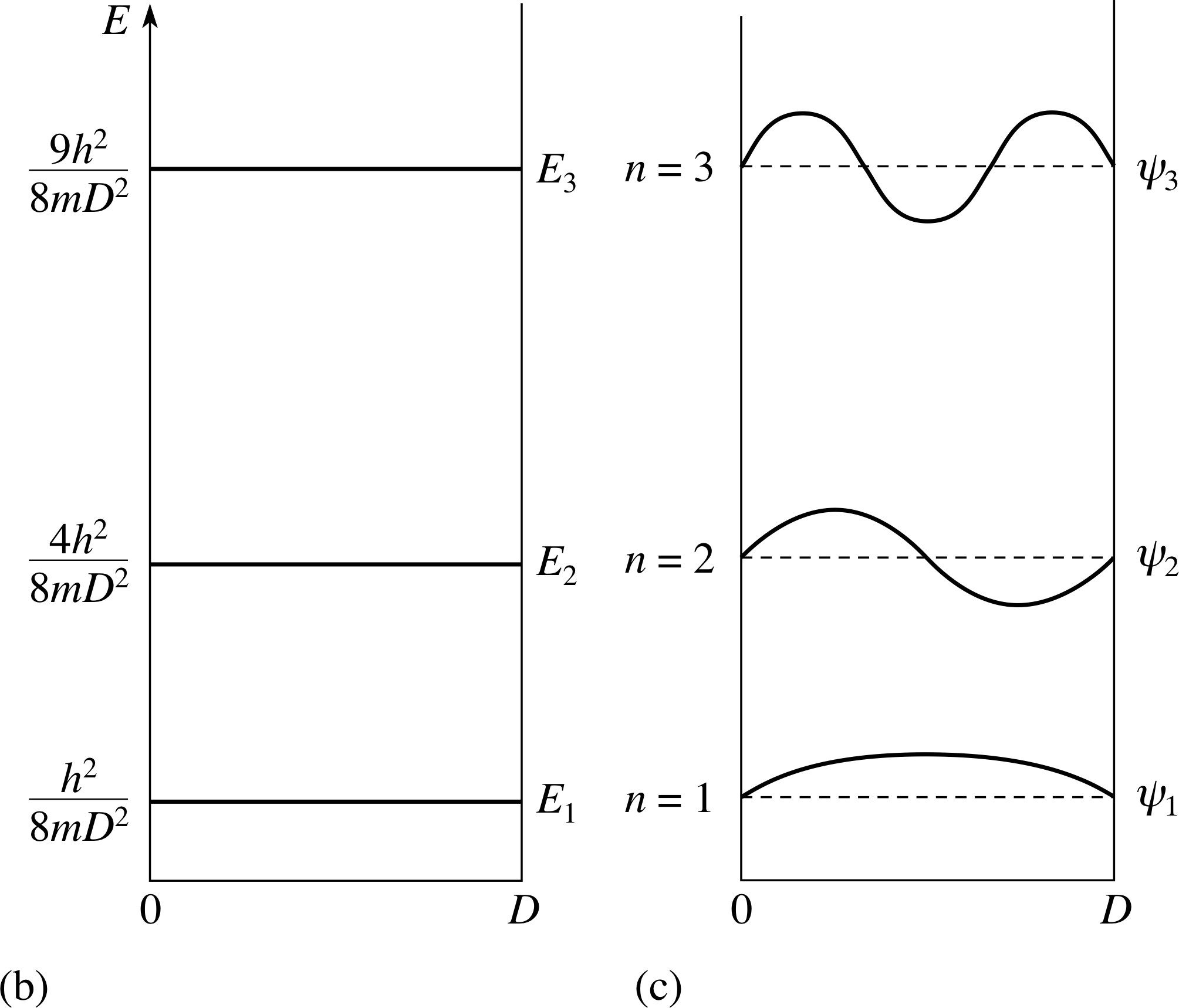
Figure 3b/c (b) The first three energy levels and (c) the corresponding eigenfunctions in this well.
Answer F3
The spatial wavefunction looks like the lowest energy spatial wavefunction ψ1 in Figure 3c.
The allowed energies are given by En = n2h2/(8mD2). If n = 0 then the wavefunction is also zero everywhere (i.e. no particle). The lowest allowed energy is therefore E1 = h2/(8mD2). (This result is also consistent with the Heisenberg uncertainty principle ∆x ∆px).
The spatial wavefunction goes to zero at the boundaries of the box because ψ1(x) = 0 outside the box and the wavefunction is continuous at the boundary. The particle is most likely to be found where the probability density | ψ1(x) |2 is largest. This is at the centre of the box.
Question F4
A particle is moving in a region of constant potential energy V0. Show that the spatial wavefunction A exp(−αx), with α real, is a solution of the time–independent Schrödinger equation when the total particle energy E is less than V0.
Find α in terms of E and V0. Explain whether or not this situation can arise in a world described by classical mechanics.
Answer F4
The time–independent Schrödinger equation in the region may be written:
$\dfrac{\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = (U_0-E)\psi(x)$
Substitution of the spatial wavefunction ψ (x) = A exp(−αx) with α real and positive gives:
$\dfrac{\hbar^2\alpha^2}{2m}\psi(x) = (U_0-E)\psi(x)$
So $\alpha = \dfrac{\sqrt{2m(U_0-E)\os}}{\hbar}$ taking the positive root.
This shows that a particle can penetrate into a region where the total energy E is less than the potential energy U0. This is not possible in a world described by classical mechanics where the kinetic energy, given by (E − U0), is always positive or zero.
1.3 Ready to study?
Study comment In order to study this module you will need to be thoroughly familiar with the treatment of classical waves, including the following physics terms: travelling wave, standing wave, wavelength, angular wavenumber (k = 2π/λ), frequency, angular frequency (ω = 2πf). You should be able to represent a travelling wave in sine or cosine notation. It is also assumed that you are acquainted with the de Broglie hypothesis (λdB = h/p), the Heisenberg uncertainty principle and the Planck–Einstein formula (E = hf). In addition you must be familiar with the basic ideas of classical mechanics, in particular conservation of energy and the potential energy function.
The mathematical requirements of this module are also rather stringent. You must be fully conversant with the idea of a function, the rules of calculuselementary calculus and the meaning of the first and second derivativederivatives of a function. It is also assumed that you are familiar with homogeneous_differential_equationhomogeneous second–order differential equations with constant coefficients and with their general solutions. This is not as scary as it sounds; we will only require differential equations such as that describing the simple harmonic oscillator in mechanics! Of necessity, we have to use complex numbers, so you must be familiar with them in standard cartesian_form_of_a_complex_numberCartesian form z = a + ib, polar_form_of_a_complex_numberpolar form z = A (cos θ + i sin θ) and exponential_form_of_a_complex_numberexponential form z = A exp(iθ) and with the use of Euler’s formula, exp(±iθ) = cos θ ± i sin θ. In particular you will need to know the meaning of the following terms relating to complex numbers: argument_of_a_complex_numberargument, complex conjugate, imaginary part, modulus_of_a_complex_numbermodulus, real part. The following Ready to study questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
(a) What is the momentum px of an electron moving parallel to the positive x–axis with energy 3.5 eV? (1 eV = 1.6 × 10−19 J)
(b) What is the de Broglie wavelength of this electron?
Answer R1
(a) Momentum px = mυx2.
Kinetic energy $E_{\rm kin} = \dfrac{m\upsilon_x^2}{2} = \dfrac{p_x^2}{2m}$
Hence$p_x = \sqrt{2mE_{\rm kin}\os} = \rm \sqrt{2\times9.1\times10^{-31}\,kg\times3.5\times1.6\times10^{-19}\,J\os} = 1.0\times10^{-24}\,kg\,m\,s^{-1}$
(b) The de Broglie wavelength is:
$\lambda_{\rm dB} = \dfrac{h}{p_x} = \rm \dfrac{6.6\times10^{-34}\,J\,s}{1.0\times10^{-24}\,kg\,m\,s^{-1}} = 6.6\times10^{-10}\,m$
Consult momentum, kinetic energy and de Broglie wavelength in the Glossary for further information.
Question R2
Write down an expression for the transverse displacement y (x, t) of a classical wave which is propagating in the positive x–direction with angular wavenumber k and angular frequency ω.
Answer R2
y (x, t) = A cos(kx − ωt) with k = 2π/λ, ω = 2πf.
You may (more generally) have added a phase constant ϕ to the argument kx − ωt, and you may even have used complex notation to write your answer as the real (or imaginary) part of A exp[i (kx − ωt)] where A is complex in the general case.
Consult angular wavenumber and angular frequency in the Glossary for further information.
Question R3
A complex number may be written as z = a + ib where i2 = −1.
(a) Find A and θ if z is written in the form z = A exp(iθ)
(b) Show that A exp[i (θ + π)] = −A exp(iθ)
(c) Show that 2 cos θ = exp(iθ) + exp(−iθ)
Answer R3
(a) $z = a+ib = \sqrt{\smash[b]{a^2+b^2}}(\cos\theta+i\sin\theta) = A\exp(i\theta)$
with$\cos\theta = \dfrac{a}{\sqrt{\smash[b]{a^2+b^2}}}\quad\text{and}\quad\sin\theta = \dfrac{b}{\sqrt{\smash[b]{a^2+b^2}}}$
$A = \dfrac{a}{\sqrt{\smash[b]{a^2+b^2}}}\quad\text{and}\quad\tan\theta = b/a$
(b) A exp[i (θ + π)] = A exp(iθ) exp(iπ) = A exp(iθ)(cos π + i sin π) = −A exp iθ
since cos π = −1 and sin π = 0.
(c) exp(iθ) = cos θ + i sin θ
andexp(−iθ) = cos(−θ) + i sin(−θ) = cos θ − i sin θ
Soexp(iθ) + exp(−iθ) = 2 cosθ + i (sin θ − sin θ) = 2 cosθ
Note that a and b are, respectively, the real_partreal and imaginary_partimaginary parts of z. Also, A is its modulus and θ its argument. Consult complex numbers in the Glossary for further information.
Question R4
If y is the function of the independent variable x given by y = A cos(kx), show that $\dfrac{d^2}{dy^2} = -k^2y$.
Show that this equation is also satisfied by the complex function y = A exp(ikx).
Answer R4
y = A cos(kx) so that:
$\dfrac{dy}{dx} = -kA\sin(kx)\quad\text{and}\quad\dfrac{d^2y}{dy^2} = -k^2A\cos(kx) = -k^2y$
If y = A exp(ikx) then:
$\dfrac{dy}{dx} = Aik\exp(ikx)\quad\text{and}\quad\dfrac{d^2y}{dy^2} = A(ik)^2\exp(ikx) = -k^2y$
Consult derivative in the Glossary for further information.
2 The wavefunction of a free particle
The wavefunction is the central concept of quantum mechanics. This section introduces wavefunctions and explains their significance.
2.1 A free particle represented by a complex travelling wave
Let us imagine a particle, for example an electron or a proton, moving freely through space. There are no forces acting on the particle so it travels in a straight line, say in the x–direction, with constant momentum. If the momentum is px = mυx then in classical physics the kinetic energy is given by:
$E_{\rm kin} = \dfrac12m\upsilon_x^2 = \dfrac{p_x^2}{2m}$(1)
In quantum physics, the associated de Broglie wave has a de Broglie wavelength λdB given by:
de Broglie wavelengthλdB = h/px(2) i
and frequency f given by the
Planck–Einstein formulaE = hf(3)
The transverse displacement y (x, t) of a classical travelling wave propagating in the positive x–direction may be written in terms of the wave amplitude A, the angular wavenumber k = 2π/λ, and the angular frequency ω = 2πf as:
y (x, t) = A cos(kx − ωt) i
This equation can be written as the real part of a complex quantity:
$y(x,\,t) = {\rm Re}\left\{A\exp\left[i(kx-\omega t)\right]\right\}$ i
For a de Broglie wave travelling in the x–direction, Equations 2 and 3 relate the angular wavenumber and angular frequency to the momentum and the energy, respectively, through the expressions:
$p_x = \hbar k$(4)
and$E = \hbar\omega$(5)
where we have written $\hbar = h/(2\pi)$ i
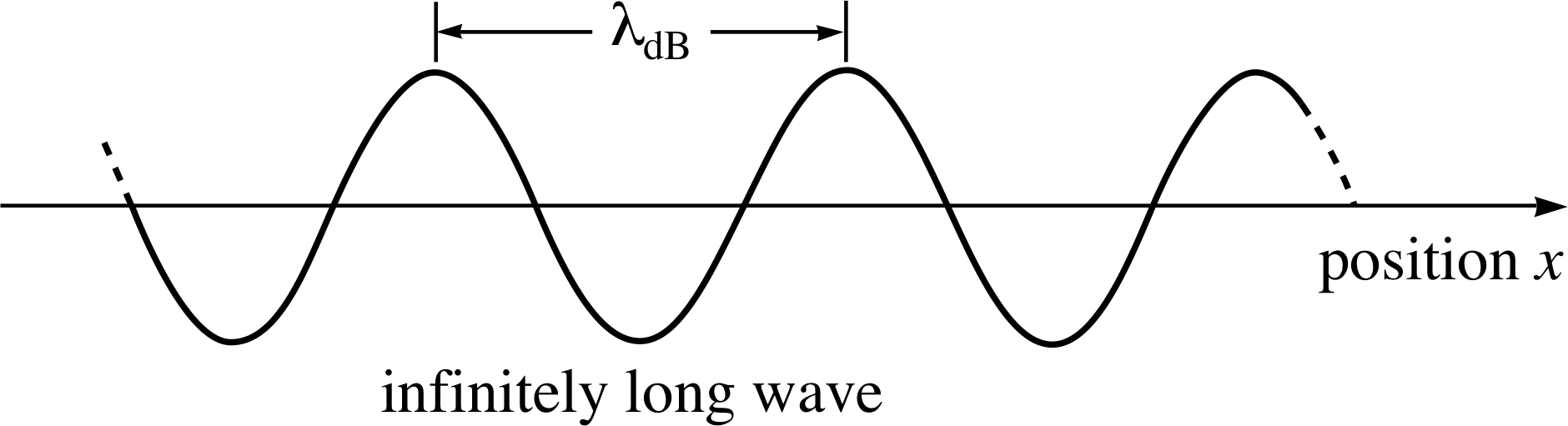
Figure 1 An infinitely long de Broglie wave of fixed amplitude. The wavelength gives the momentum exactly but we can know nothing of the particle’s position coordinate.
Thus the de Broglie wave may be written
${\rm Re}\left\{A\exp\left[i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right]\right\}$
The wave is shown in Figure 1.
We will see that in quantum mechanics the wavefunction,Ψ (x, t), used to describe a free particle moving with definite momentum, has to be a complex quantity, not merely the real part of such a quantity. In this case we can say:
The wavefunction of a free particle with momentum px and energy E is
${\it\Psi}\,(x,\,t) = A\exp\left[i(kx-\omega t)\right] = A\exp\left[i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right]$(6) i
where A is a complex constant.
A particle with a wavefunction in the form of Equation 6 has a definite momentum px and a definite total energy E. A ‘snapshot’ of the real part of the wavefunction at a particular time would look like the de Broglie wave of Figure 1. However the full quantum mechanical wavefunction is a complex quantity and cannot be depicted in such a simple way.
The formal association between the wavefunction and the probability of finding the particle in a given small region around the point x at time t is given as follows:
The probability of finding the particle within the small interval ∆x
around the position x at time t is proportional to | Ψ (x, t) |2 ∆x(7)
This formal association with probability was due to Max Born and has become known as the Born probability hypothesis. i Notice the following points here:
- Since | Ψ (x, t) | is a real quantity (it doesn’t involve i), it must be the case that | Ψ (x, t) |2 is positive. It is therefore at least possible that | Ψ (x, t) |2 might represent a probability, since probabilities are represented by real numbers in the range 0 to 1 with 0 for no possibility and 1 for certainty.
- Since ∆x is taken to be very small, | Ψ (x, t) |2 can be thought of as the probability per unit length, or probability density around position x. i
- | Ψ (x, t) |2 ∆x is a statistical indicator of behaviour. Given a large number of experiments to measure the position of a particle, set up under identical conditions, it represents the fraction of those experiments that will indicate a particle in the range ∆x at a time t. The set up for the experiment is fixed but the results of individual experiments are not always the same.
- We may usually convert the proportionality in Equation 7 into an equality, provided we choose an appropriate scale of probability. i For the moment, we do not need to be concerned with this refinement, but we will return to it in Subsection 4.2 when we discuss normalization.
Let us now calculate the probability density function corresponding to the wavefunction of Equation 6,
${\it\Psi}\,(x,\,t) = A\exp\left[i(kx-\omega t)\right] = A\exp\left[i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right]$(Eqn 6)
The square of the modulus of the wavefunction is found from the product of the wavefunction Ψ (x, t) and its complex conjugate, Ψ*(x, t): i
i.e.| Ψ (x, t) |2 = Ψ*(x, t) Ψ (x, t)(8)
Here$\lvert\,{\it\Psi}\,(x,\,t)\,\rvert^2 = A^*\exp\left[-i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right] \times A\exp\left[i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right] = A^2$
The probability of finding the particle described by Equation 6 is therefore the same everywhere, irrespective of the x–coordinate! Although this wavefunction gives precise information on momentum it tells us nothing about the position of the particle in space. This is a very important lesson; when the wavefunction tells us exactly what the particle’s momentum is, then it tells us nothing about its position. i
2.2 A free particle represented by a complex wave packet

Figure 2 A wave packet formed by a superposition of eight waves of different amplitudes and wavelengths.
The wavefunction of a free particle whose position is at least approximately known may be represented by a wave packet or wave group (Figure 2) consisting of a superposition of complex waves with a limited but continuous range of angular wavenumbers, rather than a single wave. The probability density is then no longer independent of position, but rather peaks around the mean position of the particle. i
Such a wavefunction corresponds to a superposition of a continuous range of possible momenta for the associated particle, and we find that the position and momentum uncertainties are coupled through the Heisenberg uncertainty principle,
$\Delta x\,\Delta p_x \gtrsim \hbar$
The speed with which a classical wave packet travels is not determined by the phase speed υϕ = ω/k of the individual waves but by the group speed υg = dω/dk. i So, we can calculate the group speed if we know the relation between ω and k. This relationship is known as the dispersion relation.
For a wave_packetquantum wave packet the dispersion relation can be found from Equations 1, 4 and 5.
$E_{\rm kin} = \dfrac12m\upsilon_x^2 = \dfrac{p_x^2}{2m}$(Eqn 1)
$p_x = \hbar k$(Eqn 4)
and$E = \hbar\omega$(Eqn 5)
For a free particle we may define the potential energy to be zero, the total energy E is then equal to the kinetic energy, p2/2m, and we may write
$E = \hbar\omega = \dfrac{p^2}{2m} =\dfrac{\hbar^2k^2}{2m}\quad\text{so}\quad\omega = \dfrac{\hbar k^2}{2m}$
Thus, the phase speed is
$\upsilon_\phi = \dfrac{\omega}{k} = \dfrac{\hbar k}{2m} = \dfrac{p}{2m} = \dfrac{\upsilon}{2}$
and the group speed is
$\upsilon_{\rm g} = \dfrac{d\omega}{dk} = \dfrac{d}{dk}\left(\dfrac{\hbar k^2}{2m}\right) = \dfrac{\hbar k}{m} = \dfrac{p}{m} = \upsilon$
Note By choosing the potential energy to have some constant value other than zero we would change the phase speed (thus showing its lack of direct physical significance) but not the group speed.
For a quantum wave packet, the group speed with which the packet moves (which is the speed with which the energy is transmitted) is equal to the speed of the associated particle. This is reassuring!
Question T1
A particle moves in one dimension and is described by the wavefunction Ψ (x,t) = A exp[i (ax − bt)], where a and b are positive real constants. Write down expressions for the momentum px of the particle and for the energy of the particle.
Answer T1
The general expression in Equation 6,
${\it\Psi}\,(x,\,t) = A\exp\left[i(kx-\omega t)\right] = A\exp\left[i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right]$(Eqn 6)
for which Equations 4 and 5,
$p_x = \hbar k$(Eqn 4)
$E = \hbar\omega$Eqn (5)
give $p_x = \hbar k$ and $E = \hbar\omega$, shows that the momentum and energy can be found from the coefficients of x and t, respectively, in the exponent. By comparison with Ψ (x, t) = A exp[i (ax − bt)] we find k = a and ω = b, so the momentum $p_x = \hbar a$ and the energy $E = \hbar b$.
Question T2
For the particle described by the wavefunction in Question T1, write down an expression for the probability density function. Is this result consistent with the Heisenberg uncertainty principle?
Answer T2
Equation 8 gives | Ψ (x, t) |2 = Ψ*(x, t)Ψ (x, t)
So|Ψ (x,t) |2 = A exp[−i (ax − bt)] × A exp[i (ax − bt)] = A2
This function is independent of position, so the particle could be anywhere. However the momentum is known precisely, in terms of the constant a, as we saw in the answer to Question T1. This is an example of the Heisenberg uncertainty principle at work.
3 From Newton to Schrödinger
The fundamental statement of classical mechanics is embodied in Newton’s second law of motion. In one dimension this can be written as:
Newton’s second law: $F_x(t) = m\dfrac{d^2x(t)}{dx^2}$(9)
There are two extremely important aspects of Equation 9:
- This second–order differential equation plays the central predictive role in classical physics; it gives the time evolution of the position x (t) of the particle, when acted on by a force Fx(t). If we are told some initial conditions and also the force acting on the particle at all times then we can predict its position, velocity and acceleration at any later time.
- It is vital to appreciate that Equation 9 cannot be proved mathematically – it is an equation which is used to derive almost all of the equations of mechanics but its own veracity rests not on mathematics but on experimental observations. We believe it because it works!
Equation 6,
${\it\Psi}\,(x,\,t) = A\exp\left[i(kx-\omega t)\right] = A\exp\left[i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right]$(Eqn 6)
provides us with an example of a complex wavefunction. We have introduced it as though it were simply a generalized de Broglie wave, representing a very simple situation – a particle with a definite momentum and energy. However, the truth of the matter is that the wavefunction is found by solving a differential equation. In what follows we will use the wavefunction of Equation 6 to launch an investigation into the nature of that differential equation. This will not be a rigorous mathematical process, but it will lead to an equation that plays a pivotal role in quantum mechanics, just as Equation 9 does in classical mechanics. The aim then is to find a differential equation, the Schrödinger equation, whose solutions include our simple waves but whose general solutions are the wavefunctions which describe any system for which we may have to make predictions. This is an ambitious target, but not beyond our reach. We will begin the quest by exploring the time dependence of our simple wavefunction.
3.1 The time dependence of the wavefunction and stationary states
The wavefunction for a particle with energy E and momentum px may be written in the complex form:
${\it\Psi}\,(x,\,t) = A\exp\left[i(kx-\omega t)\right] = A\exp\left[i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right]$(Eqn 6)
Since ea+b = ea × eb, Equation 6 can be separated into two parts, the first $[A\exp(ip_xx/\hbar)]$ depending on position and the second $[\exp(-iEt/\hbar)]$ depending on time. We will now generalize this particular result by stating that the time–dependent part of any wavefunction that describes a particle moving in one dimension with a definite total energy E may be written $\exp(-iEt/\hbar)$. Hence:
In one dimension the wavefunction of any particle with definite total energy E is given by:
${\it\Psi}\,(x,\,t) = \psi(x)\exp\left(-\dfrac{iE}{\hbar}t\right)$(10)
where ψ (x) in Equation 10 is called the space–dependent part of the wavefunction or simply the spatial wavefunction. i ψ (x) can have many forms and it will be our business to study some of them in various physical situations. We will give further justification to this claim in Section 6.
We can re–examine the probability density function (Equation 8),
| Ψ (x, t) |2 = Ψ*(x, t) Ψ (x, t)(Eqn 8)
for the case of the general wavefunction of Equation 10. We see that the time dependence in | Ψ (x, t) |2 disappears whenever the wavefunction corresponds to a fixed energy. The probability density P (x) depends on position but not time, and for this reason the wavefunctions for states of a fixed energy are known as stationary states. The free particle wavefunction of Equation 6 is an example of a stationary state wavefunction.
From now on we will be primarily concerned with particles of definite total energy moving in one dimension, so their wavefunctions will describe stationary states and will take the form shown in Equation 10.
Consequently, we will not need to consider the time–dependent parts of these wavefunctions, since they are automatically determined once the relevant value of the energy is known. Instead we will concentrate on the spatial part of the wavefunction, ψ (x), and the corresponding energy E. Our task of finding the quantum mechanical equivalent of Newton’s second law – the differential equation that determines wavefunctions – has now been reduced to the following:
What is the differential equation that determines the spatial part of a stationary state wavefunction of fixed energy E?
The differential equation we are now searching for is called the time-independent Schrödinger equation. As a first step towards uncovering its nature we need to consider in greater detail the way in which the wavefunction provides information about the measurable properties such as energy and momentum.
3.2 Introducing operators – an operator for momentum
The wavefunction contains all that we can hope to know about the quantum state of a system. But how are we to obtain that information? For the free particle wavefunction of Equation 6,
${\it\Psi}\,(x,\,t) = A\exp\left[i(kx-\omega t)\right] = A\exp\left[i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right]$(Eqn 6)
we have already established that the time dependence of the wavefunction is determined by the energy, whereas the spatial dependence is determined by the momentum. This suggests that to determine the energy from the wavefunction we should look at its time dependence and to find the momentum we should look at its spatial dependence, that is, its x–dependence for one–dimensional motion.
Let us formalize this a little more by first taking the derivative of our special spatial wavefunction, $\psi(x) = A\exp\left(\dfrac{ip_x}{\hbar}x\right)$, with respect to x, thus finding out how the spatial wavefunction for a particle moving freely along the x–axis changes with x.
If$\psi(x) = A\exp\left(\dfrac{ip_x}{\hbar}x\right)$(11)
then$\dfrac{d\psi(x)}{dx} = \left(\dfrac{ip_x}{\hbar}\right)A\exp\left(\dfrac{ip_x}{\hbar}x\right) = \left(\dfrac{ip_x}{\hbar}\right)\psi(x)$
Multiplying both sides of this equation by $-i\hbar$ we may write it as follows:
$\left[-i\hbar\dfrac{d}{dx}\right]\psi(x) = p_x\psi(x)$(12)
Equation 12 is an example of a very important class of mathematical equations known as eigenvalue equations.
In an eigenvalue equation, some mathematical operation is carried out on a function appearing on the left–hand side of the equation with the result that the same function reappears multiplied by a real number on the right–hand side.
The mathematical operation occurring on the left of an eigenvalue equation can be anything from simply ‘multiply by a number’ or ‘take the sine, cosine or logarithm’ to, as here, ‘take the derivative with respect to x and then multiply by $-i\hbar$’. The operation is said to be carried out by an operator. The expression $-i\hbar\dfrac{d}{dx}$ is an example of a differential operator.
When an eigenvalue equation is satisfied then a function which is a solution is called an eigenfunction and the real number which is generated as a multiplier is said to be the corresponding eigenvalue. i In Equation 12 the differential operator $-i\hbar\dfrac{d}{dx}$ is the momentum operator; the eigenfunction is the spatial wavefunction of Equation 11,
$\psi(x) = A\exp\left(\dfrac{ip_x}{\hbar}x\right)$(Eqn 11)
and the eigenvalue is the corresponding value of the momentum px.
Physical quantities which have eigenvalues are called observables in quantum mechanics.
In the mathematical language of quantum mechanics we say that this spatial wavefunction is an eigenfunction of the momentum operator, or more simply, an eigenfunction of momentum. The momentum value is an eigenvalue of the equation and so the problem of finding the possible values for the momentum of the particle becomes the problem of finding the functions which are the eigenfunctions of the momentum operator and then finding the eigenvalues.
There is a general problem in solving an eigenvalue equation in that both the eigenfunctions and the eigenvalues are unknown initially. Very often a solution is found by recognizing the eigenvalue equation as a differential equation whose general solutions are known and then inferring the general form of the physical eigenfunctions from the physical form of the solutions required – by inspiration in fact!
We now adopt Equation 12,
$\left[-i\hbar\dfrac{d}{dx}\right]\psi(x) = p_x\psi(x)$(Eqn 12)
as a law of quantum mechanics which applies in all circumstances where the particle has a defined momentum, not just for the single travelling wave solution.
So:
The operator corresponding to the x–component of momentum, denoted $\hat{\rm p}_x$ is always expressible as:
$\hat{\rm p}_x = -i\hbar\dfrac{d}{dx}$(13) i
A function ψ (x) will be an eigenfunction of momentum, with eigenvalue px if it satisfies
$\hat{\rm p}_x\psi(x) = p_x\psi(x)$(14) i
The free particle spatial wavefunction
$\psi(x) = A\exp\left(\dfrac{ip_xx}{\hbar}\right)$
meets this requirement and is therefore an eigenfunction of momentum with eigenvalue px.
Question T3
Which of the following functions are eigenfunctions of momentum and what are the corresponding eigenvalues, if any? In each case q is a positive real number.
(a) $\psi(x) = A\exp\left(\dfrac{iqx}{\hbar}\right)$, (b) $\psi(x) = A\exp\left(\dfrac{qx}{\hbar}\right)$, (c) $\psi(x) = A\exp\left(\dfrac{-iqx}{\hbar}\right)$.
Answer T3
In each case the simple test is to apply the momentum operator to each function.
If the result is a real number × the original function, then the function is an eigenfunction and the real number is the momentum eigenvalue.
(a) $-i\hbar\dfrac{d\psi(x)}{dx} = -i\hbar\left(\dfrac{iq}{\hbar}\right)\exp\left(\dfrac{iqx}{\hbar}\right) = q\psi(x)$
The function is an eigenfunction of momentum and the eigenvalue is q.
(b) $-i\hbar\dfrac{d\psi(x)}{dx} = -i\hbar\left(\dfrac{q}{\hbar}\right)\left[-\sin\left(\dfrac{qx}{\hbar}\right)\right] = iq\sin\left(\dfrac{qx}{\hbar}\right) \ne \text{real number}\times\psi(x)$
This function is not an eigenfunction of momentum.
(c) This function is an eigenfunction of momentum, the proof follows exactly as in case (a) and the eigenvalue is −q.
Application of the momentum operator to a wavefunction is the mathematical equivalent of making a measurement of the particle’s momentum. If the wavefunction of a system is an eigenfunction of the momentum operator then the result of measuring the momentum of the system will be the corresponding momentum eigenvalue. This corresponds to the result of a physical measurement giving a definite, predictable value of the momentum – if the momentum eigenvalue is px then the result of a measurement of momentum is definitely px.
If, however, the wavefunction involves a combination of momentum eigenfunctions then it will not be an eigenfunction of momentum. The result of a momentum measurement may then be any one of the eigenvalues corresponding to the eigenfunctions involved in the combination. In this case the wavefunction may be used to predict the relative likelihood (i.e. the probability) of each of the possible outcomes. i
3.3 An operator for kinetic energy
The general strategy for obtaining observable properties of the system in quantum mechanics is to discover the appropriate operator and to write down and solve the eigenvalue equation involving this operator. This may seem an odd approach at first, because it is quite different from that used in classical physics. Nevertheless, let us press on and try to anticipate a suitable operator for another important observable – the kinetic energy. i
We will be guided by the result from classical physics – that in one–dimensional motion the kinetic energy is expressible in terms of the momentum as Ekin = px2/(2m). It is natural then to construct an operator for kinetic energy by replacing px in this expression by the operator $\hat{\rm p}_x = -i\hbar\dfrac{d}{dx}$. This implies that we should apply the momentum operator twice to the spatial wavefunction of Equation 11,
$\psi(x) = A\exp\left(\dfrac{ip_x}{\hbar}x\right)$(Eqn 11)
then dividing the result by 2m to find the kinetic energy as an eigenvalue. Let us try it!
Operating once with $\hat{\rm p}_x$:$-i\hbar\dfrac{d\psi(x)}{dx} = p_x\psi(x)$(Eqn 12)
Operating twice:$-i\hbar\dfrac{d\psi}{dx}\left(-i\hbar\dfrac{d\psi}{dx}\right) = -ih\dfrac{d}{dx}\left[p_x\psi(x)\right]$
but, remember that:$-i\hbar\dfrac{d\psi}{dx}\left(-i\hbar\dfrac{d\psi}{dx}\right) = -\hbar^2\dfrac{d^2\psi(x)}{dx^2}$
and, as px is constant:$-ih\dfrac{d}{dx}\left[p_x\psi(x)\right] = p_x\left(-i\hbar\dfrac{d}{dx}\psi(x)\right) = p^2x\dfrac{d^2\psi(x)}{dx^2}$
Thus:$-\hbar^2\dfrac{d^2\psi(x)}{dx^2} = p_x^2\psi(x)\quad\text{i.e.}\quad\left[-\hbar^2\dfrac{d^2}{dx^2}\right]\psi(x) = p_x^2\psi(x)$
Dividing both sides of this equation by 2m we produce another eigenvalue equation, with the kinetic energy appearing as an eigenvalue on the right. We may therefore identify the operator on the left as the kinetic energy operator.
Again, we will assume that this result, valid for the special case of a free particle wavefunction, is also valid generally. We can the summarize as follows:
The operator corresponding to the kinetic energy in one–dimensional motion is always expressible as:
$\hat{\rm E}_{\rm kin} = \dfrac{-\hbar^2}{2m\os}\dfrac{d^2}{dx^2}$(15)
with:$\hat{\rm E}_{\rm kin}\psi(x) = E_{\rm kin}\psi(x)$(16)
The free particle spatial wavefunction
$\psi(x) = A\exp\left(\dfrac{ip_xx}{\hbar}\right)$
meets this requirement and is therefore an eigenfunction of kinetic energy with eigenvalue Ekin = px2/(2m).
Question T4
Show that the function $\psi(x) = A\cos\left(qx/\hbar\right)$ is an eigenfunction of kinetic energy. What is the corresponding eigenvalue?
Answer T4
We have already shown in Question T3 that this function is not an eigenfunction of momentum. However it is an eigenfunction of kinetic energy, as can be seen by applying the kinetic energy operator:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2}{dx^2}\left[A\cos\left(\dfrac{qx}{\hbar}\right)\right] = \dfrac{-\hbar^2}{2m\os}\left(\dfrac{-q^2}{\hbar^2}\right)A\cos\left(\dfrac{qx}{\hbar}\right) = \dfrac{q^2}{2m\os}\psi(x)$
The result is a real number × the function. The spatial wavefunction therefore corresponds to a particle of mass m with kinetic energy q2/2m. We shall discuss spatial wavefunctions such as this in Subsection 3.5.
3.4 The free particle time–independent Schrödinger equation
Now we have all the tools necessary to reach our first goal – establishing the form of the time–independent Schrödinger equation for the free particle. Remember, the role of the time–independent Schrödinger equation was to determine the spatial part of a wavefunction of fixed energy E. We can now express this by saying:
The time–independent Schrödinger equation for any system is simply the eigenvalue equation for the total energy of the system. i
Our task here is to discover an operator for the total energy of our free particle and then to write down a differential equation which is an eigenvalue equation of the total energy operator. The result must be consistent with the fact that the free particle spatial wavefunction, $\psi(x) = A\exp\left(\dfrac{ip_xx}{\hbar}\right)$, corresponding to a fixed total energy, must therefore be an eigenfunction of the total energy operator.
Fortunately this task is fairly straightforward. As we noted earlier, the potential energy of a free particle is constant and may be chosen to be zero. If we make this choice, the total energy of the free particle is identical to its kinetic energy, and the kinetic energy operator of Equation 15,
$\hat{\rm E}_{\rm kin} = \dfrac{-\hbar^2}{2m\os}\dfrac{d^2}{dx^2}$(Eqn 15)
is also the total energy operator. We can therefore say that:
The time-independent Schrödinger equation for a free particle moving in one dimension is:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = E\psi(x)$(17) i
Notice that we have not derived this second–order differential equation from anything. Schrödinger did not derive it either! He stated it as a rule of quantum mechanics, which could be justified only by the critical comparison of its predictions with experimental results. This is also entirely in keeping with the role played by Newton’s second law in classical physics, as we discussed in Subsection 2.2.
In obtaining Equation 17 we have adopted an approach based on inspiration and the fore–knowledge of the wavefunction for a free particle.
Of course, quantum mechanics must be applicable in much more complicated situations, where we may have no idea of the form of the wavefunctions or the energies. To deal with such situations we will need a more general form of the time–independent Schrödinger equation, one that is not limited to free particles. However, before we try to develop such an equation let us pause to investigate Equation 17.
3.5 Solving the free particle Schrödinger equation
For a fixed value of E, Equation 17,
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = E\psi(x)$(Eqn 17)
is a linear_second_order_differential_equationlinear homogeneous second–order differential equation with constant coefficients and its general solution has the standard form:
ψ (x) = A exp(ikx) + B exp(−ikx)(18) i
where A and B are arbitrary complex constants and the constant k relates to the constant E through the expression:
$E = \dfrac{\hbar^2k^2}{2m}$(19)
Question T5
Verify, by direct substitution, that Equation 18 is a solution to the free particle Schrödinger equation (Equation 17).
Answer T5
We need to find the second derivative of ψ (x) and substitute this into the time–independent Schrödinger equation.
If$\psi(x) = A\exp(ikx) + B\exp(-ikx)$
then$\dfrac{d\psi(x)}{dx} = ikA\exp(ikx) - ikB\exp(-ikx)$
and$\dfrac{d^2\psi(x)}{dx^2} = -k^2A\exp(ikx) - k^B\exp(-ikx) = -k^2\psi(x)$
Substituting this into the Schrödinger equation:
$\dfrac{-\hbar^2}{2m}(-k^2)\psi(x) = E\psi(x)$
This is satisfied if $E = \dfrac{\hbar^2k^2}{(2m)}$.
Question T6
Show that the function ψ (x) = A exp(ikx) is an eigenfunction of momentum with eigenvalue $p_x = \hbar k$ and an eigenfunction of kinetic energy with eigenvalue $E_{|rm kin} = \hbar^2k^2/(2m)$.
Answer T6
Applying the momentum operator $\hat{\rm p}_x = -i\hbar\dfrac{d}{dx}$ to ψ (x):
$-i\hbar\dfrac{d\psi(x)}{dx} = -i\hbar(ik)A\exp(ikx) = \hbar k\psi(x)$
The result is a real number × ψ (x); the momentum eigenvalue is $p_x= \hbar k$.
Applying the kinetic energy operator to ψ (x):
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = \dfrac{-\hbar^2}{2m\os}(ik)^2A\exp(ikx) = \dfrac{\hbar^2k^2}{2m\os}\psi(x)$
The result is a real number × ψ (x); the kinetic energy eigenvalue is $\hbar^2k^2/(2m)$. As expected, the kinetic energy Ekin is also given by px2/(2m).
In the special case where B = 0 in Equation 18, ψ (x) becomes the spatial wavefunction of a free particle moving with definite momentum $p_x = \hbar k$ in the positive x–direction and having a total energy E = px2/(2m). Alternatively, if A = 0, ψ (x) becomes the spatial wavefunction of a particle with the same total energy but with momentum $p_x = -\hbar k$, so it is moving in the negative x–direction.
A most interesting case arises when A = B in Equation 18. We can then write:
ψ (x) = A [exp(ikx) + exp(−ikx)]
We can use Euler’s relation, that exp(±iθ) = cos θ ± i sin θ, to write: i
ψ (x) = A [cos(kx) + i sin(kx) + cos(−kx) + i sin(−kx)]
soψ (x) = A [2 cos(kx) + i (sin(kx) − sin(kx))] = 2A cos(kx)
This spatial wavefunction is an eigenfunction of kinetic energy but it is not an eigenfunction of momentum, as we saw in the answer to part b of Question T3. The mathematics shows that the spatial wavefunction is the sum of two parts. The first part, exp(ikx), is itself an eigenfunction of momentum and represents a particle with definite momentum $p_x = \hbar k$. The second part, exp(−ikx), is another momentum eigenfunction corresponding to momentum $p_x = -\hbar k$.
This situation is interpreted in the following way. If a particle has wavefunction proportional to cos(kx) then a measurement of momentum is equally likely to give $p_x = \hbar k$ or $p_x = -\hbar k$. The particle is equally likely to be moving in the positive or negative directions. i This is typical of the superposed states that can arise in quantum physics. We often have to accept that we cannot make definite predictions about the state of motion or the position of a particle. When this occurs the best we can do is to predict the probability of the possible outcomes of a measurement.
Contrast this situation with that described by Newtonian mechanics. In the large scale world, if a particle is free to move in the x–direction its position and momentum can both be known simultaneously and we can follow the particle’s trajectory. In the quantum world the concept of a trajectory is lost. For example, you may have noticed that we set up the previous problem by saying that the particle had only x–motion (i.e. motion parallel to the x–axis) but not that it was moving along the x–axis. To have only x–motion requires that py = pz = 0, so that the y– and z–momenta are known perfectly; the claim that the motion was along the x–axis would also require y = 0 and z = 0, i.e. perfect knowledge of the y and z position coordinates. To claim such perfect knowledge of both position and momentum along either of these two axes is a violation of the Heisenberg uncertainty principle. To be confident of having one–dimensional x–motion requires complete ignorance of the y and z position coordinates, so the particle cannot be said to be moving along the x–axis.
Question T7
Show that the spatial wavefunction ψ (x) = A sin(kx) is a solution of the free particle time–independent Schrödinger equation (Equation 17).
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = E\psi(x)$(Eqn 17)
What is the kinetic energy of the associated particle? What are the possible results of a measurement of momentum?
[Hint: Express sin(kx) as a sum of two exponential terms.]
Answer T7
Using ψ (x) = A sin(kx):
$\dfrac{d\psi(x)}{dx} = Ak\cos(kx)$
and $\dfrac{d^2\psi(x)}{dx^2} = -Ak^2\sin(kx) = -k^2\psi(x)$
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = E\psi(x)$(Eqn 17)
gives:
$\dfrac{-\hbar^2}{2m}\left[-k^2\psi(x)\right] = E\psi(x)$
This is satisfied if the total energy $E = \dfrac{\hbar^2k^2}{(2m)}$.
Since the potential energy is zero, $E = E_{\rm kin} = \dfrac{\hbar^2k^2}{(2m)}$.
This spatial wavefunction is not an eigenfunction of momentum, as we can check by operating with the momentum operator:
$-i\hbar\dfrac{d\psi(x)}{dx} = -i\hbar k\cos(kx) \ne \text{(real number)}\times\psi(x)$
However, we can use Euler’s relation to express ψ (x) = A sin(kx) as the sum of two complex functions, each of which is a momentum eigenfunction:
$\psi(x) = A\sin(kx) = A\left[\dfrac{\exp(ikx) - \exp(-ikx)}{2}\right] = \dfrac{A}{2i}\exp(ikx) - \dfrac{A}{2i}\exp(-ikx) \\ \phantom{\psi(x) = A\sin(kx) }= \dfrac{A}{2i}\left[\exp\left(\dfrac{i(\hbar k)x}{\hbar}\right) - \exp\left(\dfrac{i(-\hbar k)x}{\hbar}\right)\right]$
A measurement of momentum is thus equally likely to give the result $p_x = \hbar k$ or $p_x = -\hbar k$.
Question T8
The spatial wavefunction ψ (x) = A cos(kx) is one possible solution of the free particle time–independent Schrödinger equation (Equation 17).
Write down the corresponding probability density P (x) = | ψ (x) |2 and sketch both ψ (x) and P (x) from x = −π/k to x = +π/k. Where is the particle most likely to be found within this range and where is it least likely to be found?
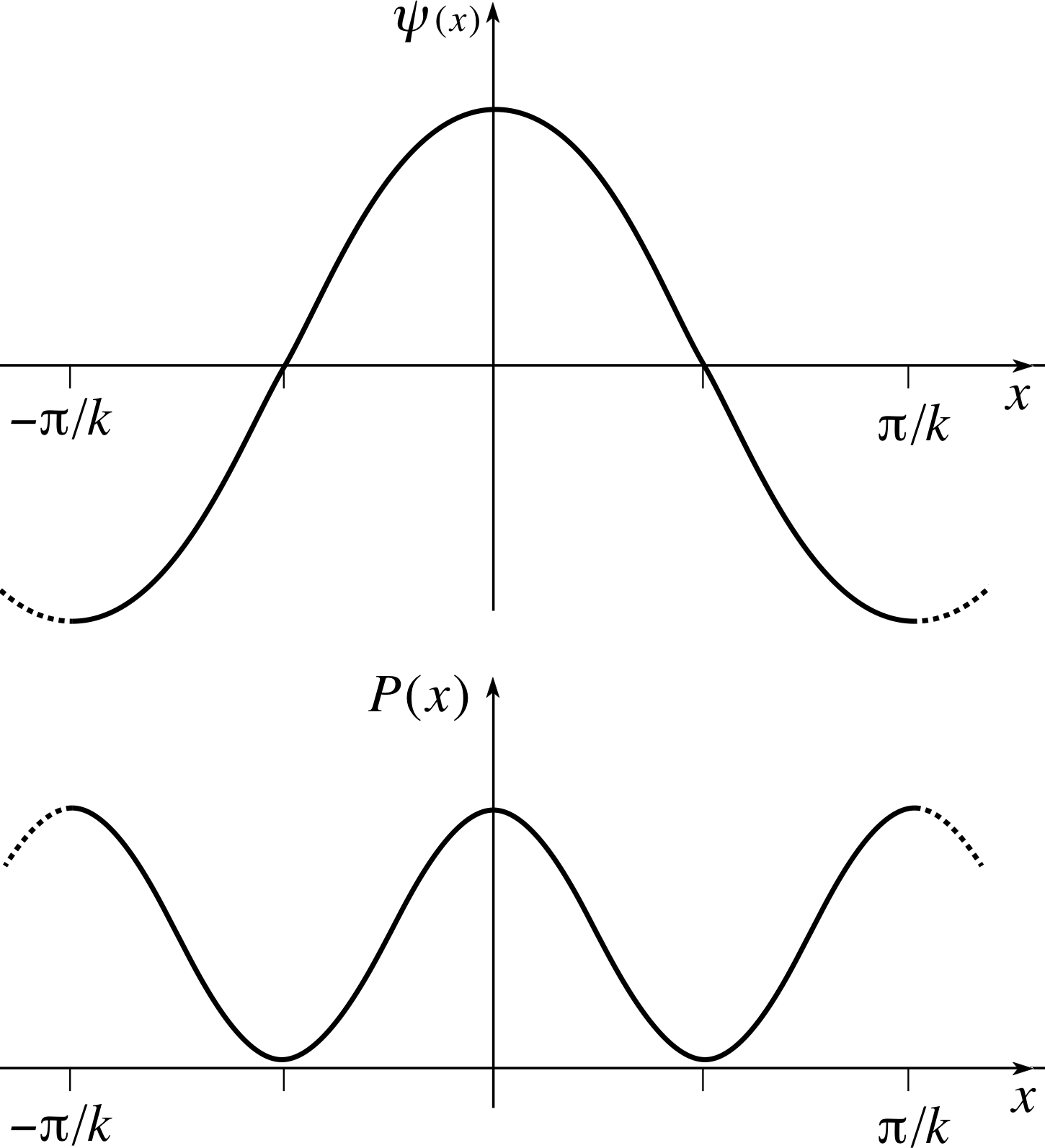
Figure 4 See Answer T8.
Answer T8
The spatial wavefunction is ψ (x) = A cos(kx) and the probability density is P (x) = | ψ (x) |2 = A2 cos2 (kx). These functions are plotted between x = − π/k to x = +π/k in Figure 4.
The particle is most likely to be found at x = ±π/k and x = 0 where the probability density is a maximum. The particle is least likely to be found at x = ±π/2k where the probability density is zero.
4 A particle confined in one dimension; the one–dimensional box
One of Schrödinger’s primary aims in developing his wave equation was to understand why electrons confined inside atoms could exist only in discrete energy levels. He realized that the wave model of de Broglie could play a key role in that understanding because he knew that mechanical waves, when confined to strings or surfaces or volumes of fixed dimensions, always have certain normal modes, consisting of standing waves, with definite frequencies.
Up to this point we have only been able to argue, by analogy with the situation of confined mechanical waves, that when the de Broglie waves are similarly confined they too should have only certain possible frequencies and wavelengths. Using the de Broglie hypothesis, these definite frequencies or wavelengths translate directly into definite values of energy and momentum and immediately the quantized energies of a confined particle are predicted. Now we can do much better than this because we have a differential equation whose solutions, we suspect, include the required physical wavefunctions and energies.
In this section we see how the case of a particle confined in one–dimensional motion is treated in quantum mechanics. In doing this we will not produce a single result which could not have been correctly predicted from the de Broglie wave approach but we will be introducing a technique which is quite different and which is capable of solving much more difficult problems, such as you will meet later.
4.1 The Schrödinger equation in the one–dimensional box
In one–dimensional confinement the wavefunction of the particle depends on a single position coordinate (e.g. x) and the particle is not allowed outside of a finite range of x–coordinates, say between x = 0 and x = D. The realization of this situation could be a particle held in the space between two parallel infinite planes, separated by a distance D, measured along the x–axis. For example, we might locate one plane at x = 0 and the other at x = D. This is usually called a one–dimensional box – it is actually a box in three–dimensional space, but the confinement is in one dimension only. The particle is completely free to move in y and z but is restricted in x. i We must set the boundary conditions such that the wavefunction is zero everywhere outside the box, since there is no probability of finding the particle there. Also, it is essential that the wavefunction should have only a single value at any given point, since it corresponds to the probability of finding the particle at that point. This requirement, combined with the mathematical demand that ψ (x) should be continuous_functioncontinuous at the boundary, means that the wavefunction must also be zero at the walls (i.e. at x = 0 and x = D).
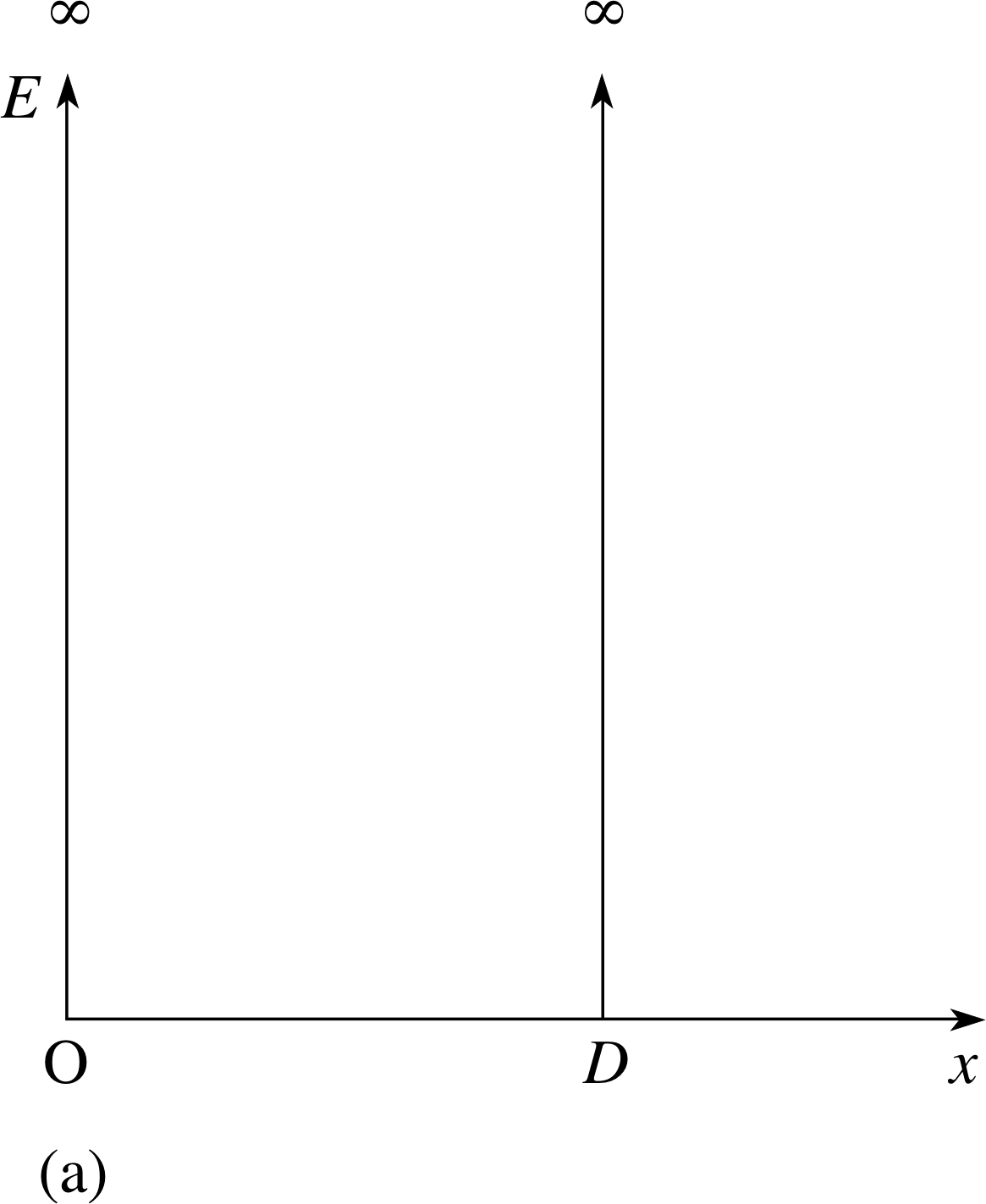
Figure 3a A one–dimensional box, shown as an infinite potential well.
Incidentally, we can indicate that our particle is free to move inside a one–dimensional box, but is incapable of escaping, by noting that its potential energy function, U (x) is:
U (x) = 0 within the interval 0 ≤ x ≤ D
andU (x) = ∞ for x < 0 and x > D
This second condition will prevent the particle escaping from the box, since the particle’s kinetic energy, however large, must be finite.
Figure 3a shows this potential energy function schematically. Any region in which the potential energy is lower than in surrounding regions is known as a potential well; for obvious reasons, this well here is known as an infinite potential well.
In Subsection 3.5 we developed the Schrödinger equation for a free particle (i.e. one for which the potential energy can be set equal to zero everywhere) moving in one-dimension. This situation was represented by the Schrödinger equation:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = E\psi(x)$(Eqn 17)
The general solutions were of the form:
ψ (x) = A exp(ikx) + B exp(−ikx)(Eqn 18)
where A and B are arbitrary (complex) constants, and the energy of the system was related to the constant k by the expression:
$E = \dfrac{\hbar^2k^2}{2m}$(Eqn 19)
In Subsection 3.5 there were no physical restrictions on these solutions and the energy (wholly kinetic) could take any non–negative value.
For the one–dimensional box there are still no forces acting on the particle, except where it encounters a wall. The walls are impenetrable, irrespective of the impact energy of the particle. Therefore we can still set the potential energy to be zero between the walls and can therefore use Equation 17 and its general solution, Equation 18, immediately, provided that we only consider solutions which meet the boundary conditions that ψ = 0 at x = 0 and at x = D, and provided we impose the additional demand that ψ (x) = 0 outside the box. It is more convenient for this problem if we re–write Equation 18 in an equivalent form using sine and cosine functions:
ψ (x) = a cos(kx) + b sin(kx)(20)
where a and b are constants (in general, complex constants).
✦ Rewrite Equation 18 in the form of Equation 20.
✧ Equation 18 is ψ (x) = A exp(ikx) + B exp(−ikx).
Using exp(iθ) = cos θ + i sin θ we can rewrite this as:
ψ (x) = A [cos(kx) + i sin(kx)] + B [cos(−kx) + i sin(−kx)]
Collecting terms:
ψ (x) = (A + B) cos(kx) + i (A − B) sin(kx)
In terms of new constants a = A + B and b = i (A − B) this is:
ψ (x) = a cos(kx) + b sin(kx)
as required.
Substitution of the boundary conditions into Equation 20 gives:
- At x = 0: ψ (0) = 0. This implies that a = 0.
- At x = D: ψ (D) = 0. This implies that b sin(kD) = 0
Assuming b ≠ 0, the second condition gives:
kD = π or 2π or 3π or ... etc.
i.e.$k= \dfrac{\pi}{D},~\dfrac{2\pi}{D},~\dfrac{3\pi}{D},~\dots$
so, there are several possible solutions, each of the form ψn(x) = bn sin(kxx)
where $k_n = \dfrac{n\pi}{D}$ with n = 1, 2, 3, ...(21)
The positive integer n is called a quantum number, in this context. It can be used to label the energy eigenvalues and the corresponding eigenfunctions:
From Equation 19: $E_n = \dfrac{\hbar^2k_n^2}{2m} = \dfrac{n^2\pi^2\hbar^2}{2mD^2} = \dfrac{n^2h^2}{8mD^2}$(22)
inside the box the spatial wavefunctions are: $\psi_n(x) = b_n\sin\left(\dfrac{n\pi x}{D}\right)$(23) i
outside the box the spatial wavefunctions are: ψn(x) = 0
The discrete energy eigenvalues are usually termed energy levels; the first three energy levels and their eigenfunctions are shown in Figure 3b and 3c. These results are identical to those obtained using the primitive idea of de Broglie waves but the approach is quite different. With the de Broglie approach we assume the wavefunction solutions and find the energies. In the Schrödinger approach we assume the Schrödinger equation and deduce both the wavefunction and the energies.
Notice in particular that the energy of the particle is inversely proportional to D2 the square of the size of the confining region. This is a result of fundamental importance for quantum physics.

Figure 3b/c (b) The first three energy levels and (c) the corresponding eigenfunctions in this well.
Atomic energy levels are typically separated by about ten electronvolts (eV) i and this is just the energy scale expected for electrons bound in structures of dimension ≈ 10−10 m. Nuclear energy levels are usually measured in MeV (1 Mev = 106 eV); this is expected for protons or neutrons bound in structures of dimensions ≈ 10−14 m.
You will notice that n = 0 is not on the list of allowed quantum numbers. This is because it would correspond to ψ (x) = 0 inside the box, which we know cannot be true: the particle is in there somewhere. So n = 1 is the lowest allowed quantum number and this means that the minimum value of the kinetic energy of a confined particle is greater than zero. This remarkable conclusion is quite contrary to Newtonian mechanics, where a confined particle can have zero speed and thus zero kinetic energy. The minimum kinetic energy of a confined quantum particle is called the zero point energy and has important physical consequences. For example, even when a material is cooled down to temperatures close to absolute zero, the atomic electrons have non–zero kinetic energies, even in their state of lowest energy, so the electrons can never be regarded as stationary. i
Question T9
Show by direct substitution that ψn(x) = sin(nπx/D) is a solution of the Schrödinger equation (Equation 17),
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = E\psi(x)$(Eqn 17)
with En = n2h2(8mD2). Confirm that ψn(x) = 0 at x = D, provided n is an integer.
Answer T9
If$\psi_n(x) = \sin\left(\dfrac{n\pi x}{D}\right)$
then$\dfrac{d\psi_n(x)}{dx} = n\pi\cos\left(\dfrac{n\pi x}{D}\right)$
and$\dfrac{d^2\psi_n(x)}{dx^2} = n\pi\cos\left(\dfrac{n\pi x}{D}\right)$
Substituting this into the Schrödinger equation:
$\dfrac{-\hbar^2}{2m\os}\left(-\dfrac{n^2\pi^2\hbar^2}{D^2}\right)\psi_n(x) = E\psi_n(x)$
This is satisfied if $E = E_n = \dfrac{n^2\pi^2\hbar^2}{2mD^2} = \dfrac{n^2h^2}{8mD^2}$.
When x = D: $\psi_n(D) = \sin\left(\dfrac{n\pi D}{D}\right) = \sin(n\pi)$, which is zero for any integer n.
Question T10
What is the zero point energy of an electron (mass = 9.1 × 10−31 kg) confined in a one–dimensional box of size 1.0 nm (≈ the diameter of a hydrogen atom)?
Answer T10
For the one–dimensional box, Equation 22,
$E_n = \dfrac{n^2h^2}{8mD^2}$ with n = 1, 2, 3, ...(Eqn 22)
(for n = 1) gives:
$E_1 = \dfrac{h^2}{8mD^2} = \rm \dfrac{(6.63\times10^{-34}\,J\,s)^2}{8\times9.1\times10^{-31}\,kg\times(1.0\times10^{-9}\,m)^2} = 6.03\times10^{-20}\,J = 0.38\,eV$
Question T11
A particle in a one–dimensional box of size D has a wavefunction ψn(x) = sin(2πx/D) with ψn(x) = 0 outside the box. What is the particle’s kinetic energy? Find the x–coordinates where the particle is: (a) least likely and (b) most likely to be found.
Answer T11

Figure 3b/c (b) The first three energy levels and (c) the corresponding eigenfunctions in this well.
If we compare the spatial wavefunction in the box, ψ (x) = sin(2πx D), with the general solution
ψn(x) = bn sin(nπx/D)
we see that the quantum number n must be 2.
The total energy is then given by
$E_2 = \dfrac{2^2h^2}{8mD^2} = \dfrac{h^2}{2mD^2}$
and this is the particle’s kinetic energy since the potential energy is zero inside the box.
The n = 2 spatial wavefunction is shown in Figure 3c.
(a) The particle is least likely to be found at x = 0, D/2 and D, where the probability density function P (x) is zero.
(b) The particle is most likely to be found at x = D/4 and 3D/4, where the probability density function is a maximum.
4.2 Normalization of the wavefunctions
When a particle is trapped in a one–dimensional box the probability of finding the particle somewhere in the box must be 1. We can ensure that each of the spatial wavefunctions ψn(x) in Equation 23,
inside the box the spatial wavefunctions are: $\psi_n(x) = b_n\sin\left(\dfrac{n\pi x}{D}\right)$(Eqn 23)
individually corresponds to a quantum state that meets this requirement by adjusting the arbitrary constant bn in Equation 23 so that the integral of the probability density over the whole box interval, 0 ≤ x ≤ D, is equal to 1. This procedure is called normalization. In mathematical terms normalization implies:

Figure 4 See Answer T8.
$\displaystyle 1 = \int_0^D \lvert\,\psi(x)\,\rvert^2\,dx = b_n^2\int_0^D\sin^2\left(\dfrac{n\pi x}{D}\right)\,dx = \dfrac{b_n^2D}{2}$
Thus $b_n = \sqrt{2/D\os}$, and the normalized wavefunctions are:
$\psi_n(x) = \sqrt{2/D\os}\sin\left(\dfrac{n\pi x}{D}\right)$(24)
For a particle in a stationary state corresponding to any particular one of the spatial wavefunctions, ψn(x), the probability of finding the particle in any interval within the box between positions x = x1 and x = x2 is given by the integral:
$\displaystyle \int_{x_1}^{x_2}P(x)\,dx = \int_{x_1}^{x_2}\lvert\,\psi_n(x)\,\rvert^2\,dx$
This is simply the area under a graph of | ψ (x) |2 (such as Figure 4 in the answer to Question T8) between x = x1 and x = x2.
If however the particle is in a quantum state described by a wavefunction constructed from a combination of energy eigenfunctions, so that
${\it\Psi}\,(x,\,t) = a_1\psi_1(x)\exp(-iE_1t/\hbar) + a_2\psi_2(x)\exp(-iE_2t/\hbar) + \dots + a_N\psi_N(x)\exp(-iE_Nt /\hbar)$
where a1, a2, a3 ... aN, etc. are (complex) constants, then we must impose the additional requirement that
$\displaystyle \int_0^D\lvert\,{\it\Psi}\,(x,t)\,\rvert^2\,dx =1$
Although it is beyond the scope of this module to do so, it may be shown that this leads to the normalization condition:
| a1 |2 + | a2 |2 + | a3 |2 + ... + | aN |2 = 1
where | a1 |2 is the probability that an energy measurement will yield the value E1; and | a2 |2 is the probability of measuring E2; and so on.
5 Including potential energy in the Schrödinger equation
In Newtonian mechanics a knowledge of the potential energy of a particle, subject to conservative forces i,
allows us to use the concept of energy conservation to work out the particle’s motion. Usually, the potential energy varies with position in space and its negative gradient in any direction gives the component of the force on the particle in that direction. For motion in one dimension the potential energy can then be represented by a function of position U (x) and the force on a particle is given by $F_x = -\dfrac{dU(x)}{dx}$.
In quantum mechanics a particle’s potential energy function U (x) i generally plays a role in determining its wavefunction. This quantity must therefore be included in the time–dependent Schrödinger equation that determines Ψ (x, t), and the time–independent Schrödinger equation that determines the spatial wavefunction ψ (x) in a stationary state of given energy. This will enable us to deal with problems involving particles influenced by forces. This potential energy function must accurately represent the potential energy of the system in the region of space in which the solutions of the Schrödinger equation are sought.
5.1 The one–dimensional Schrödinger equation, including potential energy
In Subsection 3.4 we found that the Schrödinger equation for a free particle was the eigenvalue equation for the total energy operator, in this special case where the total energy operator was simply the kinetic energy operator:
$\hat{\rm E}_{\rm kin} = \dfrac{-\hbar^2}{2m\os}\dfrac{d^2}{dx^2}$(Eqn 15)
and the spatial wavefunction corresponding to a stationary state of total energy E = Ekin satisfies
$\hat{\rm E}_{\rm kin}\psi(x) = E_{\rm kin}\psi(x)$(Eqn 16)
In classical physics, when changes in potential energy are also important we write the total energy as the kinetic energy plus the potential energy and, for an isolated i system, it is this total energy which is a constant during the motion. If we try to transfer this energy conservation principle into quantum mechanics it seems eminently sensible to construct a total energy operator by adding a potential energy operator to the kinetic energy operator, as obtained in Subsection 3.4.
The total energy operator, often called the Hamiltonian operator, then becomes:
Hamiltonian operator: $\hat{\rm H} = \hat{\rm E}_{\rm kin} + \hat{\rm E}_{\rm pot} = \left[\dfrac{-\hbar^2}{2m\os}\dfrac{d^2}{dx^2}+U(x)\right]$(25)
and the full time–independent Schrödinger equation in one dimension as:
$\hat{\rm H}\psi(x) = E\psi(x)$, i.e. $\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$(26)
Study comment Equation 26 can in principle be used to solve any fixed energy one–dimensional problem in quantum mechanics, once the appropriate potential energy function U (x) is substituted. However, for the general case of U (x) this solution requires approximation methods. In this module we will look only at a few special cases which can be solved exactly.
Do not be hoodwinked by all this mathematics! We have not derived the time–independent Schrödinger equation; we have simply postulated it, on the basis of consistency with energy conservation and with the operator formalism developed in Section 3. Nevertheless, experience in using this equation reinforces our belief in it – its solutions do appear to be spatial wavefunctions of particles with a definite total energy, moving in one dimension under a potential energy function U (x).
Remember that Equation 26 gives only the spatial parts of the stationary state wavefunctions, i.e. the energy eigenfunctions.
The full wavefunction corresponding to any given quantum state depends on time as well as position, and satisfies the time–dependent Schrödinger equation. We will investigate this equation shortly, but for the moment concentrate on Equation 26 – the time–independent Schrödinger equation. Here is the reason why it is so important:
$\hat{\rm H}\psi(x) = E\psi(x)$, i.e. $\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$(Eqn 26)
Equation 26 is the central result of this module. If we know the potential energy U (x) of a particle moving in one dimension, then we can write down the corresponding time–independent Schrödinger equation (Equation 26). This is an eigenvalue equation for the total energy of the particle. Its solutions are the possible energy eigenvalues of the particle (E1, E2, E3, ...) and the corresponding energy eigenfunctions (ψ1(x), ψ2(x), ψ3(x) ...). The energy eigenfunctions are also the spatial parts of the stationary state wavefunctions
${\it\Psi}_1(x,\,t) = \psi_1(x)\exp(-iE_1t/\hbar),~{\it\Psi}_2(x,\,t) = \psi_2(x)\exp(-iE_2t/\hbar),~{\it\Psi}_3(x,\,t) = \psi_3(x)\exp(-iE_3t/\hbar), \dots$
Each of these stationary state wavefunctions represents a state of definite total energy. Other states, in which the energy does not have a single definite value, may be represented by wavefunctions constructed from combinations of the stationary states, such as
Ψ (x, t) = a1Ψ (x, t) + a2Ψ2(x, t) + ... + aNΨN(x, t)
where a1, a2, a3 ...aN, etc. are complex constants and the normalization of Ψ (x, t) (see Subsection 4.2) requires
| a1 |2 + | a2 |2 + | a3 |2 + ... + | aN |2 = 1
5.2 Solutions in a region where E > U (x)
We will now examine solutions of Equation 26,
$\hat{\rm H}\psi(x) = E\psi(x)$, i.e. $\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$(Eqn 26)
in a region where the total energy E exceeds the potential energy U (x). This qualification corresponds to the kinetic energy being positive, as expected in classical physics.
In the classical world the potential energy can be positive or negative but the kinetic energy must be positive (or zero), so the total energy must always exceed (or equal) the potential energy. In the next subsection we will find that the Schrödinger equation predicts some rather interesting solutions when this condition is violated, but for the moment we will postpone this.
We consider a region where the potential energy is constant at U (x) = U0. In such a region, the Schrödinger equation is:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2psi(x)}{dx^2} = (E-U_0)\psi(x)$(27)
This equation is identical to Equation 16,
$\hat{\rm E}_{\rm kin}\psi(x) = E_{\rm kin}\psi(x)$(Eqn 16)
with the kinetic energy eigenvalue, (E − U0), as the difference between the total energy E and the potential energy U0. The solutions follow immediately from Equations 18 and 19,
$E = \dfrac{\hbar^2k^2}{2m}$(Eqn 19)
Provided E > U0ψ (x) = A exp(ikx) + B exp(−ikx)(Eqn 18)
where A and B are arbitrary constants (complex) and the constant k is related to the kinetic energy (E − U0) by the expression:
$E-U_0 = \dfrac{\hbar^2k^2}{2m}$(28)
The values of k are reduced, relative to their values for the case U0 = 0. Since the momentum of the particle is determined by the value of k this is equivalent to saying that a particle of total energy E travelling through a region with U0 = 0 will have its momentum reduced if it subsequently enters a region where U0 > 0. This is consistent with classical physics – for a given total energy, the kinetic energy must fall if the potential energy rises. Similarly, if U0 < 0 then the kinetic energy is increased.
Question T12
Show by direct substitution that ψ (x) = A exp(ikx) is a solution of the time–independent Schrödinger equation in the case when U (x) has a constant value U0. Confirm that the momentum of the particle is given by $p_x = \hbar k$ and the total energy is given by
$E = \dfrac{p_x^2}{2m} + U_0$
Answer T12
The time–independent Schrödinger equation with U (x) = U0, a constant, is Equation 27,
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2psi(x)}{dx^2} = (E-U_0)\psi(x)$(Eqn 27)
Trying a solution of the form ψ (x) = A exp(ikx) we have, on substitution:
$\dfrac{-\hbar^2}{2m}(-k^2)/psi(x) = (E-U_0)\psi(x)$
This is satisfied if $E = \dfrac{\hbar^2k^2}{2m} + U_0 = \dfrac{p_x^2}{2m} + U_0$
where the momentum eigenvalue is $p_x = \hbar k$.
5.3 Solutions in a region where U (x) > E
In Newtonian mechanics a particle with total energy E cannot enter a region of space where the potential energy function U (x) > E, because to do so would imply a negative kinetic energy. However, there are solutions of Schrödinger’s equation when U (x) > E and physical consequences follow from this.
Again, we consider a region where the potential energy is constant at U (x) = U0 so that the time–independent Schrödinger equation may be written:
$\dfrac{\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = (U_0-E)\psi(x)$(29)
where (U0 − E) is now positive and we have multiplied both sides of Equation 26,
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$(Eqn 26)
by −1 to remove the minus sign on the left–hand side.
The loss of the negative sign is crucial, since the modified differential equation no longer leads to the spatial parts of wave–like wavefunctions. In fact, we can write Equation 29 as:
$\dfrac{d^2\psi(x)}{dx^2} = \dfrac{2m(U_0-E)}{\hbar^2}\psi(x) = \alpha^2\psi(x)$(30)
where$\alpha^2 = \dfrac{2m(U_0-E)}{\hbar^2} \gt 0$(31)
The general solutions of Equation 30 are of the form:
ψ (x) = A exp(αx) + B exp(−αx)(32)
where A and B are arbitrary constants and α can be taken as positive. These solutions are real exponential solutions, not complex exponential solutions.
Question T13
Verify, by direct substitution, that Equation 32 is a solution to Equation 30.
Answer T13
Ifψ (x) = A exp(αx) + B exp(−αx)
then$\dfrac{d\psi(x)}{dx} = \alpha A\exp(\alpha x) - \alpha B\exp(-\alpha x)$
and$\dfrac{d^2\psi(x)}{dx^2} = \alpha^2A\exp(\alpha x) + \alpha^2B\exp(-\alpha x) = \alpha^2\psi(x)$
Question T14
Show that ψ (x) = B exp(−αx) is not an eigenfunction of momentum. Obtain the probability density function P (x).
Answer T14
Operating on the spatial wavefunction ψ (x) = B exp(−αx) with the momentum operator $\hat{\rm p}_x = -i\hbar\dfrac{d}{dx}$ we find:
$-i\hbar\dfrac{d\psi(x)}{dx} = i\hbar\alpha B\exp(-\alpha x) = i\hbar\alpha\psi(x) \ne \text{(real number)}\times\psi(x)$
Since α is real, ψ (x) = B exp(−αx) is not an eigenfunction of momentum. The probability density function
P (x) = | ψ (x) |2 = B2 exp(−2αx), which is a real exponential function which decays as x increases.
The functions A exp(αx) and B exp(−αx) are not travelling waves, nor are they eigenfunctions of momentum. Hence the spatial wavefunction of Equation 32 does not predict a unique momentum. However, the probability density function P (x) is a real quantity and so the theory predicts that:
There is a finite probability that the particle can be found in a region where E < U0, even though this region is forbidden classically.
In the case when B = 0 and α > 0 the spatial wavefunction is a rising exponential as x increases positively, ψ (x) = A exp(αx), and so is the probability density P (x) = | ψ (x) |2 = A2 exp(2αx). If A = 0 and α > 0 both the spatial wavefunction and the probability density are falling exponentials: ψ (x) = B exp(−αx) and | ψ (x) |2 = B2 exp(−2αx), as in the answer to Question T14. In an unbounded region in which x can tend either to +∞ or −∞ only one of these two alternatives will be physically sensible in each of the positive and negative x regions, since the wavefunction cannot be allowed to grow without limit within the range of x.
The possibility of observing a particle in a region of space where the potential energy is greater than the total energy is a purely quantum mechanical effect. The phenomenon is observed in the alpha_decayα–decay of unstable nuclei where the α–particle has to pass through a region of potential energy which is higher than the total particle energy (a so–called potential barrier). Also, in semiconductorsemiconductor devices electrons are found to tunnel through thin films of material in situations where the electric potential would be high enough to exclude the electrons, if the laws of classical physics held. These barrier penetration processes are examples of a process called quantum tunnelling. i
6 The time–dependent Schrödinger equation
Most of this module has been devoted to the time–independent Schrödinger equation and to the energy eigenfunctions (i.e. spatial wavefunctions) that it determines. However, it has also been stressed that the really important quantity in quantum mechanics is the full time–dependent wavefunction, Ψ (x, t), which obeys another differential equation – the time-dependent Schrödinger equation. It is to this equation and the wavefunctions that satisfy it that we now turn our attention.
6.1 Partial derivatives
Wavefunctions such as Ψ (x, t) are functions of two independent variables, x and t. This means that when we consider how Ψ (x, t) changes when x or t changes we can ask questions such as: ‘What is the rate of change of Ψ (x, t) with respect to t while x is held constant?’ or, quite separately: ‘What is the rate of change of Ψ (x, t) with respect to x while t is held constant?’ The answer to both of these questions is found by differentiating Ψ (x, t), but because it is a function of two variables we have to take care to specify what is changing and what is being held constant when the differentiation is performed. This is done by using the mathematical concept of a partial derivative. i For example, the answer to our first question, ‘What is the rate of change of Ψ (x, t) with respect to t while x is held constant?’ is given by the first partial derivative of Ψ (x, t) with respect to t.
This may be denoted in any of the following ways:
$\left.{\dfrac{\partial{\it\Psi}}{\partial t}}\right\rvert_{\text{at constant }x}$ or, more briefly $\left(\dfrac{\partial{\it\Psi}}{\partial t}\right)_x$ or, briefer still $\dfrac{\partial{\it\Psi}}{\partial t}$ i
Similarly, the answer to our second question, ‘What is the rate of change of Ψ (x, t) with respect to x while t is
held constant?’ is given by the partial derivative of Ψ (x, t) with respect to x which may be written $\dfrac{\partial{\it\Psi}}{\partial x}.$
Evaluating partial derivatives is no harder than evaluating ordinary derivatives: you just have to remember to treat x as a constant when differentiating partially with respect to t, and, similarly, to treat t as a constant when differentiating partially with respect to x. A question (which you may prefer to treat as an example) should make the process clear.
✦ If f (x, t) = x2 − xt2, find $\dfrac{\partial f}{\partial x}$ and $\dfrac{\partial f}{\partial t}$.
✧ $\dfrac{\partial f}{\partial x} = 2x - t^2\quad\text{and}\quad\dfrac{\partial f}{\partial t} = -2tx$.
6.2 The time–dependent Schrödinger equation
The fundamental equation of quantum mechanics, the time–dependent Schrödinger equation is a partial differential equation. In a simple one–dimensional case it would take the form:
$-\dfrac{\hbar^2}{2m\os}\dfrac{\partial{\it\Psi}^{\,2}(x,\,t)}{\partial x^2} + U(x,\,t){\it\Psi}\,(x,\,t) = i\hbar\dfrac{\partial{\it\Psi}\,(x,\,t)}{\partial t}$(33) i
where U (x, t) is the potential energy function of the physical system being considered, and Ψ (x, t) is a wavefunction describing that system. In practice, we are usually interested in the wavefunction corresponding to some particular state of the system, and we must determine this from the general solution of Equation 33 by imposing appropriate boundary conditions. If we wanted to consider a different system then the function U (x, t) would have to be changed to represent the new problem.
The time–dependent Schrödinger equation (Equation 33) has many interesting mathematical properties, but we shall note just four of them:
- 1
-
The equation involves i, the square root of –1, this is why complex numbers play an essential role in quantum mechanics.
- 2
-
If the potential energy function is actually independent of time, so that we may replace U (x, t) by U (x) then the time–dependent Schrödinger equation can be shown to have solutions that are separable, that is solutions that may be written in the form:
Ψ (x, t) = ψ (x) ϕ (t) i
where $\phi(t) = \exp(-iEt/\hbar)$ and ψ (x) satisfies the time–independent Schrödinger equation:
$-\dfrac{\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$
These are nothing other than the stationary state wavefunctions we have been concentrating on in this module.
- 3
-
Since the time–independent Schrödinger equation is actually an eigenvalue equation for the total energy, there will generally be several different energy eigenfunctions ψ1(x), ψ2(x), ψ3(x), ψ4(x), ... etc. corresponding to the energy eigenvalues E1, E2, E3, E4, ... etc. Consequently, provided the potential energy is independent of time there will generally be many different stationary state wavefunctions which may be conveniently labelled Ψ1(x, t), Ψ2(x, t), Ψ3(x, t), Ψ4(x, t), ... etc., where
${\it\Psi}_1(x,t\,) = \psi_1(x)\exp(i E_1t/\hbar),~{\it\Psi}_2(x,t\,) = \psi_2(x)\exp(i E_2t/\hbar),~{\it\Psi}_3(x,t\,) = \psi_3(x)\exp(i E_3t/\hbar),~$ ... etc.
- 4
-
The time–dependent Schrödinger equation has the property of linearity, this means that if Ψi(x, t) and Ψj(x, t) are both solutions to the time–dependent Schrödinger equation for a given potential energy function, then Ψ (x, t) = αΨi (x, t) + βΨj (x, t), where α and β are (complex) constants, will also be a solution. This means that once we know the stationary state wavefunctions that correspond to states of definite energy, we can also construct superpositions such as:
${\it\Psi}\,(x,\,t) = \alpha\exp(iE_it/\hbar)\psi_i(x) + \beta\exp(iE_jt/\hbar)\psi_j(x)$
Assuming that Ei ≠ Ej, it is clear that this last wavefunction describes a state in which the system has no definite energy. However, according to quantum mechanics, if the energy of the particle is measured then the result will be either Ei or Ej and the probability of obtaining either result in a sequence of identical measurements is predictable. In fact, if the energy eigenfunctions have been properly normalized, the probability of finding the energy to be Ei will be equal to | α |2 and the probability of finding the energy to be Ej will be equal to | β |2.
7 Closing items
7.1 Module summary
- 1
-
The de Broglie hypothesis connects a particle’s momentum with the angular wavenumber of the associated de Broglie wave, through $p_x = \hbar k$. The kinetic energy is then
$E_{\rm kin} = \dfrac{p_x^2}{2m} = \dfrac{\hbar^2k^2}{2m}$
- 2
-
The total energy is related to the angular frequency of the de Broglie wave by $E = \hbar\omega$.
- 3
-
In quantum mechanics a wavefunction is a complex quantity that provides the most complete possible description of a quantum state. The wavefunction of an unlocalized free particle moving in the x–direction is a complex travelling wave of the form
${\it\Psi}\,(x,\,t) = A\exp\left[i(kx-\omega t)\right] = A\exp\left[i\left(\dfrac{p_x}{\hbar}x-\dfrac{E}{\hbar}t\right)\right]$(Eqn 6)
The Born probability hypothesis is that the probability of finding the particle within the small interval ∆x around the position x at time t is proportional to | Ψ (x, t) |2 ∆x. The function | Ψ (x, t) |2 is known as the probability density.
- 4
-
The wavefunction of a localized free particle, known to be located within a specified region of space, may be represented by a quantum wave packet, composed of a superposition of complex travelling waves with a range of angular wavenumbers, which travels at the wave group velocity.
- 5
-
The wavefunction of a particle with definite total energy E can be written as
${\it\Psi}\,(x,\,t) = \psi(x)\exp\left(-\dfrac{iE}{\hbar}t\right)$(Eqn 10)
where ψ (x) is called the spatial wavefunction. For wavefunctions of this kind the probability density is given by | Ψ (x,t) |2 = | ψ (x) |2 = P (x) and so has no time dependence. These wavefunctions of fixed energy are said to describe stationary states.
- 6
-
In quantum mechanics observables such as energy and momentum correspond to operators. The x–component of momentum of a particle is represented by a differential operator
$\hat{\rm p}_x = -i\hbar\dfrac{d}{dx}$(Eqn 13)
If the spatial wavefunction of a stationary state is an eigenfunction of momentum then the momentum eigenvalue px can be found by solving the eigenvalueeigenvalue equation
$\hat{\rm p}_x\psi(x) = p_x\psi(x)$(Eqn 14)
For example, if $\psi(x) = A\exp\left(\dfrac{ip_xx}{\hbar}\right)$ then the momentum eigenvalue is px and this is also the definite outcome of a momentum measurement.
- 7
-
The kinetic energy of a particle is represented by the differential operator
$\hat{\rm E}_{\rm kin} = \dfrac{\hbar^2}{2m\os}\dfrac{d^2}{dx^2}$
If the wavefunction of the particle is a stationary state wavefunction then its spatial part is an eigenfunction of kinetic energy. The kinetic energy eigenvalue Ekin can then be found by solving the eigenvalue equation
$\hat{\rm E}_{\rm kin}\psi(x) = E_{\rm kin}\psi(x)$
and this value would be the definite outcome of a kinetic energy measurement. On the other hand, if the wavefunction is a combination of stationary state wavefunctions then the outcome of an energy measurement might be any one of the corresponding energy eigenvalues, and the wavefunction can be used to predict the probability of each such value.
- 8
-
The time–independent Schrödinger equation for any system is simply the eigenvalue equation for the total energy of the system. For a free particle moving in one dimension and where the potential energy is zero this equation is
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = E\psi(x)$(17)
The spatial wavefunctions for the free particle are solutions of this equation.
- 9
-
The time–independent Schrödinger equation predicts that the energy of a particle confined in a one–dimensional box, length D, can take only certain values, these energy levels are given by the expression:
$E_n = \dfrac{\hbar^2k^2}{8mD^2}$ with n = 1, 2, 3, ...(Eqn 22)
The corresponding spatial wavefunctions inside the box are given by:
$\psi_n(x) = b_n\sin\left(\dfrac{n\pi x}{D}\right)$(Eqn 23)
Outside the box ψn(x) = 0. The particle has a minimum possible energy called the zero point energy when the quantum number n = 1. The zero point energy is inversely proportional to D2.
- 10
-
With normalized wavefunctions the probability of finding the particle in a small interval ∆x close to x is P (x) ∆x = | ψ (x) |2 ∆x.
The spatial wavefunctions of a particle in a one–dimensional box can be normalized by setting the arbitrary constant $b_n = \sqrt{2/D\os}$; they then satisfy the condition
$\displaystyle \int_0^D\lvert\,{\rm\Psi}(x,\,t)\,\rvert^2\,dx = 1$
- 11
-
With the inclusion of a potential energy function U (x), the operator for the total energy is called the Hamiltonian operator:
$\hat{\rm H} = \hat{\rm E}_{\rm kin} + \hat{\rm E}_{\rm pot} = \left[\dfrac{-\hbar^2}{2m\os}\dfrac{d^2}{dx^2}+U(x)\right]$(Eqn 25)
and the time-independent Schrödinger equation for a particle moving in one dimension is:
$\hat{\rm H}\psi(x) = E\psi(x)$, i.e. $\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x)$(Eqn 26)
Spatial wavefunctions, and hence stationary state wavefunctions, for a wide variety of one–dimensional problems can be found by solving this equation, with an appropriate potential energy function inserted and with appropriate boundary conditions imposed on the solutions.
- 12
-
The solutions of the time–independent Schrödinger equation for a particle moving in a uniform constant potential U0, with E > U0, are
ψ (x) = A exp(ikx) + B exp(−ikx)(Eqn 18)
with kinetic energy $E-U_0 = \dfrac{\hbar^2k^2}{2m}$
This energy eigenfunction is a combination of two functions, each of which is also a momentum eigenfunction.
- 13
-
The solutions of the time–independent Schrödinger equation for a particle moving in a uniform constant potential U0, with E < U0, are linear combinations of real exponential functions:
ψ (x) = A exp(αx) + B exp(−αx)
with $\alpha^2 = \dfrac{2m(U_0-E)}{\hbar^2}$ and with the positive root taken for α.
The Schrödinger equation here predicts that a particle can penetrate some distance into a region forbidden by classical physics, where the potential energy exceeds the total energy. These solutions provide an explanation of quantum tunnelling.
- 14
-
The time-dependent Schrödinger equation, for a system consisting of a single particle of mass m moving in one dimension with potential energy U (x, t), is the partial differential equation
$-\dfrac{\hbar^2}{2m\os}\dfrac{\partial{\it\Psi}^{\,2}(x,\,t)}{\partial x^2} + U(x,\,t){\it\Psi}\,(x,\,t) = i\hbar\dfrac{\partial{\it\Psi}\,(x,\,t)}{\partial t}$(Eqn 33)
This is the central equation of quantum mechanics. Its solutions Ψ (x, t), subject to appropriate boundary conditions, are the wavefunctions and describe the possible quantum statestates of the system. A wavefunction is generally a complex quantity and is not directly measurable, but it may be used to obtain (probabilistic) information about the behaviour of the system.
7.2 Achievements
After completing this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Write expressions for the de Broglie wave and the quantum mechanical wavefunction of an unlocalized free particle moving in one dimension with momentum px and total energy E.
- A3
-
Define the differential operators for the momentum and for the kinetic energy of a particle moving in one-dimension.
- A4
-
Describe a test to determine whether or not a given function is an eigenfunction of a given operator.
- A5
-
Describe the relationship between an eigenvalue equation and the measurement of the corresponding observable.
- A6
-
Recall the time–independent Schrödinger equation for a free particle moving in one-dimension.
- A7
-
Recall the Born probability interpretation of the wavefunction and relate this to the idea of a stationary state.
- A8
-
Use the time–independent Schrödinger equation to predict the energy levels and corresponding eigenfunctions of a particle confined in a one–dimensional box. Demonstrate the role of boundary conditions on the eigenfunctions in deriving these results.
- A9
-
Recall how the energy levels of a particle in a one–dimensional box depend on the quantum number n and the size of the box. Recall the shape of the eigenfunctions for the first few energy levels.
- A10
-
Explain how the eigenfunctions for a particle, confined in a one–dimensional box, can be normalized so that the probability of observing the particle in a given region can be calculated.
- A11
-
Interpret the energy levels in real physical systems in terms of the results of the idealized one–dimensional box.
- A12
-
Write down the time–independent Schrödinger equation for a particle moving in one dimension, with a potential energy described by a potential energy function U (x).
- A13
-
Describe the general behaviour of the solutions of the Schrödinger equation for one–dimensional motion, where the potential energy is constant.
- A14
-
Explain how particles can penetrate into regions where the total energy is less than the potential energy, and use the solutions of the Schrödinger equation for one–dimensional motion to explain the phenomenon of quantum tunnelling.
- A15
-
Write down the time–dependent Schrödinger equation and explain the significance of the property of linearity that it possesses.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
7.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A3, A4 and A5)
The spatial wavefunction of a particle moving parallel to the x–axis is
ψ (x) = A cos(qx) + B sin(qx)
where q is a positive real number.
Show that ψ (x) is an eigenfunction of momentum if B = iA.
What would then be the result of a measurement of momentum on a particle in a stationary state with this spatial wavefunction?
Show that this ψ (x) is also an eigenfunction of kinetic energy for any values of A and B. What would be the result of a measurement of kinetic energy?
Answer E1
The operator for momentum is
$\hat{\rm p}_x = -i\hbar\dfrac{d}{dx}$
Applying this to the spatial wavefunction ψ (x) = A cos(qx) + B sin(qx) gives:
$-i\hbar\dfrac{d\psi(x)}{dx} = -i\hbar[-qA\sin(qx) + qB\cos(qx)]$
If B = iA we also have A = −iB. Substituting these we find:
$-i\hbar\dfrac{d\psi(x)}{dx} = -i\hbar[qiA\sin(qx) + qiA\cos(qx)] = \hbar q[A\cos(qx) + B\sin(qx)] = \hbar q\psi(x)$
The spatial wavefunction is therefore an eigenfunction of momentum with eigenvalue $\hbar q$. A measurement of
momentum on a particle in this state would give the result $\hbar q$.
The operator for kinetic energy is $\hat{\rm E}_{\rm kin} = \dfrac{-\hbar^2}{2m\os}\dfrac{d^2}{dx^2}$. Applying this to the spatial wavefunction gives:
$\dfrac{-\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = \dfrac{-\hbar^2}{2m\os}(-q^2)[A\cos(qx) + B\sin(qx)] = \dfrac{\hbar^2q^2}{2m\os}\psi(x)$
This spatial wavefunction is an eigenfunction of kinetic energy, for any values of A and B. The eigenvalue and the result of a measurement of kinetic energy is $\dfrac{\hbar^2q^2}{2m}$.
(Reread Subsections 3.1 to 3.3 if you had difficulty with this question.)
Question E2 (A5, A6 and A7)
An electron (mass = 9.1 × 10−31 kg) is in a stationary state described by the spatial wavefunction ψ (x) = A cos(kx) with k = 1.5 × 1010 m−1.
(a) Show that the wavefunction is a solution of the free particle Schrödinger equation. What is the electron energy in eV?
(b) What are the possible results of a measurement of momentum?
Answer E2
(a) The spatial wavefunction is ψ (x) = A cos(kx) and the first and second derivatives are
$\dfrac{d\psi(x)}{dx} = -kA\sin(kx)$
and$\dfrac{d^2\psi(x)}{dx^2} = -k^2A\cos(kx) = -k^2\psi(x)$
Substitute into the free particle time–independent Schrödinger equation
$\dfrac{\hbar^2k^2}{2m}\psi(x) = E\psi(x)$
This is satisfied and so ψ (x) = A cos(kx) is a solution if $E = \dfrac{\hbar^2k^2}{2m}$
We are given that k = 1.5 × 1010 m−1 and m = 9.1 × 10−31 kg so that:
$E = \rm \dfrac{(1.05\times10^{-34}\,J\,s\times1.5\times10^{10}\,m^{-1})^2}{(2\times9.1\times10^{-31}\,kg)} = 1.36\times10^{-18}\,J = 8.5\,eV$
(b) ψ (x) = A cos(kx) may be written, using Euler’s relation, as the sum of two momentum eigenfunctions
$\psi(x) = \dfrac A2\left[\exp(ikx) + \exp(-ikx)\right]$
The result of a measurement of momentum is either $p_x = \hbar k$ or $p_x = -\hbar k$, with equal probability.
(Reread Subsections 3.2 to 3.5 if you had difficulty with this question.)
Question E3 (A8)
Describe in words how the time–independent Schrödinger equation is solved for a particle in a one–dimensional box. Why are certain boundary conditions imposed and how does this lead to quantized energy levels?
Answer E3
The spatial wavefunction must be a solution of the free particle Schrödinger equation inside the box. The particle cannot escape from the box so ψ (x) = 0 outside. Inside the box ψ (x) → 0 at the edges because the wavefunction cannot have two values at any point and must be continuous.
Suitable solutions of the time–independent Schrödinger equation are ψ (x) = A sin(kx) or B cos(kx). If ψ (x) is to be zero at the boundaries (x = 0 and x = D) then we must use ψ (x) = A sin(kx), and set k = nπ/D.
The time–independent Schrödinger equation then gives the corresponding particle energy as $E = \hbar^2k^2/(2m)$ and substituting for k gives the solutions:
$E = \dfrac{n^2h^2}{2mD^2} = \dfrac{n^2h^2}{8mD^2}$
(Reread Subsection 4.1 if you had difficulty with this question.)
Question E4 (A9 and A10)
The normalized spatial wavefunction for a particle in a one–dimensional box is:
$\psi(x) = \sqrt{2/D\os}\sin\left(\dfrac{\pi x}{D}\right)$ 0 ≤ x ≤ D and otherwise ψ (x) = 0
(a) What is the result of a measurement of the energy?
(b) Confirm that the probability of finding the particle somewhere within the box is 1.
(c) Show that the probability of finding the particle between x = 0 and x = D/2 is exactly 0.5.
[Hint: You do not need to do the integral, just consider the shape of | ψ (x) |2.]
Answer E4

Figure 3b/c (b) The first three energy levels and (c) the corresponding eigenfunctions in this well.
(a) Compare this wavefunction with the solutions for a particle in a one–dimensional box, Equation 22 and 23 and Figure 3:
$E_n = \dfrac{\hbar^2k_n^2}{2m} = \dfrac{n^2\pi^2\hbar^2}{2mD^2} = \dfrac{n^2h^2}{8mD^2}$(Eqn 22)
inside the box the spatial wavefunctions are:
$\psi_n(x) = b_n\sin\left(\dfrac{n\pi x}{D}\right)$(Eqn 23)
The quantum number n = 1 and so the particle must have energy
$E_1 = \dfrac{\hbar^2\pi^2}{2mD^2}\text{, i.e. }\dfrac{h^2}{8mD^2}$
(b) The probability of finding the particle in the small interval dx is equal to P (x) ∆x = | ψ (x) |2 ∆x if the spatial wavefunction is normalized. The total probability of finding the particle somewhere in the box is then given by summing P (x) ∆x from x = 0 to x = D (since ψ (x) = 0 outside the box). In the limit as ∆x → 0 this becomes:
total probability = $\displaystyle \int_0^DP(x)\,dx$
so, using an appropriate trigonometric identity
$\displaystyle \int_0^DP(x)\,dx = \dfrac2D\int_0^D\sin^2\left(\dfrac{\pi x}{D}\right)\,dx = \dfrac1D\int_0^D\left[1-\cos\left(\dfrac{\pi x}{D}\right)\right]\,dx = \dfrac1D\left[x-\left(\dfrac{D}{2\pi}\right)\sin\left(\dfrac{\pi x}{D}\right)\right]_0^D = 1$
as expected.
(c) From the spatial wavefunction for n = 1 in Figure 3 it can be seen that the curve is symmetric about x = D/2. The probability function, which depends on the square of ψ (x), is therefore also symmetric about x = D/2 so that the area under the P (x) curve from x = 0 to x = D/2 must be just half the total area. The probability of observing the particle with x < D/2 is just 0.5.
(Reread Section 4 if you had difficulty with this question.)
Question E5 (A9 and A11)
A very crude (one-dimensional) model of an atomic nucleus assumes that protons are confined to a region 10−14 m in size. Estimate the difference in energy, in MeV units, between the first two energy levels. (Mass of a proton mp = 1.67 × 10−27 kg.)
Answer E5
The energy levels in a one–dimensional box, size D, are given by Equation 22: En = n2h2/(8mD2). Put in the mass of the proton mp = 1.67 × 10−27 kg and D = 10−14 m and we find:
$E_n = \dfrac{n^2(6.63\times10^{-34}\,{\rm J\,s})}{(8\times1.67\times10^{-27}\,{\rm kg}\times10^{-28}\,{\rm m^2})} = 3.29\times10^{-13}n^2\,{\rm J} = 2.06n^2\,{\rm MeV}$
The difference between the n = 2 and n = 1 energy levels is given by: E2 − E1 = (4 − 1) × 2.06 MeV = 6.18 MeV. This energy difference, on the MeV scale, is typical of what is found experimentally in nuclear physics.
(Reread Section 4 if you had difficulty with this question.)
Question E6 (A11, A12, A13 and A14)
(a) What is the general solution of the time–independent Schrödinger equation for a particle moving in one-dimension, where the potential energy is a constant, U0, which is greater than the total energy E?
(b) An electron (mass me = 9.1 × 10−31 kg) of total energy 5 eV is in the region of space of positive x and the potential energy is 10 eV. The spatial wavefunction is ψ (x) = B exp(−αx) with α > 0. Find the value of α (the units are m−1). Over what distance from x = 0 does the probability density of observing the electron decrease by a factor of 10?
Answer E6
The solution of the time–independent Schrödinger equation,
$\dfrac{\hbar^2}{2m\os}\dfrac{d^2\psi(x)}{dx^2} = (U_0-E)\psi(x)$(Eqn 29)
in a region where E < U0 is of the form:
ψ (x) = A exp(αx) + B exp(−αx)
The positive real constant α is given by Equation 31 as:
$\alpha = \dfrac{\sqrt{\smash[b]{2m(U_0-E)\os}}}{\hbar}$
(b) In a region of positive x and with positive α we must exclude the positive exponential term in order for the wavefunction to remain finite. α is real, providing U0 > E. Substituting the data, E = 5 eV, U0 = 10 eV gives:
$\alpha = \dfrac{\sqrt{\smash[b]{2m(U_0-E)\os}}}{\hbar} = \rm \dfrac{\sqrt{\smash[b]{2\times9.1\times10^{-31}\,kg\times5\times1.6\times10^{-19}\,J}}}{1.05\times10^{-34}\,J\,s} = 1.1\times10^{10}\,m^{-1}$
P (x) = | ψ (x) |2 = B2 exp(−2αx) so, that for a factor of 10 reduction:
$0.1 = \dfrac{\lvert\,\psi(x)\,\rvert^2}{\lvert\,\psi(0)\,\rvert^2} = \dfrac{B^2\exp(-2\alpha x)}{B^2\exp(0)} = \exp(-2\alpha x)$
sox = loge (0.1)/(−2α) = 1.0 × 10−10 m
(Reread Subsection 5.3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 7Closing items.