PHYS 10.2: A wave model for matter |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Imagine a world in which knowing exactly how fast an object is travelling means that you have no idea where it is, or where the act of passing through an open doorway can alter your direction of travel in an unpredictable way. You might think that such a world would be pure science fantasy – but, prepare to be surprised; this is the world we live in, according to quantum physics. The reason that this description of the world seems to run contrary to common sense is that these phenomena are normally only significant for microscopic entities with sizes comparable to atoms or nuclei. For everyday–sized macroscopic objects, the effects are usually too small to be observed. Nevertheless, quantum physics has enormous relevance to everyday life, mainly because it has allowed us to develop a detailed understanding of the internal structure of atoms and the behaviour of subatomic particles. This has not only led to great advances in chemistry but also to the development of the semiconductor industry – the basis of modern electronics and computing technology. Furthermore, the consequences of quantum theory spill over into the realm of philosophy and pose profound questions about the nature of the Universe.
In this module, we will be concerned primarily with an understanding of the fundamental principles of quantum physics rather than its application to atomic structure, which is dealt with elsewhere in FLAP. However, by the end of the module, you will be aware of the importance of the theory and also why the statements with which we began this introduction are indeed true for our world.
We begin in Section 2 with the historical background to quantum theory and the concept of de Broglie waves. Section 3 deals with the physical interpretation of the de Broglie hypothesis which leads on to the idea of the Heisenberg uncertainty principle in Section 4. Some applications of quantum physics are described in Section 5, including the determination of crystal structure, the tunnel effect and the measurement of atomic sizes; Section 6 briefly examines some of the philosophical issues raised by quantum theory.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 7.1Module summary and the Subsection 7.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 7.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Data for the Fast track questions:
- speed of light in a vacuum, c = 3.00 × 108 m s−1
- mass of the electron, me = 9.11 × 10−31 kg
- Planck’s constant h = 6.63 × 10−34 J s
Question F1
(a) Estimate the de Broglie wavelengths of:
(i) a housefly in flight,
(ii) a neutron of mass 1.7 × 10−27 kg travelling at 1% of the speed of light in a vacuum.
(b) At what speed should a beam of electrons be travelling to produce similar diffraction effects to a beam of X–rays with a frequency of 2.0 × 1018 Hz?
Answer F1
(a) The de Broglie relationship is λdB = h/p and p = mυ.
(i) Taking the mass of a fly to be 10−3 kg and its speed to be 2 m s−1 we find
$\lambda_{\rm dB} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{10^{-3}\,kg\times2\,m\,s^{-1}} \approx 3.3\times10^{-31}\,m$
(ii) Taking the speed of light as 3.00 × 108 m s−1, for the neutron υ = c/100
$\lambda_{\rm dB} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{1.7\times10^{-27}\,kg\times3.00\times10^6\,m\,s^{-1}} \approx 1.3\times10^{-13}\,m$
(b) To produce the same diffraction effects, the electrons should have the same de Broglie wavelength as the X–rays.
For X–rays, λ = c/f and for the electrons $\lambda_{\rm dB} = \dfrac hp = \dfrac{h}{m_{\rm e}\upsilon}$
So$\dfrac{h}{m_{\rm e}\upsilon} = \dfrac cf$
i.e.$\upsilon = \dfrac{hf}{m_{\rm e}c} = \rm \dfrac{6.63\times10^{-34}\,J\,s\times2.0\times10^{18}\,s^{-1}}{9.11\times10^{-31}\,kg\times3.00\times10^8\,m\,s^{-1}} = 4.85\times10^6\,m\,s^{-1}$
Question F2
A friend with an interest in science but with no knowledge of quantum physics tries to convince you that it should be possible to direct a beam of electrons to a particular location with arbitrary precision, simply by passing them through an aperture which is sufficiently small. In about 200 words, give an argument to show that this reasoning is incorrect.
Answer F2
Your explanation might run along the following lines:
The motion of all particles is governed by their associated de Broglie waves which propagate in the same way as physical waves such as water waves or sound waves. This implies that they are diffracted when they pass through an aperture and interfere when they are superposed. Diffraction means that a wave motion which was travelling in a particular direction before reaching the aperture spreads out over a range of angles as it passes through. The significance of the de Broglie wave for a particle is that the intensity (or the square of the amplitude) of the wave at a point represents the probability of finding the particle at that point. Thus, the effect of passing a beam of electrons through an aperture is to cause the beam to spread out and the smaller the aperture, the greater will be the diffraction effect and hence the greater the spread of the beam. Passing a beam of electrons through a very small hole is therefore not a good way of ensuring they arrive at a particular location.
One could also argue from the Heisenberg uncertainty principle that passing the electrons through a hole is effectively making a measurement of their position. The smaller the hole, the less the uncertainty in position and therefore the greater the uncertainty in momentum perpendicular to the direction of travel. Again, this is demonstrated by the spreading of the beam.
Question F3
(a) Calculate the minimum fractional uncertainty with which it is possible to measure the magnitude of the momentum of an electron travelling at a nominal speed of 2.0 × 105 m s−1, if a simultaneous measurement gives its position to within ±1 × 10−10 m.
(b) Describe the way in which the time taken to make a measurement of the energy of a particle influences the uncertainty of the measured energy.
Answer F3
(a) From the Heisenberg uncertainty principle $\Delta x\,\Delta p_x \gtrsim \hbar$ where ∆x is 2 × 10−10 m. The minimum uncertainty in momentum is then
$\Delta p_x \approx \dfrac{\hbar}{\Delta x} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{2\pi\times2\times10^{-10}\,m} \approx 5\times10^{-25}\,kg\,m\,s^{-1}$
The nominal momentum of the electron is
px = meυx = 9.11 × 10−31 kg × 2.0 × 105 m s−1 = 1.8 × 10−25 kg m s−1
So the fractional uncertainty is:
$\dfrac{\Delta p_x}{p} \approx \rm \dfrac{5\times10^{-25}\,kg\,m\,s^{-1}}{1.8\times10^{-25}\,kg\,m\,s^{-1}} = 2.8$, i.e. 280%
So px could at best be known to within ±140% of its nominal value.
(b) According to one interpretation of the Heisenberg uncertainty principle, Equation 16b,
Heisenberg uncertainty principle $\Delta E\,\Delta t \gtrsim \hbar$(Eqn 16b)
if a particle is observed over a time ∆t, then its energy can only be known in principle to within an uncertainty $\Delta E \gtrsim \hbar/\Delta t$.
For macroscopic measurements, this ‘in principle’ limit is too small to be of any consequence. For measurements at an atomic scale (for example in the determination of energy levels in an atom) it may be important.
1.3 Ready to study?
Study comment In order to study this module, you will need to be familiar with the following terms: acceleration, components_of_a_vectorcomponent (of a vector), electric charge, electric potential, electric potential energy, electromagnetic radiation, force, kinetic energy, magnitude_of_a_vector_or_vector_quantitymagnitude (of a vector), momentum, Newton’s laws of motion, potential energy, scalar, vector and wavewave motion (including amplitude, angular wavenumber (k = 2π/λ), diffraction, frequency, interference, intensity, wavelength). You should also understand what is meant by the principle of superposition with regard to wave motion and appreciate how waves are diffracted at a single slit and at multiple slits, although these topics are briefly reviewed in Subsection 2.3. In addition, you should be able to carry out simple calculations which include algebraic manipulations and trigonometry. Subsection 5.3 uses simple differentiation, but the details of this are not essential to meet the achievements of this module. If you are uncertain about any of these terms, you can review them now by referring to the Glossary which will indicate where in FLAP they are discussed. The following Ready to study questions will allow you to establish whether or not you need to review some of these topics before embarking on this module.
Data for the Ready to study? questions:
- magnitude of the acceleration due to gravity g = 9.81 m s−2
- speed of light in a vacuum, c = 3.00 × 108 m s−1
Question R1
A car of mass 1500 kg is travelling at a speed of 35.0 m s−1. Calculate the magnitude of its momentum and its kinetic energy.
Answer R1
The magnitude of the momentum p is the product of mass m and speed υ.
p = mυ = 1500 kg × 35.0 m s−1 = 5.25 × 104 kg m s−1
Kinetic energy Ekin = ½mυ2 = ½ × 1500 kg × (35.0 m s−1)2 = 9.19 × 105 J
Consult momentum and kinetic energy in the Glossary for further information.
Question R2
(a) A beam of light travelling through a vacuum has a wavelength of 4.50 × 10−7 m. Calculate its frequency.
(b) The same beam of light then passes through a tank of water in which its speed is reduced by a factor of 1.33. Calculate the wavelength λ and the angular wavenumber 2π/λ of the light beam in the water.
Answer R2
(a) f = υ/λ where f is frequency, υ is wave speed and λ is wavelength, so:
$f = \rm \dfrac{3.00\times10^8\,m\,s^{-1}}{4.50\times10^{-7}\,m} = 6.67\times10^{14}\,Hz$
(b) In the water, the frequency remains the same so the new wavelength λw is given by:
$\lambda_{\rm w} = \rm \dfrac{3.00\times10^8\,m\,s^{-1}}{1.33\times6.67\times10^{14}\,s^{-1}} = 3.38\times10^{-7}\,m$
The angular wavenumber is:
$k = \dfrac{2\pi}{\lambda} = \rm \dfrac{2\pi}{3.38\times10^{-7}\,m} =1.86\times10^7\,m^{-1}$
Consult frequencyfrequency of light and angular wavenumber in the Glossary for further information.
Question R3
Two wave generators in a ripple tank produce two sets of ripples with the same frequency. At a particular point on the surface of the tank, one generator operating alone produces ripples of amplitude 1.5 cm while the other produces ripples of amplitude of 2.0 cm. What are the maximum and minimum possible amplitudes for the composite ripples when both generators are switched on together?
Answer R3
According to the principle of superposition, the maximum amplitude of the composite wave will be the sum of the individual amplitudes (3.5 cm) and the minimum amplitude will be equal to the difference between the individual amplitudes (0.5 cm). The exact amplitude of the composite wave will depend on the relative phase of the two wave generators.
Consult the Glossary for further information.
Question R4
Estimate the potential difference through which an initially stationary electron must be accelerated to give it a speed of 4.0 × 105 m s−1. (Take the electron’s mass and charge to be, respectively, 9.1 × 10−31 kg and 1.6 × 10−19 C.)
Answer R4
For a stationary charge q accelerated by a potential difference V the final kinetic energy Ekin is given by
Ekin = qV
SoEkin = ½ mυ2 = qV
and$V= \dfrac{m_{\rm e}\upsilon^2}{2q} = \rm \dfrac{9.1\times10^{-31}\,kg\times(4.0\times10^5\,m\,s^{-1})^2}{2\times1.6\times10^{-19}\,C} = 0.46\,V$
Consult the Glossary for further information.
Question R5
A plane wave passes through a pair of slits in a barrier which is perpendicular to the initial direction of propagation of the wave. Show that, after passing through the slits, the wave amplitude varies with angle θ relative to the initial direction such that amplitude maxima occur for values of θ given by nλ = d sin θ where d is the separation between the slits and n is an integer.
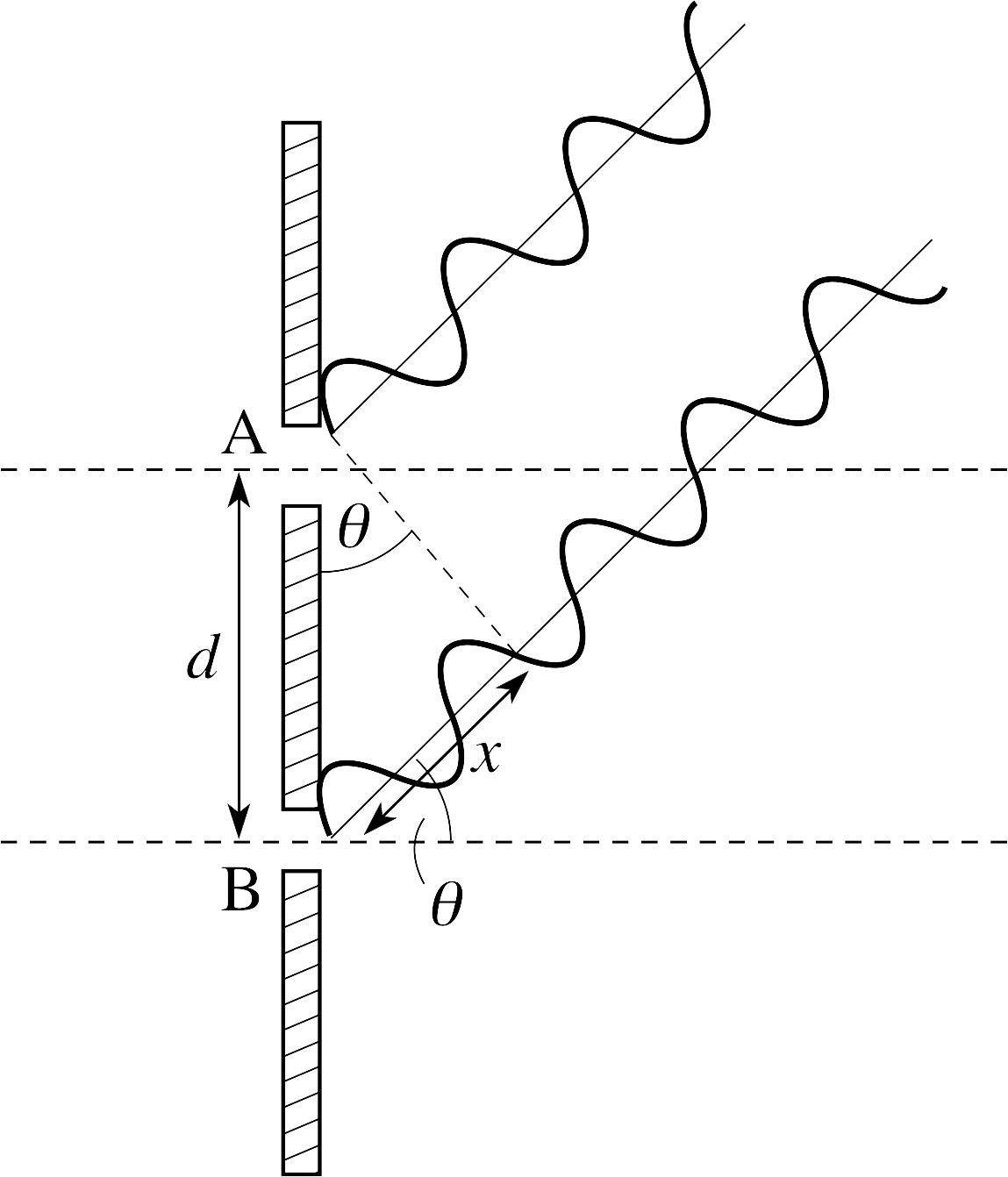
Figure 11 See Answer R5.
Answer R5
Figure 11 shows waves leaving both slits in the direction θ. It can be seen that the wave from slit B must travel an extra distance x where x = d sin θ.
For maximum amplitude, the path difference must represent a whole number of wavelengths, so nλ = x = d sin θ.
(Figure 11 actually shows a destructive minimum.)
2 The de Broglie hypothesis and its verification
2.1 Thirty years that changed our perception of the world
It is important to see the development of quantum theory in its historical context. At the end of the 19th century, many scientists thought that all the interesting problems of physics had been solved. Newtonian mechanics had explained the motion of objects throughout the Universe, while all electromagnetic phenomena, including visible light, could be understood in terms of the theories of James Clerk Maxwell (1831–1879). Even the behaviour of large populations of molecules in gases could be successfully modelled using statistical theories and the relationship between heat and other forms of energy was elegantly described by the laws of thermodynamics. Furthermore, throughout the 19th century this theoretical understanding had stimulated technological developments which revolutionized life in western Europe. i
There just seemed to be a few loose ends to tidy up before physics could be said to have completed its task. These ‘loose ends’ included the internal structure of atoms, some unexplained observations concerning the so–called photoelectric effect and the fact that the speed of light appeared to be constant irrespective of the relative motion of the observer and light source. The fundamentals of the answers to these problems were worked out in the first 30 years of this century but, rather than the tidying up of a few loose ends, they involved a radical rethink of the whole of physics and of the way we understand the Universe.
In fact, the beginning of the 20th century is seen as such a watershed that physics as it was understood up to that point is called classical physics and most of the developments since then, fall in a new category, termed quantum physics. Quantum physics is now seen as one of the most important theories ever to emerge from within physics, embracing as it does all the elements of classical physics as well as the new discoveries.
2.2 The de Broglie hypothesis
We will pick up the story in 1905. This was an amazing year for Albert Einstein (1879–1955). As well as his work on relativity, he published two other papers of great importance. One of these was an attempt to explain some features of the so–called photoelectric effect – the emission of electrons from a metal surface when illuminated by electromagnetic radiation. We need not go into the details of these observations here, as they are covered elsewhere in FLAP. i It is sufficient to say that Einstein showed that the puzzling features could be neatly explained by assuming that when electromagnetic radiation interacts with matter, the energy transfer occurs only in discrete amounts, with magnitude proportional to the radiation frequency. These quanta of electromagnetic energy later became known as photons and the quantum of energy, E, associated with radiation of frequency f is:
photon energy E = hf(1)
where h, the constant of proportionality, has a value of 6.63 × 10−34 J s. A similar idea had already been postulated by Max Planck (1858–1947) to explain the spectrum of radiation emitted by heated objects (so-called black–body radiation). Thus Equation 1 is often referred to as the Planck–Einstein formula and the constant h is known as Planck’s constant.
Planck and Einstein were suggesting that electromagnetic energy has a granular or ‘lumpy’ nature. These ideas were greeted with a degree of scepticism as they did not fit well with the previous understanding of electromagnetic radiation as a wave phenomenon. Indeed Planck himself felt that, although the mathematics was correct, the physical interpretation of radiant energy as ‘lumpy’ was probably flawed.
However, in 1923, the physicist Arthur H. Compton (1892–1962) took things a stage further by showing that when electromagnetic radiation, in the form of X–rays, was made to collide with electrons in a metal, its behaviour was exactly consistent with that of an interaction involving particles with energy E, as in Equation 1 and momentum magnitude i p given by:
photon momentum $p = \dfrac{hf}{c} = \dfrac Ec$(2)
where c is the speed of light. This scattering phenomenon later became known as the Compton effect and gave credence to the existence of the photon as an independent particle.
Question T1
Show that the momentum magnitude of a photon can also be expressed by the following equation:
photon momentum $p = \dfrac{h}{\lambda}$(3)
Answer T1
For an electromagnetic wave in vacuum λ = c/f where c is the speed of light in a vacuum.
Substituting for c in Equation 2,
photon momentum $p = \dfrac{hf}{c} = \dfrac Ec$(Eqn 2)
gives Equation 3,
photon momentum $p = \dfrac{\lambda}{h}$(Eqn 3)
Prince Louis de Broglie (1892–1987) i was at that time a research student in Paris who became fascinated by these exciting new ideas. As part of his PhD thesis, he tried to resolve the apparent conflict between the discrete nature of light energy, and the strong evidence of wave behaviour provided by the phenomena of diffraction and interference. He suggested that the disparity between wave and particle viewpoints might not be as great as it seemed. In particular, he proposed that a relation similar to Equation 3, linking a particle–like property (p) to a wave–like property (λ) might be a general feature of quantum physics. In this way ‘particles’such as electrons, atoms, dust grains – perhaps even billiard balls – might be associated with waves. De Broglie was not clear about the nature of these waves though he certainly felt that in some way the presence of the waves influenced the presence of the particle.
The essential point of de Broglie’s proposal can now be stated as follows:
the de Broglie hypothesis:
Any particle with momentum magnitude p may be associated with a wave whose de Broglie wavelength λdB is given by:
$\lambda_{\rm dB} = \dfrac hp$(4)
Notice that de Broglie was not suggesting that all matter is governed in some way by electromagnetic waves; de Broglie waves are not electromagnetic waves. We will soon have to come to terms with the true nature of these de Broglie waves but for the moment let us keep this as an open question. Meanwhile, when asked to find the de Broglie wavelength of a material particle (i.e. one having mass), such as an electron, you must take care to calculate λdB using p = mυ, with Ekin = mυ2/2 or, if the particles are travelling at very high speeds, using the equivalent relativistic formulae i; in either case you must not use the expressions for a photon (p = E/c and E = hf).
The de Broglie hypothesis was attractive because it offered an explanation for the mysterious behaviour of electrons in the Bohr model of atomic hydrogen. i Bohr had obtained the correct energy levels for atomic hydrogen by hypothesizing that the single electron was confined to circular orbits of specific radii, and he had determined those radii by assuming that the magnitude of the electron’s angular momentum in each allowed orbit (L = rp) can only be an integer multiple of h/2π. This ‘mysterious’ condition can be obtained by insisting that in any allowed orbit there must be a whole number of de Broglie waves around the circumference of the orbit. In an orbit of radius r, we would then have:
$n\lambda_{\rm dB} = 2\pi r\quad\text{i.e.}\quad\dfrac{nh}{p} = 2\pi r$
implying$\dfrac{nh}{2\pi} = rp = L$ where n = 1, 2, 3, ...(5)
De Broglie’s conjecture that all particles may be associated with waves was a critical breakthrough in understanding the world at the atomic scale. All waves can be diffracted, so to make the proposal plausible it was sufficient to show that beams of particles, electrons say, could be diffracted just like beams of light.
As you will see in Subsection 2.4, this was soon done. However, such was the pace of development that even before this was achieved the association between waves and particles was put onto a firmer mathematical footing by Erwin Schrödinger (1887–1961) and the physical significance of the waves was elucidated by Max Born (1882–1970).
In the rest of this module we will continue to use the term de Broglie wave when referring to the wave aspect of a particle, even when dealing with issues that should more properly be credited to Schrödinger or Born. Their particular contributions are discussed in detail elsewhere in FLAP.
2.3 Review of waves and diffraction
Study comment This subsection reviews some basic ideas of wave motion and wave diffraction through apertures, which will be required later in the module. If you are already clear about these concepts, you can skip straight to Subsection 2.4. If you find that you need further revision after reading Subsection 2.3, the FLAP modules dealing with these topics can be found through the Glossary.
- 1
-
The relationship between the wavelength λ, frequency f and speed of propagation (or wave_groupwave speed) υ of a wave is given by
υ = f λ(6)
- 2
-
The quantity σ = 1/λ is called the wavenumber, and represents the number of wavelengths per unit distance along the direction of propagation. A related quantity is the angular wavenumber, k = 2πσ, i which is related to the wavelength by
$k = \dfrac{2\pi}{\lambda}$(7)
- 3
-
The amplitude of a wave is the magnitude of its maximum displacement from the mean position.
- 4
-
The intensity of a wave is often a measure of the energy delivered in unit time through unit area perpendicular to the direction of propagation. For all waves, the intensity is proportional to the square of the amplitude:
intensity ∝ (amplitude)2(8)
- 5
-
When waves occupy extended regions in two or three dimensions the points at which the wave disturbance is a maximum (or a minimum) at any instant may form straight parallel lines (in two dimensions) or flat parallel planes (in three dimensions), perpendicular to the direction of propagation. Waves that satisfy this condition are said to be plane waves.
- 6
-
Waves encountering an aperture or opening that is narrow compared to their wavelength tend to spread out after passing through that aperture. This phenomenon is called diffraction.
- 7
-
If two or more waves pass through the same region of space at the same time they will interfere according to the principle of superposition. That is, their combined effect at any point will be equal to the sum of the disturbances caused by the individual waves at that point. i
- 8
-
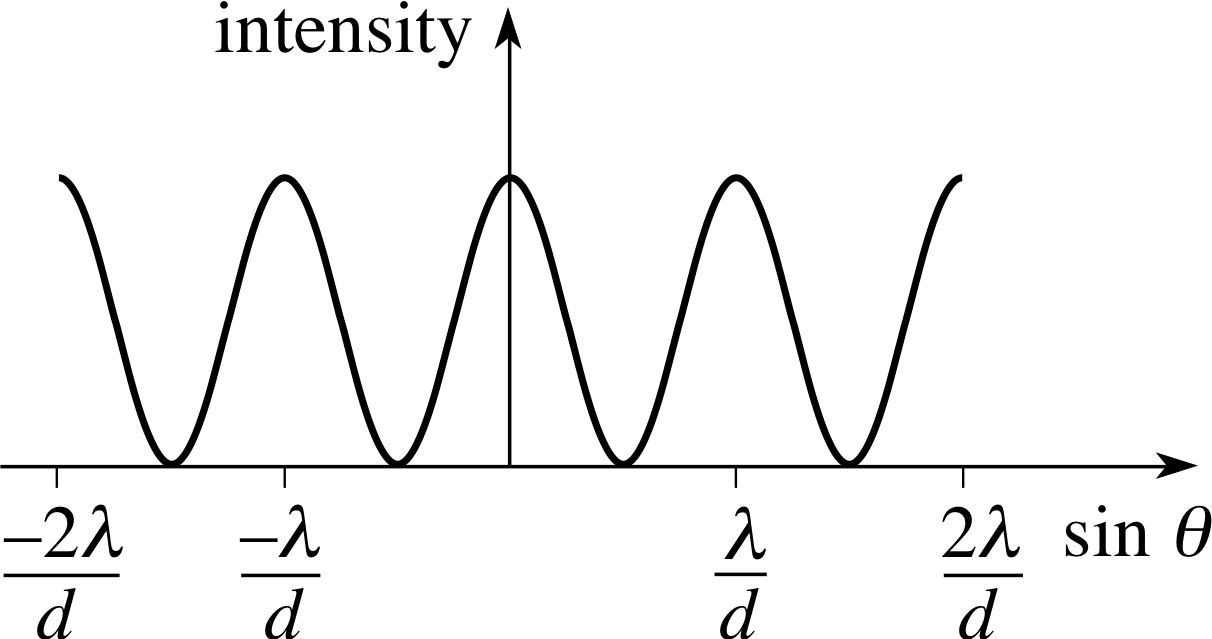
Figure 1 Variation of intensity with angle for a plane wave of wavelength λ passing through a pair of narrow (width ≈ λ) slits of separation d.
Plane waves of wavelength λ encountering a pair of narrow (width ≈ λ) slits, separated by a distance d, in a plane perpendicular to the direction of propagation are diffracted and interfere to produce an interference pattern of varying intensity. Positions of maximum intensity occur at angles θn relative to the original direction of propagation such that
$\sin\theta_n = \dfrac{n\lambda}{d}$(9a)
where n is an integer (0, ±1, ±2, ±3, ...). i
Positions of minimum intensity occur when
$\sin\theta_n = \left(n+\dfrac12\right)\dfrac{\lambda}{d}$(9b)
The variation of intensity with angle is shown in Figure 1.
- 9
-
Plane waves encountering very many narrow parallel slits in a plane perpendicular to the direction of propagation are diffracted and interfere to produce sharp intensity maxima at the same angular positions as for the pair of slits, although the shape of the individual intensity maxima will be more peaked. Such a set of multiple slits is called a diffraction grating.
- 10
-
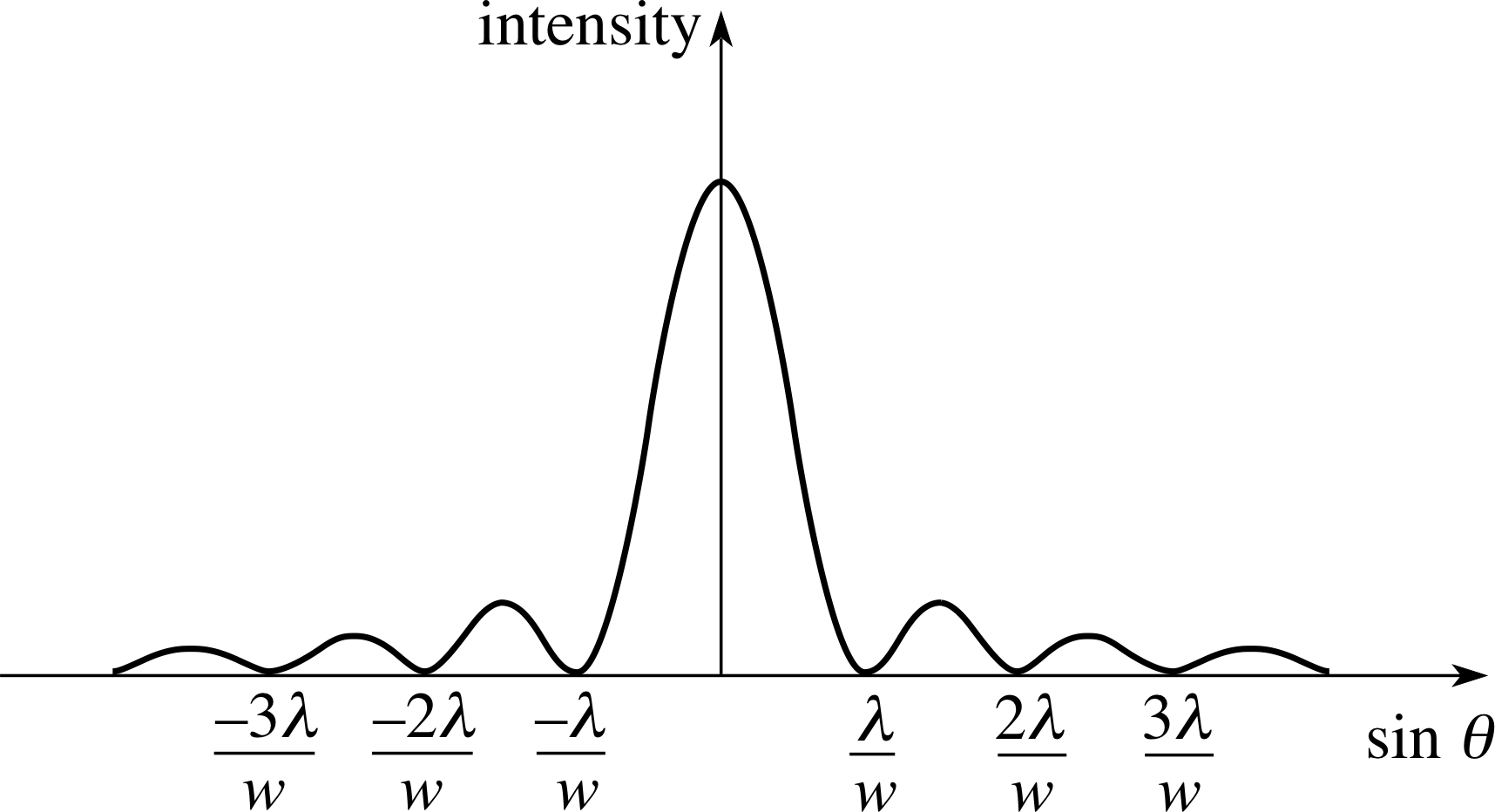
Figure 2 Variation of intensity of the diffracted beam with the sine of the angle of diffraction for plane waves of wavelength λ passing through a single slit of width w.
Plane waves encountering a single aperture of width w are diffracted such that intensity minima occur for angles θn relative to the original direction of propagation given by:
$\sin\theta_n = \dfrac{n\lambda}{w}$(10)
where n is a non–zero integer (±1, ±2, ±3, ...).
The variation of intensity with angle is shown in Figure 2. The central peak has twice the width of the subsidiary peaks, and the subsidiary peaks have a decreasing intensity as their distance from the centre increases.
Question T2
Light of wavelength 5.00 × 10−7 m passes through a pair of narrow slits of separation 0.100 mm. The diffracted beam is incident on a screen which is 2.00 m from the slits and perpendicular to the direction of the original beam. Calculate the distance from the central maximum on the screen to the first two maxima on either side.
Answer T2
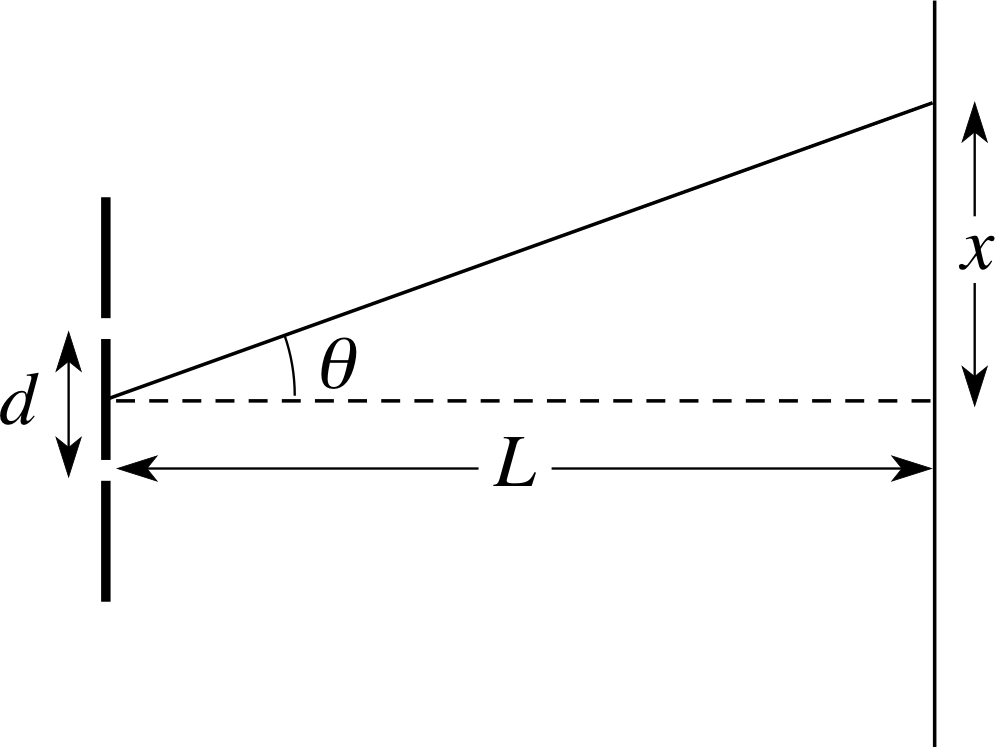
Figure 12 See Answer T2.
For a position of maximum amplitude nλ = d sin θ.
For the arrangement of screen and slits shown in Figure 12,
$\sin\theta = \dfrac{x}{\sqrt{L^2+x^2}}$
For a maximum intensity point on the screen, therefore:
$\dfrac{x}{\sqrt{L^2+x^2}} = \dfrac{n\lambda}{d}\quad\text{and}\quad x^2 = \dfrac{n^2\lambda^2}{d^2}\left(L^2+x^2\right)$
i.e.$x^2\left(1-\dfrac{n^2\lambda^2}{d^2}\right) = \dfrac{n^2\lambda^2}{d^2}L^2$
For a maximum: $x = \dfrac{n\lambda L}{d\sqrt{\left(1-\dfrac{n^2\lambda^2}{d^2}\right)}} = \dfrac{n\lambda L}{\sqrt{d^2-n^2\lambda^2}} \approx \dfrac{n\lambda L}{d}$ (since d ≫ λ)
For n = 1
$x \approx \dfrac{\lambda L}{d} = \rm \dfrac{5.00\times10^{-7}\,m\times2.00\,m}{1.00\times10^{-4}\,m} = 1.00\times10^{-2}\,m$
For n = 2
$x \approx \dfrac{2\lambda L}{d} = \rm \dfrac{2\times5.00\times10^{-7}\,m\times2.00\,m}{1.00\times10^{-4}\,m} = 1.00\times10^{-2}\,m$
Question T3
The experiment described in Question T2 is repeated but using light of a different wavelength. If the first maximum occurs at a position 13 mm from the central maximum, calculate the wavelength of the new light source.
Answer T3
As for the answer to Question T2:
$\lambda \approx \dfrac{dx}{nL} = \rm \dfrac{1.00\times10^{-4}\,m\times1.30\times10^{-2}\,m}{1\times2.00\,m} = 6.50\times10^{-7}\,m$
Question T4
For a plane wave of wavelength λ, what is the minimum slit separation for a diffraction grating that will give a diffraction pattern with n > 0? Why would it be difficult to observe a diffraction pattern with d ≫ λ?
Answer T4
For a diffraction grating, the maximum amplitude signals are observed for the condition: nλ = d sin θ
For d ≪ λ, this condition cannot be met, even for first order diffraction, (n = 1), since it would require sin θ > 1. The minimum d to give first order diffraction for sin θ = 1 is given by dmin = λ. Under these conditions the first order diffracted beam is at 90° to the original direction but will still never reach the screen. Unless d is greater than this, n = 0 is the only order seen.
For d ≫ λ, sin θ is very small, so θ is small and the diffraction maxima overlap, making the diffraction pattern very difficult to observe.
2.4 Verification of the de Broglie hypothesis
From Question T4, it should be apparent that to use a diffraction grating to test the de Broglie hypothesis for, say, electrons, it would have to have a slit separation slightly larger than the expected de Broglie wavelength. Around the time de Broglie made his conjecture, experiments were being done in many physics laboratories using beams of electrically accelerated electrons. Let us see what de Broglie wavelength these would possess.
Question T5
For an electron which has been accelerated from rest through a potential difference of 50 V, calculate (a) the kinetic energy, (b) the momentum magnitude, (c) the de Broglie wavelength.
Answer T5
(a) The increase in the electron’s kinetic energy will be equal to the decrease in its potential energy:
Ekin = ∆Ekin = −∆Epot = e∆V = 1.6 × 10−19 C × 50 V = 8.0 × 10−18 J
(b) Since Ekin = p2/2m
$p = \sqrt{\smash[b]{2m_{\rm e}E_{\rm kin}\os}} = \rm \sqrt{\smash[b]{2\times9.1\times10^{-31}\,kg\times8.0\times10^{-18}\,J}} = 3.8\times10^{-24}\,kg\,m\,s^{-1}$
(c) $\lambda_{\rm dB} = \dfrac hp = \rm \dfrac{6.6\times10^{-34}\,J\,s}{3.8\times10^{-24}\,kg\,m\,s^{-1}} = 1.7\times10^{-10}\,m$
To produce measurable diffraction for the de Broglie wavelength calculated in Question T5, the diffraction grating would need a slit separation of about 10−10 m. Fortunately, nature provides us with an ideal diffraction grating for this experiment – in the form of a crystalline solid.
Such a solid consists of a regular array of atoms and it is possible to show that such an array can produce diffraction effects similar to those of a diffraction grating. In this case the interference occurs between waves reflectionreflected from parallel planes of atoms in the crystal rather than between waves passing through parallel slits, but the principle is the same.
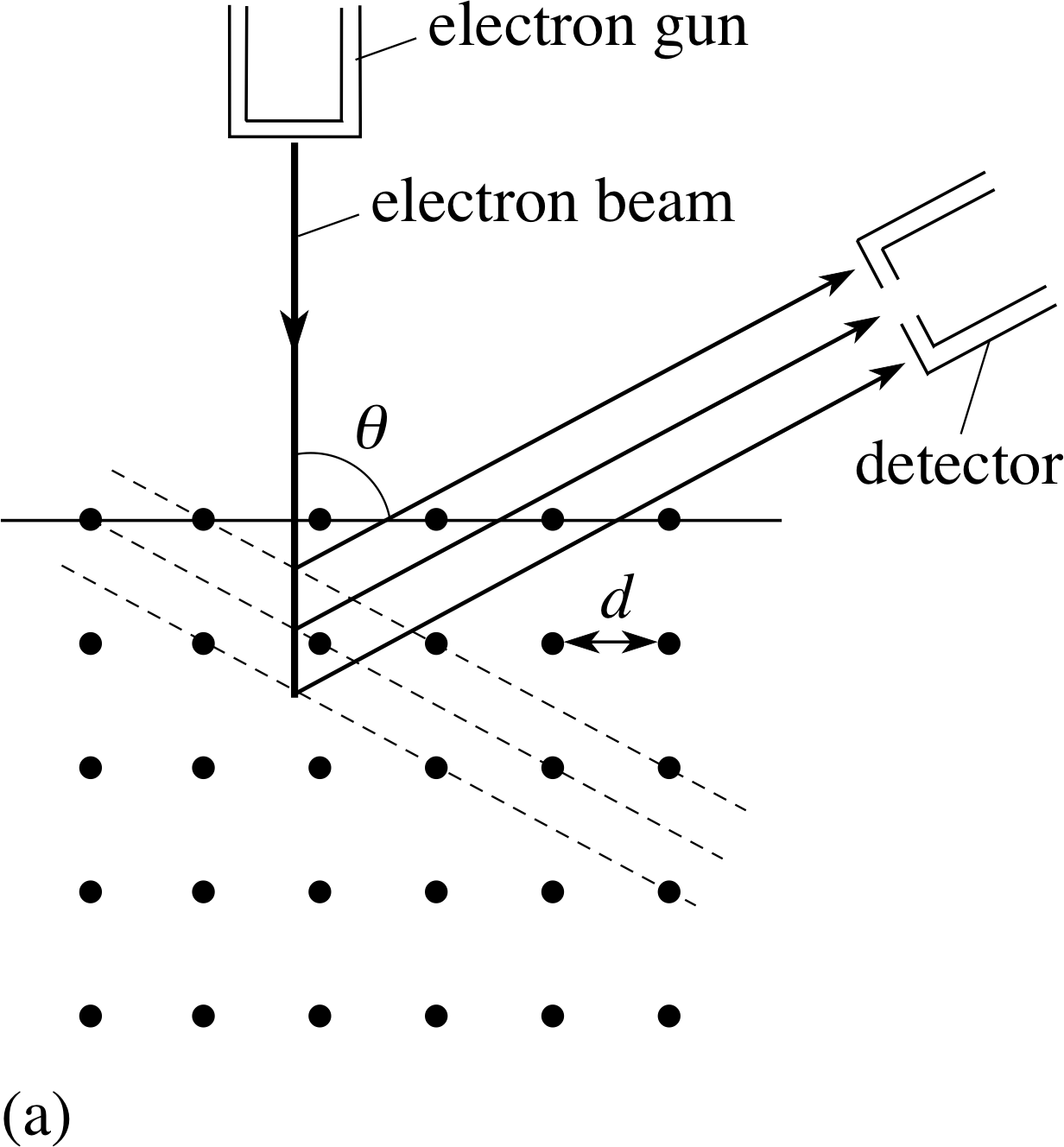
Figure 3 (a) Electrons undergoing diffraction by planes of atoms within a nickel crystal. Individual atoms are shown as dots; the reflecting planes are shown as dashed lines.
Figure 3b Electron diffraction pattern from a nickel target produced by Davisson and Germer.
In 1927, an experiment was carried out by two American scientists, Clinton H. Davisson (1881–1958) and Lester H. Germer (1896–1971) in which they directed a beam of electrons, accelerated through about 50 V, at a crystalline sample of nickel. For the experimental arrangement used, Equation 9a,
$\sin\theta_n = \dfrac{n\lambda}{d}$(9a)
still applies although d is now the interatomic spacing and θ is the angle between the incident and reflected beams as shown in Figure 3a. Davisson and Germer’s experiment gave clear diffraction maxima and hence they were able to calculate a value for λ.
Their result was in good agreement with the predicted de Broglie wavelength. Some of their typical results are shown in Figure 3b. i
Question T6
In a Davisson and Germer experiment, giving the results shown in Figure 3b, the electrons were accelerated through 54 V and the first order intensity maxima (corresponding to n = 1) were from atomic planes separated by 2.15 × 10−10 m. Test whether these results support the de Broglie hypothesis. Assuming this is the first experiment to give such results, what other experiments would you next carry out to confirm your initial impression?
Answer T6
As shown in the answer to Question T5, the magnitude of the momentum of an electron accelerated through V volts is
$p = \sqrt{\smash[b]{2m_{\rm e}\,eV\os}}$ and so $\lambda_{\rm dB} = \dfrac hp = \dfrac{h}{\sqrt{\smash[b]{2m_{\rm e}\,eV\os}}}$
$\lambda_{\rm dB} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{\sqrt{\smash[b]{2\times9.11\times10^{-31}\,kg\times1.60\times10^{-19}\,C\times54\,V}}} = 1.67\times10^{-10}\,m$
First order diffraction occurs for sin θ = λ/d, so the expected angle θ is
$\rm \arcsin\left(\dfrac{1.67\times10^{-10}\,m}{2.15\times10^{-10}\,m}\right) = \arcsin(0.777) = 51°$
(this is only 1% away from the measured result 50.35°)
In order to test the hypothesis further, one might wish to carry out a range of experiments under different circumstances - perhaps changing the values of λ by altering the kinetic energy of the electrons or changing d by using different crystals.
Davisson and Germer’s experiment was the first to show particle diffraction. Since then many experiments have been carried out with many different kinds of particle. The result is always the same – all particles, irrespective of charge, mass, shape or composition, produce a diffraction pattern in agreement with de Broglie’s theory. We are forced to conclude that all particles do indeed have an associated de Broglie wave, that the wavelength of this wave is determined by the momentum of the particle, and that this wave can be diffracted by slits or apertures of an appropriate size.
3 The wave nature of matter
It is all very well to say ‘a beam of particles is diffracted’, but what does that mean as far as individual particles are concerned? What is the nature of these de Broglie waves? Moreover, how does their diffraction influence the relative likelihood of observing an electron at a particular position? We are used to thinking of a wave as a disturbance propagating through some medium – for example, sound waves propagating through air or ripples propagating across the surface of a pond. Even with electromagnetic waves, which require no material medium, there is a disturbance in electric and magnetic fields which propagates.
Can de Broglie waves be thought of in this way? If so, what is the nature of the disturbance? It is here that the subtlety of quantum physics begins to bite!
3.1 The nature of de Broglie waves
Figure 4 Arrangement for the thought experiments.
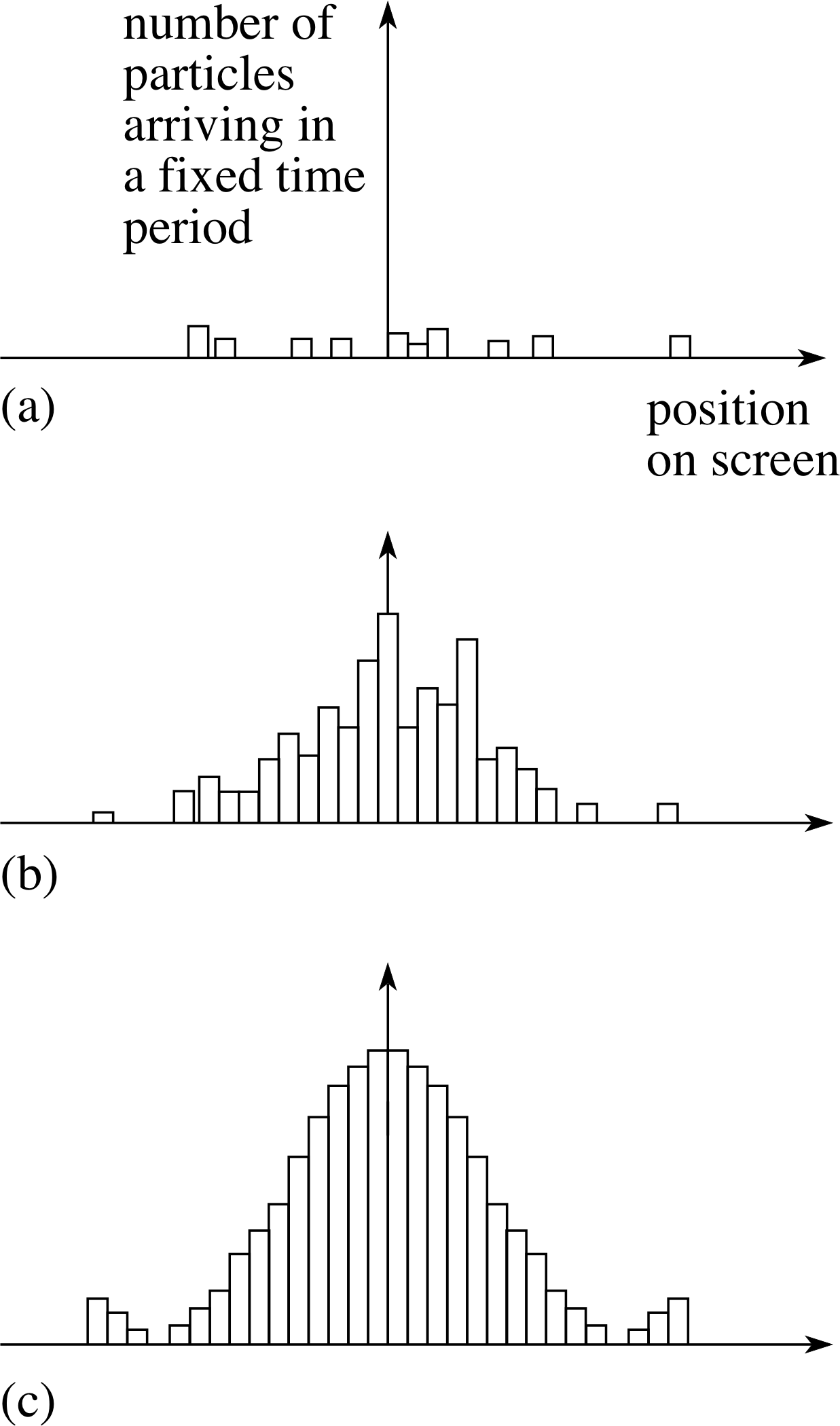
Figure 5 The build up of the diffraction pattern for a single slit as the time elapsed increases from (a) to (c).

Figure 2 Variation of intensity of the diffracted beam with the sine of the angle of diffraction for plane waves (b) of wavelength λ passing through a single slit of width w.
The best way to approach these questions is to think more deeply about the kind of diffraction experiment described in the previous section. However, if we take an experiment such as the one performed by Davisson and Germer, there is a danger we will get lost in the technical details. To avoid this, we introduce the idea of a thought experiment. A thought experiment is simply an experiment which you think through in your head rather than carry out in the laboratory. Thought experiments are a useful way of examining the consequences of a hypothesis in an idealized or simplified setting. They have proved invaluable in the development of quantum theory because of the difficulty and expense of designing ‘real’ experiments in the laboratory. The only warning is that they have to be based on well understood physical principles or on the results of similar experiments which have already been performed.
The ‘equipment’ needed for the thought experiments we wish to consider consists of some kind of gun which fires particles at a pair of slits of width w and separation d in a solid barrier perpendicular to the direction of movement of the particles. The gun is far enough away that particles may pass through either slit and travel on approximately parallel paths. On the far side of the barrier, some distance away, is a screen which consists of a series of particle detectors or ‘bins’ which register each particle as it arrives. The whole arrangement is shown in Figure 4.
Thought experiment 1
Let us start the first of our thought experiments with only one of the slits shown in Figure 4 open, slit A say, and fire particles sufficiently infrequently that we can see where individual particles arrive at the screen. What do we see?
Initially, there seems to be no order. Particles hit the screen in an apparently random fashion. But gradually, as more and more particles arrive, a pattern emerges showing a series of maxima and minima, as in Figure 5. We knew this will occur since Davisson and Germer’s experiment showed that the electrons behave like waves, and we know that waves passing through a slit produce a diffraction pattern like that in Figure 2.
What does this tell us about the nature of a de Broglie wave? Compare Figure 5c with the central part of Figure 2. Both patterns have exactly the same form since they both show a diffraction pattern at a single slit. In Figure 2, the variable plotted on the y–axis is the intensity of the wave; in Figure 5, it is the number of particles arriving in a fixed time.
It appears, therefore, that the nature of the de Broglie wave is such that its average intensity across any small region is proportional to the rate at which particles arrive in that region. Now, as there doesn’t seem to be any order about which particles go where, we can rephrase this in terms of the probability of the arrival of an individual electron in a region.
The average intensity of the de Broglie wave in any small region is proportional to the probability of a particle arriving in that region:
probability ∝ intensity
If we combine this with the general wave result in Equation 8,
intensity ∝ (amplitude)2(Eqn 8)
we predict that:
The square of the amplitude of the de Broglie wave is proportional to the probability of a particle arriving:
probability ∝ intensity ∝ (amplitude)2(11)
Question T7
For a de Broglie wavelength of 1 unit, a slit width of 2 units and a slit separation of 10 units, calculate the position of (a) the central maximum and (b) the first minimum for particles fired through slit A in Figure 4 if the distance between the slit and detection screen is 100 units. Sketch the pattern on a graph of intensity against x (the position on the screen).
[Hint: Use the answer from Question T2 without the approximation that d ≫ λ.]
Answer T7
(a) The central maximum will be directly opposite slit A. That is 5 units from the centre of the screen.
(b) From Equation 10,
$\sin\theta_n = \dfrac{n\lambda}{w}$(Eqn 10)
the position of the first minimum is given by
$\sin\theta_1 = \dfrac{\lambda_{\rm dB}}{w}\quad\text{but}\quad\sin\theta_1 = \dfrac{x_1}{\sqrt{\smash[b]{L^2+x_1^2}}}$
where L is the distance from slit to screen and x1 is the position of the first minimum on the screen measured from the central maximum.
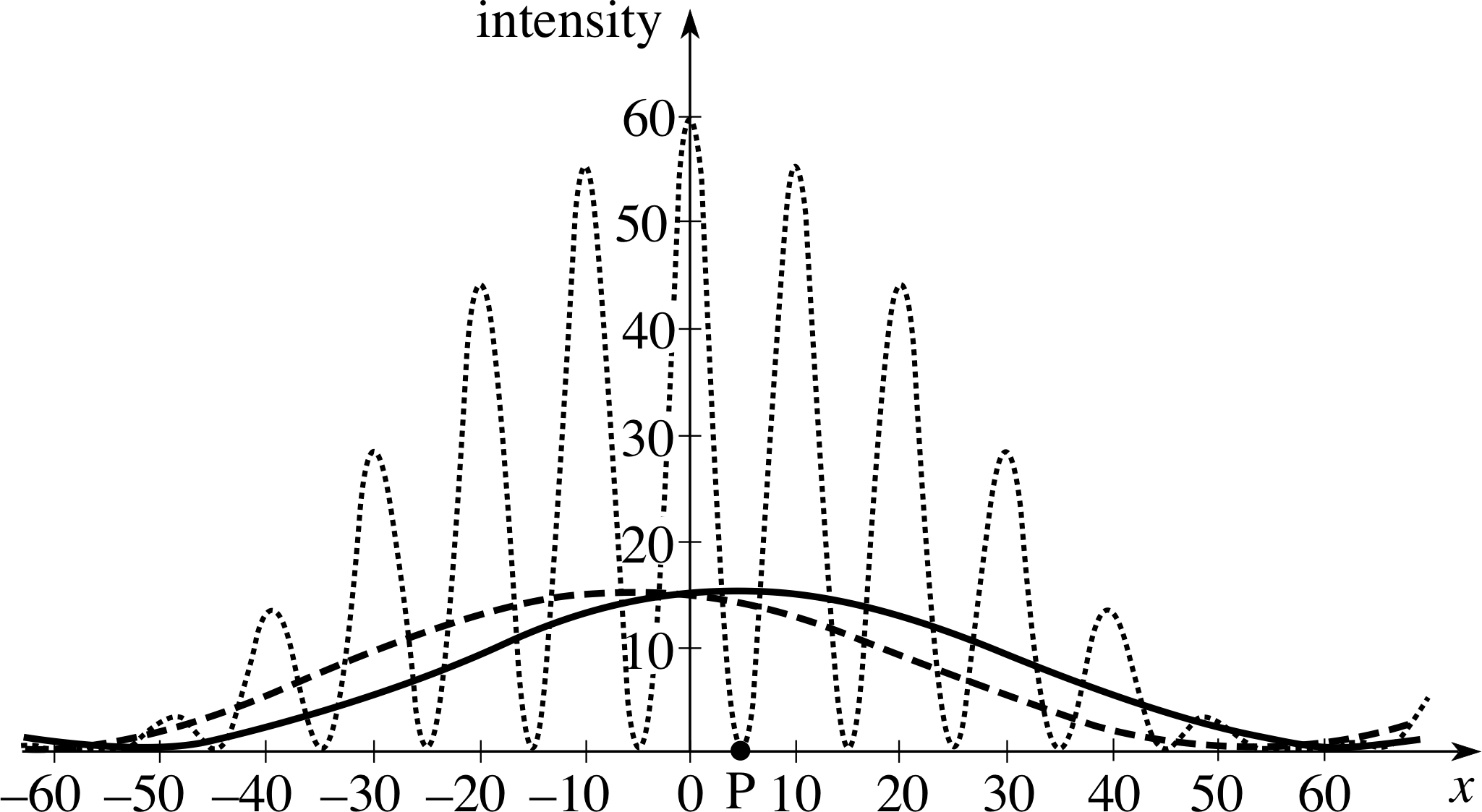
Figure 6 The diffraction patterns for the situations described in Questions T7 to T9. The dashed line is for slit A open; the solid line is for slit B only open and the dotted line is for both slits open. (The intensity units in this figure are arbitrary.)
So$\dfrac{\lambda_{\rm dB}}{w} = \dfrac{x_1}{\sqrt{\smash[b]{L^2+x_1^2}}}\quad\text{or}\quad\dfrac{\lambda_{\rm dB}^2(L^2+x_1^2)}{w^2} = x_1^2$
i.e.$x_1^2\left(1-\dfrac{\lambda_{\rm dB}^2}{w^2}\right) = \dfrac{\lambda_{\rm dB}^2}{w^2}L^2$
Thus$x_1^2(w^2-\lambda_{\rm dB}^2) = \lambda_{\rm dB}^2L^2$
i.e.$x_1 = \dfrac{\lambda_{\rm dB}L}{\sqrt{\smash[b]{w^2-\lambda_{\rm dB}^2}}} = \dfrac{1\times100}{\sqrt{2^2-1^2}} = \rm 58\,units$
Together with the 5 unit displacement of the centre maximum this places this first minimum at −63 units and +53 units.
The variation of intensity with position is shown by the dashed line in Figure 6.
The trouble with this interpretation of the de Broglie wave is that it only tells us about probabilities. We can work out the probability that any particle will be deflected by a given amount as it passes through the slit, but we cannot say exactly what will happen to any individual particle. Let us try one or two more experiments.
3.2 Interference of de Broglie waves
As a precursor to the next thought experiment we will think about what happens if we close slit A and open slit B.
Question T8
What change would you expect in the diffraction pattern from Question T7? Sketch the pattern on the same graph as your sketch for Question T7.

Figure 6 The diffraction patterns for the situations described in Questions T7 to T9. The dashed line is for slit A open; the solid line is for slit B only open and the dotted line is for both slits open. (The intensity units in this figure are arbitrary.)
Answer T8
The pattern will be exactly the same as for slit A - but now centred on the point opposite slit B as shown by the solid line in Figure 6.
Thought experiment 2
Now, for the second thought experiment let us think about what happens if we open both slits.
Question T9
Sketch the pattern (on the same graph as used for Questions T7 and T8) you would expect when both slits are opened for the configuration described in Question T7. (It is particularly important that you check the answer to Question T9 before continuing.)
Answer T9

Figure 6 The diffraction patterns for the situations described in Questions T7 to T9. The dashed line is for slit A open; the solid line is for slit B only open and the dotted line is for both slits open. (The intensity units in this figure are arbitrary.)
In order to get the observed pattern, you must take into account the diffraction through both slits and the interference between the two de Broglie waves. The positions on the screen corresponding to maxima are as given in te answer to Question T2. Without using the approximation d ≫ λ we have:
$x_n = \dfrac{n\lambda L}{\sqrt{d^2-n^2\lambda^2}}$
For n = 1 $x_1 = \rm \dfrac{100}{\sqrt{100-1\os}}\rm units = 10.1\,units$
For n = 2 $x_2 = \rm \dfrac{200}{\sqrt{100-4\os}}\rm units = 20.4\,units$
For n = 3 $x_3 = \rm \dfrac{300}{\sqrt{100-9\os}}\rm units = 31.4\,units$
There will also be points of zero intensity, roughly halfway between these maxima. The pattern is shown by the dotted line in Figure 6, though you will not have been able to predict the peak heights.
The important point to note here is that there is a completely different set of positions of maximum intensity and zero intensity when both slits are open. If we think strictly from a particle viewpoint, a particle passing through slit A appears to be influenced by whether or not slit B is open. With slit B open there are a number of positions of zero intensity where it definitely will not arrive which had a high probability of arrival when slit B is closed – so there are some places on the screen where the probability of arrival is decreased if the second route is opened up! Classical physics cannot explain these observations but it is just what we would expect if de Broglie waves are to behave as other waves and produce interference effects as well as diffraction effects.
You may well have answered Question T9 by saying that as each particle only passes through one slit, that particle cannot possibly be influenced by the condition of the other slit. Therefore at any point on the screen the total number of arrivals with both slits open is just the sum of the number of arrivals from the individual slits. The ‘two-slit’ diffraction pattern would then just be the sum of the single slit patterns. Yet, as Answer T9 shows, this is completely incorrect!

Figure 6 The diffraction patterns for the situations described in Questions T7 to T9. The dashed line is for slit A open; the solid line is for slit B only open and the dotted line is for both slits open. (The intensity units in this figure are arbitrary.)
Figure 6 summarizes the intensity patterns on the screen for these experiments. i You can see there are a number of positions such as P which have quite a high probability of a particle arriving if only one slit is open but zero probability of an arrival when both slits are open. In terms of the old particle view of the world, this result is truly remarkable. It appears as if the particles which pass though one slit ‘know’ whether or not the adjacent slit is open! i
The important point to grasp here is that the results correspond exactly with what would be expected from the behaviour of a wave, but they are inexplicable in terms of the previously understood behaviour of particles. Of course we should not abandon the ‘old’ ideas without a fight and, indeed, many extremely intelligent scientists have expended a great deal of effort in trying to find a way of explaining such phenomena in terms of classical physics.
So far no explanation has been successful – but let us look at two of the more plausible attempts, anyway.
Attempt 1 Some particles collide with the sides of the slit as they go through and these are the ones which are deflected away from the original direction. They bounce off according to Newton’s laws and, if we had enough information, we could predict the path of individual particles.
Attempt 2 Particles collide with each other after passing through the slits. This is why the result of Experiment 2 is not just the sum of single slit patterns like Experiment 1.
We can easily set up an experiment to test Attempt 2 as follows:
Thought experiment 3
We will slow down the rate of firing of the particle gun so that every particle arrives at the screen before the next one is released. When we do this, we find no change in the experimental results except of course that there are now fewer arrivals in any time interval. So, the two slit pattern is not the result of particles colliding with each other and the diffraction effect works for individual particles. i
How about the particles colliding with the sides of the slit? Maybe we can at least explain the single slit experiments in this way. First think about what a collision means. The particle must interact with the atoms that make up the barrier housing the slits. This interaction should determine exactly how the particle is deflected. Now if this were true, we should expect that the deflections would be influenced at least to some extent by the nature of the particles themselves and the material of the barrier. For example the interaction would depend on the mass of the barrier atoms and how strongly they are held in place. It should also matter whether or not the particles are charged. Yet, as observed earlier, the main features of the diffraction patterns only depend on the particles’ de Broglie wavelength and the slit width and not on any other properties of the barrier or the particles.
Let us not give up completely yet. Suppose we try to follow an individual particle and see what happens to it. We could do this if we knew exactly where it entered the slit and its direction of motion.
Thought experiment 4
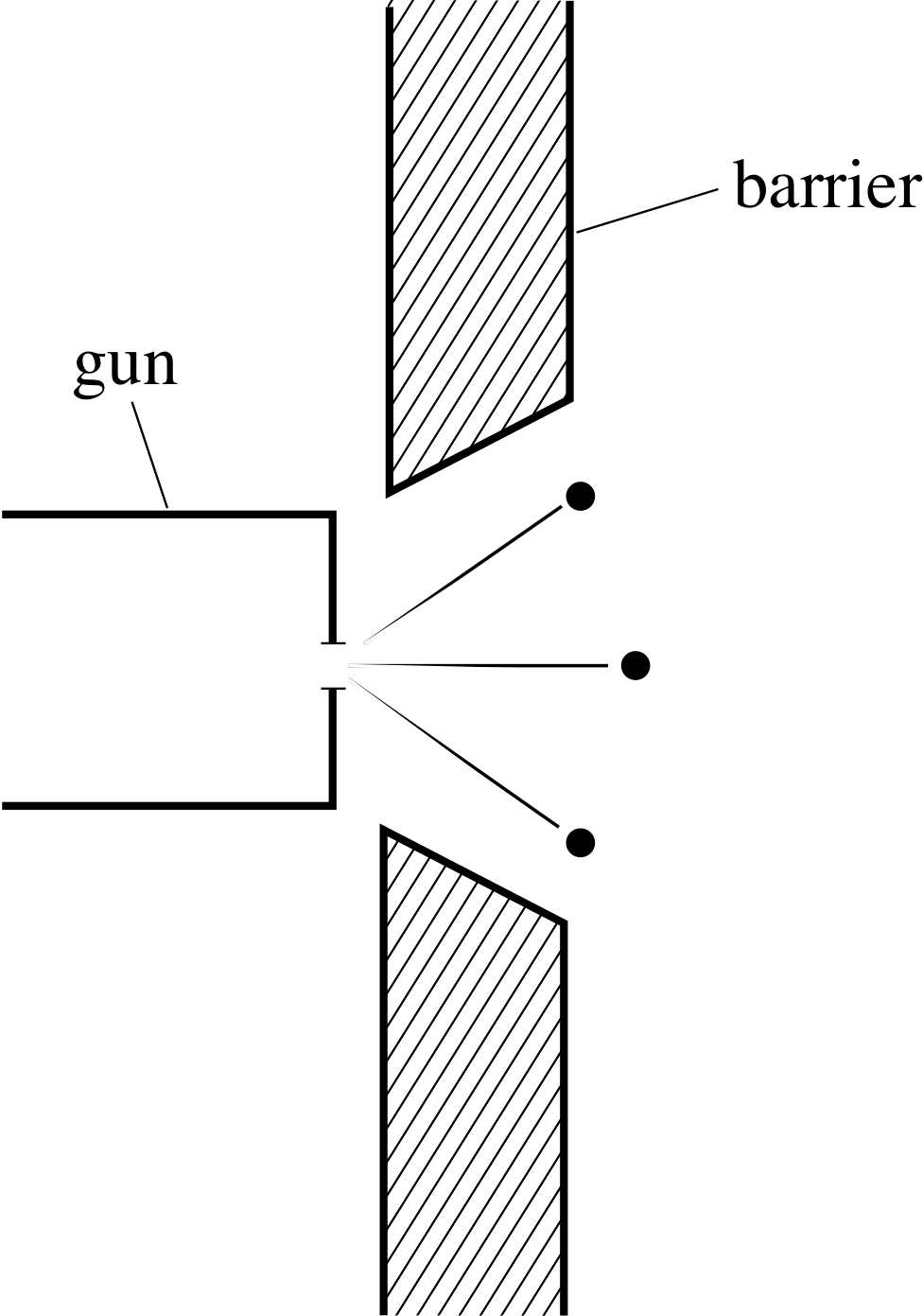
Figure 7a A gun with a small aperture is brought close to the slit – the position at which a
We can specify where it enters the slit by making the mouth of the gun very small and bringing it very close to the slit as in Figure 7a. Now, can we also specify the exact direction of motion of the particle?
✦ From what you have learnt so far, what is the effect of the width of the mouth of the gun on the direction of the particles?
✧ The mouth of the gun is, in effect, a slit, so it too will diffract the waves associated with the particles and cause them to spread out. From Equation 10,
$\sin\theta_n = \dfrac{n\lambda}{w}$(Eqn 10)
the smaller the width of the gun mouth, the greater will be the spread of the diffraction pattern. Consequently, if we reduce the width of the gun mouth, we will know more about the position at which the particle enters the slit, but we will know less about the direction of motion of the particle.
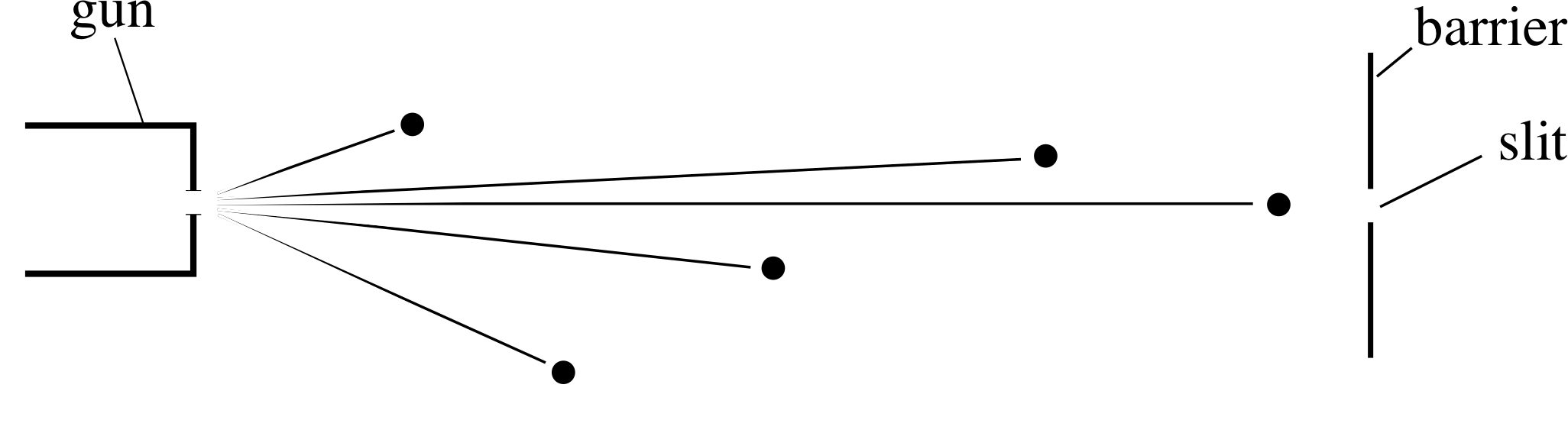
Figure 7b The gun is taken far away from the slit. Now the direction of motion of the particles is specified but not the point at which they enter the slit.
Foiled again! Let us try a different tack. We can specify the direction by taking the gun back a very long way from the slit. Now all particles which pass through the slit must be travelling parallel to each other along the line joining the slit and gun as in Figure 7b.
The problem now is that we can’t say exactly where individual particles enter the slit! It seems we can’t win; it isn’t possible to specify exactly where a particle enters the slit and its directions of motion at the same time. This statement contains the seed of a very profound truth, called the Heisenberg uncertainty principle, to which we will return in Section 4.
3.3 The wave nature of matter and the everyday world
The above attempts to explain these experimental results by the classical laws of physics don’t work. The same is true of all the other classical explanations which have been proposed in the last 70 years. We are left with a simple yet disturbing picture. Every particle can be associated with a wave, the intensity of which at any point determines the probability of finding the particle there. The motion of every particle through space is thus dependent on the behaviour of the de Broglie wave. It is the de Broglie wave rather than the particle which passes through both slits in the above experiments and it is the diffraction and interference of the wave which governs the probability of the subsequent direction of travel of the particle.
If you find these ideas somewhat difficult to accept you are not alone. Everyone who learns about quantum theory struggles to come to terms with it. The great physicist, Niels Bohr once said, ‘If you aren’t confused by quantum physics, you haven’t really understood it.’
Why do we find it so strange? It is because when we try to understand things, we usually try to think of models and analogies from the everyday world. Thus, if we say ‘Electrons interact with each other like tiny ping–pong balls,’ that is acceptable because we can all imagine ping–pong balls colliding. If we say ‘Electrons are like water waves,’ that is also easy to understand because we have all seen water waves. The problem is that electrons and other quanta are like nothing we experience in the everyday world and sometimes we have to use the image of particles and sometimes the image of waves to predict what they are going to do.
If we now ask ‘Why don’t quantum phenomena occur in the everyday world?’ The answer is that they almost certainly do but the effects are usually so incredibly tiny that they are impossible to observe. i Consider the following question.
Question T10
Estimate the angle corresponding to the first diffraction minimum when you leave your house through the front door. If you assume that typically you are ‘diffracted’ through about half of that angle, how far would you have to travel before your path would have deviated from the straight through path by 1 cm?
Answer T10
Assuming a mass of 60 kg and a speed of 1 m s−1, Equation 4,
$\lambda_{\rm dB} = \dfrac hp$(Eqn 4)
gives a de Broglie wavelength of
$\lambda_{\rm dB} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{60\,kg\times1.0\,m\,s^{-1}} = 1.1\times10^{-35}\,m$
From Equation 10 (and taking the door width to be 1 m),
$\sin\theta_n = \dfrac{n\lambda}{w}$(Eqn 10)
$\sin\theta_1 = \dfrac{\lambda}{w} = \rm \dfrac{1.1\times10^{-35}\,m}{1\,m} = 1.1\times10^{-35}\,m$
andθ1 = 1.1 × 10−2 rad
So a ‘typical’ diffracted angle would be ≈ 5 × 10−36 rad.
For a deviation x in a distance D, $\theta \approx \sin\theta \approx \dfrac xD$
so$D = \dfrac{x}{\sin\theta} = \rm \dfrac{1\times10^{-2}\,m}{5\times10^{-36}} = 2\times10^{33}\,m$
As this is about 107 × the distance to the edge of the observable Universe it is hardly surprising we don’t ‘feel’ diffracted as we walk through a door!
The answer to Question T10 demonstrates that there is no contradiction between quantum theory and the everyday world. Exactly the same laws of physics apply on all scales. The only difference is that at very small scales, wave effects are significant; on a macroscopic scale, they are usually unobservable. Notice that it is the small size of Planck’s constant that makes the wave effects insignificant on a macroscopic scale. If h were much larger, we would be living in a very different Universe! i
Question T11
Repeat Question T10 with a value for h of 6.6 J s. What effect would this have on everyday life?
Answer T11
As in Question T10, but with h = 6.6 J s, we find λdB = 0.11 m.
sin θ1 = λdB/w = 0.11 m/1 m = 0.11 so θ1 = 6.3°
D = (1 × 10−2 m)/(0.05) = 0.2 m or 20 cm
Diffraction of people and other macroscopic objects would be very apparent! Of course with such a value for Planck’s constant, the Universe would have developed in a very different way, so the question as to the effect on everyday life is somewhat meaningless.
However, you could amuse yourself for a few minutes by speculating on the effects of a sudden change in h to 6.6 J s. Mundane tasks such as driving a car into a garage or pouring water out of a kettle or playing snooker, would be more of a challenge. For example, would it be better or worse to reduce the speed in these tasks?
4 The Heisenberg uncertainty principle
We now return to the point raised in Subsection 3.2, when we pointed out that it seemed to be impossible to specify precisely both the particle’s position relative to the slit and its direction of motion at the same time. We will show that this is just an example of a general principle which says that it is impossible to have complete, simultaneous knowledge of the position of a particle and its momentum. Once again, this is a bizarre statement if we insist in trying to think in terms of classical particle physics but you will see that it arises naturally as a consequence of the wave nature of matter.
4.1 Position and momentum for de Broglie waves
As with the thought experiments in Section 3, we can go a long way by carefully considering the simplest situations. We can start with a particle moving in one dimension (in the x–direction). We will imagine that it is a free particle in the sense that it is experiencing no net force – and we will consider measurements of its position x (which we can find from the de Broglie wave amplitude) and its momentum px, which is related to the de Broglie wavelength.
First let us consider a particle whose momentum we know exactly. That is to say, we have some means of measuring the momentum px at some instant in time with arbitrarily high accuracy. i
✦ What can we say about the de Broglie wavelength of the particle at the time we make the measurement?
✧ From Equation 4,
$\lambda_{\rm dB} = \dfrac hp$(Eqn 4)
if we know the momentum px exactly, the wavelength is also exactly defined as λ = h/px.
Now, it is a property of wave motions in general that a wave travelling along the x–axis with an exactly defined wavelength must be infinite in extent (i.e. it must extend to ±∞) with the same amplitude everywhere. A perfect sinusoidal wave is a good example of this. If the amplitude of the de Broglie wave is the same everywhere, then the probability of finding the particle must be the same everywhere because the probability is related to the amplitude squared. In other words, we have no idea whatsoever about the position of the particle! i
This doesn’t seem very realistic because we usually have some idea of where particles are located – they are to some extent localized particles. For example, the paper on which this module is printed contains billions of atoms but even though they are jiggling about with thermal energy, the position of a given atom will be fixed to within a few nanometres. i
How can we picture the de Broglie wave of a localized particle? Still thinking of the one–dimensional situation, if we know that the particle is within a particular range ∆x, it follows that the probability of finding the particle outside ∆x will be vanishingly small. From Equation 11,
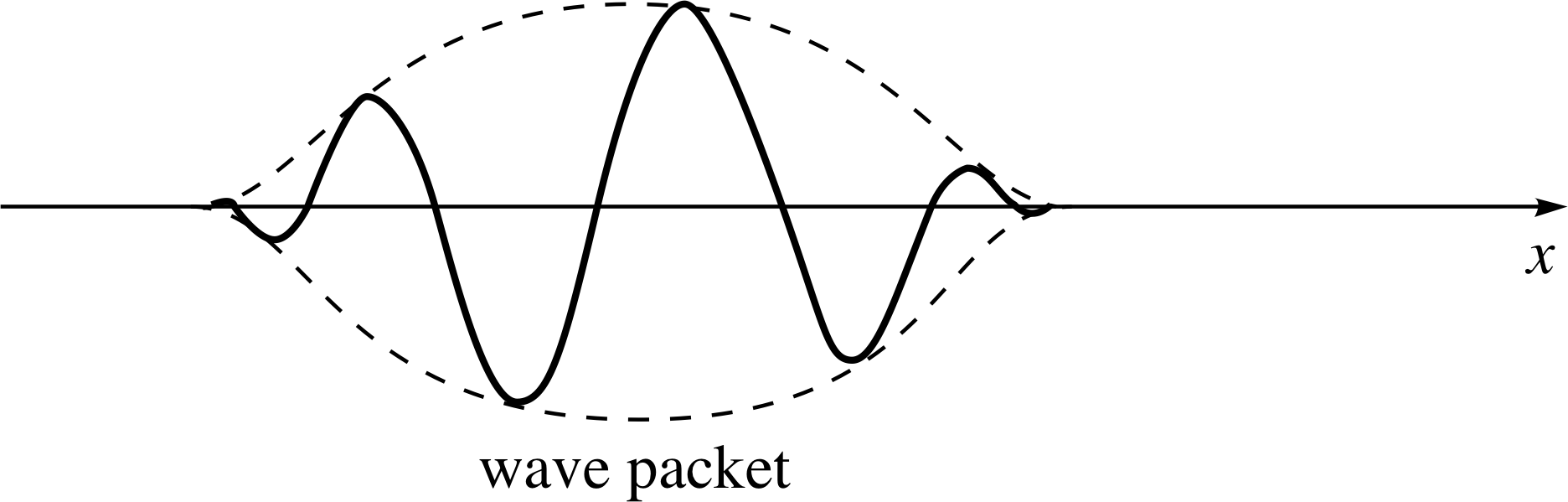
Figure 8 A ‘snapshot’ of a de Broglie ‘wave packet’ representing a localized particle.

Figure 9 A ‘wave packet’ produced by adding together eight infinite waves (ψ1 to ψ 8) according to the principle of superposition.
probability ∝ intensity ∝ (amplitude)2(Eqn 11)
we know that the probability is proportional to the square of the amplitude of the de Broglie wave, so the amplitude must go to zero where there is no chance of finding the particle. In that case, we are left with a finite wavetrain or a wave packet to represent a localized particle, as shown in Figure 8.
It is possible to show that a wave packet can be produced mathematically by a superposition of infinitely long waves with differing wavelength, amplitude and phase. Figure 9 shows how we might start to achieve this by superposing eight separate waves ψ1,ψ2, ... ψ8. The interference between the eight waves produces a combined wave which tails off to zero in the desired manner. With just the eight component waves of Figure 9 we don’t actually obtain zero amplitude everywhere outside the region ∆x.
However, by using a mathematical technique called Fourier analysis it can be shown that a wave packet of length ∆x can be produced by superposing a continuous band of waves covering a limited wavelength range.
Aside To ‘add together’ an infinite number of component waves over a continuous range of wavelengths it is necessary to evaluate a definite integral of the form
$\displaystyle \int^{\lambda_0+\Delta\lambda}_{\lambda_0-\Delta\lambda}a(\lambda){\it\psi}(x,t,\lambda)\,d\lambda$
This is beyond the scope of this module.
The most convenient way to express this result is in terms of the range of angular wavenumber rather than wavelength. Recall from Subsection 2.3 that the angular wavenumber k of a wave of wavelength λ is defined as:
$k = \dfrac{2\pi}{\lambda}$(Eqn 7)
Fourier analysis shows that in order to produce a wave packet of length ∆x we must combine waves with wavenumbers k that cover a range from k0 to k0 + ∆k where k0 is some (unimportant) constant and ∆k satisfies the condition:
∆x∆k ≈ 1(12)
Equation 4,
$\lambda_{\rm dB} = \dfrac hp$(Eqn 4)
and Equation 7 give the relation between momentum magnitude and angular wavenumber as:
$p = \dfrac{hk}{2\pi} = \hbar k$(13)
where we have written $\hbar$ for h/2π, a quantity which appears frequently in quantum mechanics. (The symbol $\hbar$ is read as ‘h-bar’.)
It follows that for a particle moving in the x–direction, represented by a superposition of waves also travelling in that direction:
$\Delta p_x = \dfrac{h}{2\pi}\Delta k = \hbar\Delta k$
Substituting for ∆k from Equation 12 we have
$\Delta p_x \approx \dfrac{\hbar}{\Delta x}$
which can be rearranged to give
$\Delta p_x\,\Delta x \approx \hbar$(14a)
This equation was first formulated in 1927 by the German physicist Werner Heisenberg (1901–1976) and is a limiting case of what is now known as the Heisenberg uncertainty principle. Notice that it agrees with our earlier assertion – that if the momentum is known exactly, then we can have no knowledge whatsoever about the particle’s position (i.e. if ∆px = 0, then $\Delta x \approx \hbar/0$ is undefined).
Note A more rigorous treatment and a careful specification of what is meant by the uncertainties ∆x and ∆px gives $\hbar/2$ rather than $\hbar$ on the right–hand side of Equation 14a, but we will not be concerned about this detail here.
Question T12
If we know the position of a particle exactly, what can we say about its momentum?
Answer T12
Equation 14a,
$\Delta p_x\,\Delta x \approx \hbar$(Eqn 14a)
shows that $\Delta p_x = \hbar/\Delta x$.
It follows that if ∆x is zero, ∆px must be undefined – that is we have no knowledge at all about the particle’s momentum.
Note that in deriving Equation 14a nothing was said about how ∆x and ∆px were to be determined. Heisenberg’s limit is a limit in principle which arises directly as a consequence of the wave nature of matter. Equation 14a sets a lower limit on the combined uncertainty of any pair of simultaneous position and momentum measurements in a given direction. The measurement uncertainties ∆x and ∆px can never be better than this limit, but they could be worse. So the Heisenberg uncertainty principle itself is usually written as:
The Heisenberg uncertainty principle $\Delta x\,\Delta p_x \gtrsim \hbar$(14b)
Exactly the same principles apply to three–dimensional motion, where the position and momentum uncertainties in each dimension are independent. We can then add to Equation 14b:
The Heisenberg uncertainty principle $\Delta y\,\Delta p_y \gtrsim \hbar$(14c)
The Heisenberg uncertainty principle $\Delta z\,\Delta p_z \gtrsim \hbar$(14d)
We may express the gist of Equations 14b, c and d in words, as follows:
The Heisenberg uncertainty principle implies that there is a fundamental limit to the accuracy with which we can simultaneously determine the position and momentum of a particle in a given direction. This limit has nothing to do with the methods employed to make the measurements.
While the Heisenberg uncertainty principle is often taken as the fundamental statement of quantum physics it is important to appreciate that it is the de Broglie statement which is the more fundamental. Once the wave representation of a particle is accepted, the Heisenberg uncertainty principle follows inexorably from the mathematics of waves, as given by Fourier analysis.
4.2 The Heisenberg uncertainty principle in action
In this subsection we will try to make clear what we mean by the uncertainty associated with a ‘simultaneous determination of position and momentum’ by the following example.
Consider a free particle travelling along the x–axis of a coordinate system. If it is truly travelling along the x–axis, its y–coordinate will be zero. We can make a measurement to ensure this is the case by placing a barrier perpendicular to the x–axis at a certain point and cutting a slit in the barrier corresponding to the x–axis position. Now the slit must have a certain width, say w. If the particle passes through the slit, it must have passed within ±w/2 of the x–axis at that point. Another way of saying the same thing is that we have knowledge of the y–position of the particle at that point with an uncertainty, ∆y, of w.
✦ What effect will this measurement have on our knowledge of py, the y–component of momentum of the particle?
✧ The Heisenberg uncertainty principle says that now there is an inherent uncertainty in the possible knowledge of py given by $\Delta p_y \approx \hbar/w$.
Thus the narrower the slit, the smaller w becomes and the larger is the uncertainty in py. If w becomes very small, ∆pymay become very large with the result that the particle may have a large component of momentum and may now shoot off on a path which is nowhere near parallel to the x–axis. Of course we cannot predict what the path will be – we can only predict the range of possibilities given by ∆py.
Suppose a beam of many identically prepared particles is fired at the slit. Those which pass through the slit will head off in different directions, consistent with $\Delta p_y = \hbar/w$. In other words, the beam will fan out as it goes through the slit. This should sound familiar! It is our old friend diffraction of a particle beam through a single slit, which was looked at in Subsection 3.1, in thought_experiment_1thought experiment 1. However, this time we have explained it by using the Heisenberg uncertainty principle! There is nothing strange about this, it simply emphasizes the fact that the uncertainty principle itself is simply a manifestation of the wave behaviour associated with particle motion.
4.3 The Heisenberg uncertainty principle and the macroscopic world
As was the case with particle diffraction in Section 3, the Heisenberg uncertainty principle is difficult to swallow because we have no experience of it in the everyday world. We do not find in practice that measurements made on the momentum of a car, say, affect the accuracy with which we can measure its position. It is easy to see why, if we consider a specific example.
Question T13
A 1000 kg car is travelling at 15 m s−1. At a particular time, its position along a certain axis is noted with an uncertainty of ±1.0 mm. Use the Heisenberg uncertainty principle to estimate the minimum possible percentage uncertainty in a momentum measurement made along the same axis at the same time.
Answer T13
From the Heisenberg uncertainty principle (Equation 14a),
$\Delta p_x\,\Delta x \approx \hbar$(Eqn 14a)
the uncertainty ±1.0 mm gives ∆x = 2.0 mm, so the minimum uncertainty in momentum is
$\Delta p_x = \dfrac{\hbar}{\Delta x} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{2\pi\times2.0\times10^{-3}\,m} \approx 5.3\times10^{-32}\,kg\,m\,s^{-1}$
For the car px = mυx = 1000 kg × 15 m s−1 = 1.5 × 104 kg m s−2
The percentage uncertainty is
$\pm\dfrac{100\Delta p_x}{2p_x}\% = \rm \pm\dfrac{100\times5.3\times10^{-32}\,kg\,m\,s^{-1}}{2\times1.5\times10^4\,kg\,m\,s^{-1}}\% = \pm1.8\times10^{-34}\%$
Of course this uncertainty is so much less than the measurement error in any conceivable method of measurement and so it is of no practical concern. The Heisenberg uncertainty principle does not usually have a noticeable effect on the scale of the everyday world.
The answer to Question T13 shows that the limits imposed on accuracy by the Heisenberg uncertainty principle are completely insignificant and unnoticeable in the everyday world. Now consider the situation for a particle moving on an atomic scale.
Question T14
Repeat Question T13 for a hydrogen atom (m = 1.7 × 10−27 kg) travelling at 1000 m s−1 (a typical speed in a gas at room temperature) if the position is known at a certain moment to within about one atomic diameter (roughly 1.0 × 10−10 m).
Answer T14
For the hydrogen atom from Equation 14a,
$\Delta p_x\,\Delta x \approx \hbar$(Eqn 14a)
we find
$\Delta p_x = \dfrac{\hbar}{\Delta x} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{2\pi\times1.0\times10^{-10}\,m} = 1.1\times10^{-24}\,kg\,m\,s^{-1}$
Here px = mHυx = 1.7 × 10−27 kg × 1000 m s−1 = 1.7 × 10−24 kg m s−1
The percentage uncertainty is
$\pm\dfrac{100\Delta p_x}{2p_x}\% = \rm \pm\dfrac{100\times1.1\times10^{-24}\,kg\,m\,s^{-1}}{2\times1.7\times10^{-24}\,kg\,m\,s^{-1}}\% \approx \pm 32\%$
At an atomic scale, the Heisenberg uncertainty principle is very important in determining how accurately position and momentum can be known.
At this scale, the limits imposed by the Heisenberg uncertainty principle are similar in scale to the quantities being measured and quantum physics has a very significant effect.
4.4 Uncertainty in time and energy
The Heisenberg uncertainty principle can be formulated in terms of energy rather than momentum. This is most easily seen for a free particle. In this case, the only energy is kinetic energy, Ekin = mυ2/2, which we may write in terms of momentum magnitude p = h/λ = hk/2π as:
$E = E_{\rm kin} = \dfrac{m\upsilon^2}{2} = \dfrac{(m\upsilon)^2}{2m} = \dfrac{p^2}{2m} = \dfrac{h^2k^2}{8\pi^2m}$(15)
Following the same kind of Fourier analysis approach as before, we end up with another simple relationship:
$\Delta E\,\Delta t \approx \hbar$(16a)
where ∆t is the time it takes the wave packet to go past a particular point. What is the physical interpretation of this? Well, the length of time it takes the wave packet to go past is effectively a measurement of its length. Thus a large ∆t means a long wave packet which, from the last subsection, implies a small uncertainty in momentum and therefore a small uncertainty in energy. Conversely, a small time interval for measurement implies a short wave packet and therefore a large ∆Ekin. Thus for measurement uncertainties, we have:
Heisenberg uncertainty principle $\Delta E\,\Delta t \gtrsim \hbar$(16b)
This can be expressed in words as follows:
The Heisenberg uncertainty principle places a lower limit on the combined uncertainty of an energy measurement and the time taken to make the measurement.
As with the position–momentum relationship, the lower limit imposed by the time–energy formulation of the uncertainty principle is so small that its effects are not apparent in the macroscopic world. At an atomic level it has important consequences, as the following questions demonstrate.
Question T15
For a cyclist travelling at 10 m s−1, estimate the time interval which would have to be used for a kinetic energy measurement in order to impose a minimum uncertainty of ±1% on the kinetic energy measured. Take the combined mass of cyclist and bicycle to be 100 kg.
Answer T15
From Equation 16b,
Heisenberg uncertainty principle $\Delta E\,\Delta t \gtrsim \hbar$(16b)
$\Delta t \gtrsim \hbar/\Delta E$
In this case
E = Ekin = ½ mυ2 = ½ ×100 kg × 100 m2 s−2 = 5000 J
If ∆E = 2% ∆E = E/50 = 100 J
So$\Delta t = \rm \dfrac{6.63\times10^{-34}\,J\,s}{2\pi\times100\,J} = 1.1\times10^{-36}\,s$
As it is inconceivable that any kind of measurement could be made in this time interval, we find that, as for the answer to Question T13, the Heisenberg uncertainty principle is not relevant in practical terms on a macroscopic scale.
Question T16
An electron occupying a certain energy level in an atom may drop to a lower energy level if it emits a photon with energy corresponding to the difference between the levels.
In a particular case, the average time an electron spends in an excited, high energy level is about 10−8 s. By considering this to be a measure of the time interval during which it may emit the photon, estimate the uncertainty in the photon energy.
What is the fractional uncertainty in the frequency of electromagnetic radiation emitted by such an atom, if the energy difference between the energy levels is 3.0 × 10−19 J?
Answer T16
From Equation 16b,
Heisenberg uncertainty principle $\Delta E\,\Delta t \gtrsim \hbar$(16b)
$\Delta E = \dfrac{\hbar}{\Delta t} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{2\pi\times10^{-8}\,s} = 1.1\times10^{-26}\, J$
From Equation 1,
photon energy E = hf(Eqn 1)
for a photon:
$f = \dfrac Eh\quad\text{so}\quad\dfrac{\Delta f}{f} = \dfrac{\Delta E}{E} = \rm \dfrac{1.1\times10^{-26}\,J}{3.0\times10^{-19}\,J} = 3.7\times10^{-8}$
As such frequency measurements can be made to high accuracy, the width of the measured frequency band can in practice be used to estimate the lifetime of the upper energy level.
5 Applications of quantum theory
Quantum theory is important in providing a detailed understanding of the structure of atoms, but this is dealt with elsewhere in FLAP. Here we will look briefly at one or two other applications which can be understood in terms of the theory covered earlier in this module.
5.1 Diffraction as a probe of crystal structure
The diffraction of electrons by a crystal (i.e. a regular array of atoms) was the experiment which confirmed the electron’s ability to exhibit wave–like behaviour. We can turn this argument around and use an electron beam of known wavelength to study the crystalline structure of a target by observation of the resultant electron diffraction pattern.
As stated in Section 2, the main features of the diffraction pattern depend only on the de Broglie wavelength and not on the kind of particle used. However, different particles may have different interactions with the crystal and different penetrating powers. These differences can be used to probe different aspects of the crystal structure. For example, both X–rays and electrons interact with the electrons of the target atoms but electrons are less penetrating than X–rays and can therefore be used to give more information about surface features. Neutrons, which have no electric charge, interact with the atomic nuclei and are useful for investigating materials with low electron concentrations (for example, materials containing a high proportion of hydrogen atoms).
5.2 Quantum tunnelling
Suppose a marble rolls along a level surface towards a hill, but that the kinetic energy is insufficient for it to reach the top of the hill. Classical physics would predict that the marble would roll some way up the hill, stop, and then roll back down again. In quantum physics, the hill becomes a potential energy barrier that may reflect the wave associated with the particle, but will not necessarily do so. If the barrier is not too high or too thick then, although the wave will be attenuated, it may still have a non–zero amplitude on the far side of the barrier, implying that there is some chance of finding the particle there. If the particle is found in this classically forbidden region we say that it has ‘tunnelled through’ the barrier, and we refer to the whole process as quantum tunnelling. i We would be very surprised indeed if our rolling marble suddenly appeared on the far side of the hill and carried on rolling down the other side! i
From earlier discussions you might suspect that for a macroscopic object, such as a marble on a hill, the quantum prediction is indistinguishable from the classical prediction. This is true and the probability of tunnelling is infinitesimally small in such situations. However, the situation is quite different when we consider subatomic particles; they do not behave in a ‘common sense’ way at all.
A subatomic equivalent of the rolling marble is an electron travelling through a electrical_conductorconductor or semiconductor which is confronted with an insulating gap. For the electron, this constitutes an electrical potential energy barrier in the same way as the hill is a gravitational potential energy barrier for the marble. i Provided we know enough about the nature of the insulator and the size of the gap, we can calculate the size of the barrier. Even when the kinetic energy of the incident electrons is less than the potential energy they must have when within the gap, we find that a certain proportion of electrons penetrate the barrier. The tunnelling probability is very sensitive to the height of the barrier and in appropriate semiconductor materials, this height can be manipulated electronically, allowing the flow of electrons through the barrier (the currenttunnel current) to be switched on and off. A device designed to use this phenomenon to control the current flow in a circuit is called a tunnel diode and these are used widely in electronics to achieve very rapid switching rates, of the order of 109 times per second – so, take care if you are tempted to think that quantum physics has no everyday consequences!
5.3 The size of an atom
Study comment In order to follow the details of Subsection 5.3, you will need to understand simple differentiation and be aware of the formula for electric potential energy of an electron in an atom. However, these details are not essential to meet the achievements for this module.
It is a fundamental law of physics, that any system will move towards the lowest potential energy state available to it. i A simple example is that of a ball on a hill, which will roll down the hill until its gravitational potential energy is at a minimum. Until the arrival of quantum theory, the application of this idea to an electron orbiting around a positively charged nucleus (i.e. the atom) led to the disconcerting result that the lowest potential energy configuration would be reached when the electron collapsed into the nucleus. This implies that atoms should be very unstable – but as many of them have been around for several billion years, this must be incorrect!
Furthermore, all atoms have effective diameters a tenth of a nanometre i or so – but why should they be this size as opposed to any other? Quantum theory, in the shape of the Heisenberg uncertainty principle, provides an answer to both of these puzzles by showing that the most stable configuration for an atom is when it has a diameter of just about a few tenths of a nanometre, rather than when the electron collapses into the nucleus. We will outline this argument briefly.
For simplicity, we will consider a hydrogen atom, as it has a single electron, although the same argument applies in principle to more complicated atoms with many electrons. Now, we can think of the uncertainty in the electron’s position as being roughly equivalent to the atomic diameter a. So, from Equation 14,
$\Delta p_x\,\Delta x \approx \hbar$(Eqn 14a)
the minimum allowable uncertainty in the momentum component in any direction is:
$\Delta p_x \approx \hbar/a$(17)
If we regard the atom as being stationary, the mean electron velocity will be zero (it isn’t going anywhere; it is just staying with the atom) and ∆p can be thought of as the minimum magnitude of momentum that the electron might have at any moment in time. The total energy of the electron in this situation consists of the electric potential energy, Epot, in the electric field of the nucleus, together with the kinetic energy Ekin, due to its motion around the nucleus. The kinetic energy is determined by the magnitude of the momentum, as in Equation 15,
$E = E_{\rm kin} = \dfrac{m\upsilon^2}{2} = \dfrac{(m\upsilon)^2}{2m} = \dfrac{p^2}{2m} = \dfrac{h^2k^2}{8\pi^2m}$(Eqn 15)
and we may take this magnitude p to be given by the minimum magnitude of momentum uncertainty, ∆p, as in Equation 17:
so$E_{\rm kin} = \dfrac{p^2}{2m} = \dfrac{(\Delta p)^2}{2m} = \dfrac{\hbar^2}{2ma^2}$(18)
The potential energy $E_{\rm pot} = -\dfrac{e^2}{2\pi\varepsilon_0a}$(19) i
If we imagine reducing the size of the atom (a becomes smaller) the (positive) kinetic energy increases while the (negative) potential energy decreases. For some value of a there will be a minimum of total energy. We can find this minimum by differentiating the total energy E with respect to a and then setting the result equal to zero. We have:
$E_{\rm tot}= E_{\rm kin} + E_{\rm pot} = \dfrac{\hbar^2}{2ma^2} - \dfrac{e^2}{2\pi\varepsilon_0a}$(20)
The minimum value for Etot occurs when $\dfrac{dE}{da} = 0$, so:
$\dfrac{dE}{da} = -\dfrac{\hbar^2}{ma^3} + \dfrac{e^2}{2\pi\varepsilon_0a^2} = 0$(21) i
i.e.$a = \dfrac{h^2\varepsilon_0}{2e^2\pi m} = \rm \dfrac{(6.63\times10^{-34}\,J\,s)^2\times8.85\times10^{-12}\,C^2\,N^{-1}\,m^{-2}}{2\times(1.60\times10^{-19}\,C)^2\times\pi\times9.11\times10^{-31}\,kg} = 2.65\times10^{-11}\,m$
The measured atomic diameter of hydrogen is 5.29 × 10−11 m. In view of our imprecise use of the uncertainties in the above derivation this agreement is satisfactory. The Heisenberg uncertainty principle has not only explained why atoms are stable, it has also correctly predicted their approximate sizes – a notable achievement for quantum theory!
6 Quantum theory and philosophy
Between 1600 and 1900 the enormous successes of science in explaining natural phenomena led to a certain self–confidence – even arrogance – among scientists about what could be achieved by the application of scientific principles. In particular, it was held by some scientists that the history of the Universe must be predetermined since everything worked according to fixed laws (such as Newton’s laws) in which the state of the Universe at one time entirely determined its state at every later time. Seen from this viewpoint (known as determinism) the Universe operates like an enormous clock. Once set in motion, everything that will happen is pre–ordained because the future development of the Universe can, at least in principle, be calculated exactly. i
The philosophical implications of this are considerable. All biological organisms, including human beings, are made up from atoms. According to a deterministic philosophy, the future of even these atoms is already known from the beginning of time. This is a little uncomfortable for those who believe they have the free will to decide their own destiny.
Quantum theory suggests a rather different picture. First, the initial data on all particles cannot be known in principle because the Heisenberg uncertainty principle tells us we can never have exact simultaneous measurements of position and momentum for any particle. Secondly, even if we had the initial data, we would only be able to predict the probability that any particle would follow a particular path. Some would argue that quantum theory does not return us ‘free will’, it just means that our fates rest on many ‘dice rolls’ which are beyond our control rather than suggesting a totally predetermined future, and so we are still equally powerless to control our future.
Some scientists, including Einstein, have been profoundly unhappy with this idea of a ‘fuzzy’, unknowable Universe. They have argued that quantum theory is an incomplete theory and that the fuzziness is a reflection of our limited understanding and not a feature of the Universe itself. One suggestion is that our current understanding of quantum physics is just a partial comprehension of some deeper hidden variable theory in which everything is completely determined. An analogy can be drawn with our understanding of the behaviour of gases. It was possible for early scientists to devise laws and theories relating to the macroscopic properties of gases such as pressure and volume without any knowledge of why these properties arose. Only later was it shown that the macroscopic theories could be explained in terms of the motions of the molecules which constituted the gas. In the same way, future scientists may make advances which expose precise internal workings of the Universe, so explaining the ‘fuzziness’ which we now see.
However, the advocates of this theory are in a minority. The view of the majority is that the probabilistic nature of quantum theory tells us as much as there is to know. It is not possible, even in principle, to predict the exact path of an individual particle passing through a slit. This view is consistent with the conventional Copenhagen interpretation of quantum theory, as it was formulated by a group of scientists (including Heisenberg) who worked in Copenhagen in the 1920s.
Another alternative interpretation, known as the many Universe interpretation suggests that all possible paths for all particles are actually followed. In our Universe, when we detect a particle which has passed through a slit, we only see the end result of one path, but all the other paths have led to different results in an infinity of other universes. Although this may appear far-fetched, there is nothing in physics to suggest it is wrong and there are some good arguments in its favour. However, most of us have enough trouble with one Universe without worrying about an infinite number of others.
7 Closing items
7.1 Module summary
- 1
-
In the first decade of this century, it was realized that in interactions with matter, electromagnetic radiation can behave like a stream of particles, or photons, with energy E = hf and momentum magnitude p = h/λ. This observation was extended by de Broglie, who suggested that all particles could be associated with waves (now called de Broglie waves). The wavelength of the de Broglie wavelengthde Broglie wave is related to the particle’s momentum magnitude by the expression:
$\lambda_{\rm dB} =\dfrac hp$(Eqn 4)
- 2
-
The de Broglie wave is not a physical wave in the sense that it can be interpreted as an oscillation of a physical quantity; it is simply a means of calculating the probability of finding a particle in a particular region of space from the relationship:
probability ∝ intensity ∝ (amplitude)2(Eqn 11)
- 3
-
The existence of a wave–like aspect to the behaviour of matter has been verified by diffraction experiments on many different kinds of microscopic particles and appears to be present irrespective of the size, mass, charge or composition of the particles. Where there are several paths available to a particle, the associated waves show interference effects. These diffraction and interference effects cannot be explained on the basis of Newton’s laws.
- 4
-
The de Broglie hypothesis suggests that de Broglie waves should also be associated with macroscopic particles, but the predicted effects are too small to be observable at scales much greater than the atomic scale.
- 5
-
One of the consequences of the wave model of matter is that there is a limit on the accuracy with which position and momentum can be measured simultaneously in any given dimension. This is expressed by the Heisenberg uncertainty principle, which in one dimension is written as:
$\Delta x\,\Delta p_x \gtrsim \hbar$(Eqn 14b)
A similar relationship exists for the measurement of energy and the time taken to make the measurement
$\Delta E\,\Delta t \gtrsim \hbar$(Eqn 16b)
- 6
-
Quantum physics has allowed the understanding of the detailed structure of atoms and the development of many technologies, such as structure determination using particle diffraction and section 5.2tunnel effect devices.
- 7
-
Quantum physics argues in principle against a deterministic view of the Universe.
The Copenhagen interpretation holds that the Universe is inherently probabilistic in nature and there is no deeper theory which would allow exact predictions of the behaviour of particles.
7.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Write down the de Broglie relationship between wavelength and momentum for a particle and perform calculations based on this relationship.
- A3
-
Explain how the amplitude of a de Broglie wave relates to the probability of finding a particle in a given region of space and calculate positions of probability maxima and minima for particles diffracted through parallel slits of known size.
- A4
-
Write down the Heisenberg uncertainty principle for position and momentum and describe (without proof) how it can be derived from simple wave theory and perform simple calculations based on it.
- A5
-
Write down the Heisenberg uncertainty principle for energy and time and perform simple calculations based on it.
- A6
-
Describe (without proof) how the uncertainty relation can be used to give an approximate value for the expected size of a hydrogen atom.
- A7
-
Explain why quantum physics is very important in terms of modelling the Universe at an atomic scale but can generally be ignored at a macroscopic scale.
- A8
-
Explain what is meant by the Copenhagen interpretation of quantum theory and indicate one philosophical implication of this interpretation.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
7.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
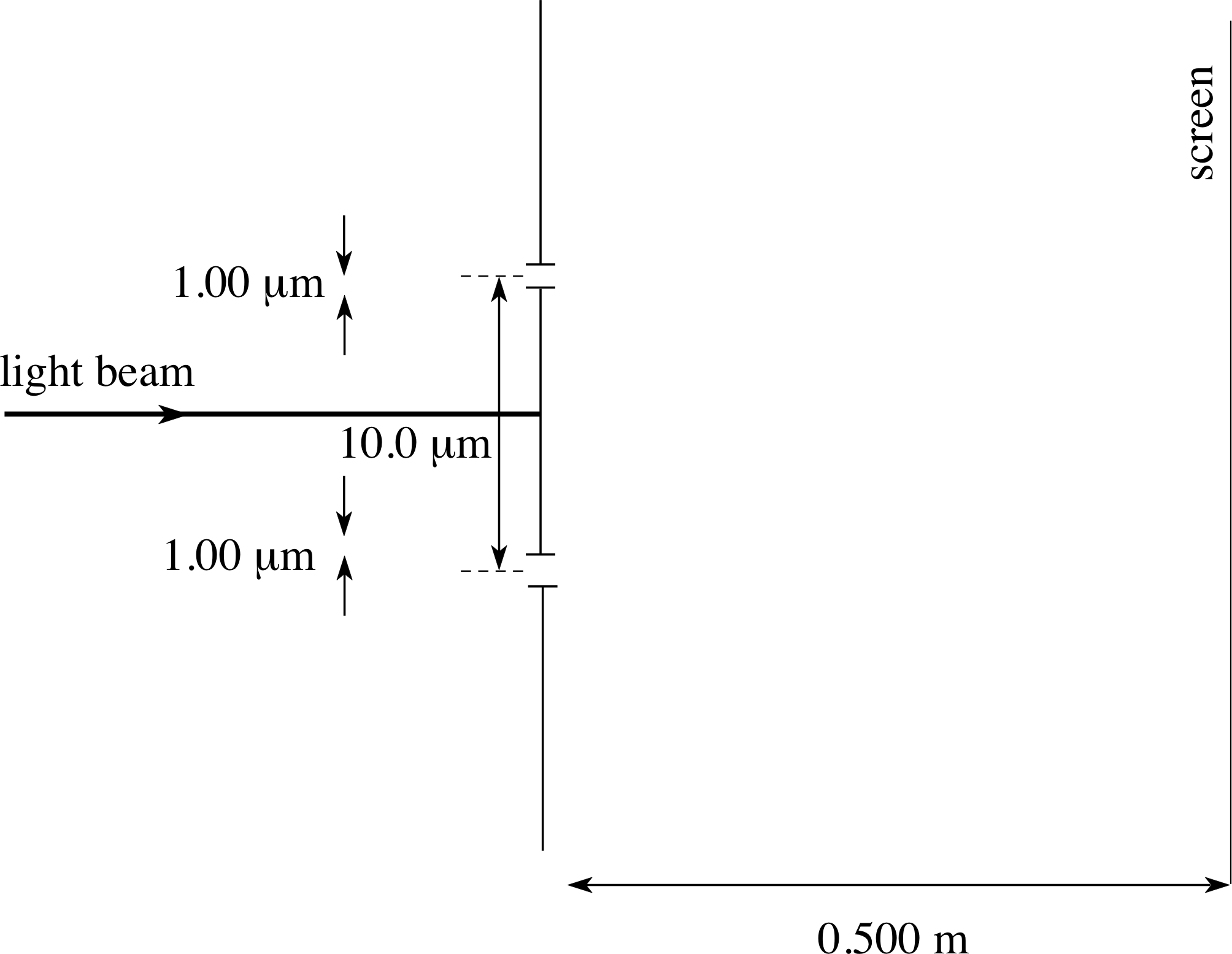
Figure 10 See Question E1.
Question E1 (A2, A3 and A7)
A parallel light beam of wavelength 0.500 μm is directed at a pair of very narrow slits in an opaque barrier positioned perpendicular to the beam direction. The width of each slit is 1.00 μm and the slit separation 10.0 μm. The diffracted beam is detected by a light–sensitive screen at a distance of 0.500 m beyond the barrier, perpendicular to the initial beam direction. The screen is sufficiently sensitive to register the arrival of individual photons. The arrangement is shown schematically in Figure 10.
(a) Calculate the momentum of an individual photon.
(b) Sketch a graph on Figure 10, showing the variation of intensity with position along the screen. Indicate clearly the positions of maxima and minima.
(c) Say whether it is possible to calculate the position on the screen at which the first photon arrives after the beam is switched on. If you think it is possible, calculate where it will arrive.
If you think it is not possible, can you make any statement at all about where the photon is likely to go.
(d) Describe how the arrival pattern will change if one slit is covered.
(e) Explain why the same patterns of maxima and minima would not be achieved with a machine gun firing bullets through two slits in an armour plated wall.
Answer E1

Figure 6 The diffraction patterns for the situations described in Questions T7 to T9. The dashed line is for slit A open; the solid line is for slit B only open and the dotted line is for both slits open. (The intensity units in this figure are arbitrary.)
(a)
$p = \dfrac{h}{\lambda} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{5.00\times10^{-7}\,m} = 1.33\times10^{-27}\,kg\,m\,s^{-1}$
(b) The diffraction pattern on the screen would show the intensity variation with position as plotted by the dotted line in Figure 6, with maxima given (as in the answer to Question T2) by
$x = \dfrac{n\lambda L}{\sqrt{d^2-n^2\lambda^2}}$
For n = 1:
$x = \rm \dfrac{1\times5.00\times10^{-7}\,m\times0.500\, m}{\sqrt{\smash[b]{(1.00\times10^{-5}\,m)^2 - 1\times(5.00\times10^{-7}\,m)^2}}}\\ \phantom{x }= 2.50\times10^{-2}\,m$
Similarly:
For n = 2 x = 5.03 × 10−2 m
For n = 3 x = 7.59 × 10−2 m
(c) It is not possible to predict the point of arrival on the screen of the first photon or any other photon. It is possible, however, to estimate the probability of arrival of a particular photon at a particular point as this is proportional to the wave intensity at the screen. In particular, it is possible to say that it will definitely not arrive at any point where the intensity is calculated to be zero.
(d) If one slit is closed then the arrival pattern on the screen will change into a single slit diffraction pattern, with a central broad maximum, centred around the line through the single slit, and with narrower subsidiary maxima on each side of the central one, as in the dashed and solid lines of Figure 6.
(e) Bullets fired from a gun would have momenta of the order of tens or hundreds of kg m s−1. From Equation 4,
$\lambda_{\rm dB} =\dfrac hp$(Eqn 4)
this would give de Broglie wavelengths of around 10−32 m or 10−33 m. As the first diffraction maximum occurs for sin θ1 = λdB/d, then any realistic size for d would give values for θ1 which would be much too small to measure.
(Reread Subsection 3.3 and Answer T10 if you had difficulty with this question.)
Question E2 (A4)
Fourier analysis shows that, for all wave motions, a wavetrain of length ∆x can be constructed by adding together a number of infinite wavetrains over a range ∆kx such that ∆x ∆kx ≈ 1. Use this result to derive the Heisenberg uncertainty principle in one dimension.
Answer E2
From Equation 7,
$k = \dfrac{2\pi}{\lambda}$(Eqn 7)
and the de Broglie’s equation,
$k = \dfrac{2\pi}{\lambda} = \dfrac{2\pi p}{h} = \dfrac{p}{\hbar}$
$\Delta k_x= \dfrac{\Delta p_x}{\hbar}\quad\text{and}\quad\Delta x\,\Delta k_x \approx (1/\hbar)\Delta x\,\Delta p_x \approx 1$
Using Equation 12,
∆x ∆k ≈ 1(Eqn 12)
It then follows that: $ \Delta x\,\Delta p_x \approx \hbar$
(Reread Subsections 2.2, 2.3 and 4.1 if you had difficulty with this question.)
Question E3 (A4 and A6)
Probably the simplest model of an electron in a hydrogen atom is to consider it as a particle of mass 10−30 kg confined to a region 10−10 m. By considering this situation in one dimension, use the Heisenberg uncertainty principle to derive an order of magnitude estimate for the kinetic energy of the electron in the hydrogen atom.
Answer E3
The electron’s velocity averaged over a long enough time interval is zero relative to the nucleus, so the uncertainty in its momentum in any direction can be regarded as a rough estimate of its likely momentum in that direction at any particular moment
$p \approx \Delta p \approx \dfrac{\hbar}{\Delta x} = \rm \dfrac{6.63\times10^{-34}\,J\,s}{2\pi\times 10^{-10}\,m} \approx 1.1\times10^{-24}\,kg\,m\,s^{-1}$
The kinetic energy is Ekin = p2/2m, so taking ∆p as an estimate of p we have:
$E_{\rm kin} = \dfrac{p^2}{2m} \approx \rm \dfrac{(1.1\times10^{-24}\,kg\,m\,s^{-1})^2}{2\times10^{-30}\,kg} = 6.1\times10^{-19}\,J$
This model is an extremely crude attempt at a hydrogen atom. It has ignored the three–dimensional nature of the atom and has ignored all potential energy. Nevertheless, it has predicted the kinetic energy of the electron in the ground state of atomic hydrogen to within a factor of four (actually the measured value of kinetic energy is about 22 × 10−19 J).
(Reread Subsections 4.1 and 4.2 if you had difficulty with this question.)
Question E4 (A6)
In the atoms of a certain element, electrons can be excited to a high energy level where they remain for a short time before dropping down to a lower energy level with a long lifetime. When an electron drops to the lower level, it emits a photon. A detector, designed to register photons corresponding to this transition, records a range of frequencies ∆f = 2.0 × 108 Hz. Estimate the average lifetime of an electron in the high energy state.
Answer E4
From Equation 1:
photon energy E = hf(Eqn 1)
∆E = h∆f
Substituting this into Equation 16b,
Heisenberg uncertainty principle $\Delta E\,\Delta t \gtrsim \hbar$(Eqn 16b)
gives us:
$h\Delta f\,\Delta t \gtrsim \hbar$
or, the lifetime $\Delta t \gtrsim \dfrac{1}{2\pi\Delta f} = \rm \dfrac{1}{2\pi\times2.0\times10^8\,s^{-1}} = 8.0\times10^{-10}\,s$
(Reread Subsection 4.4 if you had difficulty with this question.)
Question E5 (A8)
Explain briefly why most physicists no longer hold a deterministic view of the Universe.
Answer E5
A deterministic view of the Universe suggests that if the exact positions and momenta of all particles are known and if all particles operate according to the laws of classical physics, it is possible, in principle, to predict the future path of every particle for all time. Hence the future of the Universe and everything in it is predetermined.
The Copenhagen interpretation of quantum theory argues against this in two ways. First, the Heisenberg uncertainty principle states that it is inherently impossible to know simultaneously the exact position and momentum of any particle. Secondly, even if we could have the initial data on a particle with perfect accuracy, we can only predict the probability of that particle following a particular path in the future. According to the Copenhagen interpretation, this ‘unknowability’ is a feature of the way the Universe works and not simply a reflection of our imperfect understanding. From this viewpoint, the Universe is definitely not deterministic.
(Reread Section 6 if you had difficulty with this question.)
Question E6 (A7)
A cyclist is freewheeling along a level road towards a hill. The speed of the cyclist is such that she has insufficient kinetic energy to reach the top of the hill without pedalling. Suddenly, she finds herself on the other side of the hill. Explain why this might be a possible, if unlikely, occurrence.
Answer E6
A de Broglie wave interpretation of the cyclist freewheeling towards the hill is of a wave travelling towards a potential barrier. The wave will be partially reflected from the barrier (giving a probability that the bicycle will come to a stop and roll back down) and partially transmitted through it (giving a probability that the cyclist will appear on the other side). On a subatomic scale, for example, electrons in a conductor reaching an insulating gap, the probability of their appearing on the other side of the barrier is significant; for a macroscopic object such as the cyclist, the probability of tunnelling through the barrier is unimaginably small.
(Reread Subsection 4.3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 7Closing items.