MATH 4.2: Basic differentiation |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Being able to differentiate accurately and confidently is a necessary skill for any physicist. Differentiation is such a powerful tool with so many applications that it is worth some effort to ensure that you have mastered the techniques explained in this module.
The main objective of this module is to answer the following question:
‘If we know how to differentiate two functions f (x) and g (x), how do we differentiate their sum, difference, product and quotient?’
To answer this question we discuss first the idea of a function and how functions can be combined to produce new ones. Section 2 examines the mathematical basis of differentiation, giving first a graphical interpretation and then a formal definition.
Section 3 answers our question and is the core of the module. It provides a list of derivatives of various standard functions (such as power functions (xn) and trigonometric functions) and introduces the various rules that will enable you to differentiate a wide range of combinations of these standard functions. In particular it will explain how to differentiate sums, constant multiples, products and quotients of the standard functions. Sometimes the method is straightforward, as with the derivative of a sum, but it may also be quite complicated, as with the derivative of a quotient.
We also discuss the logarithmic and exponential functions, and, while loge x and ex are the most important of such functions, it is sometimes necessary to be able to differentiate loga x and ax where a is some positive number other than e. In Section 4 we consider why ex is so important and then add ax and loga x to the list of functions that can be differentiated.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Differentiate each of the following functions (it is not necessary to simplify your answers).
(a) f (x) = x2 sin x + loge x
(b) f (x) = (x3 − 6x)(2x2 + 5x − 1) (use the product rule)
(c) $f(x) = \dfrac{1}{\sin x}$
(d) $f(x) = \dfrac{x^2+}4x-1{x^+9}$
(e) $f(x) = \dfrac{x\tan x}{3x^2-2x+1}$
(f) f (x) = x2 − 2x + 1
(g) f (x) = (ex + e−x)2
Answer F1
(a) f ′ (x) = x2 cos x + 2x sin x + (1/x).
(b) f ′ (x) = (x3 − 6x)(4x + 5) + (3x2 − 6)(2x2 + 5x − 1) = 10x4 + 20x3 − 39x2 − 60x + 6.
(c) f (x) = 1/sin x = cosec x, so f ′ (x) = −cosec x cot x.
(d) $f'(x) = \dfrac{(2x + 4)(x^2 + 9) - (x^2 + 4x - 1)2x}{(x^2+9)^2}$
(e) $f'(x) = \dfrac{(x\sec^2x + \tan x)(3x^2-2x + 1) - x\tan x(6x - 2)}{(3x^2-2x+1)^2}$
(f) f ′ (x) = (loge 2) 2x + 2x Note that e2 is a constant.
(g) f (x) = (ex + e−x)(ex + e−x), so using the product rule we find
f ′ (x) = (ex + e−x)(ex + e−x) + (ex + e−x)(ex + e−x) = 2 (ex + e−x)
Question F2
If at time t the displacement, sx(t), of a particle along the x–axis from some particular reference point is given by
sx(t) = e−αt [A cos(ωt) + B sin(ωt)]
where A, B, α and ω are constants, find expressions for vx(t), the velocity at time t, and ax(t) the acceleration at time t, and show that
ax(t) + 2αvx(t) + (ω2 + α2)sx(t) = 0
Answer F2
sx(t) = exp(−αt)[A cos(ωt) + Bsin(ωt)]
vx(t) = $\dfrac{d}{dt}$sx(t) = exp(−αt)[−Aω sin(ωt) + Bω cos(ωt)] − α exp(−αt)[A cos(ωt) + B sin(ωt)]
Sovx(t) = ω exp(−αt)[−Asin(ωt) + B cos(ωt)] − αsx(t)
ax(t) = vx′ (t) = ω2 exp(−αt)[−A cos(ωt) − B sin(ωt)] − αω exp(−αt)[−Asin(ωt) + B cos(ωt)] − αvx(t)
Soax(t) = −ω2sx(t) −αω exp(−αt)[−A sin(ωt) + B cos(ωt)] − αvx(t) = −ω2sx(t) − αvx(t) − α2sx(t) − αvx(t)
using the expression for vx(t), and therefore
ax(t) + 2αvx(t) + (ω2 + α2)sx(t) = 0
1.3 Ready to study?
Study comment To begin the study of this module you will need to be familiar with the following terms: base_of_a_logarithmbase (of a logarithm_to_base_elogarithm), exponential function, inequality (in particular inequalitygreater than (>) and inequalityless than (<)), integer, inverse function, logarithmic function, modulus (or absolute value, | x |), product, quotient, radian, real number, reciprocal, set, square root, sum, trigonometric function and trigonometric identities. (The trigonometric identities that you require are repeated in this module, as is the definition of the modulus function.) In addition you will need to have some familiarity with the concept of a function, and with related terms such as argument, codomain, domain and variable (both dependent and independent), but the precise meaning of these terms is briefly reviewed in the module. Similar comments apply to physics concepts used in this module, such as acceleration, displacement, force, speed, velocity and Newton’s second law. If you are uncertain of any of these items you can review them now by referring to the Glossary, which will indicate where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics, or to improve your general algebraic skills, before embarking on this module.
Question R1
Write the following sums, products and quotients of logarithms and exponentials as compactly as you can:
(a) log10 x + log10 y, (b) (log2 14 × log2 14)3, (c) loge x − loge y, (d) ex/ey, (e) (ex/ey)2, (f) loge x + loge x + loge x.
Answer R1
(a) log10xy, (b) (2 × 2)3 = 64, (c) loge(x/y), (d) ex−y, (e) e2x−2y, (f) 3 loge x = loge x3.
Consult logarithm_to_base_10logarithm and exponential_functionexponential in the Glossary for further details.
Question R2
If f (x) = cos x, g (x) = sin x, and h (x) = tan x, rewrite the following expressions in terms of trigonometric functions and simplify them where possible i :
(a) [f (x) + g (x)]2
(b) f (x)h (x) + g (x)/h (x)
(c) [f (x) − g (x)]/[1 + h (x)]
Answer R2
(a) [f (x) + g (x)]2 = (cos x + sin x)2 = cos2x + 2 cos x sin x + sin2 x
Since sin2 x + cos2 x = 1 and sin(2x) = 2 sin x cos x, for all x, we can write
[f (x) + g (x)]2 = 1 + sin(2x).
(b) f (x)h (x) + g (x)/h (x) = cos x tan x + sin x/tan x = $\cos x \times \dfrac{\sin x}{\cos x} + \sin x \times \dfrac{\cos x}{\sin x} = \sin x + \cos x$
(c) $\dfrac{f(x)-g(x)}{1+h(x)} = \dfrac{\cos x-\sin x}{1 + \tan x}$
which cannot be simplified.
Consult trigonometric functions and trigonometric identities in the Glossary for further details.
Question R3
Given that $f(x) = \dfrac{x^2}{4}-1$, find the following values: f (1), f (0), f (−2), | f (0) |, | f (0) − f (−2) | and sketch the graph of y = f (x)
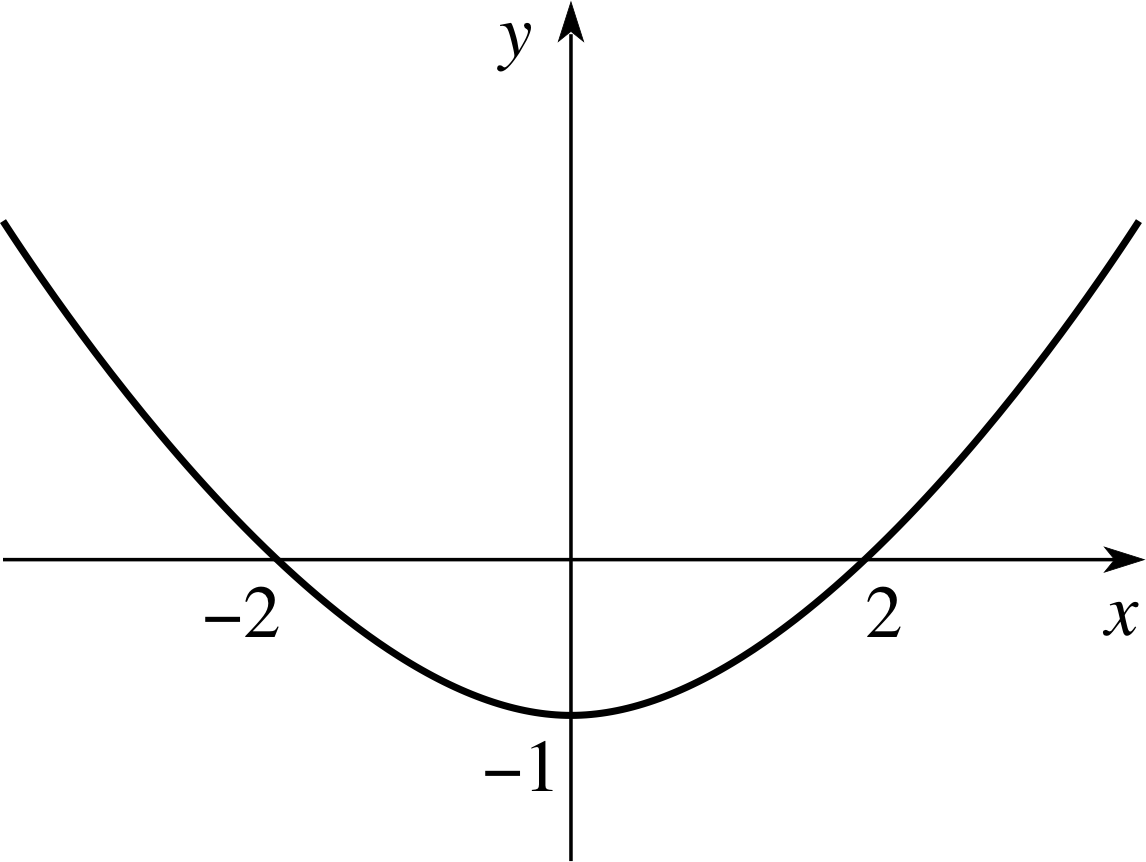
Figure 7 See Answer R3.
Answer R3
f (1) = −0.75, f (0) = −1, f (−2) = 0, | f (0) | = 1, | f (0) − f (−2) | = 1.
The graph of $y=\dfrac{x^2}{4}-1$ is shown in Figure 7.
Consult functions and modulus in the Glossary for further details.
Question R4
Given that ax and loga x are inverse functions, simplify the following i :
(a) loge[e2 log10(x)], (b) exp(loge(10x)), (c) log2(22).
Answer R4
(a) 2 log10 x, (b) 10x, (c) 2.
Consult inverse functions in the Glossary for further details.
2 Variables, functions and derivatives
2.1 Functions and variables
Study comment An understanding of functions is crucial to an understanding of differentiation, and it is vital that the notation and terminology used to describe functions should be clear and unambiguous. For that reason, this subsection reviews the definitions of terms such as function and variable even though it is assumed that you have met these ideas before. If you are completely unfamiliar with these concepts you should consult the entry on functions in the Glossary.
A function f is a rule that assigns a single value f (x) in a set called the codomain to each value x in a set called the domain.
Functions are very often defined by formulae, for example f (x) = x2, and in such cases we assume, unless we are told otherwise, that the domain is the largest set of real values for which the formula makes sense. In the case of f (x) = x2 the domain of the function is the set of all real numbers. The function $g(x) = \dfrac{1}{1-x}$ is not defined when x = 1, since 1/0 has no meaning, and so we take the set of all real numbers x with x ≠ 1 as its domain.
The function
f (x) = 1 + x + x2(1a)
is another example of a function that is defined for all values of x.
One may think of the function as a sort of ‘machine’ with x as the input and 1 + x + x2 as the output. The input x is known as the independent variable and, if we write y = f (x), the output y is known as the dependent variable since the function f (x) determines the way in which y depends on x.
It is important to note that the same function f could equally well be defined using some other symbol, such as t, to represent the independent variable:
f (t) = 1 + t + t2(1b)
This freedom to relabel the independent variable is often of great use, though it is vital that such changes are made consistently throughout an equation. We may calculationevaluate the function in Equation 1, whether we call it f (x) or f (t), for any value of the independent variable; for example, if we choose to use x to denote the independent variable, and set x = 1, we have
f (1) = 1 + 1 + 12 = 3
Similarly, if x = π f (π) = 1 + π + π2
and, if x = 2a f (2a) = 1 + (2a) + (2a)2 = 1 + 2a + 4a2
We may even apply the function to 2x, −x, or 1 + x to obtain
f (2x) = 1 + (2x) + (2x)2 = 1 + 2x + 4x2
f (−x) = 1 + (−x) + (−x)2 = 1 − x + x2
f (1 + x) = 1 + (1 + x) + (1 + x)2 = 3 + 3x + x2
When we write expressions such as f (π) or f (2a), whatever appears within the brackets is called the argument of the function. The value of f (x) is determined by the value of its argument, irrespective of what we call the argument.
A special note about $\boldsymbol{\sqrt{x\os}}$: Generally in FLAP we follow the convention that $\sqrt{x\os}$ may be positive or negative. Thus $\sqrt{4\os} = \pm 4$. A consequence of this convention is that $f(x) = \sqrt{x\os}$ does not define a function since it does not associate a unique value of f (x) with each value of x. This would be an exceptionally inconvenient convention to follow in this module so instead we adopt the convention that $\sqrt{x\os}$ is positive. Of course, it remains true that the square roots of $\sqrt{x\os}$ may be positive or negative, $\sqrt{x\os}$ or $-\sqrt{x\os}$, so within this convention we should call $\sqrt{x\os}$ the positive square root o f$\sqrt{x\os}$, and not simply the square root. In a similar spirit $x^{1/2} = \sqrt{x\os}$ will also be a positive quantity.
✦ If f (x) = cos2 x + sin x find f (2x) and $f\left(\dfrac{\pi}{4}\right)$ i
✧ f (2x) = cos2 2x + sin 2x
and
$f\left(\dfrac{\pi}{4}\right) = \cos^2\dfrac{\pi}{4} + \sin\dfrac{\pi}{4} = \left(\dfrac{1}{\sqrt{2\os}}\right)^2+\dfrac{1}{\sqrt{2\os}} = \dfrac12+\dfrac{\sqrt{2\os}}{2} = \dfrac{1+\sqrt{2\os}}{2}$ i
Question T1
If f (x) = x2 + 1 and g (x) = 2x,
(a) Write down expressions for $f\left(\sqrt{x\os}\right)$ and $g\left(\dfrac x2\right)$.
(b) For which values of the independent variable x is f (x) = g (x)?
(c) For which value of the independent variable x is the following true?
$\dfrac{f(x + 0.1) - f(x)}{0.1} = 0.2$
Answer T1
(a) f ( x ) = ( x )2 + 1 = x + 1, and g (x/2) = 2 (x/2) = x.
(b) We need x2 + 1 = 2x, i.e. x2 − 2x + 1 = 0. The solution of this is x = 1.
(c) f (x + 0.1) − f (x) = (x + 0.1)2 + 1 − (x2 + 1) = x2 + 0.2x + 0.01 + 1 − x2 − 1 = 0.2x + 0.01
So,$\dfrac{f(x+0.1)-f(x)}{0.1} = \dfrac{0.2x+0.01}{0.1} = 2x+0.1$
If this equals 0.2 we must have 2x = 0.1, which gives x = 0.05.
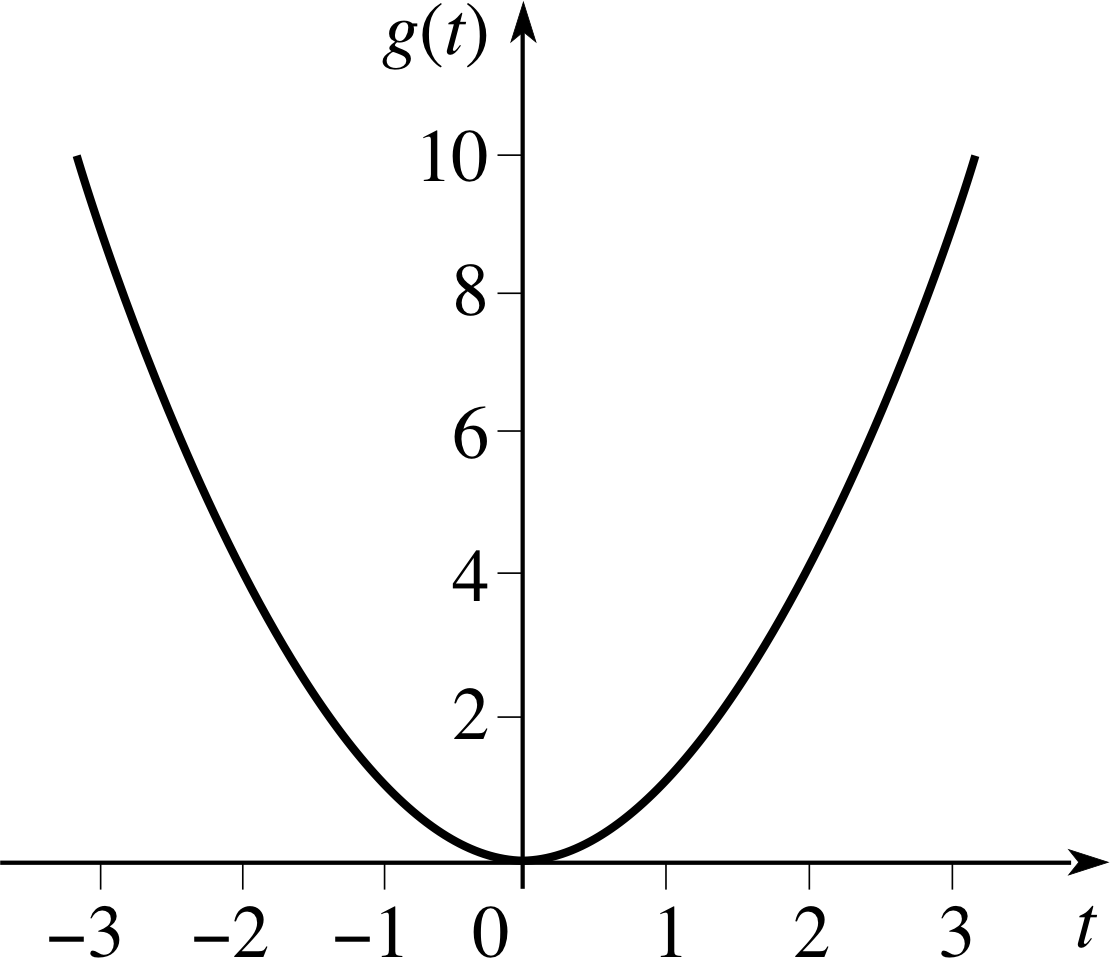
Figure 1 The graph of g (t) = t2.
2.2 Rates of change, gradients and derivatives
The graph of the function g (t) = t2 is shown in Figure 1. It is clear from the graph that as the value of t increases from t = 0, the value of g (t) also increases from 0. In particular, note that as t increases from 0 to 1 the value of g (t) changes from 0 to 1, and that as t increases from 1 to 2 the value of g (t) changes from 1 to 4. Thus, the change in the value of g (t) that corresponds to a change of one unit in the value of t depends on the initial value of t. For this particular function, if the initial value of t is large, then the change in g (t) will also be large; for example, the change in g (t) from t = 100 to t = 101 is
g (101) − g (100) = 1012 − 1002 = 201
Clearly, as t increases the rate at which g (t) is changing is itself changing, becoming greater and greater. How are we to measure the rate at which a function changes? If you imagine yourself walking up a hill in the shape of the graph shown in Figure 1, starting at t = 0 and travelling to the right, your path would become steeper and steeper. It would become increasingly difficult to make progress, because, with each step you took, the slope would become greater and your walk would become more and more of a climb. The slope of the graph is the key; once we can describe the slope precisely for any value of t, we will be able to measure the rate of change of the function g (t) – or of any other function.
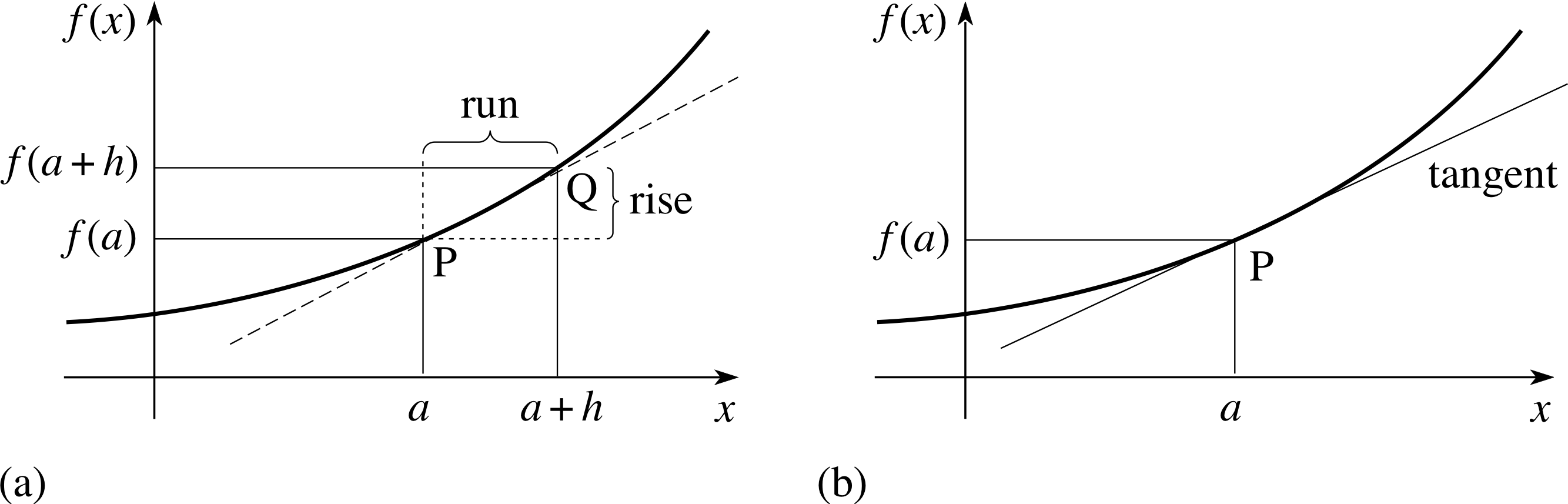
Figure 2 The graph of an arbitrary function.
The graph of an arbitrary function f (x) is shown in Figure 2a. Roughly speaking, the slope of this graph at the point P, where x = a and f (x) = f (a), is the same as the slope of the dashed straight line PQ where Q is a nearby point corresponding to x = a + h and f (x) = f (a + h). Of course, the two slopes are not exactly the same; the point P is fixed and its location determines the slope of f (x) at P, whereas the slope of the line PQ will depend on the location of Q as well as that of P. Nonetheless, the two slopes are similar, so we can roughly describe the slope of the curve in terms of the gradient of the line PQ which is defined by
$\text{gradient of the line PQ} = \dfrac{\text{rise}}{\text{run}} = \dfrac{f(a + h) - f(a)}{(a + h) - a} = \dfrac{f(a + h) - f(a)}{h}$(2) i
Now, the line PQ (the dashed line in Figure 2a) that cuts the graph of f (x) at P and Q and is called a chord, but if we let the point Q get closer and closer to P then this chord becomes more and more like the tangent_to_a_curvetangent in Figure 2b that just touches the graph at P. It is the gradient of this tangent that really represents the slope of the curve at P, this is clear from the figure and from the fact that the gradient of the tangent (unlike that of the chord) is determined by the location of P alone. Fortunately, the gradient of the tangent is fairly easy to work out, all we have to do is to consider what happens to the gradient of the chord PQ as Q gets closer and closer to P. As Q approaches P, h gets smaller and the gradient of the chord PQ approaches the gradient of the tangent at P ever more closely.
Expressed more formally, the gradient of the tangent at P is given by Equation 2 in the limit as h tends to zero.
$\displaystyle \text{gradient of tangent at P} = \lim_{h\rightarrow 0}\left[\dfrac{f(a + h) - f(a)}{h}\right]$(3)
Since this gradient represents the slope of the graph of f (x) at P, it makes sense to define the gradient of the graph of f (x) at P to be the gradient of its tangent at P. We call this gradient the derivative of f (x) at x = a and denote it by f ′ (a) so that
$\displaystyle f'(a) = \lim_{h\rightarrow 0}\left[\dfrac{f(a + h) - f(a)}{h}\right]$(4)
The derivative at x = a defined in this way also represents the rate of change of f (x) with respect to x when x = a. This last point is even easier to appreciate if we introduce a dependent variable y such that y = f (x), for we can the represent the vertical rise in Figure 2a by ∆y = f (a + h) − f (a), and the horizontal run by ∆x = h. With these definitions it follows from Equation 4 that the derivative at x = a is given by
$\displaystyle f'(a) = \lim_{h\rightarrow 0}\left(\dfrac{\Delta y}{\Delta x}\right)$
Even greater emphasis can be given to the idea that the derivative is a rate of change with respect to x by replacing f ′ (a) by the alternative symbol $\dfrac{dy}{dx}(a)$. i
Thus,$\displaystyle \dfrac{dy}{dx}(a) = f'(a) = \lim_{h\rightarrow 0}\left(\dfrac{\Delta y}{\Delta x}\right)$(5)
The definition of the derivative at x = a represented by Equations 4 and 5 can be applied at any point on the graph provided that ∆y and ∆x can be defined at that point and their quotient ∆y/∆x has a unique limit as ∆x → 0 at that point. Thus, provided the derivative of f (x) exists at every point within some domain (i.e. some set of x values) it is possible to define a new function on that domain that associates any given value of x with the gradient of f (x) at that point. This new function is called the derived function or derivative of f (x) and is written f ′ (x) or $\dfrac{df}{dx}(x)$. If y = f (x), the derived function may also be written $\dfrac{dy}{dx}(x)$ or just $\dfrac{dy}{dx}$. i Thus, provided unique limits exist:
$\displaystyle \dfrac{dy}{dx} = \lim_{h\rightarrow 0}\left[\dfrac{f(a + h) - f(a)}{h}\right]$(6)
When using this formula it is important to remember that dy/dx is not a quotient of two quantities dy and dx even though it may look like one. At a given value of x, the derivative dy/dx represents the gradient of the graph of y = f (x) at that value of x.
Although the graphical interpretation of the derivative is important, it does not lend itself to calculation since drawing tangents can only be approximate, and in any case it would be impossible to do it for every point on the graph. However, in simple cases it is not difficult to determine the derivative from the formula for the function and the above definition (Equation 6). Consider the case of f (x) = x2, for which
$\displaystyle f'(x) = \lim_{h\rightarrow 0}\left[\dfrac{f(a + h) - f(a)}{h}\right] = \lim_{h\rightarrow 0}\left[\dfrac{(x + h)^2 - x^2}{h}\right] = \lim_{h\rightarrow 0}\left(\dfrac{2xh+h^2}{h}\right)$
i.e.$\displaystyle f'(x) = \lim_{h\rightarrow 0}\,(2+h) = 2x$
so that f ′ (x) = 2x
The function f (x) = x2 has the set of all real numbers as its domain, and its derivative f ′ (x) = 2x has the same domain.
As a further example, we can use the definition to obtain the derivative of the function f (x) = 1/x.
In this case $f(x) = \dfrac{1}{x+h}$
giving us
$\dfrac{f(x+h)-f(x)}{h} = \dfrac1h\left(\dfrac{1}{x+h}-\dfrac1x\right) = \dfrac1h\left(\dfrac{x-(x+h)}{(x+h)x}\right) = \dfrac{-1}{(x+h)x}$
As h tends to zero the expression $\dfrac{-1}{(x+h)x}$ approaches $-\dfrac{1}{x^2}$
So,$\displaystyle f'(x) = \lim_{h\rightarrow 0}\left[\dfrac{-1}{(x+h)x}\right] = -\dfrac{1}{x^2}$(7)
The function f (x) = 1/x has the set of all non–zero real numbers as its domain, and its derivative f ′ (x) = −1/x2 has the same domain.
Question T2
(a) If f (x) = 1/(ωx) where ω is a constant, use the definition of the derivative to find f ′ (x).
(b) If g (t) = 1/(ωt) use the answer to part (a) to write g ′ (t) and g ′ (2t).
Answer T2
(a) $\dfrac{f(x+h)-f(x)}{h} = \dfrac1h\left[\dfrac{1}{\omega(x+h)}-\dfrac{1}{\omega x}\right] = \dfrac{1}{\omega}\times\dfrac1h\left(\dfrac{1}{x+h}-\dfrac1x\right)$
which is 1/ω times the expression discussed earlier in this subsection, and so
$f'(x) = \dfrac{1}{\omega}\left(-\dfrac{1}{x^2}\right) = -\dfrac{1}{\omega x^2}$
(b) g is the same function as f and therefore
$g'(x) = \dfrac{1}{\omega t^2}$ and $g'(2t) = -\dfrac{1}{\omega(2t)^2} = -\dfrac{1}{4\omega t^2}$
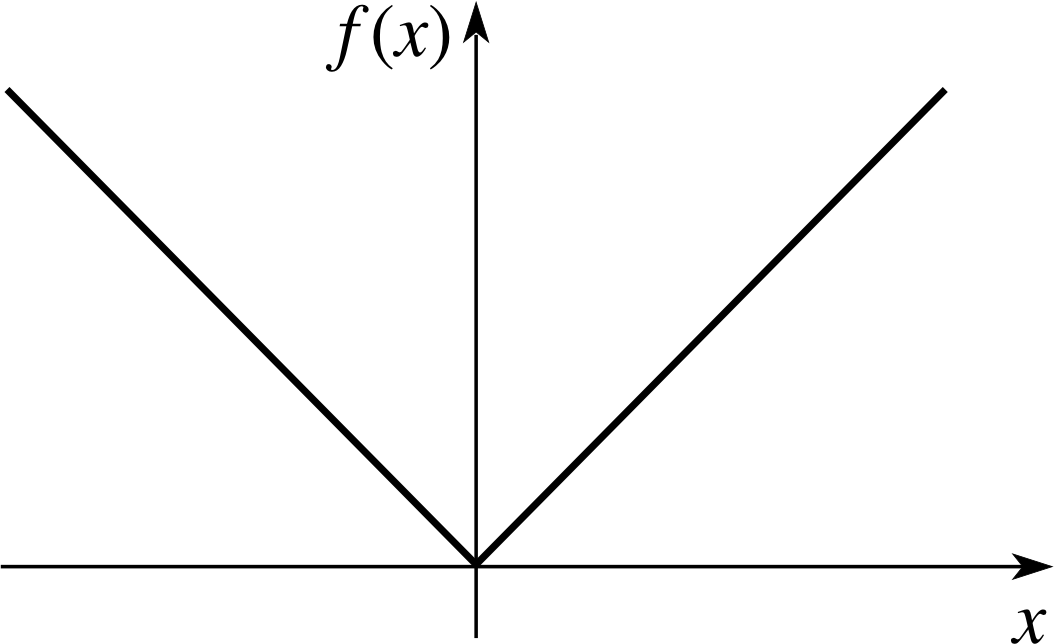
Figure 3 The graph of f (x) = | x |.
Don’t be misled into thinking that if a function exists then its derivative must also exist. The function f (x) = | x | (‘the modulus of x’) illustrates the situation where the derivative has a smaller domain than the function (see Figure 3). The modulus of x is defined by
| x | = x if x > 0
and| x | = −x if x < 0
For positive x the graph of f (x) = | x | is a straight line with gradient 1, so
f ′ (x) = 1 if x > 0
while for negative x the graph is a straight line with gradient −1, so
f ′ (x) = −1 if x < 0
However, when x = 0 no unique limit exists since we get different values for the limit depending on how we calculate it. In particular, if we approach x = 0 from the positive side, where x > 0 and h is positive
$\displaystyle \lim_{h\rightarrow 0+}\left[\dfrac{f(0 + h) - f(0)}{h}\right] = \lim_{h\rightarrow 0+}\left(\dfrac{(\vert\,h\,\vert-\vert\,0\,\vert)}{h}\right) = \lim_{h\rightarrow 0+}\left(\dfrac{(\vert\,h\,\vert}{h}\right) = 1$
whereas, if we approach x = 0 from the negative side, where x < 0 and h is negative
$\displaystyle \lim_{h\rightarrow 0-}\left[\dfrac{f(0 + h) - f(0)}{h}\right] = \lim_{h\rightarrow 0-}\left(\dfrac{(\vert\,h\,\vert-\vert\,0\,\vert)}{h}\right) = \lim_{h\rightarrow 0-}\left(\dfrac{(\vert\,h\,\vert}{h}\right) = -1$
So, if h approaches zero through positive values the limit is 1, but if h approaches zero through negative values the limit is −1. A unique limit exists only if we obtain the same result no matter how h approaches 0. Since different answers have been obtained in this case there is no unique limit and hence no derivative at x = 0. Although the original function is defined for all real values of x the derivative is only defined for non–zero values of x.
On the whole, the domains of functions are of more concern to mathematicians than to physicists. Nonetheless, it is important that you should be aware of their significance, and prepared to investigate them if necessary.
Question T3
(a) Use your calculator to convince yourself that $\dfrac{{\rm exp}(h) - 1}{h}$ i is very nearly equal to 1 when h is very small.
(b) Let f (x) = exp(x). What does part (a) tell you about f ′ (0)?
(c) Use the fact that $\displaystyle \lim_{h\rightarrow 0}\left[\dfrac{{\rm exp}(h) - 1}{h}\right] = 1$, and the definition of the derivative to show that f ′ (x) = exp(x).
Answer T3
(a) Trying various small values (either positive or negative) for h, you should have convinced yourself that
$\displaystyle \lim_{h\rightarrow 0}\left[\dfrac{{\rm exp}(h)-1}{h}\right] = 1$, for example $\dfrac{{\rm exp}(0.001)-{\rm exp}(0)}{0.001} = \dfrac{1.001\,000\,500\,17 - 1}{0.001} = 1.000\,500\,17$
(b) Part (a) should have convinced you that
$\displaystyle f'(0) = \lim_{h\rightarrow 0}\left[\dfrac{{\rm exp}(h)-1}{h}\right] = \lim_{h\rightarrow 0}\left[\dfrac{{\rm exp}(h)-1}{h}\right] = 1$
(c) Keeping in mind the result of part (b)
$\displaystyle f'(x) = \lim_{h\rightarrow 0}\left[\dfrac{{\rm exp}(x+h)-{\rm exp}(x)}{h}\right] = \lim_{h\rightarrow 0}\left[\dfrac{{\rm exp}(x)\,{\rm exp}(h)-{\rm exp}(x)}{h}\right]$
$\displaystyle \phantom{f'(x) }= \lim_{h\rightarrow 0}\left[{\rm exp}(x)\dfrac{{\rm exp}(h)-1}{h}\right] = {\rm exp}(x)$
2.3 Notation for derivatives
Various notations are in common use for the derivative of a given function. Two such notations have already been introduced in this module and you will probably meet a third elsewhere. Here we provide a brief summary.
Function notation
This is the notation we have mainly used so far, in which a function is represented by f or f (x) or some similar symbol and its derivative (the derived function) is represented by f ′ or f ′ (x). This is a neat and compact notation but care is needed in handwritten work to make sure that the all–important prime (′) is clearly visible.
Leibniz notation i
This is the dy/dx notation that is especially popular among physicists. We will make much use of it in what follows.
If we let y = f (x), then in Leibniz notation the derivative is written $\dfrac{dy}{dx}(x)$ or $\dfrac{df}{dx}(x)$. i Sometimes these are abbreviated to $\dfrac{dy}{dx}$ (in which case it is assumed that we are regarding the variable y as a function y (x) of x), or $\dfrac{df}{dx}$ (in which case it is assumed that we are discussing a function f (x)).
An advantage of Leibniz notation is that it is also possible to write the derivative as
$\dfrac{d}{dx}[f(x)]$
so that for a specific function, f (x) = x2 say, we could write
$\dfrac{d}{dx}[x^2] = 2x$
Newtonian notation i
A different notation that is especially common in mechanics, but which will not be used in this module, uses a dot to denote derivatives. Thus, if x (t) represents the x coordinate of a moving particle at time t, then $\dot{x}(t)$ represents the rate of change of x with respect to time, i.e. the x component of the particle’s velocity.
✦ Given that y = f (x) = 1/x, and recalling Equation 7, determine the following:
(a) $\dfrac{dy}{dx}(2)$, (b) $\dfrac{df}{dx}(2a)$, (c) $\dfrac{d}{dt}\left(\dfrac1t\right)$, (d) f ′ (2 + 3x).
✧ We know from Equation 7 that if
$f(x) = 1/x$, then $f^{\prime} = -\dfrac{1}{x^2}$
so that
(a) $\dfrac{dy}{dx}(2) = -\dfrac{1}{2^2} = -\dfrac14$
(b) $\dfrac{dy}{dx}(2) = -\dfrac{1}{(2a)^2} = -\dfrac{1}{4a^2}$
(c) $\dfrac{dy}{dx}(\dfrac1t) =-\dfrac{1}{t^2}$
(d) $f^{\prime}(2+3x) = -\dfrac{1}{(2+3x)^2}$
3 Derivatives of simple functions
Now that the definitions are out of the way we can get down to the real business of doing calculus. The procedure by which derivatives are determined is called differentiation. In practice everybody who uses differentiation regularly, knows the derivatives of various standard functions (x, sin x, exp(x), etc.) and knows some simple rules for finding the derivatives of various combinations (sums, differences, products, quotients and reciprocals) of those standard derivatives. The formal definition of a derivative is rarely used in practice. This section introduces the standard derivatives and the basic rules for combining them.
3.1 Derivatives of basic functions
| f (x) | f ′ (x) |
|---|---|
| 1 | 0 |
| xn | nxn−1 |
| sin x | cos x |
| cos x | −sin x |
| tan x | sec2 x |
| cosec x | −cosec x cot x |
| sec x | sec x tan x |
| cot x | −cosec2 x |
| exp(x) | exp(kx) |
| log e (x) | 1/x |
| f (x) | f ′ (x) |
|---|---|
| k (constant) | 0 |
| kxn | nkxn−1 |
| sin kx | k cos kx |
| cos kx | −k sin kx |
| tan kx | k sec2 kx |
| cosec kx | −k cosec kx cot kx |
| sec kx | k sec kx tan kx |
| cot kx | −k cosec2 kx |
| exp(kx) | k exp(kx) |
| log e (kx) | 1/x |
Tables 1a and 1b list a number of functions with which you should already be familiar along with their derivatives. Each of these derivatives can be deduced from the definition given in the last section, though the proof is not always easy. If you are going to use calculus frequently you will need to know these derivatives or at least know where you can look them up quickly.
When using the tables it is important to remember the following points:
- n and k are constants.
- The functions in Table 1b are special cases of those in Table 1a, corresponding to k = 1.
- In each of the trigonometric functions x must be an angle in radians or a dimensionless real variable.
Question T4
Use the definition of the derivative to show that if f (x) = xn and n is a positive integer, then f ′ (x) = nxn−1. i
Answer T4
If f (x) = xn then, using the binomial theorem
f (x + h) = (x + h)n
f (x + h) = xn + nxn−1h + ½ n (n−1)xn−2h2 + ... + hn
So,$\dfrac{f(x+h)-f(x)}{h}$ = xn + nxn−1h + ½ n (n−1)xn−2h2 + ... + hn
All the terms except the first involve a positive power of h, so the limit of each of them is zero, giving the limit of right–hand side as nxn−1 as required. (This result holds true even when n is not a positive integer, but the above demonstration is not sufficiently general to prove that.)
The best way to get to know the standard derivatives is to use them frequently. Here are a few questions to start the process of familiarization.
✦ Find the derivatives (using Table 1) of the following functions:
(a) f (x) = x3, (b) g (t) = 1/t3, (c) $h(x) = \dfrac{1}{\sqrt[{\large\raise{2pt}5}]{x^2}}$
✧ In each case we express the function in the form xn so that we may apply the rule discussed in Question T4.
(a) For f (x) = x3 we have n = 3, so f ′ (x) = 3x3−1 = 3x2.
(b) If we rewrite g (t) = 1/t3 as g (t) = t−3, we have n = −3, so g ′ (t) = (−3)t−3−1 = −3t − 4 = −3/t4.
(c) If we rewrite $h(x) = \dfrac{1}{\sqrt[5]{x^2}}$ as $h(x) = \dfrac{1}{x^{2/5}} = x^{-2/5}$, we have $n = -\dfrac25$
so$h^{\prime}(x) = \left(-\dfrac25\right)x^{(-2/5)-1} = -\dfrac25x^{-7/5} = -\dfrac25\dfrac{1}{x^{7/5}} = -\dfrac25\dfrac{1}{\sqrt[{\large\raise{2pt}5}]{x^7\os}}$
✦ Which function in Table 1 is its own derivative?
✧ y = exp(x) has $\dfrac{dy}{dx} = {\rm {exp}}(x)$. (It is this property of the exponential function which makes it so important.)
Question T5
Find where the gradients of the tangents to the graph of y = sin x have the following values:
(a) 0, (b) −1, (c) +1. i
Answer T5
The gradient the graph of y = sin x at any value of x, is given by dy/dx = cos x (from Table 1).
(a) To find where the gradient is 0 we need to find the values of x for which cos x = 0; these are
$x = \pm\dfrac{\pi}{2}$, $\pm\dfrac{3\pi}{2}$, $\pm\dfrac{5\pi}{2}$, etc.
(b) In this case we need to solve cos x = −1, which gives x = ±π, ±3π, ±5π, etc
(c) In this case we need to solve cos x = +1, which gives x = 0, ±2π, ±4π, ±6π, etc.
Question T6
(a) Use your calculator (making sure that it is in radian mode) to investigate the limits
$\displaystyle \lim_{h\rightarrow 0} \left[\dfrac{\cos(h) - 1}{h}\right]$ and $\displaystyle \lim_{h\rightarrow 0} \left[\dfrac{\sin(h)}{h}\right]$
Using successively smaller values of h (e.g. h = ±0.1, ±0.01, etc.) try to estimate the limit in each case.
(b) Use the limits obtained in part (a) to find $\dfrac{d}{dx}(\sin x)$ from the general definition of the derived function.
[Hint Use the trigonometric identity sin(A + B) = sin A cos B + cos A sin B.]
Answer T6
(a) Table 2 shows approximate values of $\dfrac{\cos(h) - 1}{h}$ and $\dfrac{\sin(h)}{h}$ for various values of h.
| h | $\dfrac{\cos(h) - 1}{h}$ | $\dfrac{\sin(h)}{h}$ |
|---|---|---|
| 0.1 | −0.05 | 0.998 |
| −0.1 | 0.05 | 0.998 |
| 0.01 | −0.005 | 0.999 98 |
| −0.01 | 0.005 | 0.999 98 |
| 0.0001 | −0.000 05 | 0.999 999 998 |
| −0.0001 | 0.000 05 | 0.999 999 998 |
Thus it seems very likely that
$\displaystyle \lim_{h\rightarrow 0}\left[\dfrac{\cos(h)-1}{h}\right] = 0$ and $\displaystyle \lim_{h\rightarrow 0}\left[\dfrac{\sin(h)}{h}\right] = 1$
(These results are true, but we will not prove them rigorously.)
(b) f (x) = sin x, so f (x + h) = sin(x + h) and (using the hint)
$\dfrac{f(x+h)-f(x)}{h} = \dfrac{\sin(x+h)-\sin x}{h} = \dfrac{\sin x\cos h+\cos x \sin h - \sin x}{h}$
$\phantom{\dfrac{f(x+h)-f(x)}{h} }= \sin x\dfrac{\cos(h)-1}{h} + \cos x\dfrac{\sin h}{h}$
Since $\displaystyle \lim_{h\rightarrow 0}\left[\dfrac{\cos(h) - 1}{h}\right] = 0$ and $\displaystyle \lim_{h\rightarrow 0}\left[\dfrac{\sin(h)}{h}\right] = 1$
we obtain
$\displaystyle \lim_{h\rightarrow 0}\left[\dfrac{f(x+h)-f(x)}{h}\right] = (\sin x)\times 0 + (\cos x)\times 1 = \cos x$
In other words $\dfrac{d}{dx}(\sin x) = \cos x$
Question T7
Which functions in Table 1b have derivatives which are:
(a) always positive;
(b) always negative;
(c) can be positive or negative?
Answer T7
(a) The derivative of tan x is sec2 x which is always positive because it is a square. Since ex is always positive and is its own derivative, ex always has a positive derivative.
The last function with a positive derivative is loge x. This involves a tricky point. Since f (x) = loge x it is only defined for x > 0 so is its derivative, f ′ (x). In its domain f ′ (x) takes the same value as 1/x, and on this domain 1/x is positive. (Many authors prefer to discuss the function loge | x | since this function has 1/x as its derivative for all values of x ≠ 0).
(b) Since the derivative of cot x is −cosec2 x it is always negative.
(c) All the other derivatives in Table 1b can take both positive and negative values.
3.2 Derivative of a sum of functions
While it is possible, in theory, to find the derivative of any given function from the definition, this would in fact be an arduous process. In practice, those using calculus employ a set of simple rules which can be applied to combinations of functions to find the derivatives of a wide variety of functions with relative ease. The first of these simple rules is called the sum_rule_for_differentiationsum rule, which states:
The derivative of a sum of functions is the sum of the derivatives of the individual functions.
If f (x) and g (x) are two functions, this can be written as:
sum rule$\dfrac{d}{dx}[f(x)+g(x)] = \dfrac{d}{dx}[f(x)] + \dfrac{d}{dx}[g(x)]$(8) i
Alternatively we may write this rule in the form
[f (x) + g (x)]′ = f ′ (x) + g ′ (x) or just (f + g)′ = f ′ + g ′
This rule enables us to differentiate functions such as y = x1/2 + loge x. To do so we first note that it is the sum of two standard functions f (x) = x1/2 and g (x) = loge x, we then differentiate each of these functions and finally add the derivatives to obtain the required answer.
So, if
f (x) = x1/2 and g (x) = loge x
then, from Table 1
$\dfrac{df}{dx} = \dfrac12x^{-1/2}$ and $\dfrac{dg}{dx} = \dfrac1x$
so,$\dfrac{dy}{dx} = \dfrac{df}{dx} + \dfrac{dg}{dx} = \dfrac12x^{-1/2} + \dfrac1x$
and if $y = \sqrt{x\os}+\log_{\rm e}x$
then$\dfrac{dy}{dx} = \dfrac{1}{2\sqrt{x\os}} + \dfrac1x$ i
It is usually a good idea to think before applying the rule, as in the following question.
✦ Find the derivative of $h(x) = \dfrac{\cos x}{\sin x} + \dfrac{\sin x}{\cos x}$
✧ The function h (x) can be written as h (x) = cot 1x + tan x and is therefore a sum of two of the standard functions that appear in Table 1.
Let f (x) = cot x to obtain
f ′ (x) = −cosec2 x.
Let g (x) = tanx to obtain g ′ (x) = sec2 x.
Since h (x) = cot x + tan x we have
h ′ (x) = −cosec2 x + sec2 x.
The rule ‘derivative of a sum equals the sum of the derivatives’ applies equally well if more than two functions are added together. This allows us to obtain the derivatives of functions such as those in the following question.
Question T8
Use the sum rule to find dy/dx in each of the following cases:
(a) $y = 2 + \sqrt[{\large\raise{2pt}3}]{x\os} + {\rm e}^x$
(b) $y = \left(1+\sqrt{x\os}\right)^2$
(c) y = loge(xex)
(d) y = cot x sin x + tan x cos x
[Hint: write each function as a sum of functions appearing in Table 1.]
Answer T8
(a) $y=2+\sqrt[{\large\raise{2pt}3}]{x\os}+{\rm e}^x = 2+x^{1/3}+{\rm e}^x$ is the sum of three functions each belonging to Table 1.
So,
$\dfrac{dy}{dx} = \dfrac{d}{dx}\left(2+x^{1/3}+{\rm e}^x\right) = \dfrac{d}{dx}(2) + \dfrac{d}{dx}(x^{1/3}) + \dfrac{d}{dx}({\rm e}^x) = 0 + \dfrac13x^{-2/3}+{\rm e}^x = \dfrac13x^{-2/3}+{\rm e}^x$
(b) Expand $\left(1+\sqrt{x\os}\right)^2$ to find
$1 + 2\sqrt{x\os} + \left(\sqrt{x\os}\right)^2 = 1 + \sqrt{x\os} + \sqrt{x\os} + x$
(We have written $2\sqrt{x\os}$ as $\sqrt{x\os}+\sqrt{x\os}$ in order to express it as a sum of functions appearing in Table 1. In Subsection 3.3 another rule is developed which makes this unnecessary.)
Hence
$\dfrac{dy}{dx} = \dfrac{d}{dx}\left(1+\sqrt{x\os}\right)^2 = \dfrac{d}{dx}\left(1+\sqrt{x\os}+\sqrt{x\os}+x\right) = 0 + \dfrac12x^{-1/2} + \dfrac12x^{-1/2} + 1 = \dfrac{1}{\sqrt{x\os}} + 1$
(c) loge (x ex) = loge x + loge (ex) = loge x + x
Hence
$\dfrac{dy}{dx} = \dfrac{d}{dx}(\log_{\rm e}x\,{\rm e}^x) = \dfrac{d}{dx}(\log_{\rm e}x + x) = \dfrac1x + 1$
(d) $\cot x \sin x + \tan x \cos x = \dfrac{\cos x}{\sin x}\times \sin x + \dfrac{\sin x}{\cos x}\times \cos x = \cos x + \sin x$
Hence
$\dfrac{dy}{dx} = \dfrac{d}{dx}(\cot x \sin x + \tan x \cos x) = \dfrac{d}{dx}(\cos x + \sin x) = -\sin x + cos x$
Question T9
If you were to use the definition of the derived function (Equation 6)
$\displaystyle \dfrac{dy}{dx} = \lim_{h\rightarrow 0}\left[\dfrac{f(a + h) - f(a)}{h}\right]$(Eqn 6)
to show that the ‘derivative of the sum is the sum of the derivatives’, what assumption must you make about the limit of a sum?
Answer T9
You would have to assume (correctly, though we will not prove it) that the limit of a sum equals the sum of the limits.
3.3 Derivative of a constant multiple of a function
Table 1 gives the derivative of sin x, for example, but what about 2 sin x? In other words, what is the derivative of a constant times a function? The answer is given by the constant_multiple_rule_for_differentiationconstant multiple rule, which states:
The derivative of a constant times a function is equal to the constant times the derivative of the function.
Using k for the constant and f (x) for the function, this result can be written as:
constant multiple rule$\dfrac{d}{dx}[kf(x)] = k\dfrac{d}{dx}[f(x)]$(9) i
i.e. [k f (x)]′ = k f ′ (x) or just (k f)′ = k f ′
Therefore, for the above example,
$\dfrac{d}{dx}(2\sin x) = 2\dfrac{d}{dx}(\sin x) = 2\cos x$
similarly,$\dfrac{d}{dx}(\pi {\rm e}^x) = \pi\dfrac{d}{dx}({\rm e}^x) = \pi{\rm e}^x$
✦ Differentiate $h(x) = \left(x+\dfrac1x\right)^3$
✧ If we expand the function, we find
$\left(x+\dfrac1x\right)^3 = x^3+3x^2\times\dfrac1x+3x\times\dfrac{1}{x^2}+\dfrac{1}{x^3} = x^3+3x+\dfrac3x+\dfrac{1}{x^3} = x^3+3x+3x^{-1}+x^{-3}$
So$\dfrac{d}{dx}[h(x)] = \dfrac{d}{dx}[x^3+3x+3x^{-1}+x^{-3}] = 3x^2+3\times\dfrac{d}{dx}(x)+3\dfrac{d}{dx}(x^{-1})+(-3)x^{-4}$ i
$\phantom{\dfrac{d}{dx}[h(x)] } = 3x^2+3-\dfrac{3}{x^2}-\dfrac{3}{x^4}$
✦ Use the constant multiple rule to show that[f (x) − g (x)]′ = f ′ (x) − g ′ (x).
✧ We may certainly write
f (x) − g (x) = f (x) + (−1)g (x)
so, using the sum rule we may write
$\dfrac{d}{dx}[f(x)-g(x)] = \dfrac{d}{dx}[f(x)] + \dfrac{d}{dx}[(-1)g(x)]$
and using the constant multiple rule we can write
$\dfrac{d}{dx}[f(x)-g(x)] = \dfrac{d}{dx}[f(x)] - \dfrac{d}{dx}[g(x)]$
Thus[f (x) − g (x)]′ = f ′ (x) − g ′ (x)
This last result shows that the derivative of the difference of two functions is the difference of the derivatives, i.e.
$\dfrac{d}{dx}[f(x)-g(x)] = \dfrac{d}{dx}[f(x)] - \dfrac{d}{dx}[g(x)]$(10)
Question T10
Find the derivatives of the following functions: i
(a) $\left(\sqrt{x\os}-\dfrac{1}{\sqrt{x\os}}\right)^4$
(b) $\log_{\rm e}\sqrt[{\large\raise{2pt}3}]{x\os}$
(c) $\left(\sin\dfrac x2+\cos\dfrac x2\right)^2$
(d) $(\pi - x)^2$
(e) $\sin(x+2)$
(f) $\left[\tan\left(x + \dfrac{\pi}{4}\right)\right](1-\tan x)$
Hint $\tan(A+B) = \left(\dfrac{\tan A+\tan B}{1-\tan A\tan B}\right)$
Answer T10
(a) Expanding the bracket gives us
x2 − 4x + 6 − 4/x + 1/x2 = x2 − 4x + 6 − 4x−1 + x−2
So,$\dfrac{d}{dx}\left[\left(\sqrt{x\os} - \dfrac{1}{\sqrt{x\os}}\right)^4\right] = 2x-4-4(-1)x^{-2}+(-2)x^{-3} = 2x-4+4/x^2-2/x^3$
(b) $\log_{\rm e}\sqrt[{\large\raise{2pt}3}]{x^\vphantom{0}} = \log_{\rm e}x^{1/3} = \dfrac13\log_{\rm e}x$
So$\dfrac{d}{dx}\log_{\rm e}\sqrt[{\large\raise{2pt}3}]{x} = \dfrac{d}{dx}\left(\dfrac13\log_{\rm e}x\right) = \dfrac13\dfrac{d}{dx}\log_{\rm e}x = \dfrac{1}{3x}$
(c) $\left(\sin\dfrac x2+\cos\dfrac x2\right)^2 = \left(\sin\dfrac x2\right)^2 + 2\sin\dfrac x2\cos\dfrac x2 + \left(\cos\dfrac x2\right)^2$
Since sin2 A + cos2 A = 1, and 2 sin A cos A = sin(2A) for any angle A, this becomes 1 + sin x with the derivative
$\dfrac{d}{dx}(1+\sin x) = 0 + \cos x = \cos x$
(d) Expanding the bracket gives us
(π − x)2 = π2 − 2πx + x2
Now π2 is just a constant and so has a derivative of 0.
Therefore$\dfrac{d}{dx}\left[(\pi-x)^2\right] = 0 - 2\pi + 2x = -2(\pi-x)$
(e) sin(x + 2) does not appear in Table 1 so we need to expand it using sin(A + B) = sin A cos B + cos A sin B to find
sin(x + 2) = sin x cos 2 + cos x sin 2
Note that cos 2 and sin 2 are just constants, so the derivative is
$\dfrac{d}{dx}[\sin(x+2)] = \cos 2\dfrac{d}{dx}(\sin x)+\sin 2 \dfrac{d}{dx}(\cos x) = \cos 2\cos x - \sin 2 \sin x = \cos(x+2)$
(since cos(A + B) = cos A cosB − sin Asin B)
(f) Using $\tan(A + B) = \dfrac{\tan A + \tan B}{1 - \tan A\tan B}$ the function can be written as
$\dfrac{\tan x + \tan (\pi/4)B}{1 - \tan x\tan(\pi/4)}(1-\tan x)$
We can use tan(π/4) = 1 to simply this expression to tan x + tan(π/4) = 1 + tan x, which has the derivative sec2 x.
Question T11
If k is a constant and f (x) a function, write down the definition of f ′ (x) and [kf (x)]′. What assumption must you make about limits to justify the conclusion [kf (x)]′ = kf ′ (x)?
Answer T11
By definition
$\displaystyle f'(x) = \lim_{h\rightarrow 0}\left[\dfrac{f(x+h)-f(x)}{h}\right]$
So$\displaystyle [kf(x)]' = \lim_{h\rightarrow 0}\left[\dfrac{kf(x+h)-kf(x)}{h}\right]$
Therefore we can write:
$\displaystyle [kf(x)]' = \lim_{h\rightarrow 0}k\left[\dfrac{f(x+h)-f(x)}{h}\right] = \lim_{h\rightarrow 0}k\left[\dfrac{f(x+h)-f(x)}{h}\right] = k\lim_{h\rightarrow 0}\left[\dfrac{f(x+h)-f(x)}{h}\right] = kf'(x)$
We have assumed (correctly) that the limit of a constant multiple of an expression is the same as the constant multiple of the limit of the expression.
3.4 Derivative of a product of functions
This subsection introduces yet another way of combining functions and obtaining the derivative of the result. This is the product of two functions, f (x)g (x). Our aim is to express the derivative of such a product in terms of the derivatives of the functions f (x) and g (x) that are multiplied together to form the product, but the answer is not as obvious as it was for the sum or difference of functions. The ‘obvious’ answer that the derivative of a product is the product of the derivatives is wrong.
You cannot simply multiply derivatives.
To convince yourself of this consider f (x) = x2 and g (x) = x3.
Thenf (x)g (x) = x2x3 = x5.
We can differentiate each of these functions using Table 1.
thusf (x) = x2 implies f ′ (x) = 2x
g (x) = x3 implies g ′ (x) = 3x2
andf (x)g (x) = x5 implies [f (x)g (x)]′ = 5x4
Clearly, [f (x)g (x)]′ ≠ f ′ (x) × g ′ (x)
✦ Let f (x) = 2x and $g(x) = \dfrac{1}{4x}$
Find f ′ (x), g ′ (x), [f (x)g (x)]′ and show that [f (x)g (x)]′ ≠ f ′ (x) × g ′ (x).
✧ First we have $f^{\prime}(x) = 2$ and $g(x) = \dfrac{1}{4x} = \dfrac14x^{-1}$
so$g^{\prime}(x) = -\dfrac14x^{-2}$
Therefore
$f^{\prime}(x)\times g^{\prime}(x) = 2\times\left(-\dfrac{x^{-2}}{4}\right) = -\dfrac12x^{-2}$
However, $f(x)g(x) = 2x\times\dfrac{1}{4x} = \dfrac12$
and the derivative of this is
[f (x)g (x)]′ = 0
So in this case
[f (x)g (x)]′ ≠ f ′ (x) × g ′ (x)
The correct determination of[f (x)g (x)]′ involves not only f ′ (x) and g ′ (x) but also f (x) and g (x). It is given by the product_rule_of_differentiationproduct rule and is easier to express in symbols than in words:
product rule$\dfrac{d}{dx}[f(x)g(x)] = g(x)\dfrac{df}{dx} + f(x)\dfrac{dg}{dx}$(11) i
i.e.[f (x)g (x)]′ = f ′ (x)g (x) + f (x) g ′ (x) or just (fg)′ = f ′g + fg ′
The expression of this rule in terms of words is probably not very helpful:
The derivative of f times g equals the derivative of f times g plus f times the derivative of g.
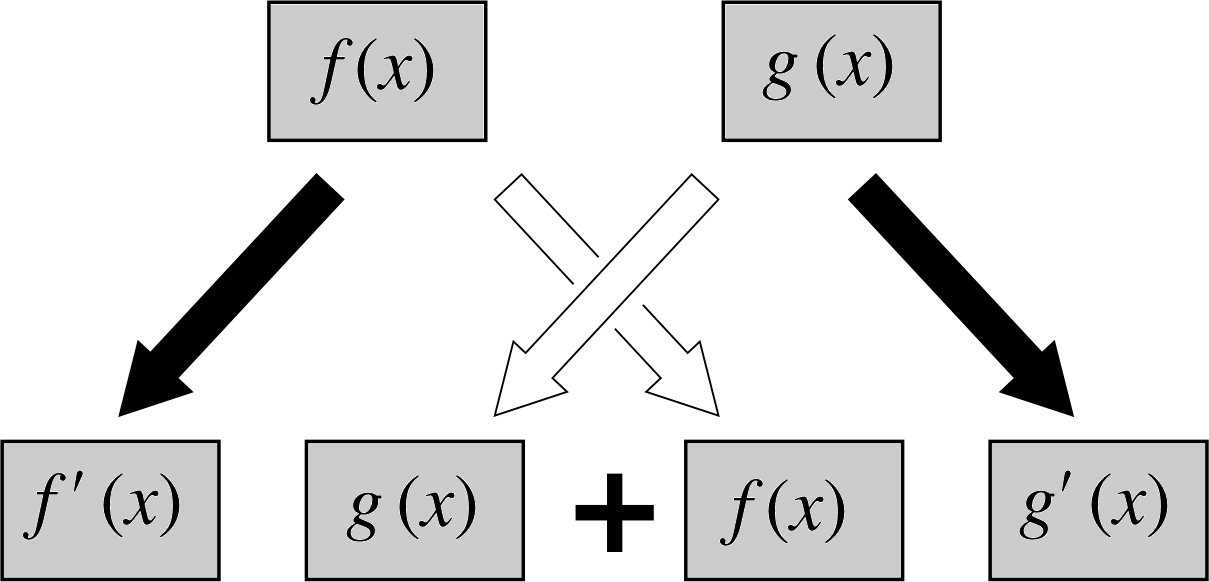
Figure 4 Differentiating a product of functions.
You may find Figure 4 a more useful memory aid.
In the case of f (x) = x2 and g (x) = x3 (discussed earlier) where f ′ (x) = 2x and g ′ (x) = 3x2
the application of the product rule to f (x)g (x) gives
[f (x)g (x)]′ = f ′ (x)g (x) + f (x) g ′ (x) = 2x × x3 + x2 × 3x2 = 2x4 + 3x4 = 5x4
and 5x4 is what we expect for the derivative of f (x)g (x) = x2x3 = x5.
✦ If f (x) = 2x and $g(x) = \dfrac{1}{4x}$ apply the product rule to find the derivative of f (x)g (x).
✧ $f(x) = 2x$ and $g(x) = \dfrac{1}{4x}$
so$f^{\prime}(x) = 2$ and $g^{\prime}(x) = -\dfrac{1}{4x^2}$
thus$[f(x)g(x)]^{\prime} = f^{\prime}(x)g(x) + f(x)g^{\prime}(x) = 2 \times \dfrac{1}{4x} + 2x\left(-\dfrac{1}{4x^2}\right) = \dfrac{1}{2x}-\dfrac{1}{2x} = 0$
which is correct since $f(x)g(x) = 2x\dfrac{1}{4x} =\dfrac12$ is a constant and has derivative zero.
Illustrations of the product rule
With the aid of the product rule we can now differentiate many more functions. The important step is to express the function that is to be differentiated in terms of the sum, difference or product of functions with known derivatives. Here are some examples.
Example 1
Differentiate 2 sin x cos x.
Solution
2 sin x cos x may be written as a product of the functions
f (x) = 2 sin x and g (x) = cos x for which f ′ (x) = 2 cos x and g ′ (x) = −sin x
Using the product rule
$\dfrac{d}{dx}[f(x)g(x)] = g(x)\dfrac{df}{dx} + f(x)\dfrac{dg}{dx}$(Eqn 11)
we can therefore write
$\dfrac{d}{dx}(2\sin x\cos x) = (2\cos x)(\cos x) + (2\sin x)(-\sin x) = 2(\cos^2x-\sin^2x)$ i
Example 2
Differentiate x ex + sec2 x.
Solution
x ex + sec2 x is the sum of two functions x ex and sec2 x, each of which is a product. So we differentiate xex first and then sec2 x (using the product rule for each) and then add the answers using the sum rule. First, x ex may be written as the product of the functions
f (x) = x and g (x) = ex for which f ′ (x) = 1 and g ′ (x) = ex
then, using the product rule
$\dfrac{d}{dx}[f(x)g(x)] = g(x)\dfrac{df}{dx} + f(x)\dfrac{dg}{dx}$(Eqn 11)
we can write
$\dfrac{d}{dx}(x{\rm e}^x) = {\rm e}^x \times \dfrac{d}{dx}x + x \times \dfrac{d}{dx}({\rm e}^x) = {\rm e}^x \times 1 + x \times {\rm e}^x = (1+x){\rm e}^x$
Second, sec2 x = sec x × sec x,
therefore f (x) = sec x and g (x) = sec x giving us f ′ (x) = sec x tan x and g ′ (x) = sec x tan x
Then, again using the product rule we find
$\dfrac{d}{dx}(\sec^2x) = (\sec x \tan x) \times (\sec x) + (\sec x) \times (\sec x\tan x) = 2\sec^2x\tan x$
Thus, combining these results, and using the sum rule we find
$\dfrac{d}{dx}(x{\rm e}^x + \sec^2x) = \dfrac{d}{dx}(x{\rm e}^x) + \dfrac{d}{dx}(\sec^2) = (1+x){\rm e}^x + 2\sec^2x\tan x$
✦ The kinetic energy of a particle of mass m moving with a speed v (t) that varies with time t, is m [v (t)]2/2.
Use the product rule
$\dfrac{d}{dx}[f(x)g(x)] = g(x)\dfrac{df}{dx} + f(x)\dfrac{dg}{dx}$(Eqn 11)
to show that the rate of change of m [v (t)]2/2 with time is $mv(t)\dfrac{dv}{dt}(t)$.
✧ Writing [v (t)]2 = v (t) × v (t), and using the product rule, we obtain
$\dfrac{d}{dt}[v(t)]^2 = v^{\prime}(t)v(t)+v(t)v^{\prime}(t) = 2v(t)v^{\prime}(t)$
Using the constant multiple rule, it follows that
$\dfrac{d}{dt}\left\{\dfrac12m[v(t)]^2\right\} = \dfrac12m\dfrac{d}{dt}\left\{[v(t)]^2\right\} = \dfrac12m[2v(t)v^{\prime}(t)] = mv(t)\dfrac{dv}{dt}(t)$
Question T12
Find the derivative of each of the following functions: i
(a) x2 loge x, (b) (sin x − 2 cos x)2, (c) $(1-\sqrt{x\os})(1+\sqrt[{\large\raise{2pt}3}]{x\os})$, (d) e2x, (e) sec x cot x, (f) x3F (x), where F (x) is an arbitrary function.
Answer T12
(a) If f (x) = x2 and g (x) = loge x, then
f (x)g (x) = x2 loge x
f ′ (x) = 2x and g ′ (x) = 1/x
So$\dfrac{d}{dx}(x^2\log_{\rm e}x) = 2x\log_{\rm e}x + x^2\times\dfrac1x = x(\log_{\rm e}x +1)$
(b) Frequently there is more than one way to break down the given function in terms of simpler functions the derivatives of which we know. In this exercise we could multiply out the brackets, but that would still involve using the product rule, so it is shorter to take
f (x) = (sin x − 2 cos x) and g (x) = (sin x − 2 cos x)
so that the given function is f (x)g (x), then
f ′ (x) = (cos x + 2 sin x) and g ′ (x) = (cos x + 2 sin x)
The derivative of the function f (x)g (x) is therefore
(cos x + 2 sin x)(sin x − 2 cos x) + (sin x − 2 cos x) × (cos x + 2 sin x) = 2 (cos x + 2 sin x)(sin x − 2 cos x)
(This sort of problem is better treated by another method known as the chain rule. This rule is discussed elsewhere in the differentiation block of FLAP.)
(c) This is probably a case where it is easier to expand the brackets and then differentiate, rather than to use the product rule directly. However, to use the product rule directly, put
$f(x) = 1 - \sqrt{x\os} = 1 - x^{1/2}$ and $g(x) = 1+\sqrt[{\large\raise{2pt}3}]{x} = 1 + x^{1/3}$
Therefore$f'(x) = -\frac12x^{-1/2}$ and $g'(x) = \frac13x^{-2/3}$
Therefore the derivative is
$(-\frac12x^{-1/2})(1+x^{1/3}) + (1-x^{1/2})\frac13x^{-2/3} = -\frac12x^{-1/2} - \frac56x^{-1/6}+\frac13x^{-2/3}$
(d) Take f (x) = ex and g (x) = ex then f ′ (x) = ex and g ′ (x) = ex
So$\dfrac{d}{dx}({\rm e}^{2x}) = {\rm e}^x\,{\rm e}^x + {\rm e}^x\,{\rm e}^x = 2\,{\rm e}^x$
as can be verified from Table 1.
(e) Using the product rule (and without thinking!) take
f (x) = sec x and g (x) = cot x
f ′ (x) = sec x tan x and g ′ (x) = −cosec2 x
The derivative of the product of f and g is
(sec x tan x) cotx + sec x (−cosec2 x) = sec x − sec x cosec2 x (using cot x = 1/tan x)
$= \sec x(1-\cosec^2x) = \dfrac{1}{\cos x}\left[1-\dfrac{1}{(\sin x)^2}\right] = \dfrac{(\sin^2x-1)}{\cos x\sin^2 x} = -\cosec x\cot x$
On the other hand you may have realized that
$\sec x\cot x = \dfrac{1}{\cos x}\dfrac{\cos x}{\sin x} = \cosec x$
and from Table 1 the derivative of cosec x is −cosec x cot x. A little thought can often save a lot of hard work!
(f) Putting f (x) = x2 and g (x) = F (x) we have
$\dfrac{d}{dx}\left[x^3F(x)\right] = 3x^2F(x) + x^3F'(x)$
Question T13
The instantaneous motion of a particle moving along a straight line (call it the x–axis) can be described, at time t, in terms of its displacement sx(t) from a fixed reference position, its velocity vx(t) and its acceleration ax(t). i
These quantities are defined in such a way that
$a_x(t) = \dfrac{dv_x}{dt}(t)$ and $v_x(t) = \dfrac{ds_x}{dt}(t)$
If the displacement is given as a function of time by
sx(t) = [cos(ωt) − 2 sin(ωt)] exp(αt) where ω and α are constants
show that ax(t) = 2αvx(t) − (ω2 + α2)sx(t)
Answer T13
There are several ways to tackle this question, but the following is probably the easiest.
$v_x(t) = \dfrac{d}{dt}\left[s_x(t)\right] = \dfrac{d}{dt}\left\{[\cos(\omega t) - 2\sin(\omega t)]{\rm exp}(\alpha t)\right\}$
From the product rule we can write this as
$= \dfrac{d}{dt}\left\{[\cos(\omega t) - 2\sin(\omega t)]\right\}\times {\rm exp}(\alpha t) + [\cos(\omega t) - 2\sin(\omega t)]\dfrac{d}{dt}{\rm exp}(\alpha t)$
= [−ω sin(ωt) − 2ω cos(ωt)] exp(αt) + α [cos(ωt) − 2 sin(ωt)] exp(αt)
so,vx (t) = ω [−sin(ωt) − 2 cos(ωt)] exp(αt) + αsx (t)
Differentiating both sides of the last equation with respect to t we find
$a_x(t) = \dfrac{d}{dx}v_x(t)$
$\phantom{a_x(t) }= \dfrac{d}{dt}\left\{\omega[-\sin(\omega t)-2\cos(\omega t)]{\rm exp}(\alpha t)\right\}+\alpha\dfrac{d}{dt}s_x(t)$
$\phantom{a_x(t) }= \omega^2[-\cos(\omega t) + 2\sin(\omega t)]{\rm exp}(\alpha t) + \omega\alpha[-\sin(\omega t) -2\cos(\omega t)]{\rm exp}(\alpha t) + \alpha v_x(t)$
We can now use the original specification for sx (t) to eliminate [−cos(ωt) + 2 sin(ωt)] exp(αt) from the above equation, and we can use the formula for vx (t) to eliminate ω [−sin(ωt) − 2 cos(ωt)] exp(αt) from the same equation by writing
ω [−sin(ωt) − 2 cos(ωt)] exp(αt) = vx (t) − αsx (t)
Consequently, we obtain
ax(t) = −ω2sx(t) + α [vx (t) − sx(t)] + αvx (t) = 2αvx (t) − (ω2 + α2)sx(t)
Question T14
This question extends the product rule
$\dfrac{d}{dx}[f(x)g(x)] = g(x)\dfrac{df}{dx} + f(x)\dfrac{dg}{dx}$(Eqn 11)
to three functions.
If f (x), g (x), h (x) are any three functions, show that
$\dfrac{d}{dx}[f(x)g(x)h(x)] = f'(x)g(x)h(x) + f(x)g'(x)h(x)+f(x)g(x)h'(x)$
Answer T14
To make use of the product rule we need to write f (x)g (x)h (x) as the product of the two functions f (x)g (x) and h (x). Then
$\dfrac{d}{dx}[f(x)g(x)h(x)] = \dfrac{d}{dx}[f(x)g(x)]h(x) + f(x)g(x)\dfrac{d}{dx}h(x) = f '(x)g(x)h(x) + f (x)g'(x)h(x) + f (x)g(x)h'(x)$
Question T15
Use the result developed in Question T14 to find
$\dfrac{d}{dx}({\rm e}^x\log_{\rm e}x\sin x)$
Answer T15
Take f (x) = ex, g (x) = loge x and h (x) = sin x
then f ′gh + fg ′h + fgh ′ = ex loge x sin x + ex(1/x) sin x + ex loge x cos x
3.5 Derivative of a quotient of functions
It is frequently the case that we need to find the derivative of the quotient $\dfrac{f(x)}{g(x)}$ of two functions f (x) and g (x).
i The derivative of a quotient, like that of a product, depends not only on the values of f ′ (x) and g ′ (x), but also on f (x) and g (x). The quotient_rule_of_differentiationquotient rule states:
quotient rule$\dfrac{d}{dx}\left[\dfrac{f(x)}{g(x)}\right] = \dfrac{g(x)\cfrac{df}{dx}-f(x)\dfrac{dg}{dx}}{\left[g(x)\right]^2}$(12) i
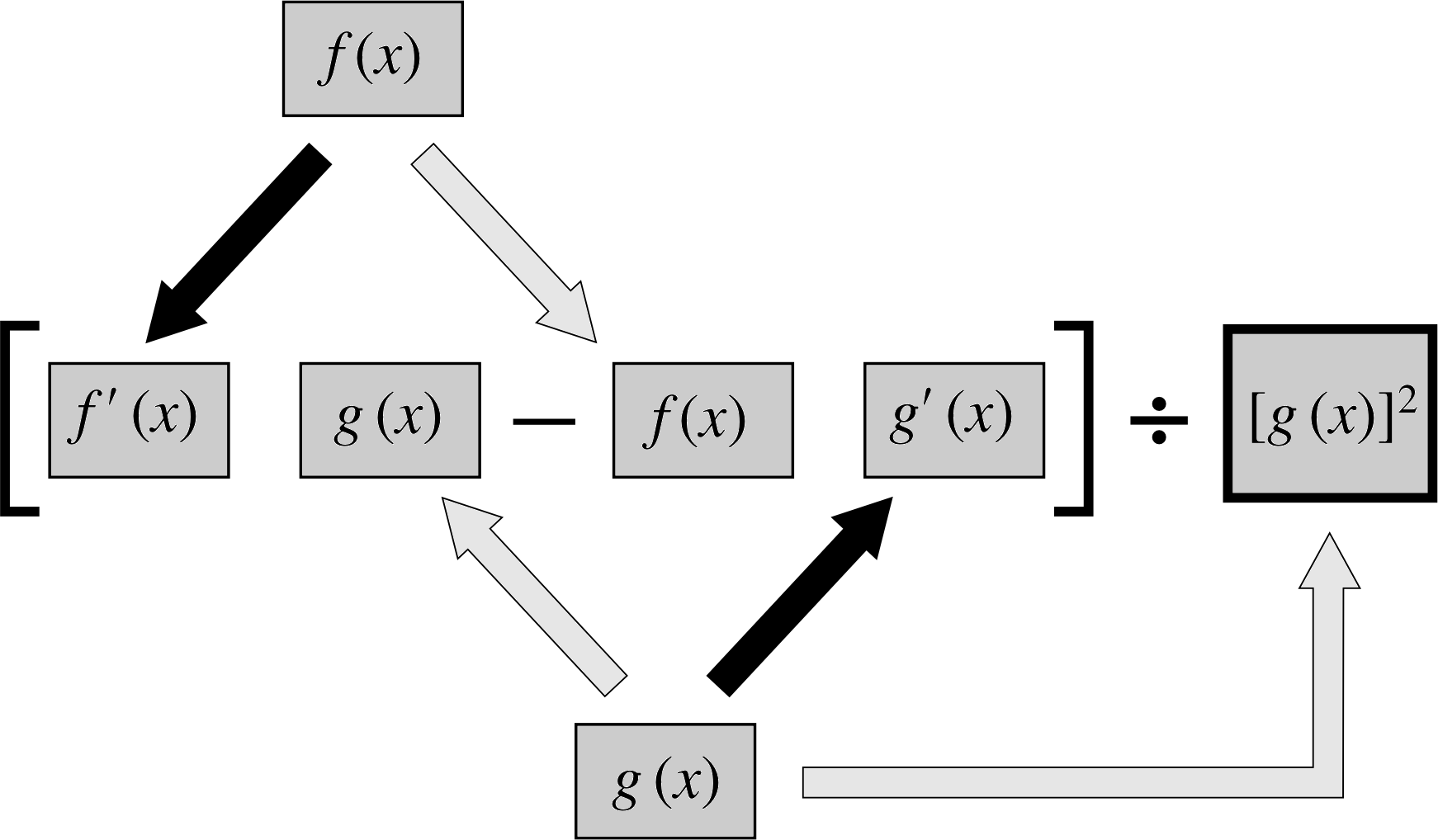
Figure 5 The quotient rule.
i.e.$\left[\dfrac{f(x)}{g(x)}\right]' = \dfrac{f'(x)g(x) - f(x)g'(x)}{\left[g(x)\right]^2}$ or just $\left(\dfrac fg\right) = \dfrac{f' g - fg'}{g^2}$
You may find Figure 5 a useful memory aid.
To apply this result to the function
$y = \dfrac{\sin x}{x}$
take f (x) = sin x and g (x) = x so that f ′ (x) = cos x and g ′ (x) = 1
Then$\dfrac{dy}{dx} = \dfrac{(\cos x)x-(\sin x)\times 1}{x^2} = \dfrac{x\cos x-\sin x}{x^2}$ i
✦ Write y = x3 as x5/x2 and use the quotient rule to find dy/dx.
✧ Set $f(x) = x^5$ and $g(x) = x^2$
then $f^{\prime}(x) = 5x^4$ and $g^{\prime}(x) = 2x$
and$\dfrac{dy}{dx} = \dfrac{f^{\prime}(x)g(x) - f(x)g^{\prime}(x)}{[g(x)]^2} = \dfrac{(5x^4)(x^2)-(x^5)(2x)}{(x^2)^2} = \dfrac{5x^6-2x^6}{x^4} =3x^2$
(and from Table 1 we know that the derivative of x3 is 3x2, so we have verified that the quotient rule gives the correct answer in this particular case).
✦ Use the quotient rule to find $\dfrac{d}{dx}\left[\dfrac{1}{F(x)}\right]$ in terms of f ′ (x) and F (x).
✧ Putting f (x) = 1 and g (x) = F (x) in the quotient formula, we obtain the reciprocal_rule_of_differentiationreciprocal rule
$\dfrac{d}{dx}\left[\dfrac{1}{F(x)}\right] = -\dfrac{F^{\prime}(x)}{[F(x)]^2}$
You may find this useful, but there is no point in remembering it if you know the quotient rule since it is just a special case of that more general rule.
Question T16
Find dy/dx in each of the following cases:
(a) $y = \dfrac{x}{{\rm e}^x}$ (b) $y = \dfrac{1-x^2}{\cos x}$ (c) $y = \dfrac{x^5-x^4+x^3-x^2}{(x+1)^2}$ (d) $y = \dfrac{x\log_{\rm e}}{\tan x}$
Answer T16
(a) Set f (x) = x and g (x) = ex, to give y = f (x)/g (x).
Now, f ′ (x) = 1 and g ′ (x) = ex, so that the quotient rule gives us
$\dfrac{dy}{dx} = \dfrac{1\times{\rm e}^x-x\times{\rm e}^x}{\left({\rm e}^x\right)^2} = \dfrac{{\rm e}^x(1-x)}{{\rm e}^{2x}} = \dfrac{1-x}{{\rm e}^x}$
(b) Set f (x) = 1 − x2 and g (x) = cos x, to give y = f (x)/g (x).
Now, f ′ (x) = −2x and g ′ (x) = −sin x, so that the quotient rule gives us
$\dfrac{dy}{dx} = \dfrac{(-2x)(\cos x)-(1-x^2)(-\sin x)}{\cos^2 x} = \dfrac{-2x\cos x+(1-x^2)\sin x}{\cos^2 x}$
(c) Set f (x) = x5 − x4 + x3 − x2 and g (x) = (x + 1)2. To apply the quotient rule we need to differentiate (x + 1)2 which is easiest done if we expand it to obtain x2 + 2x + 1.
Thus f ′ (x) = 5x4 − 4x3 + 3x2 − 2x and g ′ (x) = 2x + 2.
So$\dfrac{dy}{dx} = [(5x^4-4x^3+3x^2-2x)(x+1)^2-(x^5-x^4+x^3-x^2)(2x+2)]/(x+1)^4$
$\phantom{\dfrac{dy}{dx} }= [(5x^4-4x^3+3x^2-2x)(x+1)-2(x^5-x^4+x^3-x^2)]/(x+1)^3$
$\phantom{\dfrac{dy}{dx} }= \dfrac{x(3x^4+3x^3-3x^2+3x-2)}{( x + 1)^3}$
(d) With f (x) = x loge x and g (x) = tan x, we can apply the quotient rule. As an intermediate stage we differentiate f (x) using the product rule.
$f'(x) = x\dfrac1x+1\times\log_{\rm e}x = 1 + \log_{\rm e}x$
$g'(x) = \sec^2x$
$\dfrac{dy}{dx} = \dfrac{(1+\log_{\rm e}x)\tan x - x\log_{\rm e}x\sec^2x}{\tan^2 x}$
Question T17
If f (x) = (x − 1)2 and g (x) = xex, find the following:
(a) $\dfrac{d}{dx}\left[f(x)-g(x)\right]$ (b) $\dfrac{d}{dx}\left[f(x)g(x)\right]$ (c) $\dfrac{d}{dx}\left[\dfrac{f(x)}{g(x)}\right]$ (d) $\dfrac{d}{dx}\left[\dfrac{g(x)}{f(x)}\right]$ i
Answer T17
(a) f (x) − g (x) = (x − 1)2 − x ex = x2 − 2x + 1 − x ex
$\dfrac{d}{dx}[f(x)-g(x)] = 2x - 2 - (x\,{\rm e}^x + 1\times{\rm e}^x) = 2x -2 -(x+1)\,{\rm e}^x$
(b) $\dfrac{d}{dx}[f(x)g(x)] = \dfrac{d}{dx}[(x-1)^2x\,{\rm e}^x]$
= (2x − 2)x ex + (x − 1)2ex + (x − 1)2x ex
= (x − 1) ex(x2 + 2x − 1)
(c) $\dfrac{f(x)}{g(x)} = \dfrac{(x-1)^2}{x{\rm e}^x}$
f ′ (x) = (2x − 2) = 2 (x − 1)
g ′ (x) = x ex + ex = (x + 1) ex
$\dfrac{d}{dx}\left[\dfrac{f(x)}{g(x)}\right] = \dfrac{2(x-1)x\,{\rm e}^x-(x-1)^2(x+1)\,{\rm e}^x}{x^2{\rm e}^{2x}} = \dfrac{(x-1)(1+2x-x^2)}{x^2{\rm e}^x}$
(d) This can certainly be done using the quotient rule, but we can also obtain the answer from the reciprocal rule (i.e. Equation 13) and the solution to part (c) of this question as follows. First we let $F(x) = \dfrac{f(x)}{g(x)}$ so that, from the reciprocal rule
$\dfrac{d}{dx}\left[\dfrac{g(x)}{f(x)}\right] = \dfrac{d}{dx}\left[\dfrac{1}{F(x)}\right] = -\dfrac{F'(x)}{\left[F(x)\right]^2}$
$\phantom{\dfrac{d}{dx}\left[\dfrac{g(x)}{f(x)}\right] }= -\dfrac{(x-1)(1+2x-x^2)}{x^2\,{\rm e}^x} \left/\left[\dfrac{f(x)}{g(x)}\right]^2\right.$ (from part (c)
$\phantom{\dfrac{d}{dx}\left[\dfrac{g(x)}{f(x)}\right] }= -\dfrac{(x-1)(1+2x-x^2)}{x^2\,{\rm e}^x}\times\left[\dfrac{x\,{\rm e}^x}{(x-1)^2}\right]^2$
$\phantom{\dfrac{d}{dx}\left[\dfrac{g(x)}{f(x)}\right] }= \dfrac{(x^2-2x-1)\,{\rm e}^x}{(x-1)^3}$
The aim of the next question is to derive the quotient rule from the product rule. It begins by showing how to obtain the reciprocal rule without using the quotient rule.
Question T18
(a) Let f (x) be an arbitrary function and let h (x) = 1/f (x) so that
f (x)h (x) = 1
Differentiate both sides of this equation and hence obtain a formula for $\dfrac{d}{dx}\left[\dfrac{1}{f(x)}\right]$
(similar to that given in Equation 13):
the reciprocal rule$\dfrac{d}{dx}\left[\dfrac{1}{F(x)}\right] = -\dfrac{F^{\prime}(x)}{[F(x)]^2}$(Eqn 13)
(b) Let f (x) and g (x) be any two functions, and write $\dfrac{f(x)}{g(x)} = f(x) \times \dfrac{1}{g(x)}$, then use the answer to part (a) and the product rule (Eqn 11)
$\dfrac{d}{dx}[f(x)g(x)] = g(x)\dfrac{df}{dx} + f(x)\dfrac{dg}{dx}$(Eqn 11)
to derive the quotient rule
$\dfrac{d}{dx}\left[\dfrac{f(x)}{g(x)}\right] = \dfrac{g(x)\cfrac{df}{dx}-f(x)\dfrac{dg}{dx}}{\left[g(x)\right]^2}$(Eqn 12)
Answer T18
(a) Differentiating both sides of the following equation
f (x)h (x) = 1
using the product rule, we obtain
f ′ (x)h (x) + f (x)h ′ (x) = 0
Using the fact that $h(x) = \dfrac{1}{f(x)}$, this can be rearranged to give
$h'(x) = -\dfrac{f'(x)h(x)}{f(x)} = -\dfrac{f'(x)}{\left[f(x)\right]^2}$
and, since $h'(x) = \dfrac{d}{dx}\left[\dfrac{1}{f(x)}\right]$, we have obtained the required result.
(b) Differentiating $f(x) \times \dfrac{1}{g(x)}$ using the product rule, we have
$\dfrac{d}{dx}\left[f(x)\times \dfrac{1}{g(x)}\right] = f'(x)\times\dfrac{1}{g(x)} + f(x)\dfrac{d}{dx}\left[\dfrac{1}{g(x)}\right]$
$\phantom{\dfrac{d}{dx}\left[f(x)\times \dfrac{1}{g(x)}\right] }= \dfrac{f'(x)}{g'(x)} + f(x)\times\left\{-\dfrac{g'(x)}{\left[g(x)\right]^2}\right\}$
$\phantom{\dfrac{d}{dx}\left[f(x)\times \dfrac{1}{g(x)}\right] }= \dfrac{f'(x)g(x) - f(x)g'(x)}{\left[g(x)\right]^2}$
Question T19
Use $\dfrac{d}{dx}(\sin x) = \cos x$, $\dfrac{d}{dx}(\cos x) = -\sin x$, and the quotient rule
$\dfrac{d}{dx}\left[\dfrac{f(x)}{g(x)}\right] = \dfrac{g(x)\cfrac{df}{dx}-f(x)\dfrac{dg}{dx}}{\left[g(x)\right]^2}$(Eqn 12)
to differentiate (a) tan x, and (b) cot x.
Answer T19
(a) f (x) = sin x and g (x) = cos x
so, f ′ (x) = cos x and g ′ (x) = −sin x
thus$\dfrac{d}{dx}(\tan x) = \dfrac{d}{dx}\left(\dfrac{\sin x}{\cos x}\right) = \dfrac{(\cos x)(\cos x)-(\sin x)(-\sin x)}{\cos^2x}$
$\phantom{\dfrac{d}{dx}(\tan x) }= \dfrac{\cos^2x+\sin^2x}{\cos^2x} = \dfrac{1}{\cos^2x} = \sec^2x$ (since cos2 x + sin2 x = 1)
(b) To differentiate $\cot x = \dfrac{\cos x}{\sin x}$
letf (x) = cos x and g (x) = sin x
so, f ′ (x) = −sin x and g ′ (x) = cos x
Then
$\dfrac{d}{dx}(\cot x) = \dfrac{(-\sin x)(\sin x)-(\cos x)(\cos x)}{\sin^2x} = \dfrac{-1}{\sin^2x} = -\cosec^2x$
Question T20
(a) Use the reciprocal rule
$\dfrac{d}{dx}\left[\dfrac{1}{F(x)}\right] = -\dfrac{F^{\prime}(x)}{[F(x)]^2}$(Eqn 13)
to find $\dfrac{d}{dx}({\rm e}^{-x})$.
(b) The function $f(x) = \dfrac12({\rm e}^x + {\rm e}^{-x})$ is sometimes known as the hyperbolic_function_identitieshyperbolic cosine of x (and is denoted by cosh x).
Find $\dfrac{df}{dx}$ and show that $\left[f(x)\right]^2 - \left(\dfrac{df}{dx}\right)^2 = 1$.
Answer T20
(a) $f(x) = {\rm e}^{-x} = \dfrac{1}{{\rm e}^x} = \dfrac{1}{g(x)}$ where g (x) = ex
Since g ′ (x) = e we have $f'(x) = -\dfrac{{\rm e}^x}{\left({\rm e}^x\right)^2} = -\dfrac{1}{{\rm e}^x} = -{\rm e}^{-x}$
(b) f (x) is a constant multiple of a sum of two functions, so, using our rules and the result of part (a),
$\dfrac{df}{dx} = \dfrac12({\rm e}^x-{\rm e}^{-x})$
(The function $\dfrac12({\rm e}^x-{\rm e}^{-x})$ is known as the hyperbolic_function_identitieshyperbolic sine of x and denoted by sinh x).
$\left[f(x)\right]^2 - \left(\dfrac{df}{dx}\right)^2 = \dfrac14({\rm e}^x+{\rm e}^{-x})^2 - \dfrac14({\rm e}^x-{\rm e}^{-x})^2 = \dfrac14\left[({\rm e}^{2x}+2+{\rm e}^{-2x})-({\rm e}^{2x}-2+{\rm e}^{-2x})\right] = 1$
thus establishing the useful result that:
cosh2 x − sinh2 x = 1
Question T21
Let $F(x) = \dfrac{Mm}{(x-a)^2}$ where G, M, m and a are constants. Find f ′ (x).
Answer T21
F (x) is proportional to the reciprocal of (x − a)2 and
$\dfrac{d}{dx}(x-a)^2 = \dfrac{d}{dx}(x^2-2ax+a^2) = 2x-2a = 2(x-a)$
Hence, using the reciprocal rule,
$F'(x) = -GMm\dfrac{2(x-a)}{(x-a)^4} = -\dfrac{2GMm}{(x-a)^3}$
Question T22
Using $\dfrac{d}{dx}(\sin x) = \cos x$ and $\dfrac{d}{dx}(\cos x) = -\sin x$, along with the reciprocal rule
$\dfrac{d}{dx}\left[\dfrac{1}{F(x)}\right] = -\dfrac{F^{\prime}(x)}{[F(x)]^2}$(Eqn 13)
find the derivatives of (a) sec x and (b) cosec x.
Answer T22
(a) $\sec x = \dfrac{1}{\cos x}$
so$\dfrac{d}{dx}\left(\dfrac{1}{\cos x}\right) = -\dfrac{(-\sin x)}{\cos^2x} = \dfrac{1}{\cos x} \times \dfrac{\sin x}{\cos x} = \sec x\tan x$
(b) $\cosec x = \dfrac{1}{\sin x}$
so$\dfrac{d}{dx}\left(\dfrac{1}{\sin x}\right) = \dfrac{(-\cos x)}{\sin^2x} = -\dfrac{1}{\sin x} \times \dfrac{\cos x}{\sin x} = -\cosec x\cot x$
4 More about logarithmic and exponential functions
4.1 Why exp(x) is considered to be special
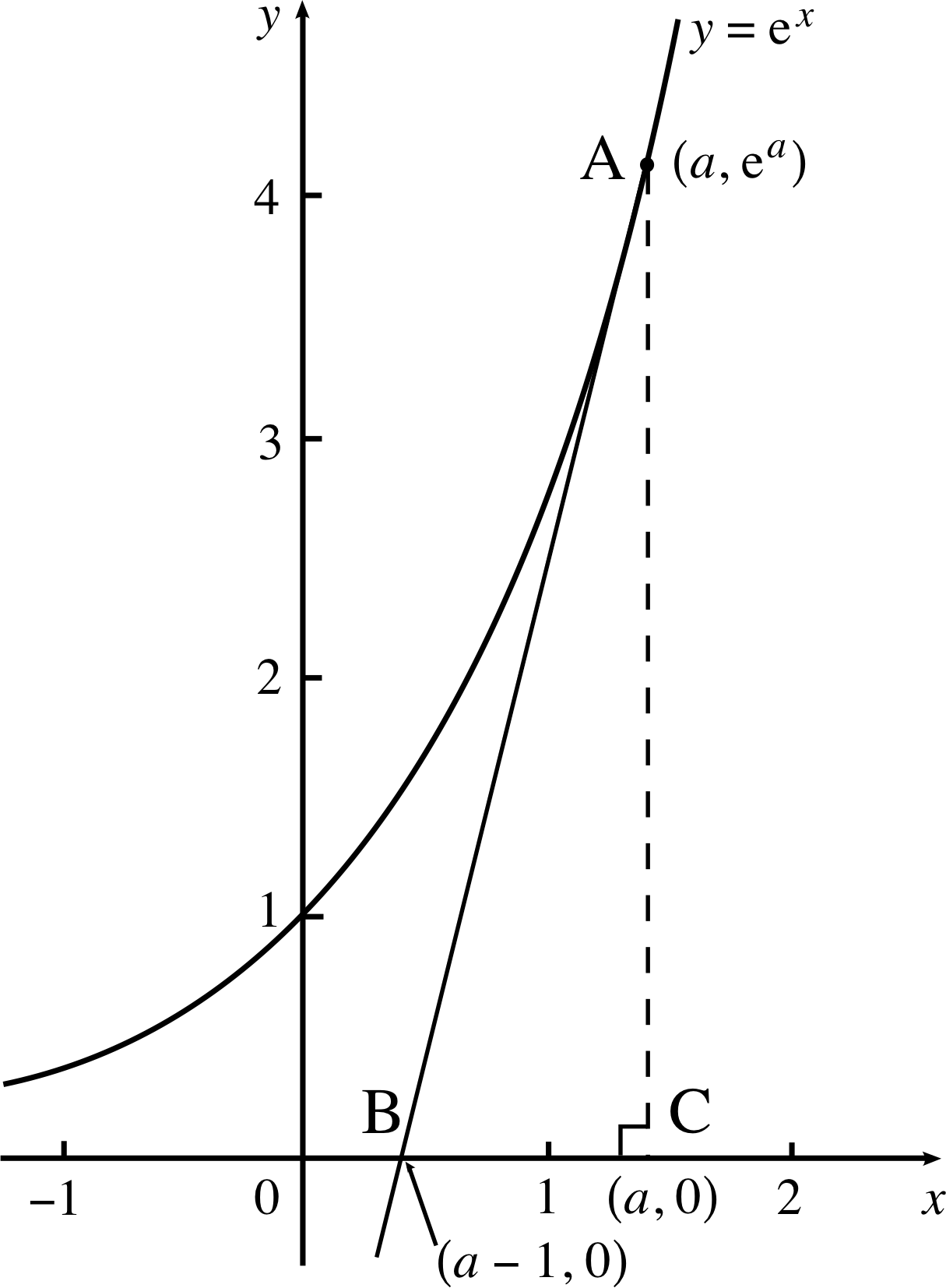
Figure 6 The graph of y = ex.
Of all the functions listed in Table 1, f (x) = exp(x) = ex is the only one which is its own derivative. Far from being a technical curiosity this fact turns out to be of great significance and ultimately explains why the exponential function plays such an important role in physics. i
It also has an interesting interpretation in terms of the graph of y = ex, shown in Figure 6. Since f ′ (x) = ex the gradient of the tangent to the graph at the point A which has coordinates x = a and y = ea is f ′ (a) = ea which is the same as the height of A above C.
So the rate of change of f (x) when x = a is simply f (a), that is, the rate of change of the exponential function at any point is equal to the value of 3 the function itself at that point. In Figure 6 the point B has coordinates (a − 1, 0). Since A is the point (a, ea), the line AB has a gradient of
$\dfrac{\rm CA}{\rm BC} = \dfrac{{\rm e}^a}{1} = {\rm e}^a$
and is therefore the tangent to the graph at A. So, to draw a tangent to y = ex at (a, ea), simply join (a, ea) to (a − 1, 0) and the resulting line is bound to have a gradient of ea.
✦ Is f (x) = ex the only function which is its own derivative? (Think about the rules of differentiation that you already know.)
✧ No. The derivative of a constant multiple of a function is the constant multiple times the derivative, so we have
$\dfrac{d}{dx}(A{\rm e}^x) = A{\rm e}^x$ for any constant A
Thus, any constant multiple of the exponential function, such as Aex, is its own derivative. However, apart from functions of this kind there are no other functions that are their own derivatives. i
✦ Using the product rule
$\dfrac{d}{dx}[f(x)g(x)] = g(x)\dfrac{df}{dx} + f(x)\dfrac{dg}{dx}$(Eqn 11)
find the derivatives of (a) e2x, (b) e3x, (c) e4x.
Deduce the formula for the derivative of enx where n is any positive integer.
✧ (a) Since e2x = ex × ex the product rule gives
$\dfrac{d}{dx}({\rm e}^{2x}) = 2{\rm e}^{2x}$
(b) e3x = ex × e2x,
so$\dfrac{d}{dx}({\rm e}^{3x}) = {\rm e}^{x}\times 2{\rm e}^{2x} + {\rm e}^{x}{\rm e}^{2x} = 3{\rm e}^{3x}$
(c) e4x = e2x × e2x = e2x × 2e2x + 2e2x e2x = 4e4x
Therefore, generally, if n is any positive integer
$\dfrac{d}{dx}({\rm e}^{nx}) = n{\rm e}^{nx}$
A similar result holds true even when n is not a positive integer. This was given in Table 1, but it deserves to be emphasized again here.
$\dfrac{d}{dx}({\rm e}^{kx}) = k{\rm e}^{kx}$ for any constant k(14)
Question T23
If $y = \dfrac{C{\rm e}^x}{1 + C{\rm e}^x}$ for some constant C, show that $\dfrac{dy}{dx} = y(1-y)$
Answer T23
You should have been able to establish this result using the quotient rule, but the following method, known as implicit differentiation, requires a little less algebra. (This method is explored more fully elsewhere in FLAP, see the Glossary for details.)
First write y (1 + Cex) = Cex
Differentiate both sides, using the product rule on the left–hand side
y ′ (1 + Cex) + yCex = Cex
Now eliminate (1 + Cex) by writing $(1 + C{\rm e}^x) = \dfrac{C{\rm e}^x}{y}$, and divide the resulting equation through by Cex to get the required result
$\dfrac{y'}{y} + y = 1$ so $y' = y(1 - y)$
(Notice that by using y ′ in this way we have avoided the need to differentiate y explicitly, hence the name implicit differentiation.)
Question T24
Differentiate f (x) = (ex + e−x)(ex − e−x).
Answer T24
$\dfrac{d}{dx}\left[({\rm e}^x+{\rm e}^{-x})({\rm e}^x-{\rm e}^{-x})\right] = \dfrac{d}{dx}\left({\rm e}^{2x}-{\rm e}^{-2x}\right) = 2{\rm e}^{2x} + 2{\rm e}^{-2x}$
4.2 Derivative of ax
The previous subsection considered the derivative of ex. However, functions such as 2x and πx sometimes arise in physical applications, and so it is necessary to know how to differentiate any function of the form ax, where the positive number a being raised to the power x is not necessarily e. As an example we will consider the differentiation of 2x, but the method is of general applicability. First note that exp is the inverse function of loge, this means that exp reverses the effect of loge so that
eloge 2 = exp(loge 2) = 2
since2 = exp(loge 2) 2x = [exp(loge 2)]x = exp(x loge 2)
So, $\dfrac{d}{dx}\left(2^x\right) = \dfrac{d}{dx}\left[\exp(\log_{\rm e}2)\right]^x$
Now, from Equation 14 (or Table 1) we know that $\dfrac{d}{dx}({\rm e}^{kx}) = k{\rm e}^{kx}$ for any constant k
and, if we choose k to be loge 2, this gives us
$\dfrac{d}{dx}(2^x) = \dfrac{d}{dx}[\exp(x\log_{\rm e}2)] = (\log_{\rm e}2)[\exp(x\log_{\rm e}2)] = (\log_{\rm e}2)2^x$
A similar argument applies with any positive number, a say, in place of 2. So we have the result:
$\dfrac{d}{dx} (a^x) = (\log_{\rm e}a)a^x$ (a > 0)(15)
Rather than trying to remember this result you would probably be wiser to try to remember the method that was used to obtain it. Notice the way that the properties of exponentials and logarithms have been used to express a function of the form ax in terms of ekx, and how the simple properties of ekx have then been exploited.
✦ Find $\dfrac{d}{dx}(\pi^x)$
✧ Here a = π so the derivative is (loge π)πx
✦ Apply the formula for differentiating ax
$\dfrac{d}{dx}({\rm e}^{kx}) = k{\rm e}^{kx}$ for any constant k(Eqn 14)
when a = e.
✧ The result is (loge a)ax and if a = e then, since loge e = 1, we have
$\dfrac{d}{dx}({\rm e}^x) = {\rm e}^x$
as before.
Question T25
Differentiate each of the following functions: (a) f (x) = 3x, (b) f (x) = 3x−1, (c) f (x) = (2 + 3)x, (d) f (x) = 2xex.
Answer T25
(a) (loge 3)3x
(b) (loge 3)3x−1 (if we write 3x−1 = 3x/3)
(c) (loge 5)5x
(d) $\dfrac{d}{dx}\left(2^x\,{\rm e}^x\right) = \dfrac{d}{dx}\left[(2\,{\rm e}^x\right] = \left[\log_{\rm e}(2{\rm e})\right](2{\rm e})^x = \left(1+\log_{\rm e}2\right)2^x\,{\rm e}^x$
4.3 Derivative of loga x
As stated in Table 1:
$\dfrac{d}{dx}(\log_{\rm e}x) = \dfrac1x$
From this it is easy to deduce the derivative of loge kx, where k is a constant
loge (kx) = loge k + loge x
so$\dfrac{d}{dx}(\log_{\rm e}(kx)) = \dfrac{d}{dx}(\log_{\rm e}k) + \dfrac{d}{dx}(\log_{\rm e}x) = \dfrac1x$ i
If we had been compelled to differentiate log10 x or log2 x the problem would have been a little more difficult, but still not intractable. The general method for differentiating logs to an arbitrary base, such as loga x is remarkably similar to that for dealing with ax: it involves expressing loga x in terms of loge x which can be differentiated easily. As an example, let us consider log10 x. To express it in terms of loge x we write
y = log10 x
then x = 10y
and, taking logarithms to the base e of both sides of this equation, we obtain
loge x = loge(10y) = y loge 10
and recalling that y = log10 x this can be rearranged to give
$y = \log_{10}x = \dfrac{\log_{\rm e}x}{\log_{\rm e}10}$ i
We may now easily differentiate log10 x because 1/loge 10 is a constant, so
$\dfrac{d}{dx}(\log_{10}x) = \dfrac{d}{dx}\left(\dfrac{\log_{\rm e}x}{\log_{\rm e}10}\right) = \left(\dfrac{1}{\log_{\rm e}10}\right)\dfrac{d}{dx}(\log_{\rm e}x) = \left(\dfrac{1}{\log_{\rm e}10}\right)\times \dfrac1x = \dfrac{1}{x\log_{\rm e}10}$
A similar argument applies for any positive base a giving the general result:
$\dfrac{d}{dx}(\log_a x) = \dfrac{1}{x\log_{\rm e}a}$(16) i
✦ If a = e, check that the above formula gives our previous result for the derivative of loge x.
✧ $\dfrac{d}{dx}(\log_a x) = \dfrac{1}{x\log_{\rm e} a}$
If a = e then loge e = 1, and the result is 1/x as expected.
✦ Differentiate logπ x.
✧ From Equation 16,
$\dfrac{d}{dx}(\log_\pi x) = \dfrac{1}{x\log_{\rm e}\pi}$(Eqn 16)
$\dfrac{d}{dx}(\log_\pi x) = \dfrac{1}{x\log_{\rm e}\pi}$
Question T26
Differentiate each of the following functions:
(a) f (x) = log2 x
(b) f (x) = log10 x2
(c) f (x) = $\dfrac{\log_2 x}{\log_{10}x}$ [Hint: loga b = (loga c)(logcb)]
(d) f (x) = ax loga x where a is a positive constant.
Answer T26
(a) $\dfrac{d}{dx}(\log_2 x) = \dfrac{1}{x\log_e 2}$
(b) $\dfrac{d}{dx}(\log_{10}x^2) = \dfrac{d}{dx}(2\log_{10}x) = \dfrac{2}{x\log_{\rm e} 10}$
(c) The answer is zero, which is seen most easily by putting $\dfrac{\log_2 x}{\log_{10}x} = \log_2 10$, so we are simply required to differentiate a constant.
(d) $\dfrac{d}{dx}(a^x\log_a x) = (a^x\log_{\rm e}a)\times \log_a x + a^x\times \dfrac{1}{x\log_{\rm e}a} = a^x\left(\log_{\rm e}x+\dfrac{1}{x\log_{\rm e}a}\right)$
if we use (loge a) × (loga x) = loge x.
4.4 Resisted motion under gravity: an example
Imagine a parachutist falling to Earth with velocity, vx (t) downwards, at time t. For convenience we will choose the positive x–axis to be the downward vertical, with the origin at the point where the parachute opens. The parachutist is subject to two forces, gravity acting downwards and the resistance of the air on his parachute acting upwards. Suppose that the resistive force is proportional to [vx (t)]2 with a constant of proportionality k (which has to be determined experimentally). It follows from Newton’s second law that the equation governing the motion is
$m\dfrac{d}{dx}[v_x(t)] = mg - k[v_x(t)]^2$(17)
where m is the mass of the parachutist and g is the magnitude of the acceleration due to gravity. The forces on the right–hand side have opposite sign because they act in opposite directions.
Now, suppose you want to check that the following expression for vx (t) satisfies Equation 17,
$v_x(t) = \sqrt{\dfrac{mg}{k}}\left[\dfrac{1+B\exp(-2t\sqrt{gk/b})}{1-B\exp(-2t\sqrt{gk/b})}\right]$(18)
where B is a constant (determined by the speed of the parachutist at time t = 0). It appears that we must first differentiate vx (t), which is a rather complicated multiple of the quotient of two functions. We could certainly proceed directly, and just differentiate the function as it stands, but a little thought should tell you that the algebra is going to get very nasty; so it is worth trying to simplify the expression. To simplify the notation let $A = \sqrt{mg/k}$ and $\alpha = 2\sqrt{gk/m}$, and let us write vx rather than vx (t). So we have a simplified version of Equation 18,
$v_x = A\left[\dfrac{1+B\exp(-\alpha t)}{1-B\exp(-\alpha t)}\right]$(19)
Now, using the quotient rule,
$\dfrac{d}{dx}\left[\dfrac{f(x)}{g(x)}\right] = \dfrac{g(x)\cfrac{df}{dx}-f(x)\dfrac{dg}{dx}}{\left[g(x)\right]^2}$(Eqn 12)
to differentiate this equation with respect to t, we find:
$\dfrac{dv_x}{dt} = A\left\{\dfrac{\left[\dfrac{d}{dt}(1+B\exp^{-\alpha t})\right](1-B\exp^{-\alpha t}) - \left[\dfrac{d}{dt}(1-B\exp^{-\alpha t})\right](1+B\exp^{-\alpha t})}{(1-B\exp^{-\alpha t})^2}\right\}$
$\phantom{\dfrac{dv_x}{dt}} = A\left[\dfrac{(-B\alpha\exp^{-\alpha t})(1-B\exp^{-\alpha t}) - (B\alpha\exp^{-\alpha t})(1+B\exp^{-\alpha t})}{(1-B\exp^{-\alpha t})^2}\right]$
$\phantom{\dfrac{dv_x}{dt}} = A\left[\dfrac{(-B\alpha\exp^{-\alpha t}+B^2\alpha\exp^{-2\alpha t}) - (B\alpha\exp^{-\alpha t}+B^2\alpha\exp^{-2\alpha t})}{(1-B\exp^{-\alpha t})^2}\right]$
$\phantom{\dfrac{dv_x}{dt}} = A\left[\dfrac{-2B\alpha\exp^{-\alpha t}}{(1-B\exp^{-\alpha t})^2}\right]$
Substituting this expression for dvx (t)/dt into the left–hand side of Equation 17 and using the fact that Aα = 2g we obtain
$mA\left[\dfrac{-2B\alpha\exp^{-\alpha t}}{(1-B\exp^{-\alpha t})^2}\right] = \dfrac{-4mgB{\rm e}^{-\alpha t}}{(1-B{\rm e}^{-\alpha t})^2}$
and substituting the same expression for dvx (t)/dt into the right–hand side of Equation 17 and using the fact that kA2 = mg we obtain
$mg - mg\left(\dfrac{1+B\exp^{-\alpha t}}{1-B\exp^{-\alpha t}}\right)^2 = mg\left[\dfrac{(1-B\exp^{-\alpha t})^2 - (1+B\exp^{-\alpha t})^2}{(1-B\exp^{-\alpha t})^2}\right] = \dfrac{-4mgB{\rm e}^{-\alpha t}}{(1-B{\rm e}^{-\alpha t})^2}$
Thus, the two sides of Equation 17 are indeed equal if vx has the form given in Equation 18.
This really completes the differentiation and subsequent manipulation, but having introduced an expression (Equation 18) for the downward velocity under gravity in the presence of a resistive force it is worth noting at least one of its mathematical properties:
✦ What is the behaviour of vx (t) as t becomes large? In other words, what is $\displaystyle \lim_{t\rightarrow \infty}\left[v_x(t)\right]$?
✧ As t becomes large Be−αt becomes small, and the velocity approaches the value
$\sqrt{\dfrac{mg}{k}\os}\dfrac{1+0}{1-0} = \sqrt{\dfrac{mg}{k}}$
This final constant value of the velocity is called the terminal velocity. Its existence is a striking feature of resisted motion.
✦ What is the terminal velocity if m = 80 kg, k = 30 kg m−1 and g = 9.81 m s−2?
✧ Terminal velocity = $\sqrt{\dfrac{mg}{k}} = \sqrt{\dfrac{(80\,{\rm kg})\times(9.81\,{\rm m\,s^{-2}})}{(30\,{\rm kg\,m^{-1}})}}$ ≈ 5.1 m s−1
Question T27
Show that $y = \dfrac{\log_{\rm e}2-x}{\log_{\rm e}2+x}$ satisfies the equation
$2y'(x)\log_{\rm e}2+[1+y(x)]^2$
Answer T27
Since $y(x) = \dfrac{\log_{\rm e}2-x}{\log_{\rm e}2+x}$ we have, from the quotient rule,
$\dfrac{d}{dx}\left[y(x)\right] = \dfrac{d}{dx}\left(\dfrac{\log_{\rm e}2-x}{\log_{\rm e}2+x}\right) = \dfrac{-1\times(\log_{\rm e}2+x)-(\log_{\rm e}2-x)\times 1}{(\log_{\rm e}2+x)^2} = \dfrac{-2\log_{\rm e}2}{(\log_{\rm e}2+x)^2}$
It follows that
$2(\log_{\rm e}2)y'(x)+[1+y(x)]^2 = 2(\log_{\rm e}2)\dfrac{-2\log_{\rm e}2}{(\log_{\rm e}2+x)^2} + \left(1 + \dfrac{\log_{\rm e}2-x}{\log_{\rm e}2+x}\right)^2$
which (eventually) simplifies to zero, so the expression y (x) satisfies the equation.
5 Closing items
5.1 Module summary
- 1
-
A function, f say, is a rule that assigns a single value of the dependent variable, y say, (in the codomain) to each value of the independent variable x in the domain of the function, such that y = f (x).
- 2
-
The rate of change, or derivative of a function f (x) at x = a, can be interpreted as the gradient of the graph of the function at the point x = a. Some standard derivatives are given in Table 1a (repeated here for reference).
- 3
-
The derivative is defined more formally in terms of a limit, and may be represented in a variety of ways. If y = f (x)
$\displaystyle f'(x) = \dfrac{dy}{dx} = \lim_{h\rightarrow 0}\left(\dfrac{\Delta y}{\Delta x}\right) = \lim_{h\rightarrow 0}\left[\dfrac{f(x + h) - f(x)}{h}\right]$
- 4
-
The sum, constant multiple, product and quotient rules for differentiating combinations of functions are as follows:
Table 1a Some standard derivatives. f (x) f ′ (x) k (constant) 0 kxn nkxn−1 sin kx k cos kx cos kx −k sin kx tan kx k sec2 kx cosec kx −k cosec kx cot kx sec kx k sec kx tan kx cot kx −k cosec2 kx exp(kx) k exp(kx) log e (kx) 1/x sum rule(f + g)′ = f ′ + g ′
constant multiple rule(k f)′ = kf ′
product rule(fg)′ = f ′g + fg ′
quotient rule$\left(\dfrac fg\right)' = \dfrac{f' g-gf'}{g^2}$
- 5
-
The derivatives of the standard functions are given in Table 1a.
- 6
-
The derivatives of ax and loga x are given by
$\dfrac{d}{dx}(a^x) = (\log_{\rm e}a)a^x$(Eqn 15)
and$\dfrac{d}{dx}(\log_a x) = \dfrac{1}{x\log_{\rm e}a}$(Eqn 16)
- 7
-
You should be aware that logarithms to different bases are related by
loga b = (loga c)(logc b)
5.2 Achievements
Having completed the module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Define the derivative of a function (at a point) as a limit and give the definition a graphical interpretation.
- A3
-
Use the definition of the derivative as a limit to calculate the derivative of simple functions.
- A4
-
Know the derivatives of a range of standard functions.
- A5
-
Use addition, subtraction, multiplication and division to express a given function in terms of ‘simpler’ ones in appropriate cases.
- A6
-
Differentiate a constant multiple of a function.
- A7
-
Apply the rule for differentiating the sum (and difference) of functions.
- A8
-
Apply the product rule of differentiation.
- A9
-
Apply the quotient rule of differentiation.
- A10
-
Use the properties of logarithms and exponentials to determine the derivatives of loga x and ax.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A1, A2 and A4)
Write down the derivative of f (x) = loge x. As x increases from zero how does the gradient of the tangent to the graph change? What is the behaviour of loge x as x approaches infinity?
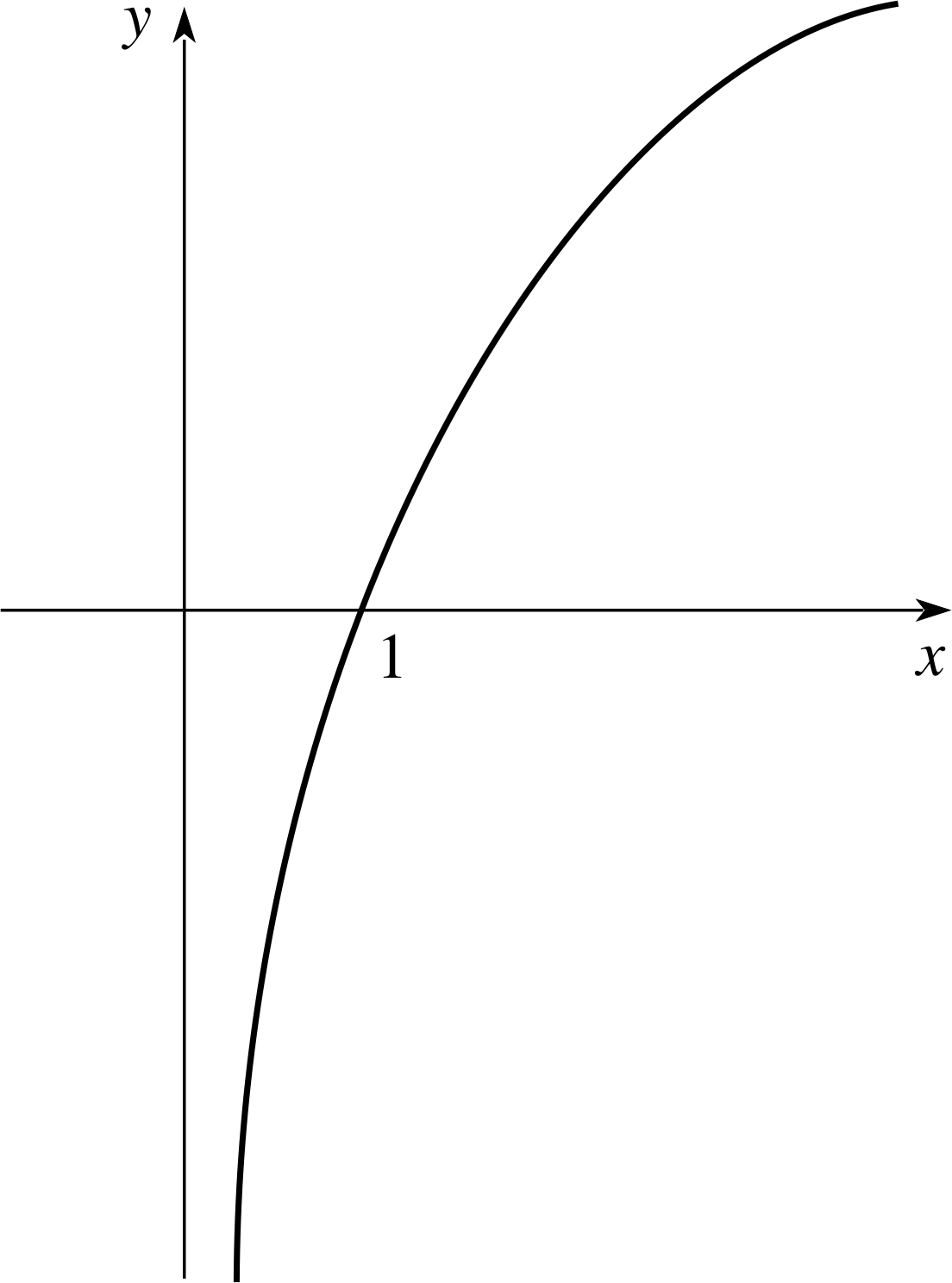
Figure 8 See Answer E1.
Answer E1
$\dfrac{d}{dx}\left(\log_{\rm e}x\right) = \dfrac1x$
For x positive and close to 0 the tangent has a large positive gradient. As x becomes increasingly positive, the gradient of the tangent decreases, approaching 0 as x approaches infinity. The graph of y = loge x is given in Figure 8.
loge x approaches +∞ as x → ∞ even though its rate of growth (its derivative) approaches 0.
(Reread Subsection 2.2Subsections 2.2 and Subsection 3.13.1 if you had difficulty with this question.)
Question E2 (A3)
Using the definition of the derivative as a limit, differentiate f (x) = 1/x2.
Answer E2
We need to evaluate the limit of $\dfrac{f(x+h)-f(x)}{h}$ as h→∞
Now$\dfrac{f(x+h)-f(x)}{h} = \dfrac1h\left[\dfrac{1}{(x+h)^2}-\dfrac{1}{x^2}\right] = \dfrac1h\left[\dfrac{x^2-(x+h)^2}{(x+h)^2x^2}\right] = \dfrac1h\left[\dfrac{-2hx-h^2}{(x+h)^2x^2}\right] = \dfrac{-2x-h}{(x+h)^2x^2}$
As h approaches 0 the numerator approaches −2x while the denominator approaches x2 × x2 = x4. Hence
$\dfrac{d}{dx}\left(\dfrac{1}{x^2}\right) = \dfrac{-2x}{x^4} = -\dfrac{2}{x^3}$
(Reread Subsection 2.2Subsections 2.2 and Subsection 2.32.3 if you had difficulty with this question.)
Question E3 (A4, A5 and A6)
Find dy/dx for each of the following functions:
(a) y = 2x (x − 1)(x + 2)
(b) y = sin(x + π/4) [Hint: sin(A + B) = sin A cos B + cos A sin B]
(c) y = loge x2
Answer E3
(a) y = 2x (x − 1)(x + 2) = 2x (x2 + x − 2) = 2x3 + 2x2 − 4x
so$\dfrac{dy}{dx} = 6x^2+4x-4$
(b) Using sin(A + B) = sin A cos B + cos A sin B, we can rewrite the equation as
y = sin x cos(π/4) + cos x sin(π/4)
so$\dfrac{dy}{dx} = \cos x\cos(\pi/4)-\sin x\sin(\pi/4) = \dfrac{1}{\sqrt{2\os}}(\cos x - \sin x )$
which is equal to $\cos\left(x + \dfrac{\pi}{4}\right)$
(c) y = loge x2 = 2 loge x and therefore $\dfrac{dy}{dx} = \dfrac2x$
(Reread Subsection 3.1, Subsection 3.23.2 and Subsection 3.33.3 if you had difficulty with this question.)
Question E4 (A4 to A9)
Find f ′ (x) for each of the following functions:
(a) f (x) = x cos x + x2 sin x
(b) f (x) = $\left(x-\dfrac1x\right)^2{\rm e}^x$
(c) f (x) = $\dfrac{1+x+x^2}{1-x^2}$
(d) f (x) = $\dfrac{\sqrt{x\os}\sin x}{\log_{\rm e}x}$
(e) f (x) = $\dfrac{{\rm exp}(x+\log_{\rm e}x)}{\sqrt{x\os}}$
(f) f (x) = axxa
Answer E4
(a) f ′ (x) = cos x + x (−sin x) + 2x sin x + x2 cos x = (1 + x2) cos x + x sin x
(b) $\dfrac{d}{dx}\left(x - \dfrac1x\right)^2 = \dfrac{d}{dx}(x^2 - 2 + x^{-2}) = 2x − 2x^{-3} = 2x(1 - x^{-4})$
So$f'(x) = 2x(1-x^{-4}){\rm e}^x + \left(x-\dfrac1x\right)^2{\rm e}^x$
(c) $f'(x) = \dfrac{(1+2x)(1-x^2)-(1+x+x^2)(-2x)}{(1-x^2)^2} = \dfrac{1+4x+x^2}{(1-x^2)^2}$
(d) $\dfrac{d}{dx}(\sqrt{x\os}\sin x) = \dfrac12x^{-1/2}\sin x+\sqrt{x\os}\cos x$
So$f'(x) = \dfrac{\left(\frac12x^{-1/2}\sin x +\sqrt{x\os}\cos x\right)\log_{\rm e}x-\left(\sqrt{x\os}\sin x\right)\big(1/x\big)}{\left(\log_{\rm e}x\right)^2} = \dfrac{1}{2\sqrt{x\os}}\dfrac{\left(\sin x + 2x\cos x\right)\log_{\rm e}x-2\sin x}{\left(\log_{\rm e}x\right)^2}$
(e) $f(x) = \dfrac{{\rm e}^x{\rm e}^{\log_{\rm e}x}}{\sqrt{x\os}} = \dfrac{x{\rm e}^x}{\sqrt{x\os}} = \sqrt{x\os}{\rm e}^x$
So$f'(x) = \dfrac12x^{-1/2}{\rm e}^x + \sqrt{x\os}^x$
(f) f ′ (x) = (loge a) ax × xa + ax × axa−1 = (loge a) ax × xa + ax−1xa−1
(Reread Sections 3 and 4 if you had difficulty with this question.)
Question E5 (A4, A5, A6, A8 and A9)
If n is a positive integer, the series
$1+x+x^2+x^3+\dots+x^n$ has the sum $\dfrac{x^{n+1}-1}{x-1}$
show that the sum of the series
$1+2x+x^2+3x^2+\dots+nx^{n-1}$ is $\dfrac{nx^{n+1}-(n+1)x^n+1}{(x-1)^2}$ i
Answer E5
We are told that $\dfrac{x^{n+1}-1}{x-1} = 1 + x + x^2+\dots+x^n$
Differentiating the right–hand side gives the required series
1 + 2x + 3x2 + ... + nxn−1
which must be the same as the derivative of the left–hand side
$\dfrac{d}{dx}\left(\dfrac{x^{n+1}-1}{x-1}\right) = \dfrac{(n+1)x^n(x-1)-(x^{n+1}-1)}{(x-1)^2} = \dfrac{(n+1)x^{n+1}-(n+1)x^n-x^{n+1}+1}{(x-1)^2} = \dfrac{nx^{n+1}-(n+1)x^n+1}{(x-1)^2}$
(This question required thought in addition to a knowledge of differentiation. If you spotted the need to find the derivative but had difficulty finding the derivative, reread Subsection 3.1Subsections 3.1, Subsection 3.23.2 and Subsection 3.43.4.)
Question E6 (A7 and A8)
If f and g are functions show that
$\left(\dfrac{1}{f(x)g(x)}\right)' = \left(\dfrac{1}{f(x)}\right)'\dfrac{1}{g(x)} + \dfrac{1}{f(x)}\left(\dfrac{1}{g(x)}\right)'$
Answer E6
It is certainly possible to differentiate both sides, using the reciprocal rule, and then to show that the results are equal. However, this result is merely the product rule when applied to the functions 1/f and 1/g, and no working is necessary. (A salutary lesson confirming that a little thought can sometimes save a lot of work.)
(Reread Subsection 3.4Subsections 3.4 and Subsection 3.53.5 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection. Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.