MATH 2.7: Vector product of vectors |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Many of the most useful mathematical models that arise in physics involve vectors, and so we must be able to manipulate vector quantities in order to derive useful information from these models. The branch of mathematics that deals with the manipulation of vectors is known as vector algebra, and the purpose of this module is to introduce one aspect of this topic – the concept and use of the vector product. More elementary aspects of vector algebra are dealt with elsewhere in FLAP, as is the other type of product of two vectors – the scalar product.
In Section 2 of this module, the vector (or cross) product is defined and its various properties are deduced. The section concludes by showing how the product may be expressed in terms of the Cartesian unit vector and ordered triple notations.
In Section 3, the scalar triple product and vector triple product are introduced, and the fundamental identities for each triple product are discussed and derived.
In Section 4 we discuss examples of various physical quantities which can be related or defined by means of vector products. Considered in this discussion are the relationships between angular_momentumangular and linear momentum, torque and force, and magnetic force and magnetic field. The section concludes with a discussion of the Hall effect which depends on the balancing of electric and magnetic forces on moving charge carriers.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to Ready to study? in Subsection 1.3.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Find a vector of magnitude 5 units which is perpendicular to both vectors a and b, where a = 2 i − j + 3 k, and b = i + 4 j − 2 k.
Answer F1
By taking the vector product (a × b), we obtain a vector normal to both a and b, in the direction of advance of a right–hand screw. Therefore the required vector can be in this direction or the opposite direction, i.e. it can be along either ±(a × b). If we divide (a × b) by its own magnitude we obtain the required unit vector parallel to (a × b):
$\pm\dfrac{5(\boldsymbol{a\,\times\,b})}{\lvert\,\boldsymbol{a\,\times\,b}\,\rvert}$
Nowa × b = (2 i − j + 3 k) × (i + 4 j − 2 k)
so that a × b = 8 k + 4 j + k + 2 i + 3 j − 12 i = −10 i + 7 j + 9 k
and therefore | a × b | = $\sqrt{100 + 49 + 81\os} = \sqrt{230\os}$ so that the required vector is
$\pm\dfrac{5}{\sqrt{230\os}}$(−10 i + 7 j + 9 k) ≈ ±(−3.30 i + 2.31 j + 2.97 k)
Question F2
The position vector of a particle P relative to point O is given by r = (2, −1, 1) m. The particle has a mass m of 0.60 kg and a velocity υ given by υ = (1, 2, −1) m s−1.
(a) Find the angular momentum of P about O.
(b) If a force F is applied to P, determine the torque on P about O, given that F = (3, −1, 2) N.
Answer F2
(a) The angular momentum is
m (r × υ) = 0.60 (2, −1, 1) × (1, 2, −1) kg m2 s−2
m (r × υ) = 0.60 (1 − 2, 2 + 1, 4 + 1) kg m2 s−2
m (r × υ) = 0.60 (−1, 3, 5) kg m2 s−2
m (r × υ) = (−0.60, 1.8, 3.0) kg m2 s−2
(b) The torque is
r × F = [(2, −1, 1) × (3, −1, 2)] N m = (−1, −1, 1) N m
1.3 Ready to study?
Study comment It is assumed that you already have some basic knowledge of vector algebra. You should be familiar with the Cartesian unit vector and ordered triple notations for the representation of vector quantities. Also, you should understand the use of these notations in operations such as scaling_of_a_vectorscaling, vector addition and vector_differencevector subtraction, and in determining the magnitude_of_a_vector_or_vector_quantitymagnitude of a vector. Furthermore, you should be familiar with the concept of the scalar product of two vectors, and the techniques of vector algebra relevant to the scalar product. Terms such as acceleration, electric charge, electric field, force, momentum, position vector, component_of_a_vectorcomponent (of a vector) and velocity are used, and you should understand how to apply Newton’s laws of motion. It is assumed also, that you are familiar with basic mathematical concepts including the ideas of Cartesian coordinate systems, and the use of trigonometric functions and differentiation. Some knowledge of determinants would be an advantage, since it would make some of the formulae a little easier to remember, but it is not essential. (You should talk to your tutor if you wish to learn about determinants since this topic is not discussed in FLAP.) In the last section you will need to know that the magnitude of the (centripetal_accelerationcentripetal) acceleration of a particle moving round a circle of radius r is υ2/r towards the centre of the circle. If you are uncertain about any of these terms, then you can review them by reference to the Glossary, which will indicate where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
If A = (7 i − j + 5 k) and B = (4 i + j − k) determine A − B, | A − B | and the unit vector in the same direction as A − B.
Answer R1
Subtracting B from A:
A − B = (7 i − j + 5 k) − (4 i + j − k) = 3 i− 2 j + 6 k so that
| A − B | = $\sqrt{3^2+(-2)^2+ 6^2} = \sqrt{49\os} = 7$
Therefore the required unit vector is $\dfrac37\,{\boldsymbol i} - \dfrac27\,{\boldsymbol j} + \dfrac67\,{\boldsymbol k}$
Consult vector_differencevector subtraction and unit vector in the Glossary for further information.
Question R2
A particle of mass 2 kg is acted on by forces F1 and F2 simultaneously. Determine the acceleration of the particle given that F1 = (2, −3, 1) N and F2 = (2, 9, −3) N.
Answer R2
The resultant force F acting on the particle is given by
F = F1 + F2 = (2, −3, 1) N + (2, 9, −3) N = (4, 6, −2) N
From Newton’s second law, F = ma, where a is the required acceleration. Therefore
$a = \dfrac{{\boldsymbol F}}{m} = \dfrac12(4,\,6,\,-2)\,{\rm m\,s^{-2}} = (2,\,3,\,-1)\,{\rm m\,s^{-2}}$
Consult vector addition and Newton’s second lawin the Glossary for further information.
Question R3
Determine the angle between the vectors A = (3 i − j − 4 k) and B = (i + 2 j + k).
Answer R3
The scalar product of A and B is A ⋅ B = | A | | B | cos θ
where θ is the required angle between A and B.
Therefore$\cos\theta = \dfrac{\boldsymbol{A\,\cdot\,B}}{\lvert\,{\boldsymbol A}\,\lvert\,\lvert\,{\boldsymbol B}\,\rvert}$
Now | A | = $\sqrt{3^2+(-1)^2+(-4)^2} = \sqrt{26\os}$
and | B | = $\sqrt{1^2+2^2+1^2} = \sqrt{6\os}$
The scalar product A ⋅ B is given by
A ⋅ B = AxBx + AyBy + AzBz = 3 − 2 − 4 = −3
Therefore$\cos\theta = \dfrac{-3}{\sqrt{26\os}\sqrt{6\os}} \approx -0.240$
and soθ = arccos(−0.240) ≈ 104°
Consult scalar product in the Glossary for further information.
Question R4
A stationary particle with an electric charge of 3.0 × 10−6 C experiences an electric force of 1.0 × 10−3 (6, −3, 4.5) N. Determine the electric field responsible for the electric force.
Answer R4
The electric field, E = F/q where F is the electric force on a charge q. Therefore
${\boldsymbol E} = \dfrac{1.0\times 10^{-3}}{3.0\times 10^{-6}}(6,\,-3,\,4.5)\,{\rm N\,C^{-1}} = 1.0\times 10^3(2,\,-1,\,1.5)\,{\rm N\,C^{-1}}$
Consult electric field in the Glossary for further information.
2 The vector product of vectors
2.1 Introduction
We can manipulate vector expressions much as we do ordinary algebraic expressions; however some of the rules are different, and the resulting topic is known as vector algebra. In this module we assume that you are familiar with addition and subtraction of vectors, multiplication of a vector by a scalar, and the combination of two vectors to obtain a scalar product (or dot product)
It is important that you appreciate that the scalar product of two vectors, for example, (1, −2, 3) ⋅ (2, 2, 3) = 2 − 4 + 9 = 7, gives rise to a scalar quantity. We now extend the scope of vector algebra by introducing the vector product (or cross product); so called because the operation yields a vector quantity. Many equations involving vector quantities can be expressed in a convenient mathematical form in terms of the vector product.
2.2 Definition of the vector product
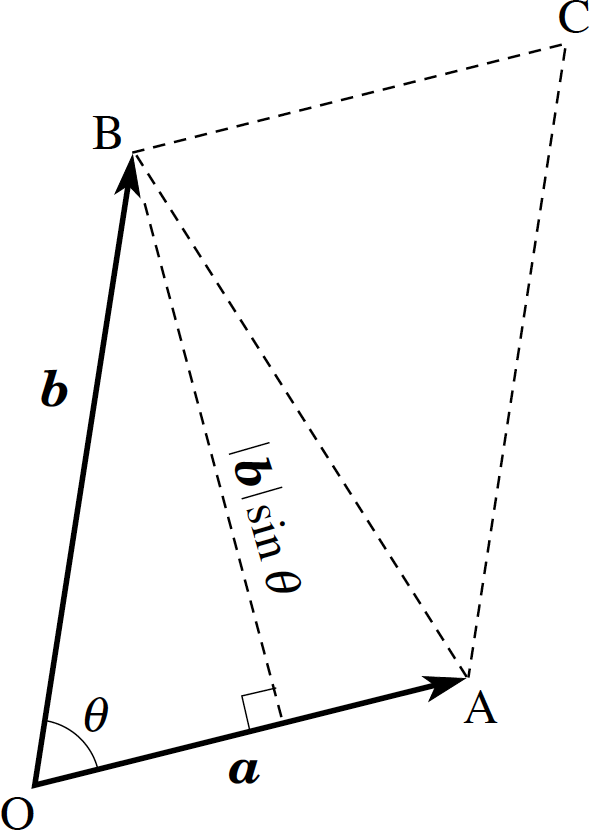
Figure 2 Area of a parallelogram.
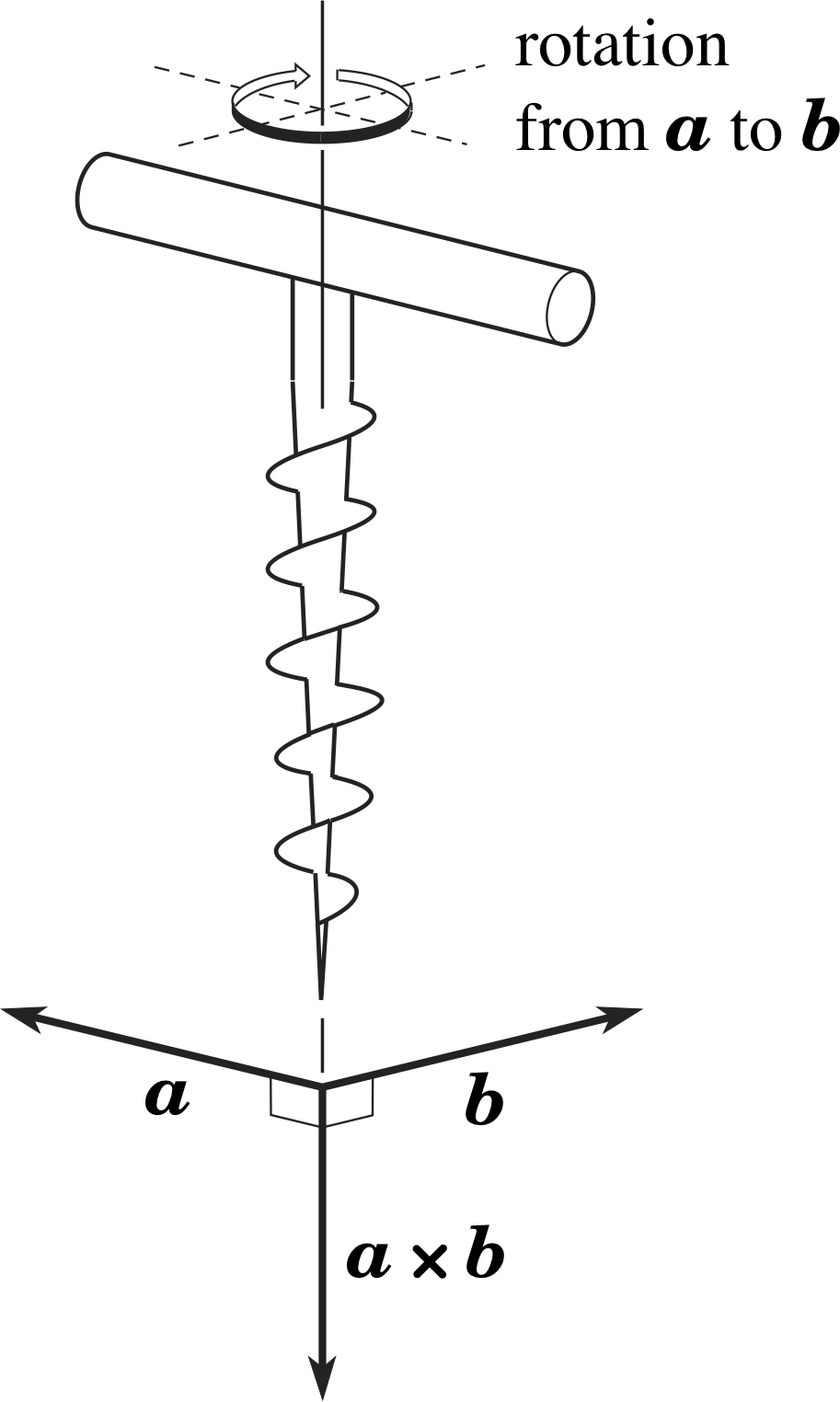
Figure 1 The right–hand screw rule.
The vector product (or cross product ) of two vectors a and b is denoted by a × b (pronounced ‘a cross b’) and is defined by
a × b = | a | | b | sin_θ n^(1)
where θ (with 0 ≤ θ ≤ π) is the angle between the two vectors, and n^ is a unit vector perpendicular to both a and b. Generally there are two distinct unit vectors perpendicular to both a and b and they point in opposite directions; we therefore use the so–called right–hand screw rule to distinguish between them. (This is also known as the corkscrew rule.)
We choose n^ to be in the direction of advance of a right–hand screw as a rotates towards b through the angle θ (see Figure 1). A right–hand screw is the commonly met type. In order to drive it into whatever the screw is being inserted it has to be rotated in a clockwise direction. i
From Equation 1 it is clear that the vector product is always a vector quantity. However, the magnitude of this vector quantity has a simple geometric meaning. From Figure 2 we see that the area of the parallelogram
OACB = base × height = | a | × | b | sin θ = | a × b |
Question T1
If a is a vector directed due north and b is a vector directed vertically upwards, what is the direction of a × b? What is the direction of b × a?
Answer T1
According to the right–hand screw rule, if a is directed due north and b is vertically upwards, then a × b is directed due east. Whereas b × a is directed towards the west, so that a × b ≠ b × a.
2.3 Properties of the vector product
Various properties of the vector product can be deduced from the definition given in Equation 1. First let us consider the effect of reversing the order of the vectors in the product.
From Equation 1,
$ \boldsymbol{a\,\times\,b} = \lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\sin\theta\,\hat{\boldsymbol n}$(Eqn 1)
$ \boldsymbol{b\,\times\,a} = \lvert\,{\boldsymbol b}\,\lvert\,\lvert\,{\boldsymbol a}\,\lvert\,\sin\theta\,(-\hat{\boldsymbol n}) = -\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\sin\theta\,\hat{\boldsymbol n}$
Therefore
b × a = −a × b(2)
This means that in vector algebra it is important to maintain the correct order of the vectors involved in a vector product. i
✦ Find the unit vectors perpendicular to the vectors a and b.
✧ The unit vectors perpendicular to a and b are ± n^, where n^ is as given in
Equation 1,
a × b = | a | | b | sin θ $\,\hat{\boldsymbol n}$(Eqn 1)
By rearranging Equation 1 the required vectors are obtained:
$\pm\left[\dfrac{{\boldsymbol a} \times {\boldsymbol b}}{\lvert\,{{\boldsymbol a}}\,\lvert\,\lvert\,{{\boldsymbol b}}\,\rvert}\right] = \pm\dfrac{{\boldsymbol a} \times {\boldsymbol b}}{\lvert\,{\boldsymbol a}\,{\boldsymbol \times}\,{\boldsymbol b}\,\rvert}$
Consider next the consequence of taking the vector product of a vector a with itself; that is a × a.
From the definition in Equation 1,
$ \boldsymbol{a\,\times\,b} = \lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\sin\theta\,\hat{\boldsymbol n}$(Eqn 1)
we have $ \lvert\,\boldsymbol{a\,\times\,a}\,\rvert = \lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol a}\,\lvert\,\sin\,0°\,\hat{\boldsymbol n} = 0$ (since sin 0° = 0), so that
a × a = 0(3) i
Thus the vector product of any vector with itself gives the zero vector.
Another case which is worthy of consideration is that in which the two vectors involved in the vector product are perpendicular to each other (i.e. they are orthogonal). Then
$ \lvert\,\boldsymbol{a\,\times\,b}\,\rvert = \lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\sin 90°\,\hat{\boldsymbol n} = \lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\hat{\boldsymbol n}$(4) i
(since sin 0° = 1), where the direction of n^ is given by our right–hand rule.
There are two other properties of the vector product which are useful for the algebraic manipulation of such products, but we will not go into the detailed proofs of these results. The first can be given the form:
a × (b + c) = (a × b) + (a × c)(5a) i
(b + c) × a = (b × a) + (c × a)(5b)
The second property can be expressed as:
(α a) × b = a × (α b) = α (a × b)(6)
where α is any scalar.
✦ Show that b × (−b) = 0.
✧ From Equation 6,
(α a) × b = a × (α b) = α (a × b)(Eqn 6)
we have b × (−b) = −(b × b), and from Equation 3,
a × a = 0(Eqn 3)
−(b × b) = 0
Put simply, these results tell us that we can use the rules of elementary algebra when manipulating vector products, provided we remember that a × b is not equal to b × a.
Question T2
Expand and simplify (a + b) × (a − b).
Answer T2
The distributive law (Equation 5b)
(b + c) × a = (b × a) + (c × a)(Eqn 5b)
enables us to expand the expression as follows:
(a + b) × (a − b) = a × (a − b) + b × (a − b)
Then using Equation 5a
a × (b + c) = (a × b) + (a × c)(Eqn 5a)
we can write
(a + b) × (a − b) = (a × a) + (a × −b) + (b × a) + (b × −b)
But, from Equation 3, we know that (a × a) = 0, and with Equation 6,
(α a) × b = a × (α b) = α (a × b)(Eqn 6)
we know that (b × −b) = 0, and also (a × −b) = −(a × b) = (b × a)
Therefore(a + b) × (a− b) = 2 (b × a)
2.4 Vector products in terms of unit vectors
You may have noticed that there was no mention of a coordinate system in the above discussion, but we often find it convenient to express a given vector in terms of the Cartesian unit vectors i, j and k in the directions of the x–, y– and z–axes in a right–handed Cartesian coordinate system. For example, the vectors 2 i + 3 j + 4 k and i − j − 3 k. Using this approach a general vector a can be expressed as
a = ax i + ay j + az k(7)
where (ax, ay, az) are the coordinates of the head of the vector if the tail of the vector is placed at the origin of coordinates.
✦ Use the scalar product to show that the vector −i + 2 j − k is orthogonal i to each of the vectors 2 i + 31 j + 4 k and i − j − 3 k.
✧ Two vectors, a and b say, are orthogonal if a ⋅ b = 0. We see that
(−i + 2 j − k) ⋅ (2 i + 3 j + 4 k) = −2 + 6 − 4 = 0
and(−i + 2 j−k) ⋅ (i − j − 3 k) = −1 − 2 + 3 = 0
which gives the required result.
You may well wonder how we were able to find the vector −i + 2 j − k which is orthogonal to two given vectors, and the answer is that we used the vector product. We will show you how this can be done shortly, but we must first express the vector product of any two vectors a and b in terms of Cartesian notation, and before we can do that we need to consider the outcome of taking the vector product of various pairs of the Cartesian unit vectors. We can evaluate these products by making use of Equations 3 and 4.
a × a = 0(Eqn 3)
$ \lvert\,\boldsymbol{a\,\times\,b}\,\rvert = \lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\sin 90°\,\hat{\boldsymbol n} = \lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\hat{\boldsymbol n}$(Eqn 4)
For example, consider the product i × i. From Equation 3 we know that the vector product of any vector with itself is zero. Hence:
i × i = 0
Similarly,j × j = 0 and k × k = 0, so that
$\left.\begin{align}\boldsymbol{i\,\times\,i} & = 0\\ \boldsymbol{j\,\times\,j} & = 0\\ \boldsymbol{k\,\times\,k} & = 0\end{align}\right\}$(8)
Now consider the product i × j. From Equation 4 we obtain:
i × j = 12 n^
However, when we apply the right–hand rule to determine the direction of n^, we find that n^ lies parallel to the z–axis. Therefore n^ = k, and it follows that i × j = k.
Similarly,j × k = i and k × i = j.
✦ Evaluate j × i.
✧ We could determine this vector product by using Equation 4,
a × b = | a | | b | sin 90° n^ = | a | | b | n^ in the same way as we have just done in determining i × j.
However, in Equation 2,
b × a = −a × b(Eqn 2)
we found that if we reverse the order of the two vectors in a vector product, we multiply the original result by −1.
Therefore we conclude that:
j × i = −(i × j) = −k
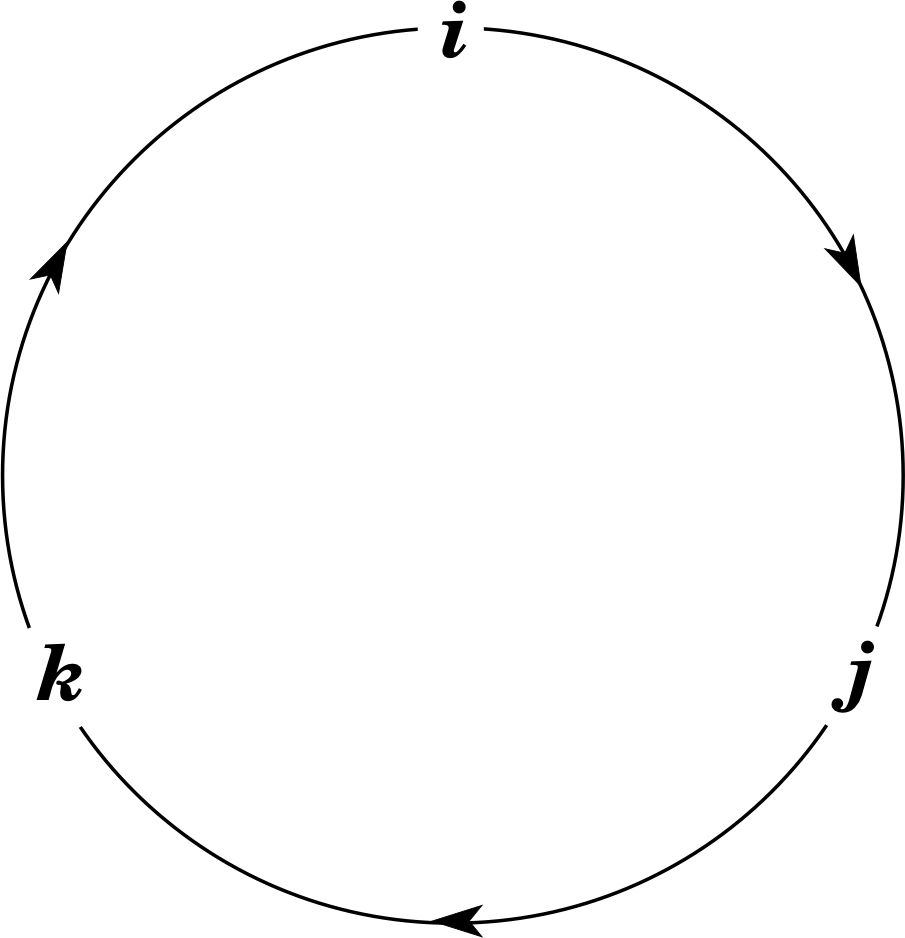
Figure 3 A memory–aid for the vector product of pairs of different Cartesian unit vectors.
If we apply similar reasoning in the determination of k × j and i × k we find k × j = −i and i × k = −j. Summarizing these results we have
$\left.\begin{align}\boldsymbol{i\,\times\,j} & = {\boldsymbol k} & ~ \boldsymbol{j\,\times\,i} & = -{\boldsymbol k}\\ \boldsymbol{j\,\times\,k} & = {\boldsymbol i} & \text{and}~~~~~~ \boldsymbol{k\,\times\,j} & = -{\boldsymbol i}\\ \boldsymbol{k\,\times\,i} & = {\boldsymbol j} & ~\boldsymbol{i\,\times\,k} & = -{\boldsymbol j}\\\end{align}\right\}$(9)
It is useful to remember the results in Equation 9, and Figure 3 should help you to do this.
If a vector product is taken between adjacent pairs of the unit vectors in the cyclic order indicated by the arrows in Figure 3, then the result is simply the third unit vector. However, if the product is taken in the anticyclic order, then the result is given by multiplying the third unit vector by −1.
We may now return to our task of evaluating the vector product of vectors a and b in terms of Cartesian notation. This product is given by
a × b = (ax i + ay j + az k) × (bx i + by j + bz k)
which may be expanded and simplified as follows:
a × b = axbx i × i + axby i × j + axbz i × k + aybx j × i + ayby j × j + aybz j × k + azbx k × i + azby k × j + azbz k × k
and using Equations 8 and 9 this becomes:
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(10) i
✦ Calculate (2 i + 3 j + 4 k ) × (i − j − 3 k)
✧ From Equation 10 i
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
(2 i + 3 j + 4 k) × (i − j − 3 k) = [3 (−3) − 4 (−1)] i + [4 (1) − 2 (−3)] j + [2 (−1) − 3 (1)] k
(2 i + 3 j + 4 k) × (i − j − 3 k) = −5i + 10 j − 5 k = 5 (−i + 2 j − k)
(This is how we were able to find the vector (−i + 2 j − k ) orthogonal to each of the vectors (2 i + 3 j + 4 k ) and (i − j − 3 k).)
✦ Find the vector product a × b of the vectors a = 2 i + j + k and b = i − j − k
Hence find the area of the triangle formed by the origin and the points A and B determined by the position vectors a and b.
✧ a × b = (1 × (−1) − 1 × (−1)) i + (1 × 1 − 2 × (−1)) j + (2 × (−1) − 1 × 1) k = 3 j − 3 k
so that| a × b | = $\sqrt{3^2+ (−3)^2} = 3\sqrt{2\os}$
The area of the triangle is therefore
$\frac12\left(3\sqrt{2\os}\right) = 3/\sqrt{2\os}$
(see Figure 2).
Question T3
Find the vector product of the two vectors a = 2 i − j + 3 k and b = i + 2 j + 2 k
Answer T3
The vector product, (a × b), may be found by applying Equation 10,
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
using the following values for the components:
ax = 2, ay = −1, az = 3; bx = 1, by = 2, bz = 2
so that
a × b = i (−2 − 6) + j (3 − 4) + k (4 + 1) = −8 i − j + 5 k
Alternatively, the answer could have been obtained from first principles by expanding (2 i − j + 3 k) × (i + 2 j + 2 k), or finally, if you are familiar with the use of determinants, by writing
${\boldsymbol {a\,\times\,b}} = \begin{vmatrix} {\boldsymbol i}& {\boldsymbol j} & {\boldsymbol k}\\a_x & a_y & a_z\\b_x & b_y & b_z\end{vmatrix} = {\boldsymbol i}\,(-2-6) - {\boldsymbol j}\,(4-3) + {\boldsymbol k}\,(4+1) = -8\,{\boldsymbol i} - {\boldsymbol j} + 5\,{\boldsymbol k}$
We can use the fact that the scalar product of two orthogonal vectors is zero to check this answer.
(−8 i − j + 5 k) ⋅ (2 i − j + 3 k) = −16 + 1 + 15 = 0
and(−8 i − j + 5 k) ⋅ (i + 2 j + 2 k) = −8 − 2 + 10 = 0
Therefore the vector product of a and b is orthogonal to both a and b.
Use the scalar product to check that your answer is indeed a vector orthogonal to both a and b.
2.5 Vector products in terms of ordered triples
A vector may be expressed in terms of an ordered triple of numbers, rather than in terms of the Cartesian unit vectors. For example:
a = (ax, ay, az)
where ax, ay and az are the scalar components of a. This means that the vector product of vectors a and b may be written as:
a × b = (ax, ay, az) × (bx, by, bz)
The vector product in terms of the Cartesian components of these vectors is given by Equation 10,
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
so that a × b = (aybz − azby, azbx − axbz, axby − aybx)(11)
Question T4
Determine the unit vectors orthogonal to vectors a and b, where a = (1, 1, 2) and b = (2, −1, 3).
Answer T4
The required unit vectors orthogonal to vectors a and b are $\pm\hat{\boldsymbol n}$, where n^ is parallel to (i.e. a multiple of) a × b. We first use Equation 11,
a × b = (aybz − azby, azbx − axbz, axby − aybx)(Eqn 11)
to find a × b where ax = 1, ay = 1, az = 2 and bx = 2, by = −1, bz = 3
Hencea × b = (3 + 2, 4 − 3, −1 − 2) = (5, 1, −3) which is a vector orthogonal to a and b, but it is not yet a unit vector. We must determine the modulus (or ‘size’) of the vector a × b by writing
| a × b | = $\sqrt{5^2+1^2+(-3)^2} = \sqrt{35\os}$
and now if we divide the vector a × b by this factor we obtain a unit vector
$\pm\hat{\boldsymbol n} = \pm\left(\dfrac{5}{\sqrt{35\os}},\,\dfrac{1}{\sqrt{35\os}},\,-\dfrac{3}{\sqrt{35\os}}\right) \approx \pm(0.845,\,0.169,\,-0.507)$
3 Triple products of vectors
Scalar and vector ‘multiplication’ of three vectors a, b, and c may yield three types of product which have sensible meanings; namely:
(a ⋅ b) c a ⋅ (b × c) and a × (b × c)
We will concentrate, in the next two subsections, on the second and third types since they involve a vector product. These are called the scalar triple product and the vector triple product since these products yield scalar and vector quantities, respectively. The first type is simple, as the following exercise illustrates; it is a scalar multiplied by a vector.
✦ Given that a = i + j, b = 2 i + k and c = i + j + k calculate (a × b) c.
✧ a × b = (i + j) × (2 i + k) = 2 so that (a × b) c = 2c = 2 i + 2 j + 2 k
3.1 The scalar triple product
As we have seen the scalar triple product is given by:
a ⋅ (b × c)(12)
✦ Does the expression (a ⋅ b) × c make sense?
✧ No, since it involves the vector product of a scalar and a vector. This means that even if we omit the brackets in Expression 12
a ⋅ (b × c)(Eqn 12)
and simply write a ⋅ b × c, it must mean a ⋅ (b × c).
✦ Given that a = i − j + 4 k, b = i + j + 2 k and c = 2 i + j + 2 k calculate
a ⋅ (b × c), b ⋅ (c × a) and c ⋅ (a × b) i
✧ b × c = 2 j − k so that a ⋅ (b × c) = (i − j + 4 k) ⋅ (2 j − k) = −6
c × a = 6 i − 6 j −3 k so that b ⋅ (c × a) = (i + j + 2 k) ⋅ (6 i − 6 j − 3 k) = −6
a × b = −6 i + 2 j + 2 k so that c ⋅ (a × b) = (2 i + j + 2 k) ⋅ (−6 i + 2 j + 2 k) = −6
The above exercise illustrates the unique identity for the scalar triple product of three given vectors
a ⋅ (b × c) = b ⋅ (c × a) = c ⋅ (a × b)(13) i
where a, b and c are arbitrary vectors. The identity can be proved as follows. Consider the value of the first term in Equation 13. Applying the expression for the vector product given in Equation 10,
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
to the product (b × c), we have
b × c = i (bycz − bzcy) + j (bzcx − bxcz) + k (bxcy − bycx)
We now take the scalar product of a with the vector (b × c) and obtain
a ⋅ (b × c) = ax(bycz − bzcy) + ay(bzcx − bxcz) + az(bxcy − bycx)
= cx(aybz − azby) + cy(azbx − axbz) + cz(axby − aybx)(14)
The first expression on the right can be transformed into the second if c replaces a, a replaces b and b replaces c.
Therefore a ⋅ (b × c) = c ⋅ (a × b)
By rearranging Equation 14 yet again, it can be shown that:
a ⋅ (b × c) = b ⋅ (c × a)
Hence the identity given by Equation 13 is proved.
Notice also that a ⋅ (b × c) = c ⋅ (a × b) and, since reversing the order does not change a scalar product:
a ⋅ (b × c) = (a × b) × c(15)
Question T5
Given a = i − j + 2 k, b = 3 i + j − k and c = −i + 2 j + k, calculate a ⋅ (b × c) and verify that this scalar triple product is equal to (a × b) ⋅ c.
Answer T5
In evaluating a × (b × c) let us first find the vector product (b × c) by applying Equation 10.
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
(b × c) = i (1 + 2) + j (1 − 3) + k (6 + 1) = 3 i −2 j + 7 k
We now take the scalar product of a with (b × c)
a × (b × c) = [(1 × 3) + (−1 × −2) + (2 × 7)] = 3 + 2 + 14 = 19
Now let us evaluate (a × b) by applying Equation 10,
(a × b) = i (1− 2) + j (6 + 1) + k (1 + 3) = −i + 7 j + 4 k
We now take the scalar product of (a × b) with c
(a × b) ⋅ c = [(−1 × −1) + (7 × 2) + (4 × 1)] = 1 + 14 + 4 = 19
Therefore we have verified that a ⋅ (b × c) = (a × b) ⋅ c for the given vectors.
3.2 The vector triple product
The vector triple product is the product given by
a × (b × c) or (a × b) × c(16)
and, as its name suggests, this triple product yields a vector quantity. The fundamental identities for the vector triple product are given by:
a × (b × c) = b (a ⋅ c) − c (a ⋅ b)(17)
and(a × b) × c = b (a ⋅ c) − a (b ⋅ c)(18) i
A useful mnemonic (memory aid) for the former identity is the so–called ‘bac cab’ rule. A glance at the right–hand side of Equation 17 should show you that the name of the rule is self-explanatory.
The identity given by Equation 17 can be proved using the Cartesian unit vector notation for vectors a, b and c. This proof is not really difficult, but it is somewhat long and tedious. However, it does give us an opportunity to practice vector algebra.
From Equation 10,
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
we can deduce that
(b × c) = i (bycz − bzcy) + j (bzcx − bxcz) + k (bxcy − bycx)
Therefore:
a × (b × c) = (ax i + ay j + az k) × [i (bycz − bzcy) + j (bzcx − bxcz) + k (bxcy − bycx)]
Using the results for the cross products of various pairs of the Cartesian unit vectors, as discussed in Subsection 2.4, we can develop this equation further, as follows:
a × (b × c) = k ax(bzcx − bxcz) − j ax (bxcy − bycx) − k ay(bycz − bzcy)
a × (b × c) + i ay(bxcy − bycx) + j az(bycz − bzcy) − i az(bzcx − bxcz)
a × (b × c) = i (aybxcy + azbxcz − aybycx − azbzcx)
a × (b × c) + j (axbycx + azbycz − axbxcy − azbzcy)
a × (b × c) + k (axbzcx + aybzcy − axbxcz −aybycz)(19)
butb (a ⋅ c) = (bx i + by j + bz k)(axcx + aycy + azcz)
andc (a ⋅ b) = (cx i + cy1 j + cz k)(axbx + ayby + azbz)
Thereforeb (a ⋅ c) − c (a ⋅ b)
= i (axbxcx + aybxcy + azbxcz − axbxcx − aybycx − azbzcx)
+ j (axbycx + aybycy + azbycz − axbxcy − aybycy − azbzcy)
+ k (axbzcx + aybzcy + azbzcz − axbxcz − aybycz − azbzcz)
= i (aybxcy + azbxcz − aybycx − azbzcx)
+ j (axbycx + azbycz − axbxcy − azbzcy)
+ k (axbzcx + aybzcy − axbxcz − aybycz)
This is the same as the right–hand side of Equation 19 and so
a × (b × c) = b (a ⋅ c) − c (a ⋅ b)
The identity given by Equation 18,
(a × b) × c = b (a ⋅ c) − a (b ⋅ c)(Eqn 18)
can be proved in a similar manner.
Question T6
Given that a = (1, −2, 3), b = (2, 1, −1) and c = (1, −1, 1) calculate a × (b × c) and verify the identity given in Equation 17,
a × (b × c) = b (a × c) − c (a × b)(Eqn 17)
Answer T6
In evaluating a × (b × c), let us first find the vector product (b × c) by applying Equation 10,
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
(b × c) = (1 − 1, −2 − 1, −2 − 1) = (0, −3, −3)
We now take the vector product of a with (b × c), again using Equation 10,
a × (b × c) = (6 + 9, 3 + 0, −3 + 0) = (15, 3, −3)
The identity in Equation 11,
a × b = (aybz − azby, azbx − axbz, axby − aybx)(Eqn 11)
is that given by the ‘bac cab’ rule:
a × (b × c) = b (a × c) − c (a × b)
The scalar product
a ⋅ c = [(1 × 1) + (−2 × −1) + (3 × 1)] = 1 + 2 + 3 = 6
The scalar product
a ⋅ b = [(1 × 2) + (−2 × 1) + (3 × −1)] = 2 − 2 − 3 = −3
Therefore b (a × c) = 6 (2, 1, −1) = (12, 6, −6), and
c (a ⋅ b) = −3 (1, −1, 1) = (−3, 3, −3)
b (a ⋅ c) − c (a × b) = (12, 6, −6) − (−3, 3, −3) = (15, 3, −3)
Hence the ‘bac cab’ identity has been verified for the given vectors.
4 The vector product in physics
There are many vector quantities in physics which may be related to pairs of other vector quantities in terms of the vector product. Some of these are beyond the level appropriate to this module, but we can consider several specific examples. i
4.1 Angular velocity
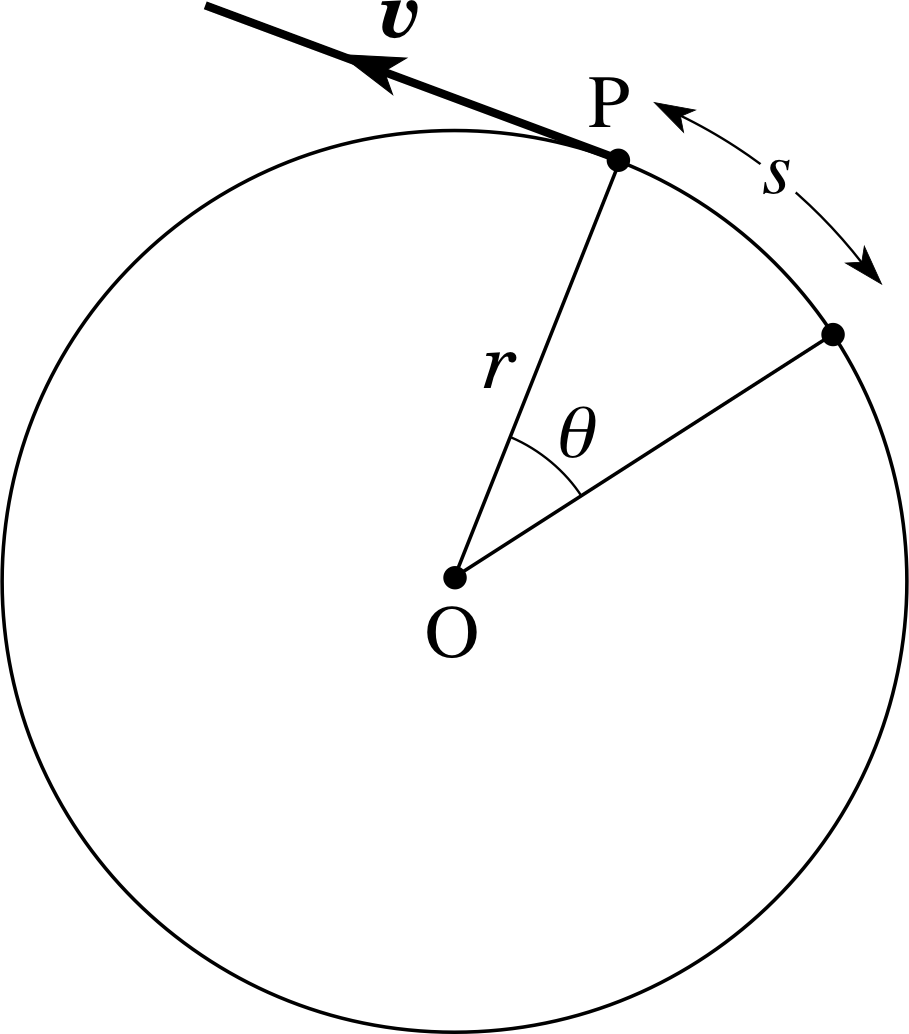
Figure 4 A particle P travels in a circular path of radius r.
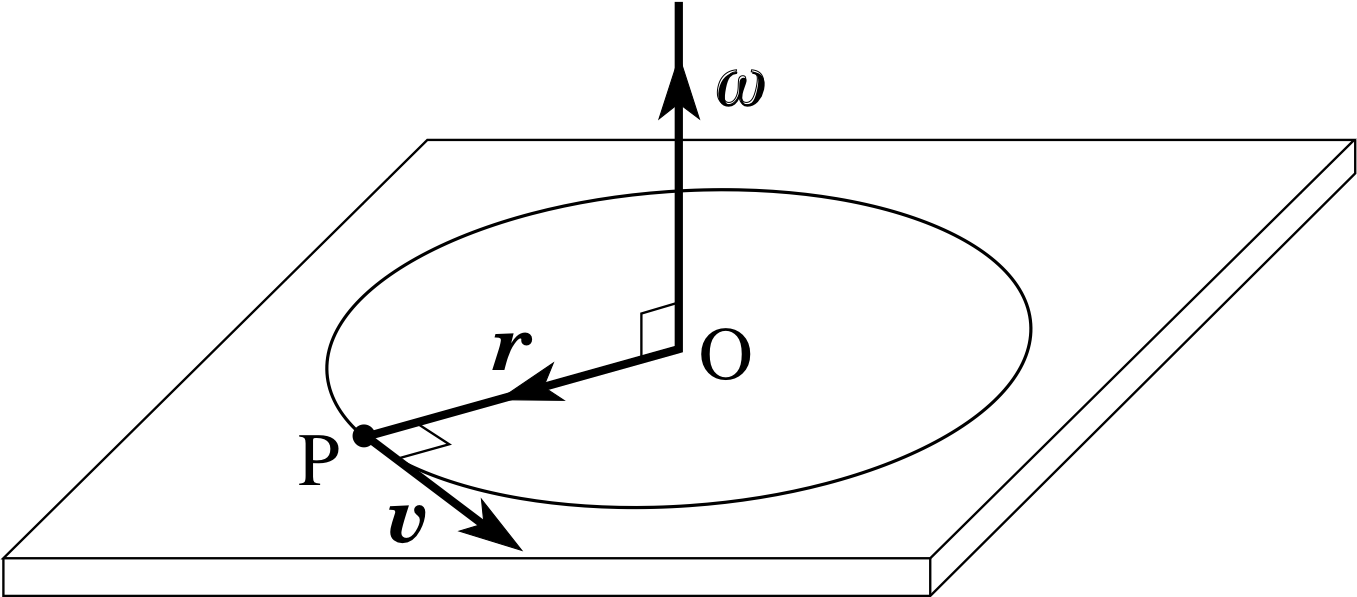
Figure 5 The direction of ω for a particle moving in a circular path.
Imagine a particle travelling in a circular path of radius r, as indicated in Figure 4. When the particle has travelled a length of arc s, the angle swept through by the radius line OP will be θ. From the definition of angle measured in radians:
$\theta = \dfrac sr$ and s = rθ
Differentiating this with respect to time, and remembering that r is constant, we obtain:
$\dfrac{ds}{dt} = r\dfrac{d\theta}{dt}$
But $\dfrac{ds}{dt}$ is the tangential speed, υ, and $\dfrac{d\theta}{dt}$ is the angular speed, ω. Therefore:
υ = rω(20)
When we take into account that the motion of the particle has direction, it is more appropriate to use a vector quantity, the tangential velocity υ, than the tangential speed, υ. In a similar way, for the angular motion, we may use angular velocity ω, rather than the angular speed, ω. But, what do we take as the direction of the angular velocity, ω? This direction is defined to be perpendicular to the plane of rotation of the particle, in the direction of advance of a right–hand screw which is rotated in the same sense as the particle is rotating. This is illustrated in Figure 5.
If we now try to relate υ and ω as we did for υ and ω in Equation 20, by simply writing υ = rω, we find that we are implying that υ and ω are in the same direction. Clearly this is incorrect and so we must find an expression which relates υ to ω in such a way that the correct relative directions of these vectors are given. The vector product provides a convenient expression which satisfies this requirement. If r is the position vector of P with respect to the centre of the circle, then υ may be given as
υ = ω × r(21) i
Question T7
Given ω = (3, −2, −1) radians s−1 and r = (1, 2, −1) m, find υ, and verify that ω and r are orthogonal (i.e. normal) to each other.
Answer T7
Given ω and r, υ can be obtained from the vector product υ = ω × r, as given in Equation 21,
by applying Equation 10.
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
Therefore
υ = (2 + 2, 3 − 1, 6 + 2) m s−2 = (4, 2, 8) m s−2
If ω and r are orthogonal their scalar product will be zero,
ω × r = (3 × 1) + (−2 × 2) + (−1 × −1) = 3 − 4 + 1 = 0
which shows that ω and r are indeed orthogonal (i.e. perpendicular) to each other.
4.2 Torque
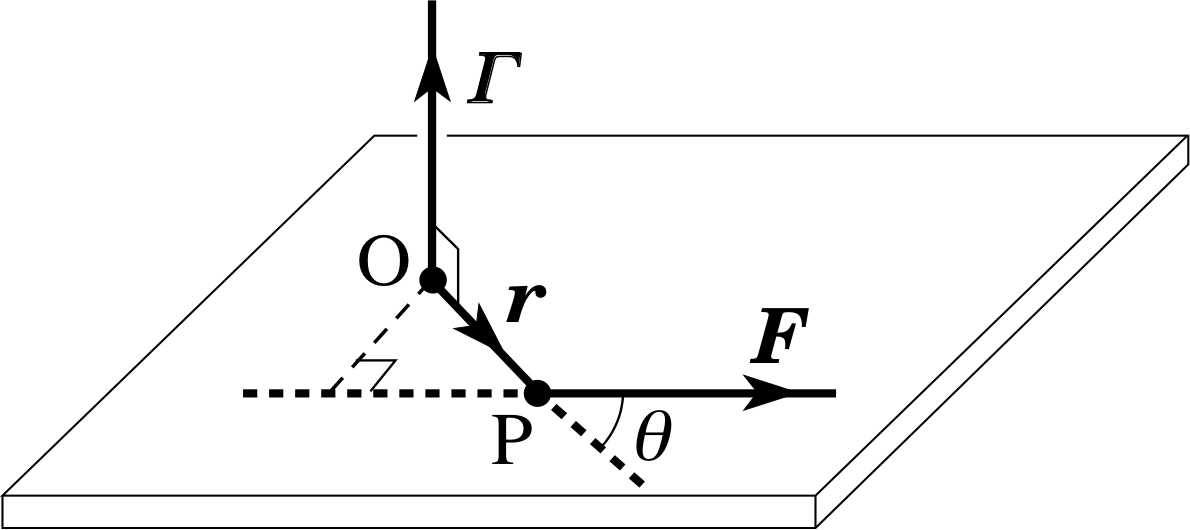
Figure 6 The torque G due to a force F acting on a particle P with position vector r relative to the point O.
We know from Newton’s laws, and our everyday experience, that a force is required to change the velocity of the centre of mass of a heavy object. For example, it takes a considerable effort to get an ocean liner moving, and an equal effort to stop it. You may not have appreciated that it also requires enormous effort to turn the ship. You may have seen a similar effect on a much smaller scale when children play on a playground roundabout. The children push it round and then jump on, and you often see a small child dragged off its feet because it has not realized how much effort is required to stop the roundabout rotating. The centre of mass of the roundabout is fixed, and the impetus of the roundabout is entirely due to its rotation.
Torque is the name given to the physical quantity that can change the angular motion of an object, and it is the angular equivalent of force. The magnitude of the torque Γ about a point O can be defined as the product of the magnitude of the force and the perpendicular distance from the point O to the line of action of the force. Alternatively, the magnitude of the torque can be regarded as the product of the (scalar) component of F perpendicular to the position vector of the particle P with respect to O, and the magnitude of the position vector. From Figure 6 both definitions can be seen to give | Γ | because:
| Γ | = | r | | F | sin θ
If we take the direction of Γ to be given by the right–hand rule, then Γ can be expressed as:
torque Γ = r × F(22)
Note that instead of the term torque, we sometimes use the term moment of a force about a point. The moment of any vector V about a point O is the vector product r × V, where r is the position vector of the point of action of V relative to O.
4.3 Angular momentum
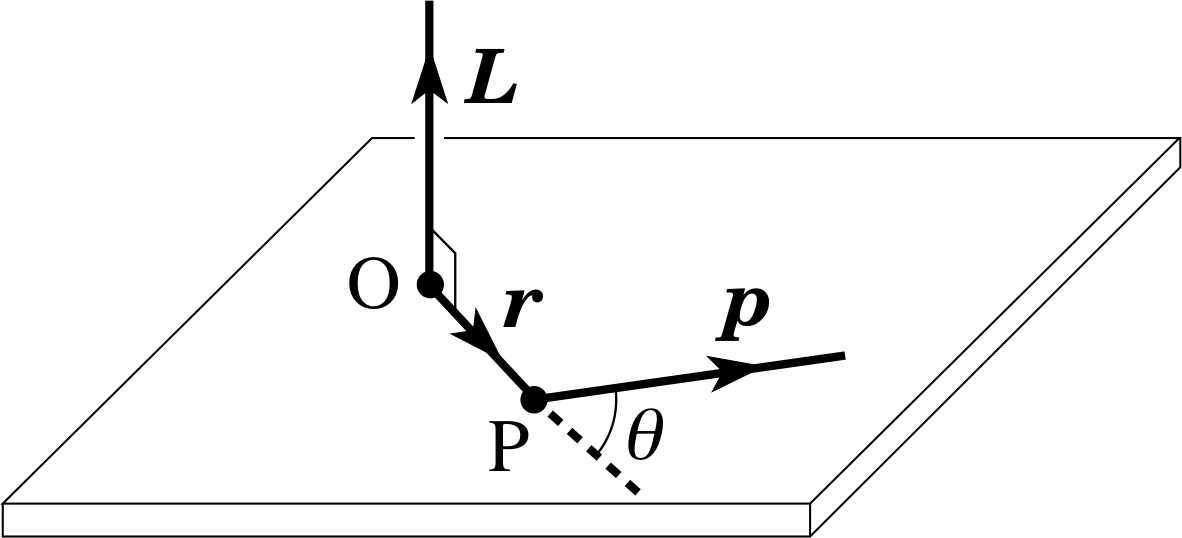
Figure 7 The angular momentum, L, of a particle P about a point O.
Force is defined as the physical quantity which can change the translational motion of a particle or body, and in this context the word ‘motion’ means linear momentum. In a similar way, torque can be regarded as the physical quantity which can change the angular momentum of a particle or body. But what do we mean by the term angular momentum? i
For a particle P of mass m moving with velocity υ, the angular momentum, L, about a point O, is the vector product of the position
vector and the linear momentum, p, where p = mυ. Therefore
angular momentum L = r × p(23)
This is illustrated in Figure 7.
✦ A particle P with position vector (i + 2 j − 3 k) m relative to the origin O has a mass of 5 kg and a velocity (2 i + j + 4 k) m s−1. Determine the magnitude of the angular momentum of P about O.
✧ Since p = 5 (2 i + j + 4 k) kg m s−1 we have
L = r × p = (i + 2 j − 3 k) ⋅ (10 i + 5 j + 20 k) kg m2 s−1 = (55 i − 50 j − 15 k) kg m2 s−1
and therefore | L | = (552 + 502 + 152)1/2 kg m2 s−1 ≈ 75.83 kg m2 s−1
Question T8
A particle P has a mass of 2 kg and a velocity (i − 2 j + 2 k) m s−1. Determine the angular momentum of P about a point O, given that the displacement vectors of P and O, from a given fixed point, are (3 i + 5 j − 6 k) m and (i + 7 j − 9 k) m, respectively.
Answer T8
The position vector r of P with respect to O is obtained by subtracting the position vector of O relative to the fixed point from the position vector of P relative to the same fixed point. Therefore:
r = [(3 i + 5 j − 6 k) − (i + 7 j − 9 k)] m = (2 i − 2 j + 3 k) m
The linear momentum p of the particle is given by mυ, where υ = (i − 2 j + 2 k) m s−2 and m = 2 kg.
The angular momentum of P about O is obtained from Equation 23,
L = r × p(23)
as follows:
L = r × p = [(2 i − 2 j + 3 k) × 2 (i − 2 j + 2 k)] kg m2 s−1
This can be evaluated using Equation 10,
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
L = 2 [i (−4 + 6) + j (3 − 4) + k (−4 + 2)] kg m2 s−1
ThereforeL = (4 i −2 j − 4 k) kg m2 s−1
If a force, F, acts on the particle, then in general, the linear momentum will change with time, but so also will the angular momentum about any fixed point. We know, from Newton’s second law, that force is equal to the rate of change of linear momentum.
A similar result holds for angular momentum; in fact
the torque of the force = the rate of change of angular momentum, and so
${\boldsymbol \Gamma} = \dfrac{d{\boldsymbol L}}{dt}$(24)
You may find it easier to remember the result in the form:
The torque acting on a particle about any point is equal to the rate of change of the angular momentum of the particle about this point, produced by the torque.
✦ A playground roundabout is in the shape of a cylinder of diameter 2 m and is free to rotate about its axis. Its mass is 500 kg and its angular momentum when it is rotating with angular speed ω is given by L = Iω k where k is a unit vector in the direction of the upward vertical and I is a constant equal to 250 kg m2. The roundabout is initially moving with an angular speed of π radians s−1, when a child of mass 15 kg tries to stop it by applying a tangential force of constant magnitude. How big must the force be in order to bring the roundabout uniformly to rest in 5 s? Do you think it possible for the child to apply such a force?
✧ Suppose that the roundabout is rotating anticlockwise when viewed from above, that r is the position vector from the axis to the point where the force is applied, and that the tangential force is F.
From Equations 22 and 24:
torque Γ = r × F(Eqn 22)
Γ = $\dfrac{d{\boldsymbol L}}{dt}$(Eqn 24)
we have
r × F = Γ = $\dfrac{d{\boldsymbol L}}{dt}$
We notice that r and F are orthogonal, and that r × F must be in the direction of −k (in order to slow the roundabout).
It follows that r × F = −rF k, where F is the magnitude of the force. However, we are told that L = Iω k, so
$\dfrac{d{\boldsymbol L}}{dt} = I\dfrac{d\omega}{dt}\,{\boldsymbol k}$
Hence, since r × F = $\dfrac{d{\boldsymbol L}}{dt}$ it follows that
$-rF =I\dfrac{d\omega}{dt}\,{\boldsymbol k}$
We are also told that the roundabout comes uniformly to rest in 5 s, from an angular speed of π rad s−1, so that
$\dfrac{d\omega}{dt} = \dfrac{-rF}{I} = \dfrac{-\pi}{5}\,{\rm rad\,s^{-1}}$
Thus
$F = \dfrac{250\,{\rm kg\,m^2}\times (\pi/5)\,{\rm rad\,s^{-1}}}{1\,{\rm m}} = 50\pi\,{\rm N} \approx 157\,{\rm N}$
This force magnitude is approximately equal to the child’s weight (its mass times g ≈ 10 m s−2, the magnitude of the acceleration due to gravity), and it seems rather unlikely that a child could apply such a force.
4.4 The Lorentz force
Electrostatic forces are observed to exist between two electric charges, regardless of whether or not the charges are in relative motion. One way of visualizing this phenomenon is to imagine that one charge produces an electric field in the space around it, and that the other charge experiences a force when it is in the region where this electric field exists.
In the same way, we may imagine that a magnetized body produces a magnetic field in the space around it. The direction of the magnetic field at a point is given by the direction of the force on the north_magnetic_polenorth–seeking pole of a small magnet placed at that point.
When a charged particle is at rest in a magnetic field, the only forces that can be exerted on it are gravitational_forcegravitational or electrostatic in origin. However, when an electric charge moves in a magnetic field, in general, an extra force comes into play which we call the magnetic force.
For a given magnetic field it may be demonstrated experimentally that the magnitude of the magnetic force depends on speed v of the particle, the magnitude | q | of its electric charge, and the angle θ between the velocity of the particle and the direction of the magnetic field. The force is found to be zero when the angle θ is zero and a maximum when θ is 90°. These observations may be summarized by writing the value of the magnetic force as:
$\displaystyle \underbrace{~~~F~~~}_{\large\color{purple}{{\text{ magnitude of force }}\atop \large{\text{ on charged particle }}}} = \underbrace{~~\lvert\,q\,\rvert~~}_{\large\color{purple}{{\text{ magnitude of }}\atop \large{\text{ the charge }}}} \underbrace{~~\upsilon~~}_{\large\color{purple}{{\text{ speed of }}\atop \large{\text{ particle }}}} \underbrace{~~B~~}_{\large\color{purple}{{\text{ magnetic }}\atop \large{\text{ field strength }}}} \underbrace{~~\sin\theta~~}_{\large\color{purple}{{\text{ sine of angle between }}\atop \large{\text{velocity and field}}}}$(25)
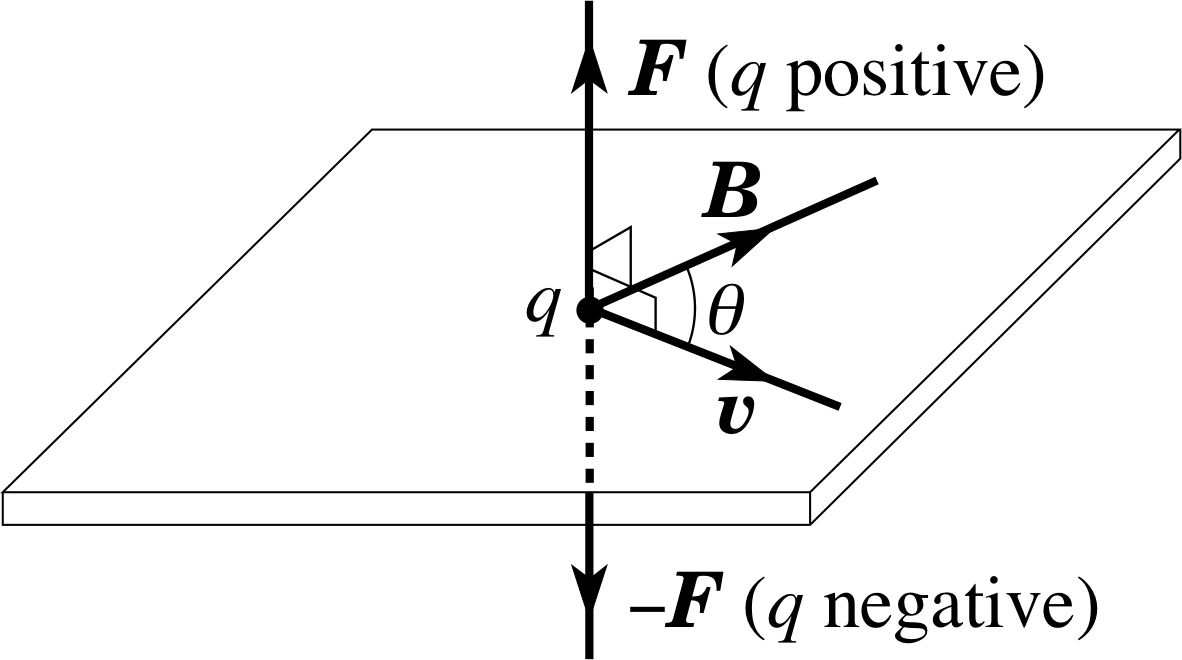
Figure 8 The direction of the magnetic force F on a charge q (±) moving with velocity υ in a magnetic field B.
The quantity B can be found at any point by measuring F, | q |, υ and θ. From this it can be shown that B may vary from point to point for a given magnetic field configuration, but that at any given point, it is the same for all charges and speeds. This demonstrates that B is a quantity which is characteristic of the magnetic field, called the magnitude of the magnetic field. The units of B may be deduced from Equation 25. In SI units they are: N C−1 m−1 s, or tesla (T).
Other experiments show that the direction of the magnetic force is normal to the plane containing the velocity vector and the direction of the magnetic field, as indicated in Figure 8. Note that the magnetic force direction for a negative charge is opposite to that for a positive charge. The magnetic field itself must be a vector quantity denoted B since it has direction.
These directional results may be summarized by writing the magnetic force in terms of the vector product:
F = q (υ × B)(26)
✦ A charged particle with charge of magnitude 5 C moves along the x–axis with a uniform velocity 3 m s−1 in a uniform magnetic field B = (0.15 j) T. What force other than that due to the magnetic field must be acting on the charge?
✧ The magnetic field is uniform (i.e. constant in both magnitude and direction) and, from
Equation 26,
F = q (υ × B)(26)
F = q (υ × B) = [5 (3 i) × (0.15 j)] N = (2.25 k) N
If the particle moves with uniform velocity, then from Newton’s laws, we know that the net force on it must be zero. In other words, a force of (−2.25 k) N must be provided in order to keep the particle moving in a straight line along the x-axis.
The above example is interesting because we see that a charged particle given an initial velocity in a uniform magnetic field, and subject to no other forces, cannot travel with uniform velocity. In fact we can be more specific.
Let us consider the type of motion that ensues if a positively charged particle is given an initial velocity υ in a uniform magnetic field B in a direction normal to B assuming that the particle has no forces acting on it other than that due to the magnetic field.
The magnetic force F on the particle of charge q and mass m is in a direction normal to both B and υ, such that F = q (υ × B). The force acts at right angles to the direction of motion of the particle, so it tends to push the particle off course, but the essential point to notice is that there is no component of force in the direction of υ, and this means that the particle will not slow down or speed up, i.e. the speed υ of the particle will be constant. Furthermore, since υ is normal to B, we see from Equation 26 that the magnitude of F will be simply | q | υ B (since sin 90° = 1).
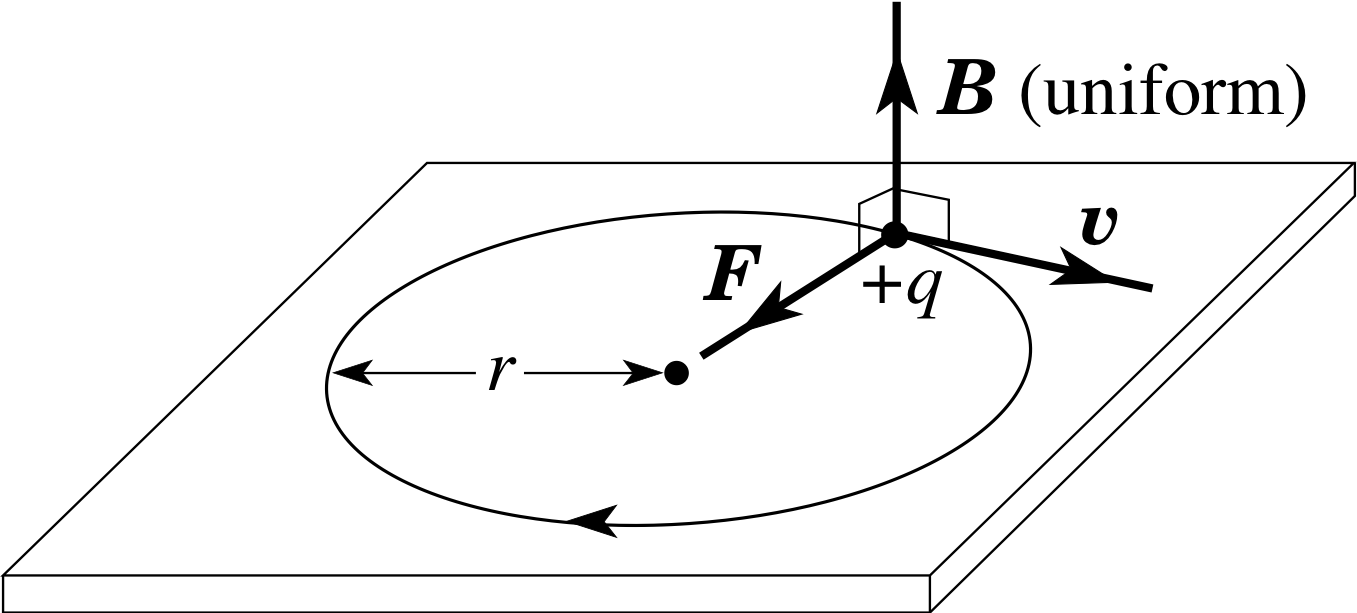
Figure 9 A positively charged particle moves in a circular path normal to a uniform magnetic field.
This means that the particle moves at constant speed υ and is subject to a force of constant magnitude that is always normal both to B and to the direction of motion of the particle. This is sufficient to ensure that the particle moves in a circular path in a plane normal to B as shown in Figure 9 for the case of a positive charge. If the charge is negative then the force will be reversed and the motion will be anticlockwise, viewed from above.
The radius r of the circular path can be deduced by applying Newton’s second law, if we use the fact that the magnitude of the acceleration towards the centre of a circle is given by υ2/r.
Therefore, assuming that the particle is of mass m, we have
m (υ2/r) = | q | υ B
and$r = \dfrac{m\upsilon}{\lvert\,q\,\lvert\,B}$(27)
When a charged particle moves in a region where both electric and magnetic fields exist, the total force on the particle is the vector sum of the electric force qE and the magnetic force qυ × B. Therefore, the total force is:
F = qE + q (υ × B)(28)
This force is known as the Lorentz force after Hendrik Lorentz, who made an important contribution to the understanding of electromagnetic phenomena. i
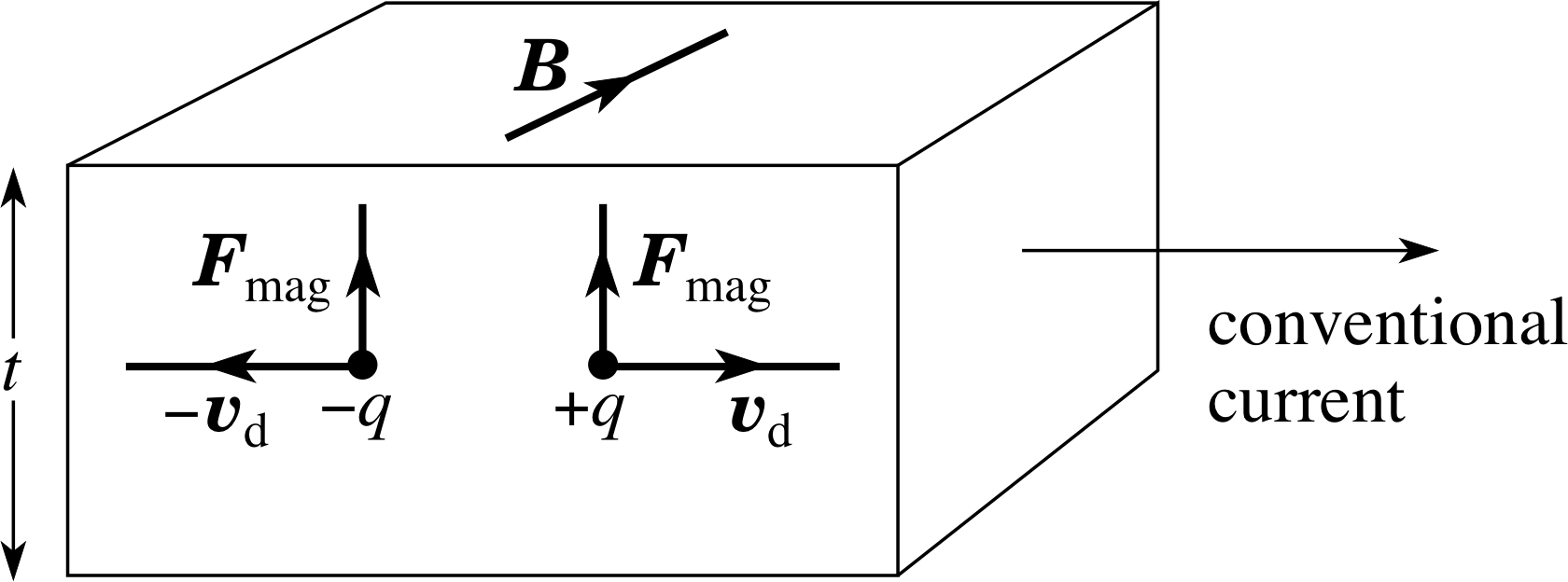
Figure 10 The magnetic force exerted on the charge carriers in a current–carrying conductor in a uniform magnetic field.
Let us now consider a situation in which both the electric and magnetic forces embodied in Equation 28 play an important role. Suppose we have a section of a uniform current–carrying conductor in a uniform magnetic field, as shown in Figure 10.
Suppose the ‘conventional’ current is carried by positive charges q moving with drift velocity υdrift in the direction of the conventional current.
According to Equation 26,
F = q (υ × B)(Eqn 26)
these charges experience a magnetic force Fmag given by
Fmag = qυdrift × B(29)
Therefore, this force is directed towards the upper face of the conductor, as shown in Figure 10. This causes the positive charges to be deflected towards the upper face, making that face become positively charged, while the bottom face has a deficiency of positive charge and so becomes negatively charged. As a result a downward electric field is created. Eventually, as the process progresses, the electric field E becomes sufficiently large that the electric force, qE, on a charge exactly balances the magnetic force q (υdrift × B). The charges subsequently drift undeflected in the direction of the current along the conductor.
The magnitude of the electric field | E |, can be related to the voltage difference VHall which arises across the thickness t between the top and bottom faces, by the equation:
$E = V_{\rm Hall}{t}$(30)
Since the electric and magnetic forces are equal:
qE = qυdrift B sin 90° = qυdrift B
Therefore: E = VHall /t = υdrift B
Hence:VHall = υdrift Bt(31)
This voltage is called the Hall voltage after E. H. Hall (1855–1938) who first investigated this effect, which is now known as the Hall effect. The effect is much larger and more easily demonstrated in a semiconductor than in a metal.
Equation 31 enables us to find the drift speed of the charge carriers, if B and t are known and VHall is measured. Furthermore, the sign of VHall tells us whether the charge carriers are positive charges moving in the direction of the conventional current, or negative charges moving in the opposite direction. You should verify for yourself that, if negative charges are involved, the magnetic force is still directed towards the upper face of the conductor. This results in an accumulation of negative charge on the top face and positive charge on the bottom face, giving the reverse polarity for the Hall voltage compared with that for positive carriers.
5 Closing items
5.1 Module summary
- 1
-
The Subsection 2.2vector product of vectors a and b is defined as
$ \boldsymbol{a\,\times\,b} = \lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\sin\theta\,\hat{\boldsymbol n}$(Eqn 1)
where θ is the angle between a and b, and n^ is a unit vector perpendicular to both a and b in the direction of advance of a right–hand screw as a rotates towards b through the angle θ.
- 2
-
The vector product is non–commutative and
b × a = −a × b(Eqn 2)
- 3
-
The vector product of a vector with itself gives the zero vector
a × a = 0(Eqn 3)
- 4
-
The vector product in Cartesian coordinate notation is given by
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
- 5
-
The vector product in ordered triple notation is given by
a × b = (aybz − azby, azbx − axbz, axby − aybx)(Eqn 11)
- 6
-
The fundamental identity for the Subsection 3.1scalar triple product is
a ⋅ (b × c) = b ⋅ (c × a) = c ⋅ (a × b)(Eqn 13)
- 7
-
The fundamental identities for the Subsection 3.2vector triple product are
a × (b × c) = b (a × c) − c (a × b)(Eqn 17)
and(a × b) × c = b (a × c) − a (b × c)(Eqn 18)
- 8
-
The vector relation between tangential and angular velocities in circular motion is
υ = ω × r(Eqn 21)
- 9
-
The Subsection 4.2torque Γ about a reference point O, due to a force F acting on a particle with position vector r relative to O is defined as
Γ = r × F(Eqn 22)
- 10
-
The Subsection 4.3angular momentum L about a point O of a particle P with linear momentum p and position vector r relative to O is defined as
L = r × p(Eqn 23)
- 11
-
The Subsection 4.2torque acting on a particle equals the rate of change of Subsection 4.3angular momentum of the particle produced by the torque. In mathematical terms
${\boldsymbol \Gamma} = \dfrac{d{\boldsymbol L}}{dt}$(Eqn 24)
- 12
-
When an electric charge q moves in a magnetic field B an extra force F arises which did not exist when the charge was at rest. This force is called a magnetic force, and is given by
F = q (υ × B)(Eqn 26)
where υ is the velocity of the charge.
- 13
-
When an electric charge q moves in a region in which both electric and magnetic fields exist, the total force is the vector sum of the electric force and the magnetic force. Mathematically
F = qE + q (υ × B)(Eqn 28)
where E is the electric field. This total force is called the Subsection 4.4Lorentz force.
- 14
-
A particle with electric charge q and mass m, given a velocity υ in a direction normal to a uniform magnetic field B, moves at constant speed υ in a circular path in a plane normal to B. The radius r of the path is
$r = \dfrac{m\upsilon}{\lvert\,q\,\lvert\,B}$(Eqn 27)
- 15
-
When a magnetic field is applied to a current–carrying conductor, in a direction normal to the electric current flow, a magnetic force is exerted on the charge carriers causing them to be deflected in a direction normal to both B and the current flow. This causes charges to accumulate on the faces of the conductor which are normal to the direction of the magnetic force. The electric field so produced causes an electric force which eventually exactly counteracts the magnetic force on a carrier, and an equilibrium condition is reached. The voltage associated with this electric field is called the Hall voltage, and its polarity enables the sign of the charges on the carriers to be determined.
5.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Define the vector product of two vectors.
- A3
-
List and explain the properties of the vector product.
- A4
-
Evaluate the vector product in terms of the Cartesian components of the vectors.
- A5
-
Recall the unique identity for the scalar triple product of vectors.
- A6
-
Recall the unique identities for the vector triple product.
- A7
-
Relate tangential velocity, angular velocity and the radial position vector using a vector product expression.
- A8
-
Define the torque acting on a particle in terms of the vector product of a position vector and the force acting on the particle.
- A9
-
Define the angular momentum of a particle in terms of the vector product of a position vector and the linear momentum of the particle.
- A10
-
Recall and use the fact that the torque acting on a particle is equal to the rate of change of angular momentum of the particle.
- A11
-
Express the magnetic force acting on a charge moving in a magnetic field in terms of the charge, the velocity of the charge and the magnetic field.
- A12
-
Give the expression for the Lorentz force acting on a charged particle which moves in a region where both electric and magnetic fields exist.
- A13
-
Show that a charged particle, given a velocity in an appropriate direction in a uniform magnetic field, will travel in a circular path. Also, derive an expression for the radius of the circular path.
- A14
-
Explain what is meant by the ‘Hall effect’, and show how this enables the signs of the charge carriers in a current–carrying conductor to be determined.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2 and A3)
Define the vector product of two vectors, and, from the definition, show that the vector product is not commutative. Explain the condition required for the vector product to give a zero vector.
Answer E1
The vector product of vectors a and b is defined in Equation 1 as
$\boldsymbol{a\,\times\,b} = \lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\sin\theta\,\hat{\boldsymbol n}$(Eqn 1)
where θ is the angle between a and b, and n^ is a unit vector normal to both a and b, in the direction of advance of a right–hand screw as a rotates towards b through the angle θ. From this definition we have
$\boldsymbol{b\,\times\,a} = \lvert\,{\boldsymbol b}\,\lvert\,\lvert\,{\boldsymbol a}\,\lvert\,\sin\theta\,(-\hat{\boldsymbol n}) = -\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\lvert\,\sin\theta\,\hat{\boldsymbol n} = -\boldsymbol{a\,\times\,b} $
Therefore the vector product is not commutative.
For the vector product to give a zero vector, assuming that neither a nor b is a zero vector, then sin θ = 0. This means that θ = 0° or 180°. Therefore, a zero vector is obtained for the vector product if the vectors a and b are in the same direction or are in opposite directions.
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E2 (A4)
Find a unit vector normal to the plane containing the vectors: (2, 2, −1) and (1, −1, 3).
Answer E2
The required unit vector is ±n^, where:
a × b = | a × b | n^, a = (2, 2, −1) and b = (1, −1, 3)
The vector product may be evaluated from Equation 10,
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
a × b = (6 − 1, −1 − 6, −2 − 2) = (5, −7, −4)
Now| a × b | = $\sqrt{\smash[b]{5^2+(-7)^2+(-4)^2}} = \sqrt{90\os}$
Therefore, the required unit vector is
$\pm\hat{\boldsymbol n} = \dfrac{(\boldsymbol{a\,\times\,b})}{\lvert\,\boldsymbol{a\,\times\,b}\,\rvert} = \pm\dfrac{1}{\sqrt{90\os}}(5,\,-7,\,-4)$
i.e.±n^ ≈ ± (0.527, −0.738, −0.422)
(Reread Subsection 2.1Subsections 2.1 and Subsection 2.52.5 if you had difficulty with this question.)
Question E3 (A4 and A5)
Given a = i + 2 j, b = j + 3 k, and c = 2 i − k, verify that a × (b × c) = (a × b) × c.
Answer E3
b × c can be evaluated using Equation 10,
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
b × c = i (−1 − 0) + j (0 + 6) + k (0 − 2) = −i + 6 j − 2 k
Therefore, given that a = i + 2 j
a ⋅ (b × c) = (1 × −1) + (2 × 6) + (0 × −2) = −1 + 12 + 0 = 11
a × b can also be evaluated using Equation 10,
a × b = i (6 − 0) + j (−3 − 0) + k (1 − 0) = 6 i − 3 j + k
Therefore, given that c = 2 i − k
(a × b) ⋅ c = (6 × 2) + (−3 × 0) + (1 × −1) = 12 + 0 − 1 = 11
Hence the identity has been verified for the vectors given.
(Reread Subsection 2.4Subsections 2.4 and Subsection 3.13.1 if you had difficulty with this question.)
Question E4 (A4 and A6)
Using the vectors given in Question E3, verify the ‘bac cab’ rule.
Answer E4
The ‘bac cab’ rule is
a ⋅ (b × c) = b (a ⋅ c) − c (a ⋅ b)(Eqn 17)
From Answer E3, we know that:
b × c = −i + 6 j − 2 k
Therefore the triple vector product can be evaluated from Equation 10,
a × b = (aybz − azby) i + (azbx − axbz) j + (axby − aybx) k(Eqn 10)
given that a = i + 2 j
a × (b × c) = i (−4 − 0) + j (2 − 0) + k (6 + 2) = −4 i + 2 j + 8 k
The scalar products (a ⋅ c) and (a ⋅ b) are
(a ⋅ c) = (1 × 2) + (2 × 0) + (0 × −1) = 2 + 0 + 0 = 2
(a ⋅ b) = (1 × 0) + (2 × 1) + (0 × 3) = 0 + 2 + 0 = 2
so that
b (a ⋅ c) = 2 (j + 3 k) = 2 j + 6 k
andc (a ⋅ b) = 2 (2 i − k) = 4 i − 2 k
which gives
b (a ⋅ c) − c (a ⋅ b) = (2 j + 6 k) − (4 i − 2 k) = − 4 i + 2 j + 8 k
Hence the ‘bac cab’ identity has been verified for the vectors given.
(Reread Subsection 2.4Subsections 2.4 and Subsection 3.23.2 if you had difficulty with this question.)
Question E5 (A6, A7 and A9)
By combining the equations υ =ω × r and L = r × p, and using the ‘bac cab’ rule, show that the angular momentum of a particle of mass m travelling in a circular path of radius r is given by L = mr2ω.
Answer E5
If L = r × p, then L = r × (mυ) = m (r × υ)
ThereforeL = m [r × (ω × r)] and using the ‘bac cab’ rule for the vector triple product
L = m [ω (r ⋅ r) − r (r ⋅ ω)]
but r ⋅ r = | r |2 = r2, and r ⋅ ω = | r | | ω | cos 90° = 0
so thatL = mr2ω
(Reread Subsection 3.2Subsections 3.2, Subsection 4.14.1 and Subsection 4.34.3 if you had difficulty with this question.)
Question E6 (A11 and A13)
A particle with charge −2.0 × 10−6 C and mass 1.5 × 10−9 kg is given a velocity of 100 (2, 1, −3) m s−1 in a uniform magnetic field of 1.0 × 10−1(1, −5, −1) T. Verify that the particle will travel in a circular path and determine the radius of the circle.
Answer E6
From Subsection 4.4 we know that circular motion will occur if the velocity and magnetic field vectors are perpendicular. If this is the case the scalar product of these vectors should be zero. Evaluating the scalar product
υ × B = 100 × 1.0 × 10−1[(2 × 1) + (1 × −5) + (−3 × −1)] T m s−1 = 10 (2 − 5 + 3) T m s−1 = 0
and we conclude that the particle will travel in a circular path. The radius of this path is given by Equation 27,
r = mυ (| q | B)(Eqn 27)
Therefore we need to find υ and B, as follows:
υ = | υ | = $100\sqrt{\smash[b]{2^2+1^2+(-3)^2}} = 100\sqrt{14\os}$ m s−1 ≈ 374 m s−1
B = | B | = 10−1$\sqrt{\smash[b]{1^2+(-5)^2+(-1)^2}}\,{\rm T} = 10^{-1}\sqrt{27\os}\,{\rm T}$ ≈ 0.520 T
Therefore$r = \dfrac{1.5 \times 10^{-9} \times 374}{2\times 10^{-6}\times 0.520}\,{\rm m} = 0.540\,{\rm m}$
(Reread Subsection 4.4 if you had difficulty with this question.)
Question E7 (A12 and A14)
Give an explanation of the Hall effect and derive an expression which enables the drift velocity of the charge carriers in a conductor to be determined from the value of the Hall voltage.

Figure 8 The direction of the magnetic force F on a charge q (±) moving with velocity υ in a magnetic field B.
Answer E7
Refer to Figure 8. If the conventional current flows in the direction shown, this may be due to positive charge carriers moving from left to right, or negative charge carriers moving from right to left. Consider carriers with positive charge q moving with drift velocity υdrift from left to right in the magnetic field B which is directed as shown. From Equation 26,
F = q (υ × B)(Eqn 26)
we know that each of these charges will experience a magnetic force given by
Fmag = q (υdrift × B)
From our right–hand screw rule we can deduce that this force will be directed upwards, towards the upper face of the conductor. This force deflects the positive charges towards the upper face of the conductor causing that face to become positively charged, while the bottom face becomes negatively charged, due to a deficiency of positive charge. This charge distribution produces an electric field and, consequently, an electric force, in a direction opposite to that of the magnetic force.
Eventually, this electric force becomes sufficiently large to exactly counteract the magnetic force, so that the charge carriers subsequently drift undeflected from left to right. As a result of the charge distribution a voltage exists between the upper and lower faces of the conductor.
If the carriers have negative charge and move from right to left, the magnetic force is in the same direction as before, since q is negative and υdrift is reversed. In this case, negative charge accumulates on the top face, and so the polarity of the voltage across the top and bottom faces is reversed. Thus, by finding the polarity of the voltage, it is possible to discover the sign of the majority of the charge carriers in the conductor. The effect described is known as the Hall effect.
If t is the distance between the top and bottom faces, and VHall is the (Hall) voltage produced, then the electric field magnitude is given by
$E = V_{\rm Hall}{t}$
When the electric and magnetic forces are equal qE = qυdriftB (since sin θ = sin 90° = 1)
so that$E = V_{\rm Hall}{t}$ = υdriftB and therefore υdrift = $V_{\rm Hall}{Bt}$
From this the drift velocity can be determined, if VHall, B and t are measured.
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.