MATH 2.6: Scalar product of vectors |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
In this module we assume that you are already familiar with addition of vectors and that you know how to multiply a vector by a scalar. i Our main purpose is to introduce the concept and use of the scalar product of vectors, which is a way of multiplying two vectors together to produce a scalar.
Imagine an aircraft landing on a runway; as it touches down, the forward components_of_a_vectorcomponent of its velocity may be quite large (perhaps something well in excess of 100 mph), but the pilot’s main concern is to keep the vertical component of the velocity small. Similarly, there are many applications of physics where it is a particular component of a vector that is of greatest concern. As a trivial illustration, when a child slides down a chute in the playground he or she is moving under the influence of gravity; it is the component of the gravitational force (i.e. the child’s weight) along the line of the chute that determines how fast the child moves. To find the kinetic energy gained in the descent we need to multiply this component by the vertical component of the displacement. The natural way to deal with components of vectors is to use the mathematical device that we introduce here – the scalar product.
In Section 2 of this module we define the scalar (or dot) product and then deduce some of its elementary properties. The section continues by showing how the product may be expressed in terms of the Cartesian unit vector and ordered triple notations. The section ends with a discussion of the way in which scalar products may be used to find the projection of one vector on to another, the component of a vector in a given direction and the angle between two known vectors.
This module also introduces the idea of a vector field. You have probably seen a simple experiment in which iron filings are scattered on a piece of paper resting on a bar magnet; when you tap the paper the iron filings form into a pattern of curves. These curves show the magnetic field lineslines of ‘magnetic force’ that lead from one magnetic_polepole of the magnet to the other. Although this experiment only shows the lines of magnetic force that lie in the plane of the paper, the lines actually extend into three dimensions, and their shape is related to the shape of the magnet – they will be very different for a horse–shoe magnet, for example. These lines of force are usually taken as evidence that a magnetic field surrounds the magnet. This is the agency responsible for exerting magnetic forces on distant objects. Since this magnetic field gives rise to forces, it must itself be characterized by a magnitude and direction at each point, and is therefore an example of a vector field. In mathematical terms a vector field is perhaps most simply thought of as a function that associates a vector with each point in space. This idea of a ‘vector-valued function of position’ is very important in physics; vector fields play a fundamental role in the description of electrical and gravitational effects as well as in magnetism. In this module you will see that scalar products are as important to the description of vector fields as they are in the treatment of individual vectors.
In Section 3 we show how scalar products are related to various physical quantities such as work done, electric potential difference, power, and the flux of a vector field, using a surface integral, illustrated by Gauss’ law in electrostatics.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 4.1Module summary and the Subsection 4.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 4.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
A force F = (4, 2, −1) N acts on a body which undergoes a displacement s = (3, −2, −6) m. Find the work done by F, the projection of F on to s, and the angle between F and s.
Answer F1
The work done is F ⋅ s which becomes Fxsx + Fysy + Fzsz and therefore
work done = [(4 × 3) + (2 × −2) + (−l × −6)] J = 14 J.
The expression for the projection of F on to s is
$\dfrac{{\boldsymbol s}\,{\boldsymbol \cdot}\,{\boldsymbol F}}{\lvert\,{\boldsymbol s}\,\rvert} = \dfrac{s_xF_x+s_yF_y+s_zF_z}{\sqrt{\smash[b]{s_x^2+s_y^2+s_z^2}}}$
so the projection is
$\dfrac{14}{\sqrt{\smash[b]{3^2+(-2)^2+(-6)^2}}}\,{\rm N}$ = (14/7) N = 2 N.
The angle between F and s is $\arccos \left(\dfrac{{\boldsymbol s}\,{\boldsymbol \cdot}\,{\boldsymbol F}}{\lvert\,{\boldsymbol s}\,\lvert\,\lvert\,{\boldsymbol F}\,\rvert}\right) = \arccos \dfrac{2}{\sqrt{21\os}} = 64.1°$
Question F2
An electric charge q = 2.0 × 10−6 C undergoes a displacement s = (2 i − 3 j + k) m in an electric field E = 103(3 i + j − 5 k) N C−1. Determine the work done by the electric force.
Answer F2
The work done is q E ⋅ s. This can be written
q (Exsx + Eysy + Ezsz)
and therefore
work done = [2 × 10−6 × 103 (6 − 3 −5)] J = −4 × 10−3 J.
1.3 Ready to study?
Question R1
Given that a = i − j + 3 k, find | a | and a unit vector in the same direction as a.
Answer R1
$\lvert\,a\,\rvert = \sqrt{1^2+(-1)^2+3^2}$.
To find the required unit vector a^ we divide the vector a by its own magnitude_of_a_vector_or_vector_quantitymagnitude | a |.
Therefore a^ = (i − j + 3 k) /$\sqrt{11\os}$.
Question R2
(a) ABC is a triangle with the angle ACB = 90°, and sides AC and AB equal to 11 cm and 15 cm, respectively. Determine the angle BAC correct to one decimal place.
(b) If ABC is a triangle with the angle ACB = 90° and if AC = $\sqrt{3\os}$ and CB = 1, find the angle BAC exactly.
Answer R2
(a) Let the required angle BAC = θ. Then cos θ = AC/AB = 1 / 5 and θ = arccos(1/5) ≈ 42.8°.
(b) arctan(1/$\sqrt{3\os}$) = 30°.
Question R3
If a = i + 2 j − 3 k and b = 2 i − 5 j + 7 k, determine the vector 3 a + 2 b in Cartesian unit vector notation.
Answer R3
3a = 3 i + 60 j − 9 k and 2 b = 4 i − 10 j + 14 k so that 3 a + 2 b = 7 i − 4 j + 5 k.
Question R4
Given c = (2, −1, 3) and d = (1, 3, −4) determine the vector 4 c − d in ordered triple notation.
Answer R4
4 c = (8, −4, 12) and − d = (−1, −3, 4) so that 4 c − d = (7, −7, 16).
2 The scalar product
2.1 A review of vectors
In this module it is assumed that you are already familiar with unit vectors, modulus of a vector, vector addition and multiplication of a vector by a scalar (scaling), but to refresh your memory we list the main results for you here.
For any two vectors a and b, and any scalar α
a + b = b + a(1)
a + (b + c) = (a + b) + c(2)
α a + α b = α (a + b)(3)
If the vectors are expressed in Cartesian form a = ax i + ay j + az k and b = bx i + by j + bz k, then the Cartesian component vectors of a are ax i, ay j and az k while the Cartesian scalar components of a are ax, ay and az. i
Also
a + b = (ax + bx) i + (ay + by) j + (az + bz) k(4)
α a = α ax i + α ay j + α az k(5)
| a | = (ax2 + ay2 + az2)1/2(6)
and a unit vector a^ = a/| a |(7)
has magnitude 1 and is parallel to a.
The above list describes two fundamental operations on vectors:
- vector addition, in which two vectors are combined in order to produce a third vector, as in Equation 4;
- scaling, in which a vector is combined with a scalar to produce another vector, as in Equation 5. We now consider an operation in which two vectors are multiplied to produce a scalar. This operation is known as the scalar (or dot) product, and we will see later that it allows us to manipulate a number of useful quantities that are easily expressed in vector form. i
2.2 Definition and properties of the scalar product
In physics we use vectors to represent vector quantities such as electric fields, gravitational fields or the velocity of a fluid, each of which has a definite magnitude and direction associated with it at every point. Very often we are interested in the component of a vector in a particular direction, as for example in the case of the velocity of an aircraft as its wheels touch the runway, when the vertical component is critical. Such components can be expressed using the scalar product.
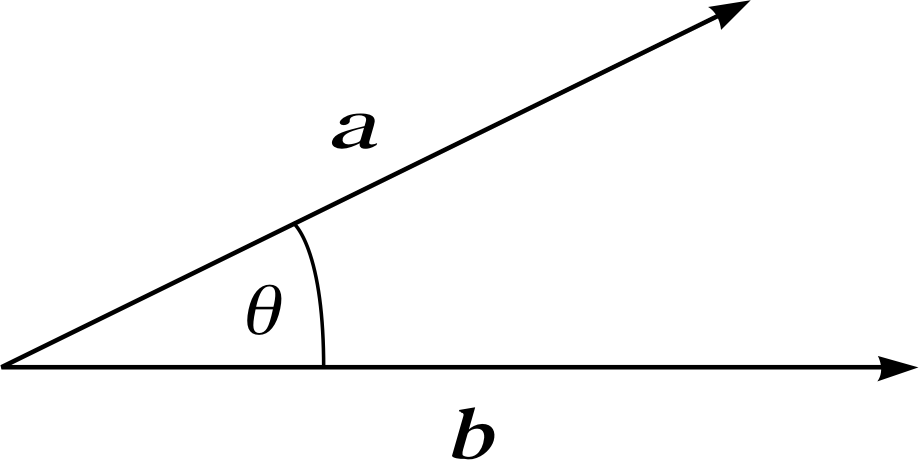
Figure 1 The angle θ between vectors a and b.
The scalar_productscalar (or dot) product of two vectors a and b is denoted by a ⋅ b (pronounced a dot b) and is defined by:
a ⋅ b = | a | | b | cos θ(8)
where θ is the angle between the two vectors (as shown in Figure 1).
More precisely, θ is defined to be the angle between the positive directions of the two vectors, such that 0 ≤ θ ≤ π.
From Equation 8 it can be seen that the scalar product is always a scalar.
Various properties of the scalar product are obvious from the definition. First, it is clear that, for any vectors a and b, we have | a | | b | cos θ = | b | | a | cos θ, and therefore the order of the vectors does not affect the scalar product, and we say that the scalar product is commutative:
commutative property a ⋅ b = b ⋅ a(9)
Consider next the outcome of taking the scalar product of a vector a with itself, i.e. a ⋅ a. From the definition (Equation 8), we have
a ⋅ a = | a | | a | cos(0°) = | a |2(10)
since cos(0°) = 1. Thus the scalar product of a vector with itself yields the square of the magnitude of the vector. Alternatively, we can express Equation 10 in the form
magnitude | a | = $\sqrt{{\boldsymbol a}\,{\boldsymbol \cdot}\,{\boldsymbol a}}$ = a(11)
where a is the magnitude or ‘length’ of the vector a. i
If the vectors a and b happen to be perpendicular (i.e. orthogonal) then the angle θ = 90° so that cos θ = 0, in which case
orthogonal vectors a ⋅ b = 0(12)
✦ The vector v represents the velocity of the air at a point just above the Earth’s surface, and at this point the vector n is normal (i.e. perpendicular) to the surface. What condition on v and n would ensure that the air is moving parallel to the surface of the Earth at the point in question?
✧ If v is parallel to the Earth’s surface then it must be orthogonal to n, and therefore v ⋅ n = 0.
In general, the scalar product is positive if 0 ≤ θ < 90° (because cos θ is positive for this range of values of θ); on the other hand, the scalar product is negative if θ is in the range 90° < θ ≤ 180° (because cos θ is negative for these values of θ).
✦ What is the angle between the vectors a = i + j and b = i? What is the value of a ⋅ b?
✧ Plotting the vectors on a sketch it is easy to see that the angle between the vectors is 45°, and therefore cos θ = 1/$\sqrt{2\os}$.
Also, $\lvert\,{\boldsymbol a}\,\rvert = \sqrt{1^2+1^2} = \sqrt{2\os}$
and | b | = 1, so that a ⋅ b = 1.
Question T1
Use a sketch of the vectors a = i + 3 j and b = j to find the angle between them. What is the value of a ⋅ b?
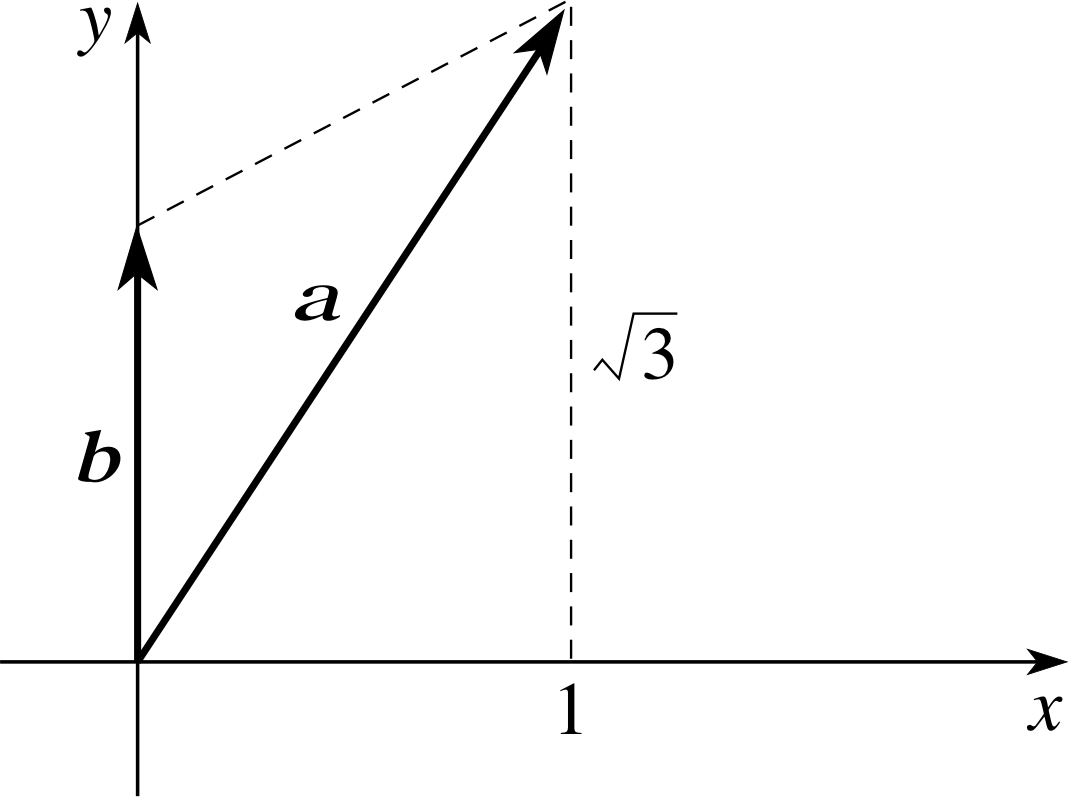
Figure 9 See Answer T1.
Answer T1
The angle between these vectors is arctan(1/$\sqrt{3\os}$) = 30°.
Since $\lvert\,{\boldsymbol a}\,\rvert = \sqrt{1^2+\left(\sqrt{3\os}\right)^2} = 2$, | b | = 1 and cos θ = $\sqrt{3\os}$/2
it follows from Equation 8,
a ⋅ b = | a | | b | cos θ(Eqn 8)
that a ⋅ b = $\sqrt{3\os}$.
✦ Show that, for arbitrary positive scalars α and β, and arbitrary vectors a and b
(α a) ⋅ (β b) = αβ (a ⋅ b)(13) i
✧ Since α a and β b are parallel to a and b, respectively, it follows that the angle between α a and β b is equal to θ, the angle between a and b. So we have (α a) ⋅ (β b) = | α a | | β b | cos θ = αβ | a | | b | cos θ = αβ (a ⋅ b).
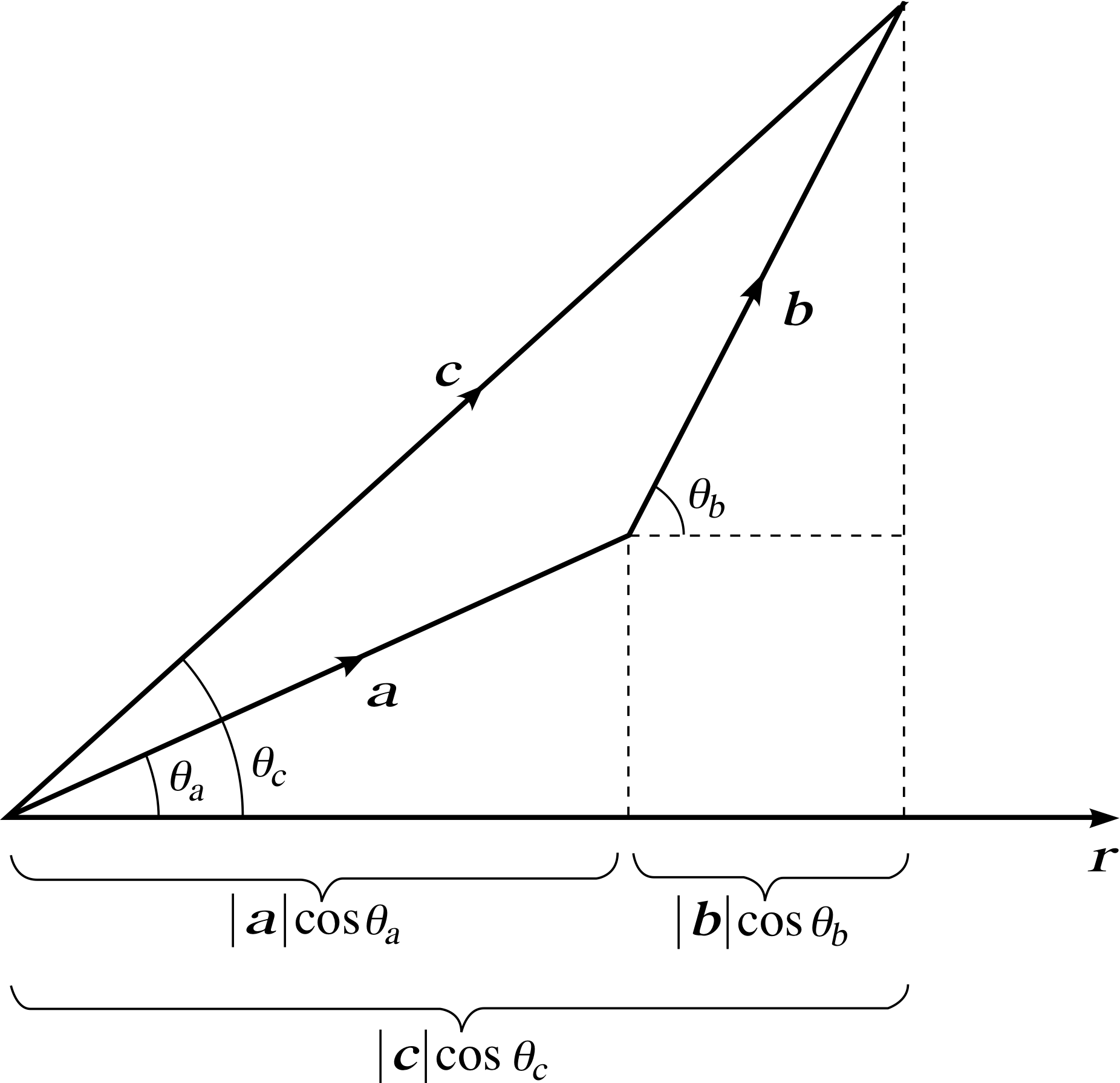
Figure 2 A property of the vector sum.
We require a further property of the scalar product, which can be easily determined from Figure 2. In this figure a, b and r are intended to represent arbitrary vectors, while c = a + b. The vectors a, b and c make angles θa, θb and θc respectively with r; it is clear from the figure that
| c | cos(θc) = | a | cos(θa) + | b | cos(θb)
Multiplying both sides of this equation by | r | we obtain
| r | | c | cos(θc) = | r | | a | cos(θa ) + | r | | b | cos(θb)
which (using Equation 8)
a ⋅ b = | a | | b | cos θ(Eqn 8)
may be rewritten in the form
r ⋅ c = r ⋅ (a + b) = r ⋅ a + r ⋅ b(14) i
We say that the scalar product is distributive over vector addition.
2.3 The scalar product in terms of unit vectors
In Equation 8 the scalar product of a and b was defined in terms of the magnitudes (i.e. the lengths) of the vectors and the angle between them – all of which are geometric concepts. The vectors can also be specified algebraically in Cartesian form
a = ax i + ay j + az k and b = bx i + by j + bz k
(with no reference to geometry), and this raises the possibility that the scalar product can also be determined in terms of the scalar components of a and b. This is indeed the case, as we shall see shortly. First we require some simple but very important results.
✦ Evaluate i ⋅ i, j ⋅ j and k ⋅ k and then evaluate i ⋅ j, j ⋅ k and k ⋅ i.
✧ From Equation 10,
a ⋅ a = | a | | a | cos(0°) = | a |2(Eqn 10)
i ⋅ i = j ⋅ j = k ⋅ k = 1 (since θ = 0)
from Equation 12,
a ⋅ b = 0(Eqn 12)
i ⋅ i = j ⋅ j = k ⋅ k = 0 (since θ = 90°).
Let us now return to our problem of evaluating the scalar product of vectors a and b in terms of the scalar components. The scalar product is given by
a ⋅ b = (ax i + ay j + az k) ⋅ (bx i + by j + bz k)
and, from Equation 14 we may expand the brackets to obtain
a ⋅ b = (ax i) ⋅ (bx i + by j + bz k) + (ay j) ⋅ (bx i + by j + bz k) + (az k ) ⋅ (bx i + by j + bz k)
Expanding the right–hand side, all terms like i ⋅ i are equal to 1, while the terms like i ⋅ j are zero, thus
a ⋅ b = ax bx + ay by + az bz(15)
✦ Evaluate the scalar product of a = i − j + k and b = −i − 3 j.
✧ a ⋅ b = (i − j + k) ⋅ (− i − 3 j + 0 k ) = (1 × −1) + (−1 × − 3) + (1 × 0) = 2.
Question T2
Evaluate the scalar product of a ⋅ b where a = 2 i − j + 3 k and b = i + 2 j + 2 k. Also evaluate | a | and | b |.
Answer T2
Given a = 2 i − j + 3 k and b = i + 2 j + 2 k, then from Equation 15,
a ⋅ b = ax bx + ay by + az bz(Eqn 15)
a ⋅ b = (2 × 1) + (−1 × 2) + (3 × 2) = 2 − 2 + 6 = 6.
From Equation 6,
| a | = (ax2 + ay2 + az2)1/2(Eqn 6)
$\lvert\,{\boldsymbol a}\,\rvert = \sqrt{\smash[b]{2^2+(-1)^2+3^2}} = \sqrt{14\os}$ and $\lvert\,{\boldsymbol b}\,\rvert = \sqrt{1^2+2^2+2^2} = \sqrt{9\os} = 3$.
2.4 Using scalar products to find angles between vectors
We now have two rather different forms for the scalar product, Equations 8 and 15, and we can take advantage of these different expressions for a ⋅ b to find the angle between the vectors a and b. i
Suppose that we wish to find the angle between the two vectors a and b of Question T2, where a = 2 i − j + 3 k and b = i + 2 j + 2 k.
First we have
a ⋅ b = | a | | b | cos θ(Eqn 8)
The left–hand side can be evaluated, using Equation 15, while on the right–hand side | a | and | b | can be evaluated using Equation 6. In Question T2 we found a ⋅ b = 6, | a | = 14 and | b | = 3, and it follows that
6 = 3 $\sqrt{14\os}$ cos θ, so that cos θ = 2/$\sqrt{14\os}$, and therefore θ ≈ 57.7°.
Notice that we have been able to determine this geometric property of the two vectors from a purely algebraic argument.
In general we have, from Equation 8,
$\cos\theta = \dfrac{{\boldsymbol a}\,{\boldsymbol \cdot}\,{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\rvert}$
so that:
$\theta = \arccos\,\left(\dfrac{{\boldsymbol a}\,{\boldsymbol \cdot}\,{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\rvert}\right)$(16) i
We may extend this further and express θ in terms of the scalar components of a and b by use of Equations 6 and 15:
| a | = (ax2 + ay2 + az2)1/2(Eqn 6)
a ⋅ b = ax bx + ay by + az bz(Eqn 15)
$\theta = \arccos\,\left[\dfrac{a_xb_x+a_yb_y+a_zb_z}{\sqrt{\left(a_x^2+a_y^2+a_z^2\right)}\sqrt{\left(b_x^2+b_y^2+b_z^2\right)}}\right]$(17)
Example 1
Determine the angles between the vector v = (1, 3, −2) and each of the three coordinate axes.
Solution
We can use the Cartesian unit vectors i, j and k to indicate the directions of the coordinate axes. To determine the angle θx between i and v we make use of Equation 17, putting a = i and b = v. Therefore, the components we require for this equation are ax = 1, ay = 0, az = 0 and bx = 1, by = 3, bz = −2
Therefore
$\theta_x = \arccos\,\left[\dfrac{1\times 1}{\sqrt{\left(1^2+0^2+0^2\right)}\sqrt{\left(1^2+3^2+(-2)^2\right)}}\right] = \arccos\,\left(\dfrac{1}{\sqrt{1+9+4\os}}\right) = \arccos\,\left(\dfrac{1}{\sqrt{14\os}}\right) \approx 74.5°$
Similarly,
$\theta_y = \arccos\,\left(\dfrac{3}{\sqrt{14\os}}\right) \approx 36.7°$ and $\theta_z = \arccos\,\left(\dfrac{-2}{\sqrt{14\os}}\right) \approx 122°$
Question T3
Determine the angle between the vectors a = (2, 1, −1) and b = (2, −3, −6).
Answer T3
The angle θ between a = (2, 1, −1) and b = (2, −3, −6) can be found using Equations 16 and 17:
$\theta = \arccos\,\left(\dfrac{{\boldsymbol a}\,{\boldsymbol \cdot}\,{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\rvert}\right)$(Eqn 16)
$\theta = \arccos\,\left[\dfrac{a_xb_x+a_yb_y+a_zb_z}{\sqrt{\left(a_x^2+a_y^2+a_z^2\right)}\sqrt{\left(b_x^2+b_y^2+b_z^2\right)}}\right]$(Eqn 17)
$\theta = \arccos\,\left[\dfrac{(2\times 2)+(1\times -3)+(-1\times -6)}{\sqrt{\left(2^2+1^2+(-1)^2\right)}\sqrt{\left(2^2+(-3)^2+(-6)^2\right)}}\right]$
$\phantom{\theta }= \arccos \dfrac{(4-3+6)}{\sqrt{6\os}\sqrt{49\os}} = \arccos \dfrac{7}{\sqrt{6\os}\times 7} = \arccos\,\left(\dfrac{1}{\sqrt{6\os}}\right)$ ≈ 65.9°
2.5 Scalar products and projections
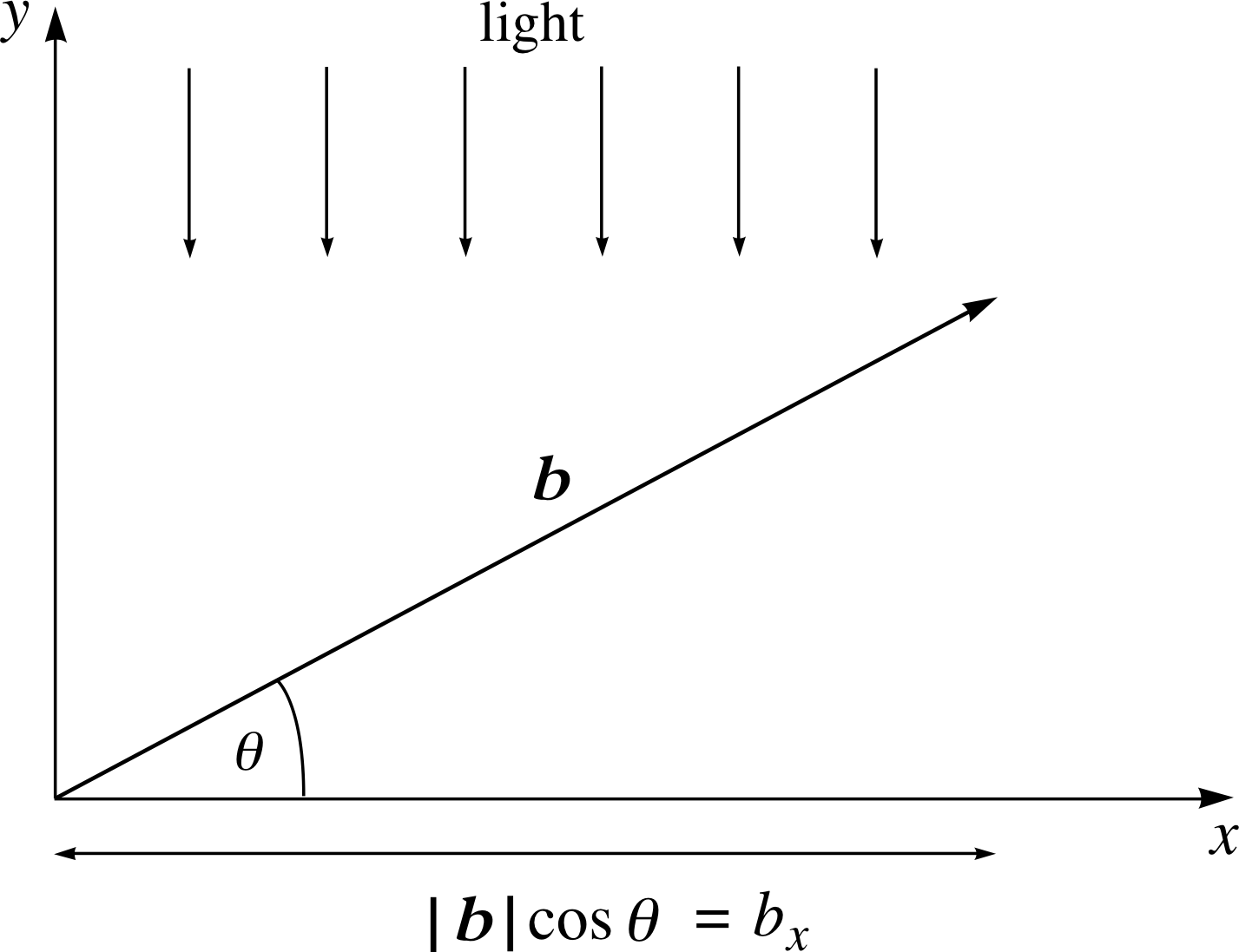
Figure 3 The projection of vector b on to the x–axis.
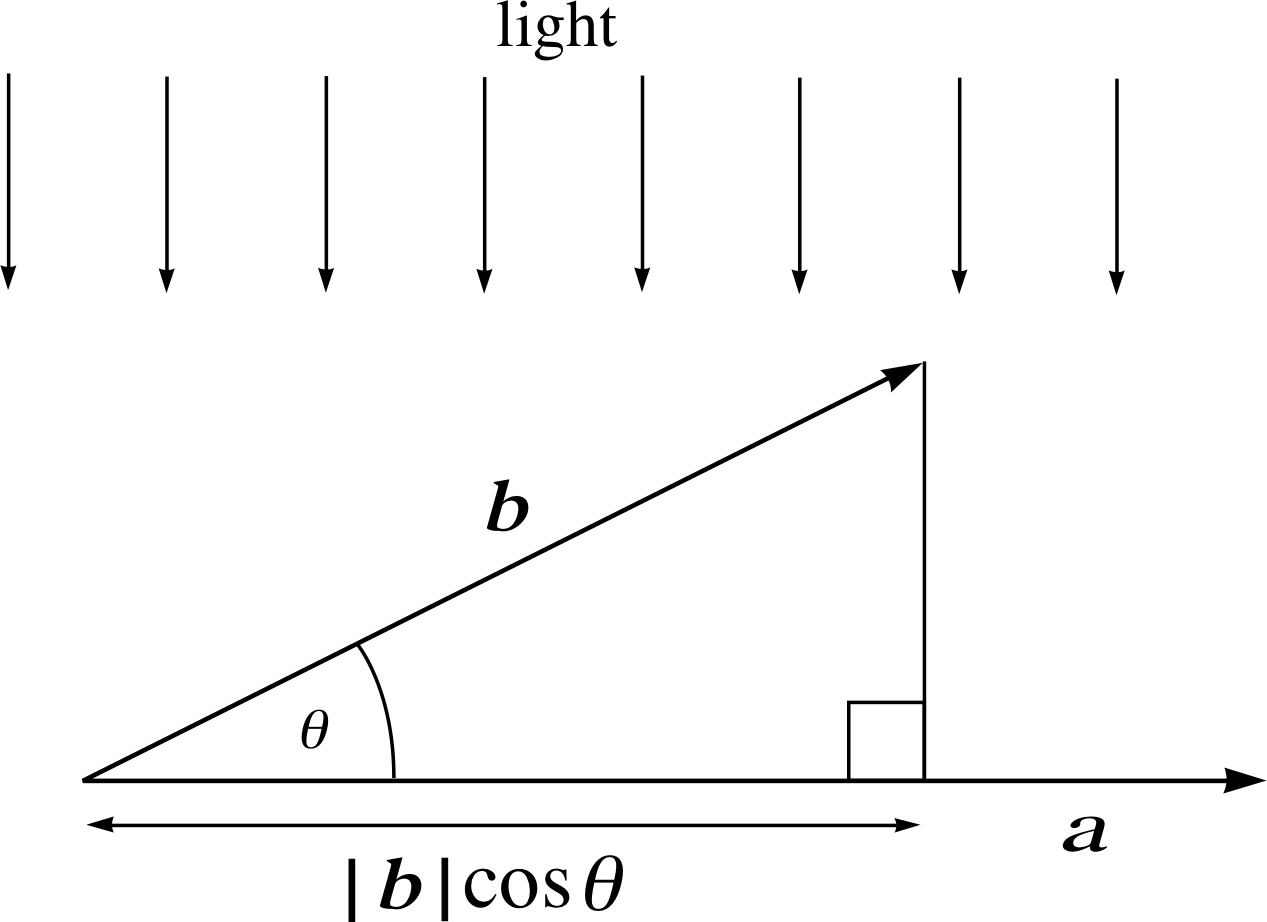
Figure 4 The projection of vector b on to vector a.
Let us now explore the relation between the scalar product of two vectors and the projection of one vector on to the other. Indeed, what is meant by the term ‘projection’ in this context? We can obtain some insight into the meaning by considering Figure 3.
Imagine parallel rayrays of light shining vertically downwards on to the x–axis. The quantity | b | cos θ which gives the size of the ‘shadow’ of vector b on the x–axis, is often termed the projection of b on to the x–axis. The projection in this case is the x–component bx, of b, so that in this context the terms projection and component are synonymous.
We can develop this idea further by considering the situation shown in Figure 4.
Here the light is imagined to be shining in a direction at right angles to vector a, casting a shadow of b on to a. The quantity | b | cos θ is the projection of b on to a. We therefore have
projection of b on to a = | b | cos θ
and multiplying both sides of this equation by | a |
| a | × projection of b on to a = | a | | b | cos θ = a ⋅ b
In words: the scalar product of vectors a and b is the magnitude of a times the projection of b on to a. Also, rearranging the equation gives
projection of b on to a = $\dfrac{{\boldsymbol a\,{\boldsymbol \cdot}\,}{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\rvert}$(18)
The projection of b on to a is sometimes known as the scalar component of b in the direction of a, or simply the components of a vectorcomponent of b in the direction of a.
In terms of the scalar components of a and b, Equation 18 becomes
projection of b on to a = $\dfrac{a_xb_x + a_yb_y + a_zb_z}{\sqrt{a_x^2+a_y^2+a_z^2}}$(19)
✦ A Cartesian coordinate system is chosen so that i, j and k are pointing East, North and vertically upward, respectively. The vector v = (20, 0.5, −1.5) m s−1 represents the velocity of a light aircraft at the moment when it lands on an airstrip. The vector n = (0.1, 0.05, 1) is normal (i.e. perpendicular) to the landing strip. What is the scalar component of the velocity perpendicular to the airstrip?
✧ The projection of v on to n = \dfrac{(0.1\times 20) + (0.05\times 0.5) + (1\times -1.5)}{\sqrt{0.1^2+(0.05)^2+1^2}}$ m s−1 ≈ 0.52 m s−1
Notice that in Equation 19 any vector in the direction of a will give precisely the same result. Moreover the vector a needs no units (since they cancel) and the dimensions of the projection of b on to a are the same as the dimensions of b.
Question T4
Determine the projection of v on to s where v = (3 i − j + 4 k) m s−1 and s = (6 i + 3 j − 2 k) m.
Answer T4
If v = (3 i − j + 4 k) m s−1 and s = (6 i + 3 i − 2 k) m, then from Equation 19,
projection of b on to a = $\dfrac{a_xb_x + a_yb_y + a_zb_z}{\sqrt{a_x^2+a_y^2+a_z^2}}$(Eqn 19)
the projection of v on to s is
$\dfrac{{\boldsymbol v\,{\boldsymbol \cdot}\,}{\boldsymbol s}}{\lvert\,{\boldsymbol s}\,\rvert} = \dfrac{(3\times 6)+(-1\times 3)+(4\times -2)}{\sqrt{6^2+3^2+(-2)}}\,{\rm{m s^{-1}}} = \dfrac{18-3-8}{\sqrt{49\os}}\,{\rm{m s^{-1}}} = \dfrac77\,{\rm{m s^{-1}}} =1\,{\rm{m s^{-1}}}$
✦ In a normal fixed wing aircraft the direction of the force exerted by the engines acts in a constant direction relative to the airframe. However the Harrier fighter has jet engines with so called ‘vector thrust’. This means that the direction of the force exerted by the engine on the airframe can be controlled by the pilot. When the Harrier is hovering, so that it is in a fixed position relative to the ground, the force exerted by the engine (the thrust) is acting vertically upwards, and it is equal in magnitude to the weight of the aircraft. Suppose that the pilot keeps the magnitude of the thrust unchanged, but changes the angle slightly so as to move forward. What happens to the height of the aircraft? Does it increase or decrease?
✧ If the aircraft is moving slowly then we can ignore the lift due to air passing over the wings. So in order to maintain the same height, the component of the thrust vector T in the vertical direction must remain constant. The projection of T on to the vertical is | T | cos θ (where θ is the angle between T and the vertical). So to stay at the same height the pilot must adjust the throttle (i.e. adjust the size of | T |) so that | T | cos θ remains constant. If the pilot changes θ from 0°, but leaves | T | fixed, then the component of T in the vertical direction will be less than the weight of the aircraft and it will begin to accelerate towards the ground.
3 Scalar products in physics
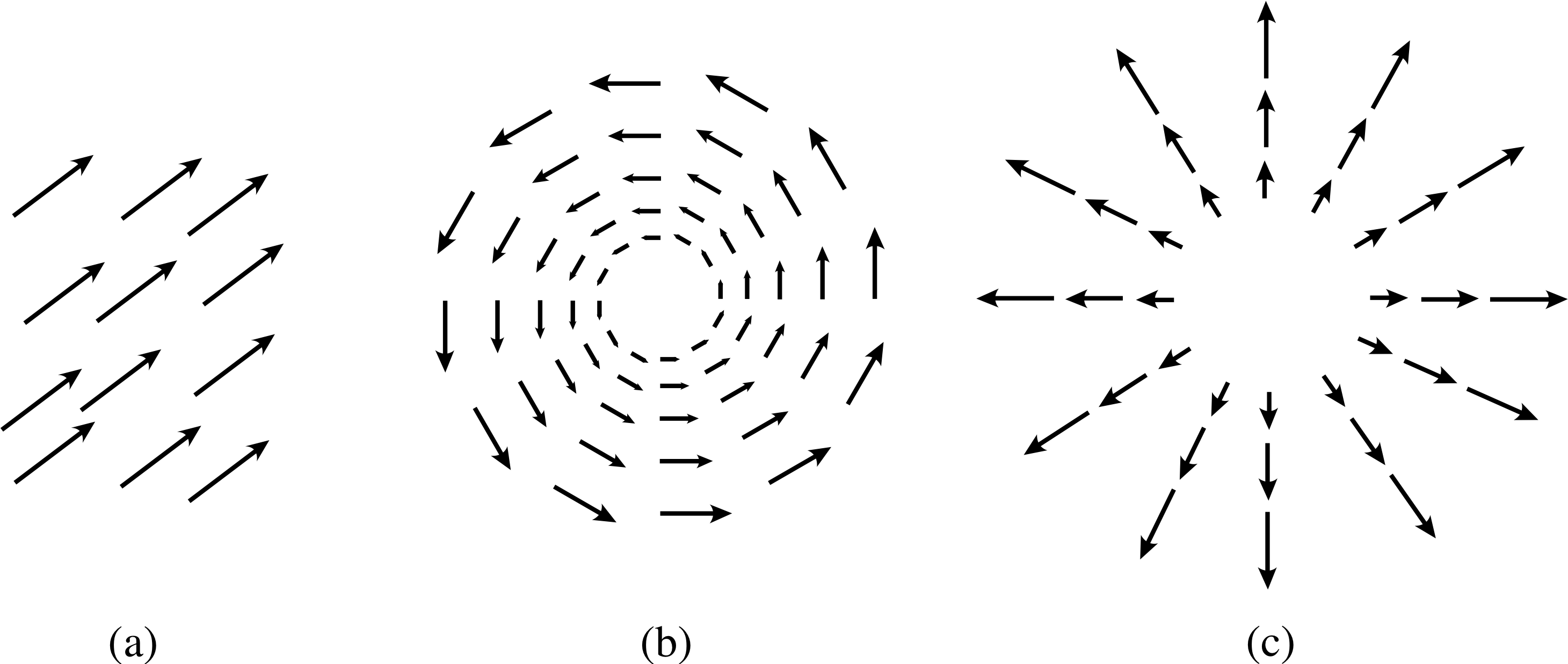
Figure 5 Some examples of vector fields. Each field is actually specified by a vector at every point throughout some region. This is impossible to show diagramatically, so the figure simply ‘indicates’ the nature of each field by showing the vectors that represent it at a finite number of points.
You may think of a vector as a mathematical object that is used to represent a specific physical quantity, such as the velocity of an object at a certain time, but in fact vectors are used in physics to model much more interesting structures. Suppose that we consider the gravitational force on a small object, of mass M say, at some point in the solar system and at some fixed instant of time (so that the planets are in fixed positions). The Sun and each of the planets will contribute to the net gravitational force on the object, but the magnitude and direction of this force will depend on the position of the object. Near to the Earth’s surface the vector that represents the force will point toward the centre of the Earth and will be of magnitude Mg, but close to the Sun it will point towards the centre of the Sun and be of much greater magnitude. i We might imagine such a vector associated with every point in the solar system, and a continuous distribution of vectors of this kind is usually known as a vector field.
Some typical examples of vector fields are indicated in Figure 5. In Figure 5a we see a uniform vector field.
When you first encounter the definition of the scalar product of two vectors a and b, you may well wonder why a ⋅ b is defined to be | a | | b | cos θ rather than | a | | b |, or | a | | b | tan θ, or something else. The choice may appear to be totally arbitrary, but in fact the form | a | | b | cos θ happens to be very useful, and it occurs frequently in mathematics and science, and particularly in the context of vector fields. Some of the more important applications of scalar products involve physical concepts beyond the scope of this module, but the following examples may convince you of the utility of the concept.
3.1 Work done by a force
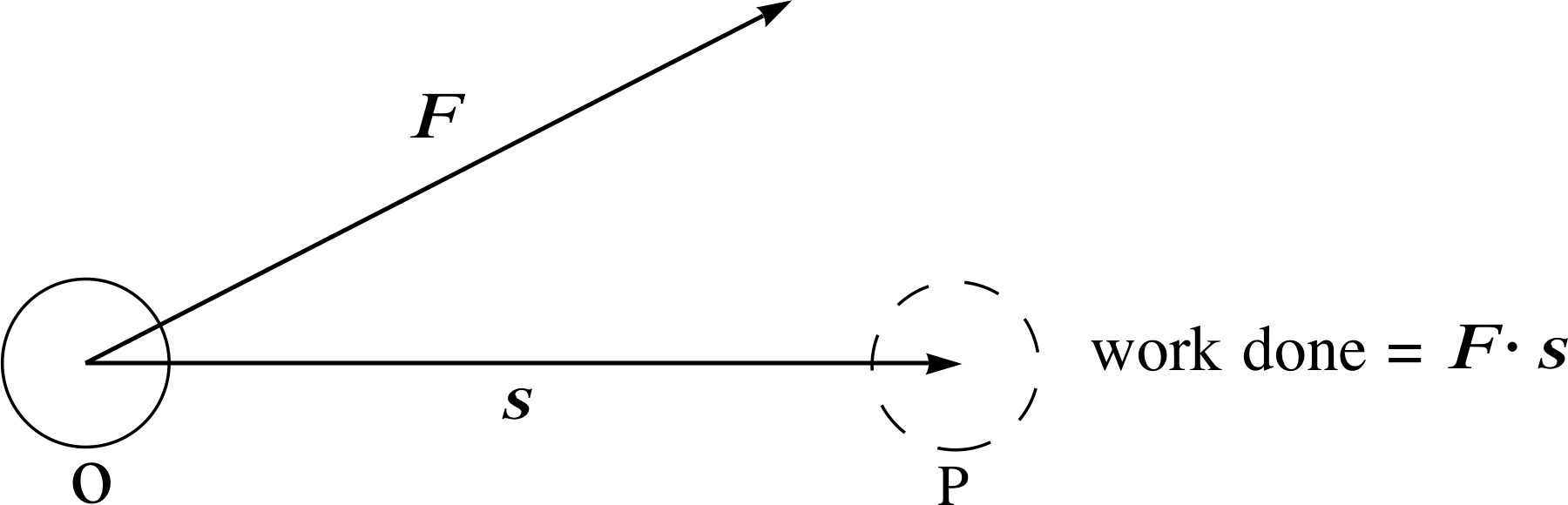
Figure 6 The work done by a constant force F on a body undergoing a linear displacement s is equal to F ⋅ s.
In physics the scalar product may be used to model mathematically the energy transferred (i.e. the work done) by a force acting on an object when the object is displaced. The simplest case involves a constant force F and a linear displacement s, as shown in Figure 6. i
The work done by F may be defined as the component of F in the direction of the displacement multiplied by the magnitude of the displacement. The scalar component of F in the direction of s is | F | cos θ, where θ is the angle between F and s. Therefore the work done by F is given by | F | | s | cos θ, which can be written as F ⋅ s. Therefore:
work done by a constant force, W = F ⋅ s(20)
which represents the amount of energy transferred from one form to another. In the SI system of units, work done, or energy, has the units of force multiplied by the units of displacement i.e. newton metre (N m). This unit is also called the joule (J).
Question T5
Find the work done by a force F = (2, −1, 3) N acting on a particle which undergoes a displacement s = (4, 2, −1) m.
Answer T5
The work done is given from Equation 20,
W = F ⋅ s(Eqn 20)
where F = (2, −1, 3) N and s = (4, 2, −1) m.
Work done = [(2 × 4) + (−1 × 2) + (3 × −1)] J = (8 − 2 − 3) J = 3 J
There are some important implications of Equation 20 to consider. If the vectors F and s are in the same direction then the angle θ is zero and cos θ = 1, so that the work done by F is given by:
work done = | F | | s | = Fs
However, if the vectors F and s are orthogonal, then θ = 90° and cos θ = 0, so that the work done by F is zero. This is a very important result. It means that if an object is undergoing a displacement in a direction perpendicular to that of a force acting on the object, then that force does no work, and no energy is transferred as a result of the action of that force. For example, if a body is travelling in a circular path as a result of a force which always acts towards the centre of the circle (a centripetal force), then this centripetal force does no work on the body.
Imagine a satellite moving around the Earth in a circular path under the influence of gravity alone. In this case the centripetal force is supplied by gravity, and since the direction of motion is perpendicular to this force, the force of gravity does no work – there is no transfer of energy – and the speed of the satellite does not change.
On the other hand, suppose that the path of the satellite is elliptical, so that its velocity may have a component directed towards (or away from the Earth), then the scalar product of the force vector with a small displacement vector is no longer zero – the force of gravity does some work i.e. there is a transfer of energy – and the speed of the satellite changes. i
Finally, let us examine the consequence on the scalar product of taking a value of θ in the range 90° < θ ≤ 180°.
In this range cos θ is negative and so the scalar product, and hence the work done by the force F, is negative. i
Advanced topic: In the most general case it would be necessary to evaluate the work done by a variable force F acting on a body which moves from one point A to another point B along a curved path. For example, we may wish to find the work done by the force of gravity on a satellite as it moves from point A to point B along an elliptical orbit. To do this we imagine that the path is split into a large number of very small steps called incremental displacements. Each incremental displacement, which is often denoted by ∆s, is sufficiently small that the force can be considered to be constant over that tiny step, and the work done by the force is evaluated for each of these small displacements. An approximate value of the total work done by the force is obtained by summing all these small contributions. This estimate will improve if we reduce the size of the increments still further, and in the limit as the size of the increments decreases to zero we obtain the exact value of the work done, which is given by the definite integral along the path. Such limits of sums are usually known as line integrals, and you may well encounter expressions such as
the total work done = $\displaystyle \int_{\rm A}^{\rm B} {\boldsymbol F}\,{\boldsymbol \cdot}\,d{\boldsymbol s}$
where the right–hand side is the limit of the sum that we have just described. However it is beyond the scope of this module to evaluate such integrals. i
3.2 Work done by a constant gravitational force
In the neighbourhood of a particular point on the Earth’s surface we may assume that the force on a mass M due to gravity is of constant magnitude Mg (where g is the acceleration due to gravity, and is approximately (9.8 m s−2) acting vertically downwards.
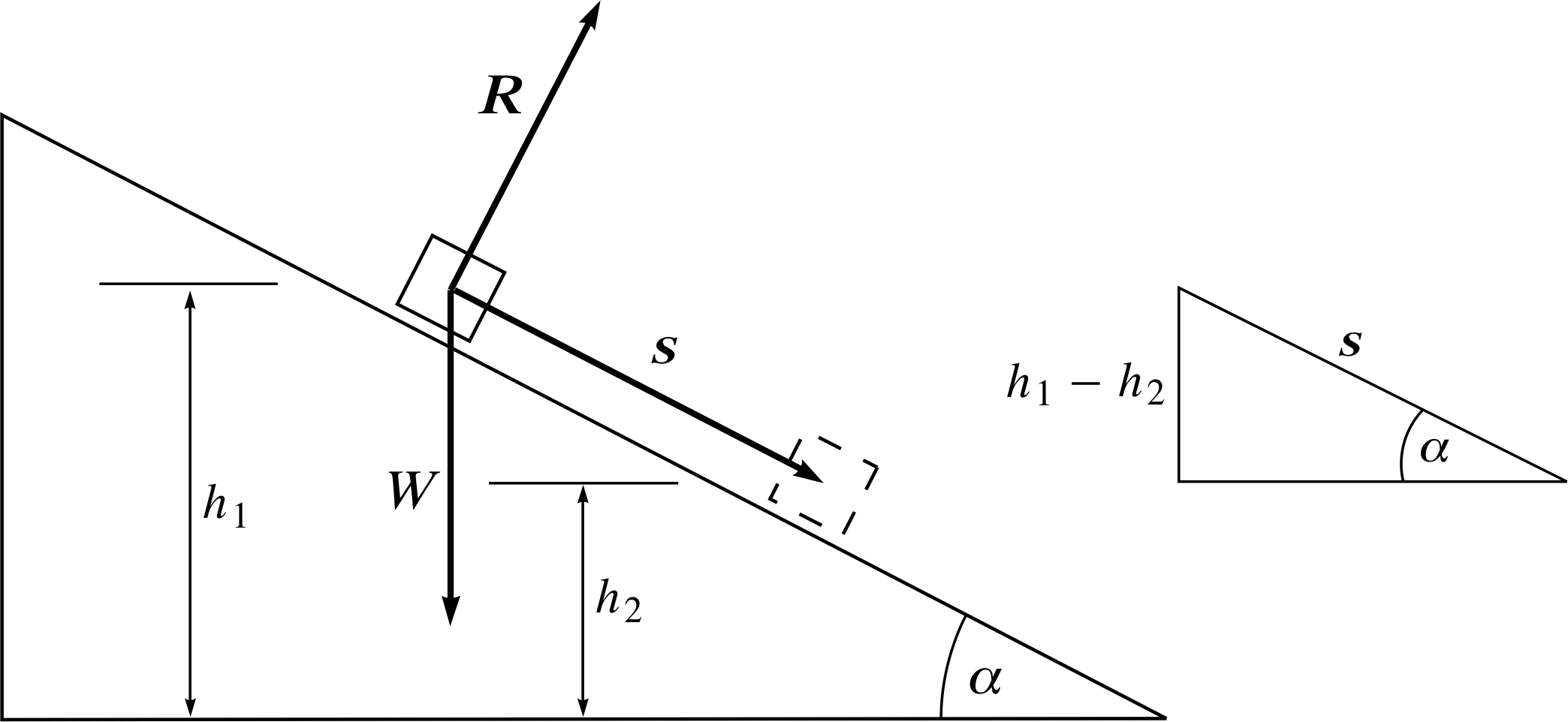
Figure 7 A block of weight W slides down a frictionless plane. The unit vector n^ which is mentioned in the text, has not been included in this diagram. It is quite easy to imagine it however, since it points in the opposite direction to W, i.e. vertically upwards
In Figure 7 a heavy block of wood slides down a frictionless plane inclined at an angle α to the horizontal. i
The normal force R, exerted on the block by the plane, does no work during the displacement since R and s are orthogonal. Consider the work done by the weight W as the block undergoes a displacement s.
The angle between W and s is (90° − α), and therefore the work done by W is given by
W ⋅ s = | W | | s | cos(90° − α) = | W | | s | sin α i
but| s | sin α = (h1 − h2) and therefore W ⋅ s = | W | (h1 − h2).
This represents the work done by W as the body is displaced such that it ‘falls’ through a vertical distance (h1 − h2). This may be thought of as the loss in gravitational potential energy of the block being compensated by an increase in kinetic energy. If n^ is a unit vector in the upward vertical direction then
W = −Mg n^
where M is the mass of the block, so that | W | = Mg and therefore the work done by the force of gravity on the block is Mg (h1 − h2).
Question T6
What is the work done by the force of gravity when a mass of 3 kg is dropped to the ground from a height of 5 m? (Remember that g ≈ 9.8 m s−2).
Answer T6
This case is equivalent to choosing α = 90° in Figure 7, and we have work done by the force of gravity is
Mg (h1 − h2) = (3 kg) × (9.8 m s−1) × (5 m) ≈ 147 J.
3.3 Work done by an electric force
We now turn our attention to the case of an electrostatic_forceelectric force, and incorporate the concept of electric field into our discussion. An electric field is said to exist at a given point if an electric charge placed at that point experiences an electric force. We may define the electric field E at any point in terms of the force F experienced by a charge q located at that point:
${\boldsymbol E} = \dfrac1q{\boldsymbol F}$
so that F = q E(21)
If E is the same at all points then the field is described as a uniform field. If the charge undergoes a linear displacement s in a uniform electric field E, then the work done by the electric force is given by:
work done = F ⋅ s = q E ⋅ s(22)
Question T7
A charge of 2 × 10−6 C undergoes a displacement s given by s = (−2 i + 6 j + 3 k) m in an electric field E = (i + 2 j − 2 k) N C−1. Find the work done by the electric force on the charge. Find also the angle between E and s.
Answer T7
From Equation 22,
work done = F ⋅ s = q E ⋅ s(Eqn 22)
the work done by the electric force when the charge q is displaced by s = (−2 i + 6 j + 3 k) m in an electric field E = (i + 2 j − 2 k) N C−1, is given by
q E ⋅ s = 2 × 10−6[(−2 × 1) + (6 × 2) + (3 × −2)] J = 2 × 10−6[−2 + 12 − 6] J = 8 × 10−2 J.
The angle between E and s can be determined using Equations 16 and 17
$\theta = \arccos\,\left(\dfrac{{\boldsymbol a}\,{\boldsymbol \cdot}\,{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\rvert}\right)$(Eqn 16)
$\theta = \arccos\,\left[\dfrac{a_xb_x+a_yb_y+a_zb_z}{\sqrt{\left(a_x^2+a_y^2+a_z^2\right)}\sqrt{\left(b_x^2+b_y^2+b_z^2\right)}}\right]$(Eqn 17)
$\theta = \arccos\,\left[\dfrac{4}{\sqrt{\left(1^2+2^2+(-2)^2\right)}\sqrt{\left((-2)^2+6^2+3^2\right)}}\right]$
$\phantom{\theta }= \arccos \dfrac{4}{\sqrt{9\os}\sqrt{49\os}} = \arccos \dfrac{4}{\sqrt{3\times 7\os}} = \arccos\,\left(\dfrac{4}{21}\right)$ ≈ 79°
Advanced topic If the electric field is not uniform, and/or the displacement is not linear, then Equation 22 (work done = F ⋅ s) has to be modified into a limit of a sum – i.e. a line integral – just as we did for motion in a gravitational field in the previous subsection. You may well encounter the work done by an electric force as a charge is displaced along any given path from point A to point B, expressed in the form
work done = $\displaystyle q \int_{\rm A}^{\rm B} {\boldsymbol E}\,{\boldsymbol \cdot}\,d{\boldsymbol s}$
An electric field is said to be conservative since the work done when a charge moves around a closed path is zero. The symbol $\oint$ is sometimes used to indicate that a line integral should be performed over a closed path. The condition that E should be conservative may therefore be written as $q \oint {\boldsymbol E}\,{\boldsymbol \cdot}\,d{\boldsymbol s}$, for every closed path. If you fix two particular points A and B, it turns out that the work done by the electric field when the charge moves from A to B doesn’t depend on the particular route followed by the charge. For a unit positive charge (q = +1 C) the negative of this work done is known as the electric potential difference between the points A and B, and often written as VB − VA. The SI unit of electric potential is called the volt (V), for convenience, rather than the newton metre per coulomb.
Example 2
Find the potential difference VB − VA between points A and B in a uniform field given by E = (2, −2, 3) N C−1, if the displacement from A to B is given by s = (1, 4, −2) m.
Solution
If E is uniform then we may use Equation 22 to obtain:
{work done by the electric force when a unit charge is moved from A to B} = E ⋅ s
= (2, −2, 3) ⋅ (1, 4, −2) N m C−1 = (2 − 8 − 6) N m C−1 = −12 N m C−1.
However VB − VA = − E ⋅ s = 12 N m C−1 = 12 V. i
3.4 Power
If you lift a heavy object then you do work, and in fact you do the same amount of work whether you lift it quickly or slowly. The difference is that you need more power to lift it rapidly than to lift it slowly. The concept of power is closely related to the work done by a force, and power is defined as the rate of doing work (i.e. the rate of transferring energy).
The SI unit of power is the joule per second (J s−1), also called the watt (W). i
In assessing the performance of a machine in doing work, the rate at which work is done is a more important parameter than the total work done by the force provided by the machine.
We consider a situation where an object is being moved by a machine, so that the velocity v of the object is some function of time. Suppose that at some particular time the machine exerts a force F on the object and causes a displacement ∆s in a time interval ∆t, then the work done by F in this time interval is given by
∆W = F ⋅ ∆s
The average power delivered by the force F over this time interval is given by
$\langle P\rangle = \dfrac{\text{work done}}{\text{time taken}} = \dfrac{\Delta W}{\Delta t} = \dfrac{{\boldsymbol F}\,{\boldsymbol \cdot}\,\Delta{\boldsymbol s}}{\Delta t} = {\boldsymbol F}\,{\boldsymbol \cdot}\,\dfrac{\Delta{\boldsymbol s}}{\Delta t}$
As the time interval ∆t tends to zero, the magnitude of the displacement ∆s also tends to zero, and the expression $\dfrac{\Delta{\boldsymbol s}}{\Delta t}$ tends to the velocity v so that
the instantaneous power P = F ⋅ v(23)
Question T8
Find the instantaneous power associated with a force F = (1, 4, −3) N acting on a body moving with velocity v = (2, 3, 3) m s−1.
Answer T8
From Equation 23,
P = F ⋅ v(Eqn 23)
the instantaneous power where F = (1, 4, −3) N and v = (2, 3, 3) m s−1 is
P = [(1 × 2) + (4 × 3) + (−3 × 3)] W = (2 + 12 − 9) W = 5 W.
3.5 Flux of a vector field across a surface
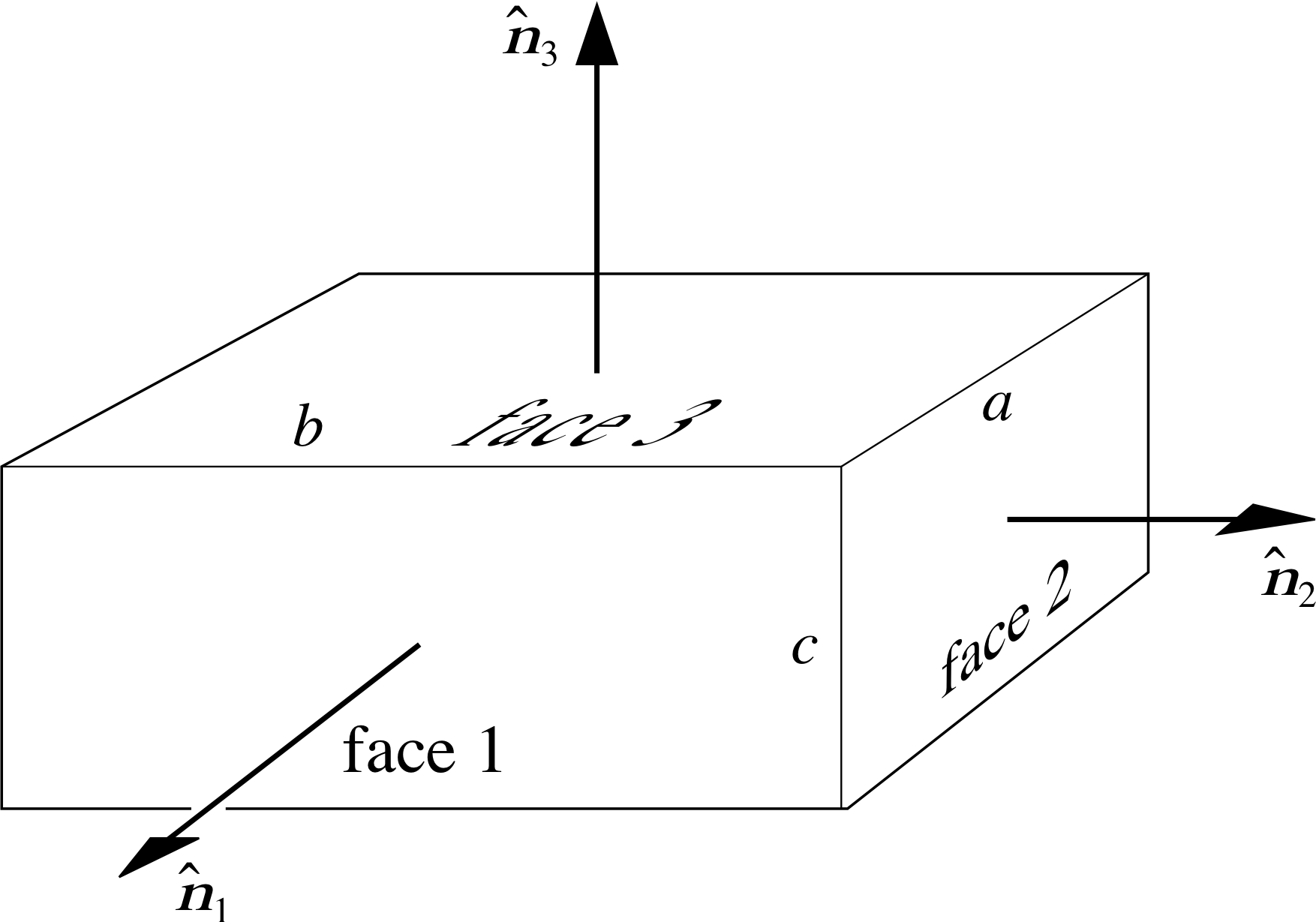
Figure 8 Unit normal vectors on the faces of a box. To avoid cluttering up the diagram the S vectors have been left out and only the n^ vectors have been drawn.
Most of the vector quantities that we encounter in physics have magnitudes and directions that have intuitive links to their physical nature. For example, it is natural to choose an arrow to describe a velocity, since we get a sense of an object moving faster in a particular direction as the length of the arrow increases. However, there are some physical quantities for which vectors do not immediately come to mind, but these quantities can be associated with a magnitude and a direction. The area of a surface is such a quantity.
Figure 8 shows the outward pointing unit normal vectors on three faces of a rectangular box, so that, for example, the unit vector n^1 is associated with face 1 of area bc. The vector S1 = bc n^1 encapsulates two important pieces of information about face 1 of the box: its area and the orientation of the surface. Similarly we can construct vectors S2 = ca n^2 and S3 = ab n^3 to represent the areas of faces 2 and 3 of the box.
For convenience we will now suppose that the unit normal vectors are in the directions of the Cartesian coordinate axes, so that n^1 = i, n^2 = j, n^3 = k. Now imagine that the box is just a cage, and that the edges are made of wire. The cage is now immersed in a stream of water that flows uniformly along the y–axis (i.e. in the direction of n^2 in Figure 8). How much water flows across the three faces in one second? Clearly the water is travelling parallel to faces 1 and 3, so no water crosses them; the amount of water crossing face 2 will depend on its area and the velocity of the stream. If the velocity of the stream is v (m s−1) and the dimensions of the cage are measured in metres, then the volume of water crossing face 2 in one second will be ac | v |.
Now for a more difficult question. Suppose that the stream is no longer directed along the y–axis, but v is some arbitrary vector, what volume of water crosses face 2 in one second now?
Suppose that v = vx i + vy j + vz k then it is only the component vector vy j of the velocity that is relevant, since the remaining components are parallel to face 2. The volume of water crossing face 2 in one second is the area of the face (i.e. ac) times the magnitude of this component, which gives ac | vy |.
In general we might be given a flat surface of any shape, with area A say, perpendicular to some unit vector n^, and we wish to know the volume of liquid that crosses the area in one second. The vector S = A n^ then contains all the information we need about the area, and it is the component of v in the direction of n^ that is relevant.n^
In fact:
$\displaystyle \left\{\text{the volume of fluid that crosses} \atop \text{the surface S in one second}\right\} = \left\{\text{area of the} \atop \text{surface}\right\}\left\{\text{the component of }{\boldsymbol v}\text{ in} \atop \text{the direction of S}\right\} = \lvert\,{\boldsymbol S}\,\rvert \dfrac{{\boldsymbol S}\,{\boldsymbol \cdot}\,{\boldsymbol v}}{\lvert\,{\boldsymbol S}\,\rvert} = {\boldsymbol v}\,{\boldsymbol \cdot}\,{\boldsymbol S}$ i
In the case that we have been considering the vector field v is uniform and the surface S is flat, but more often the vector field varies from point to point and the direction of the normal changes as we move over a curved surface. Since the normal to the surface varies, it is not sensible to refer to the entire surface as a vector, so let us call it S. Although such a general case appears to be very much more difficult, we can in fact approach it in a very similar fashion. We simply divide the surface up into many small regions ∆S that are almost flat, then add up all the contributions v ⋅ ∆S from these small regions. As the size of each region shrinks our approximation improves, until in the limit (of zero area) we obtain an exact value for the volume of liquid that flows across the surface S in one second. Such a limit of a sum is known as a surface integral and is often written in the form $\int_S {\boldsymbol v}\,{\boldsymbol \cdot}\,d{\boldsymbol S}$ although you may also see the notation $\iint_S {\boldsymbol v}\,{\boldsymbol \cdot}\,d{\boldsymbol S}$ i
The surface integral $\int_S {\boldsymbol v}\,{\boldsymbol \cdot}\,d{\boldsymbol S}$ is often known as the flux_of_a_vector_fieldflux of the vector field v over the surface S, and such expressions occur in many branches of physics, but particularly in the study of electricity and magnetism, in addition to the study of fluids. Fortunately we are very rarely required to calculate such expressions; they occur most frequently in the development of the theory.
The flux of an electric field across a spherical surface
We can specify the position of a point P relative to the origin by a vector BI, and then the electric field E at r due to a point charge q placed at the origin is given by
${\boldsymbol E} = \dfrac{1}{4\pi\epsilon_0}\dfrac{q\hat{\boldsymbol r}}{r^2}$(24) i
This means, from Equation 21,
F = q E(Eqn 21)
that a point charge q1 placed at P will experience a force
${\boldsymbol F} = q_1{\boldsymbol E} = \dfrac{1}{4\pi\epsilon_0}\dfrac{q q_1 \hat{\boldsymbol r}}{{\boldsymbol r}\,{\boldsymbol \cdot}\,{\boldsymbol r}}$(25)
✦ A point charge +5 C is placed at the origin and a point charge +3 C is placed at the point r = (1, 3, 2) m.
Calculate the force F on the second charge due to the first charge.
✧ r = (1, 3, 2) m so that
| r |2 = r ⋅ r = (1, 3, 2) ⋅ (1, 3, 2) m2 = (1 + 9 + 4) m2 = 14 m2
and therefore | r |= $\sqrt{14\os}$ m
and$\hat{\boldsymbol r} = \left(\dfrac{1}{\sqrt{14\os}},\,\dfrac{3}{\sqrt{14\os}},\,\dfrac{2}{\sqrt{14\os}}\right)$
From Equation 25,
${\boldsymbol F} = q_1{\boldsymbol E} = \dfrac{1}{4\pi\epsilon_0}\dfrac{q q_1 \hat{\boldsymbol r}}{{\boldsymbol r}\,{\boldsymbol \cdot}\,{\boldsymbol r}}$(Eqn 25)
we have
${\boldsymbol F} = \dfrac{q q_1\hat{\boldsymbol r}}{4\pi\epsilon_0{\boldsymbol r}\,{\boldsymbol \cdot}\,{\boldsymbol r}} = \dfrac{5\times 3\times\left(\dfrac{1}{\sqrt{14\os}},\,\dfrac{3}{\sqrt{14\os}},\,\dfrac{2}{\sqrt{14\os}}\right)}{4\pi\epsilon_0\times 14} =\dfrac{15}{56\pi\epsilon_0\sqrt{14\os}}(1,\,3,\,2)\,{\rm N}$
Example 3
Calculate the flux of the electric field E due to a point charge q placed at the origin across a sphere of radius a with its centre at the origin.
Solution
We have to calculate the surface integral $\int_S {\boldsymbol E}\,{\boldsymbol \cdot}\,d{\boldsymbol S}$ over the surface of the sphere S. First we divide the surface into a large number of small regions, then we concentrate on one of these regions, with area ∆S. We select a point P on the surface of the sphere, lying inside the chosen region, and suppose that the position of P is defined by the vector r = a r^ say. In the case of a sphere the direction of the outward normal to the surface always points along a radius, so we have
ΔS = ΔS r^
and it follows from Equation 24 that
${\boldsymbol E}\,{\boldsymbol \cdot}\,\Delta{\boldsymbol S} = \dfrac{1}{4\pi\epsilon_0} \left(\dfrac{q\,\hat{\boldsymbol r}}{{\boldsymbol r}\,{\boldsymbol \cdot}\,{\boldsymbol r}}\right)\,{\boldsymbol \cdot}\,(\Delta{\boldsymbol S}\,\hat{\boldsymbol r}) = \dfrac{q}{4\pi\epsilon_0 a^2}\Delta S$
(since r ⋅ r = a2 and n^ ⋅ n^ = 1).
We now need to add all the contributions from all the small regions over the entire surface of the sphere. The quantity $\dfrac{q}{4\pi\epsilon_0 a^2}$ is constant on the surface of the sphere, so we need only add together all the contributions ∆S, then multiply the result by this constant. All the elements of area ∆S simply add up to give the surface area of a sphere of radius a; in other words, 4πa2. It follows that
$\int_S {\boldsymbol E}\,{\boldsymbol \cdot}\,d{\boldsymbol S} =(4\pi a^2)\times\dfrac{q}{4\pi\epsilon_0 a^2} = \dfrac{q}{\epsilon_0}$(26)
Equation 26 is a particular instance of a much more general result known as Gauss’ law, and which is of fundamental importance in the theory of electrostatics,
$\displaystyle \left\{\text{the flux of }{\boldsymbol E}\text{ out of} \atop \text{a closed surface }S\right\} = \int_S {\boldsymbol E}\,{\boldsymbol \cdot}\,d{\boldsymbol S} = \dfrac{1}{\epsilon_0} \left\{\text{total charge} \atop \text{within surface }S\right\}$(27)
4 Closing items
4.1 Module summary
- 1
-
The Section 2scalar product of vectors a and b is defined as:
a ⋅ b = | a | | b | cos θ(Eqn 8)
where θ is the angle between the positive directions of a and b.
- 2
-
The Section 2scalar product is commutative. That is:
a ⋅ b = b ⋅ a(Eqn 9)
- 3
-
The Equation 10scalar product of a vector with itself gives the square of the Equation 11magnitude of the vector, i.e. a ⋅ a = | a |2.
The magnitude of the vector a is given by
| a | = (a ⋅ a)1/2 = a(Eqn 11)
- 4
-
The scalar product of two orthogonal vectors is zero i.e. a ⋅ b = 0 when θ = 90°.
- 5
-
For values of θ in the range 0 ≤ θ < 90° the scalar product is positive, while for 90° < θ ≤ 180° the scalar
product is negative.
- 6
-
The Subsection 2.2scalar product in Cartesian scalar component notation is given by:
a ⋅ b = axbx + ayby + azbz(Eqn 15)
- 7
-
The Equation 6magnitude of a vector a is given in scalar component notation by:
| a | = (ax2 + ay2 + az2)1/2(Eqn 6)
- 8
-
The Subsection 2.5projection of a vector b on to a vector a is the scalar quantity
$\dfrac{{\boldsymbol a\,{\boldsymbol \cdot}\,}{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\rvert}$(Eqn 18)
- 9
-
The angle θ between two vectors a and b is:
$\theta = \arccos\,\left(\dfrac{{\boldsymbol a}\,{\boldsymbol \cdot}\,{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\rvert}\right)$
i.e.$\theta = \arccos\,\left[\dfrac{a_xb_x+a_yb_y+a_zb_z}{\sqrt{\left(a_x^2+a_y^2+a_z^2\right)}\sqrt{\left(b_x^2+b_y^2+b_z^2\right)}}\right]$(Eqn 17)
- 10
-
The Subsection 3.1work done by a constant force F acting on a body which undergoes a linear displacement s is F ⋅ s. In the general case where F is variable and the path is non-linear, then the work done by F as the body goes from A to B is given by the line integral
$\displaystyle \int_{\rm A}^{\rm B} {\boldsymbol F}\,{\boldsymbol \cdot}\,d{\boldsymbol S}$
- 11
-
If a body of weight W moves under gravity so that its vertical height above a given level changes from h1 to h2, then the work done by W is | W | (h1 − h2 ).
- 12
-
In a uniform electric field E, the work done by the electric force on a charge q which undergoes a linear displacement s is
F ⋅ s = qE ⋅ s(Eqn 22)
In the general case, where E is non–uniform and the path is non-linear, the work done by the electric force as the charge moves from A to B is given by the line integral
work done = $\displaystyle q\int_{\rm A}^{\rm B} {\boldsymbol E}\,{\boldsymbol \cdot}\,d{\boldsymbol S}$
- 13
-
The electrical potential difference between points A and B in an electric field E is given by
VB − VA = $-\displaystyle \int_{\rm A}^{\rm B} {\boldsymbol E}\,{\boldsymbol \cdot}\,d{\boldsymbol S}$
- 14
-
The surface integral $\int_S {\boldsymbol E}\,{\boldsymbol \cdot}\,d{\boldsymbol S}$ is known as the Subsection 3.5flux of the vector field E across the surface S.
- 15
-
line integralLine integrals and surface integralsurface integrals are merely limits of sums.
4.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of this module.
- A2
-
Define the scalar product of two vectors.
- A3
-
List and explain the properties of the scalar product.
- A4
-
Evaluate the scalar product in terms of the Cartesian scalar components of the vectors.
- A5
-
Express the magnitude of a vector in terms of the Cartesian scalar components of the vector.
- A6
-
Find the projection of one vector on to another.
- A7
-
Use the scalar product to find the angle between two vectors.
- A8
-
Find the work done by a constant force which acts on a body undergoing a linear displacement.
- A9
-
Give a general expression for the work done by a variable force acting on a body which moves along a non–linear path. (You are not expected to be able to calculate line integrals.)
- A10
-
Evaluate the work done by the weight of a body when it moves under gravity from one vertical level to another.
- A11
-
Find the work done by the electric force on a charge which undergoes a linear displacement in a uniform electric field.
- A12
-
Give a general expression for the work done by an electric force acting on a charge which moves in an electric field, and explain how the electric potential difference is related to this expression.
- A13
-
Use the scalar product of force and velocity to find the power associated with a force which acts on a moving body.
- A14
-
Appreciate that the flux of a vector field through a surface is the limit of a sum which is usually written in the form of a surface integral. (You are not expected to be able to calculate surface integrals.)
Study comment You may now wish to take the Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A1, A2 and A3)
Define the scalar product of two vectors and from the definition show that the scalar product is commutative. Explain the condition required for the scalar product of two non–zero vectors to be zero.
Answer E1
The scalar product of vectors a and b is defined in Equation 8,
a ⋅ b = | a | | b | cos θ(Eqn 8)
where θ is the angle between a and b. From this definition a ⋅ b = | a | | b | cos θ = | b | | a | cos θ = b ⋅ a. Therefore the scalar product is commutative. For the scalar product to be zero if a and b are both non-zero, cos θ must be zero. This means that θ = arccos(0) = 90°, 270°, etc. We select θ = 90° as relevant to the context of our vectors. Therefore, the scalar product is zero if the vectors are orthogonal.
(Reread Subsection 2.2 if you had difficulty with this question.)
Question E2 (A4, A5 and A7)
Find the angle between the vectors a = (i + 2 j + 3 k) and b = (3 i + 2 j + k).
Answer E2
From Equations 16 and 17
$\theta = \arccos\,\left(\dfrac{{\boldsymbol a}\,{\boldsymbol \cdot}\,{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\rvert}\right)$(Eqn 16)
$\theta = \arccos\,\left[\dfrac{a_xb_x+a_yb_y+a_zb_z}{\sqrt{\left(a_x^2+a_y^2+a_z^2\right)}\sqrt{\left(b_x^2+b_y^2+b_z^2\right)}}\right]$(Eqn 17)
$\theta = \arccos\,\left(\dfrac{{\boldsymbol a}\,{\boldsymbol \cdot}\,{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\rvert}\right) = \arccos\,\left(\dfrac{(3+4+3)}{\sqrt{1+4+9\os}\sqrt{9+4+1\os}}\right)$
$\phantom{\theta }= \arccos \dfrac{10}{14} = \arccos \dfrac57 = 44.4°$
(Reread Subsection 2.3Subsections 2.3 and Subsection 2.42.4 if you had difficulty with this question.)
Question E3 (A6)
Determine the projection of vector b = (2, −3, −2) on to vector a = (1, 2, −4).
Answer E3
From Equation 18,
$\dfrac{{\boldsymbol a\,{\boldsymbol \cdot}\,}{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\rvert} = \dfrac{a_xb_x + a_yb_y + a_zb_z}{\sqrt{a_x^2+a_y^2+a_z^2}}$(Eqn 18)
the projection of b on to a is
$\dfrac{{\boldsymbol a\,{\boldsymbol \cdot}\,}{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\rvert} = \dfrac{2-6+8}{\sqrt{1+4+16\os}} = \dfrac{4}{\sqrt{21\os}} = 0.873$
(Reread Subsection 2.3Subsections 2.3 and Subsection 2.52.5 if you had difficulty with this question.)
Question E4 (A4, A5, A7 and A8)
Find the work done by a force F = (5 i − j + 2 k) N which acts on a body that undergoes a displacement s = (i + 2 j + 2 k) m, and determine the angle between F and s.
Answer E4
From Equation 20, the work done by a constant force F = (5 i − j + 2 k) N is given by
W = F ⋅ s(Eqn 20)
where the displacement s = (i + 2 j + 2 k) m.
So work done = F ⋅ s = (5 − 2 + 4) J = 7 J.
The angle between F and s can be obtained from Equation 16:
$\theta = \arccos\,\left(\dfrac{{\boldsymbol a}\,{\boldsymbol \cdot}\,{\boldsymbol b}}{\lvert\,{\boldsymbol a}\,\lvert\,\lvert\,{\boldsymbol b}\,\rvert}\right)$(Eqn 16)
$\theta = \arccos\,\left(\dfrac{{\boldsymbol F}\,{\boldsymbol \cdot}\,{\boldsymbol s}}{\lvert\,{\boldsymbol F}\,\lvert\,\lvert\,{\boldsymbol S}\,\rvert}\right) = \arccos \dfrac{7}{\sqrt{25+1+4\os}\sqrt{1+4+4\os}}$
$\phantom{\theta }= \arccos \dfrac{7}{3\sqrt{30\os}} = 64.8°$
(Reread Subsection 2.3Subsections 2.3, Subsection 2.42.4 and Subsection 3.13.1 if you had difficulty with this question.)
Question E5 (A10 and A11)
Find the distance a body must fall vertically in order that its weight of magnitude 1.0 N does the same work as the electric force acting on a charge of 1.0 × 10−6 C which undergoes a displacement s = (4, 1, 5) m in an electric field E = 103(2, −3, 1) N C−1.
Answer E5
From Equation 22, the work done by the electric force exerted on a charge q = 1 × 10−6 C which undergoes a displacement s = (4, 1, 5) m in an electric field E = 103 (2, −3, 1) N C−1 is given by
q E ⋅ s = 10−6 × 103 (8 − 3 + 5) J = 10−2 J
From Subsection 3.2, the work done by the weight W of a body falling a distance d is given by
work done = | W | d
It follows that 10−2 J = (1 N × d) and therefore d = 10−2 m.
(Reread Subsection 2.3Subsections 2.3, Subsection 3.13.1, Subsection 3.23.2 and Subsection 3.33.3 if you had difficulty with this question.)
Question E6 (A12)
If A and B are the initial and end points of the displacement s in Question E5, find the electric potential difference VB − VA.
Answer E6
Using the method of Example 2,
VB − VA = − E ⋅ s = −104 J C−1 or −104 V.
(Reread Subsection 3.3 if you had difficulty with this question.)
Question E7 (A13)
A force F = (2, −3, 4) N acts on a body which undergoes a displacement s1 = (5, −2, −1) m in 4 seconds, followed by a displacement s2 = (4, −4, −5) m in 5 seconds. Determine the average power for each of the separate displacements.
Answer E7
In Subsection 3.4, the average power is defined as the average rate of work done. Therefore, average power is the work done divided by the time taken. For the displacement s1, the average power is given by:
$\dfrac{{\boldsymbol F}\,{\boldsymbol \cdot}\,{\boldsymbol s}_1}{{\rm time}_1} = \dfrac{10+6-4}{4}\,{\rm W} = 3\,{\rm W}$
Similarly, for the displacement s2, the average power is given by:
$\dfrac{{\boldsymbol F}\,{\boldsymbol \cdot}\,{\boldsymbol s}_2}{{\rm time}_2} = \dfrac{8+12-20}{5}\,{\rm W} = 0\,{\rm W}$
The fact that the work done by F is zero over the second displacement implies that F and s2are orthogonal.
(Reread Subsection 2.3Subsections 2.3 and Subsection 3.43.4 if you had difficulty with this question.)
Question E8 (A13 and A14)
In Example 3 we found the flux of the electric field E due to a point charge q placed at the centre of a sphere of radius a. What happens to this flux if (a) we double the charge, and (b) we double the radius of the sphere?
Answer E8
From Equation 26:
$\int_S {\boldsymbol E}\,{\boldsymbol \cdot}\,d{\boldsymbol S} =(4\pi a^2)\times\dfrac{q}{4\pi\epsilon_0 a^2} = \dfrac{q}{\epsilon_0}$(Eqn 26)
(a) if we double the charge then the flux doubles, but (b) the flux is independent of the radius of the sphere and
so if we double the radius the flux remains unchanged.
(Reread Subsection 3.5 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment It is assumed that you already have some basic knowledge of the concepts of scalars and vectors, and of vector algebra.
You should be familiar with the Cartesian unit vectorsCartesian (unit vector) form of a vector and the ordered triple representation of a vector i (although we will review them briefly for you here), and you should be able to apply both forms of a vector to scaling_of_a_vectorscaling, vector addition and vector_differencevector subtraction. You should be familiar with terms such as unit vector, magnitude of a vectormagnitude of a vector, component vectors, resolution_of_a_vectorresolving a vector into component vectors, scalar_components_of_a_vectorscalar components of a vector, force, weight, displacement, velocity, and electric charge; also Pythagoras’ theorem and trigonometric identities.
If you are uncertain about any of these terms then you can review them by reference to the Glossary which will indicate where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.