MATH 2.4: Introducing scalars and vectors |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
Many of the quantities that physicists use are easy to specify; measurements of mass, length, time, area, volume and temperature can all be expressed as simple numbers together with appropriate units of measurement. Such quantities are known as scalar quantities or scalars. However, some quantities are more tricky to deal with. For instance, if you want to travel from one place to another you will not only want to know how far apart the two places are, you will also need to know the direction that leads from one to the other. The physical quantity that combines distance and direction is called displacement and is clearly more complicated than distance alone. Displacement is a simple example of a large class of physical quantities known collectively as vector quantities or vectors. A detailed understanding of vectors and how to use them is crucial to many parts of physics, particularly mechanics and electromagnetism.
This module provides an introduction to the mathematical treatment of vectors. Section 2 gives a definition of vector quantities that separates them from simpler scalar quantities – such as mass and distance – that are also defined. This section also describes the graphical representation of vectors and the notation used to distinguish vectors from scalars, both in print and in handwritten work. Section 3 introduces some of the basic operations of vector algebra such as scaling (multiplication by a scalar), vector addition and vector subtraction. It aims to make clear the meaning of vector equations such as 3 a − 2 b = 0. The section ends with a discussion of the way in which a given vector may be split–up (resolved) into component vectors – a process that is of importance in many practical problems.
Throughout the module the emphasis is on basic ideas and geometric (graphical) methods. The algebraic methods that are more frequently used by those already familiar with vectors are mentioned briefly in a short conclusion (Section 4) but their full development is left to other modules. Since it is those methods that are best suited to tackling three–dimensional problems, most of the questions in this module are restricted to two–dimensional situations on idealized planes or flat surfaces. However, even though the discussion is mainly restricted to two dimensions, the significance of vectors is amply demonstrated as is the importance of always using vector notation clearly and correctly.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
In terms of a strict interpretation of vector and scalar quantities, what is wrong with each of the following statements?
(a) The velocity of light travelling through a vacuum (usually denoted by c) is approximately 3 × 108 m s−1.
(b) The acceleration due to gravity (usually denoted by g) near the surface of the Earth is approximately
10 m s−2.
(c) The mass of your head pushes down on your neck.
Answer F1
(a) The velocity of light is a vector quantity so its complete specification requires a magnitude and a direction. No direction is given in the statement, only the speed of light has been specified.
(b) Similarly, acceleration is a vector quantity so its complete specification requires a magnitude and a direction. It is conventional to refer to g as the ‘acceleration due to gravity’ but in strict vector terms it should be called the magnitude of the acceleration due to gravity.
(c) Mass is a scalar quantity, so it has no associated direction and cannot push down on anything. Forces exerted by your head (by virtue of gravity acting on its mass) do have direction and can ‘push down’ on your neck.
Question F2
a is a displacement of 4.32 km due north, and b is a displacement of 2.40 km due east.
(a) What is the magnitude and the direction of the displacement 3 a − 5 b?
(b) Given a specified line, any vector may be expressed as the sum of two (orthogonal) component vectors, one parallel to the given line and the other at right angles to that line. What is the magnitude of the (orthogonal) component vector of 3 a − 5 b that points in the direction 20° west of north?
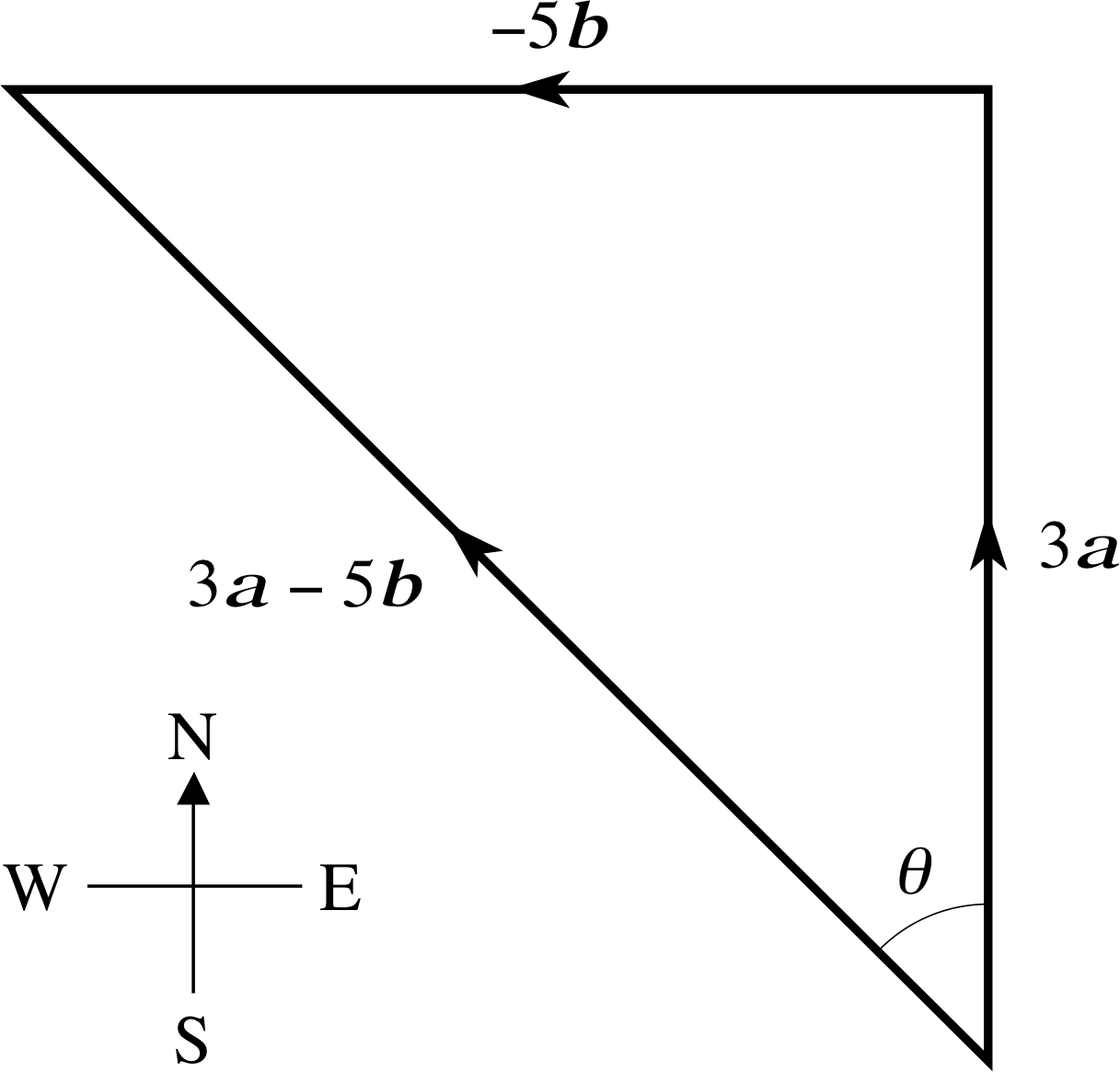
Figure 14 See Question F2.
Answer F2
(a) The displacement 3 a − 5 b is shown in Figure 14. Its magnitude can be determined graphically or algebraically by means of Pythagoras’s theorem. Using this latter technique:
| 3 a − 5 b |2 = 9 | a |2 + 25 | b |2
i.e. | 3 a − 5 b |2 = [9 (4.32)2 + 25 (2.40)2] km2
Thus,| 3 a − 5 b | = 17.7 km
The displacement is at an angle θ west of north, where
$\theta = \arctan\left(\dfrac{\lvert\,5\,{\boldsymbol b}\,\rvert}{\lvert\,3\,{\boldsymbol a}\,\rvert}\right) = \arctan\left(\dfrac{12.00}{12.96}\right) = 42.80°$
(b) The orthogonal component vector in the given direction will be inclined at 22.80° (= 42.80° − 20°) to 3 a − 5 b so its magnitude will be
| 3 a − 5 b | cos 22.80° = (17.7) 0.922 km = 16.3 km
1.3 Ready to study?
Study comment Relatively little background knowledge is required to study this module. Terms such as mass, electric charge and temperature are used and it is assumed that you know something about measuring such quantities using SI units, but you do not need to know precise definitions or exact meanings. It is also assumed that you have met Newton’s laws of motion before, but again you do not need to know those laws in detail in order to study the module. (Indeed, this module would be good preparation for a thorough study of Newton’s laws.) There are some mathematical topics, however, with which you will need to be familiar before starting to study; they are the subject of the following questions. Consult the Glossary for references to any terms that are unfamiliar.
| point | x–coordinate | y–coordinate |
|---|---|---|
| A | 1 | 1 |
| B | −3 | 1 |
| C | −3 | 4 |
Question R1
Draw a set of two–dimensional Cartesian axes. Label the horizontal axis x and the vertical axis y. Using the axes you have drawn, plot the three points A, B and C the coordinates of which are given in Table 1. Draw the right–angled triangle that has the points A, B and C at its corners. Write down the lengths of sides AB and BC of that triangle, and use Pythagoras’s theorem to work out the length of the side CA.
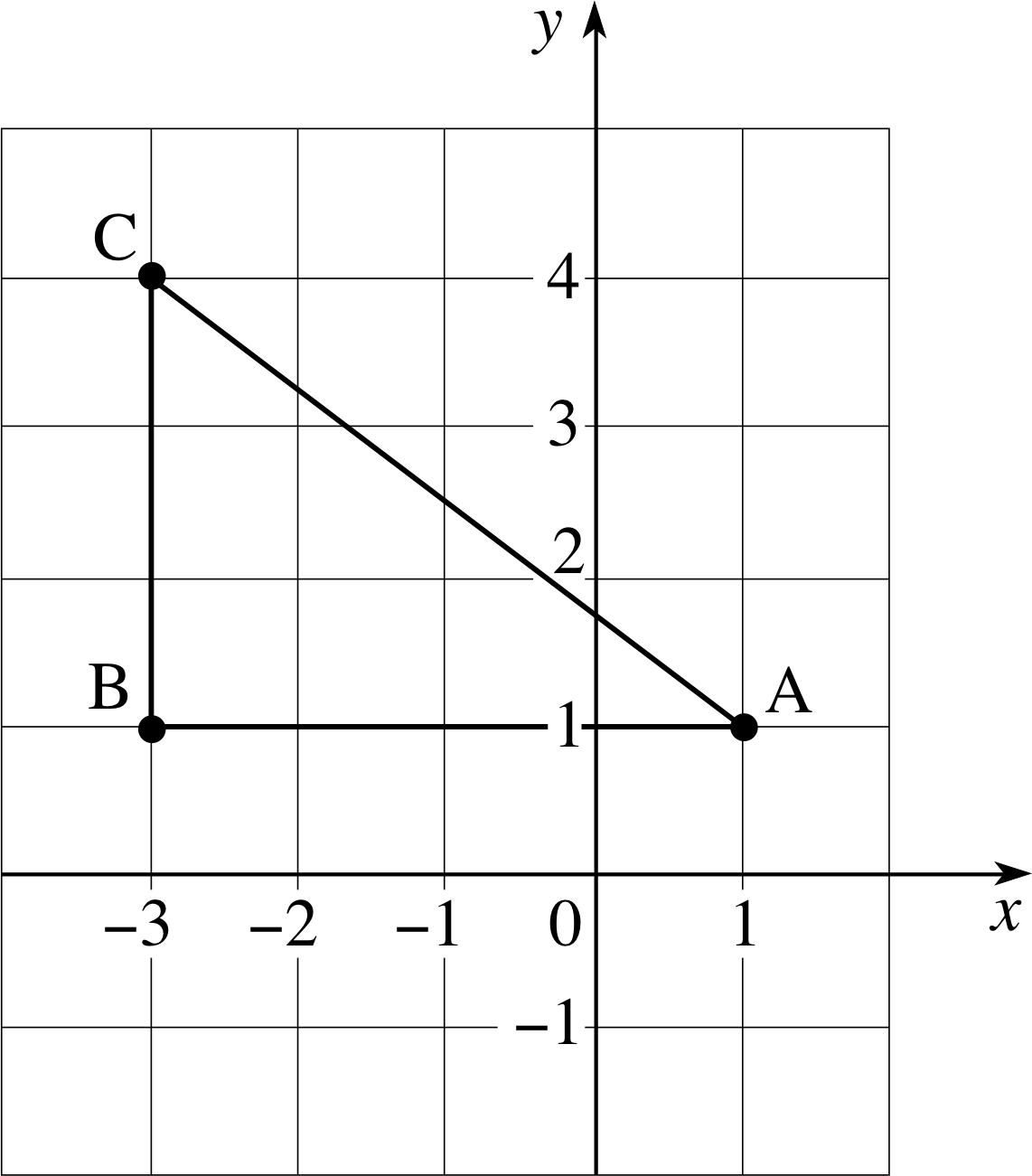
Figure 15 See Question R1.
Answer R1
See Figure 15. (You are not expected to draw the complete grid.)
Length of side AB = 1 − (−3) = 4
Length of side BC = 4 − 1 = 3
Length of side CA = $\sqrt{(4)^2 + (3)^2} = \sqrt{25\os} = 5$
This side is called the hypotenuse.
(For details about Cartesian coordinates and their use in the evaluation of lengths see under coordinatescoordinate geometry in the Glossary.)
Question R2
Using the triangle given in the answer to Question R1 (Figure 15), and indicating the length of side CA by c and the angle $C\hat AB$ by θ, write down expressions for the lengths of sides AB and BC in terms of the length c, the angle θ, and the basic trigonometric ratios. What is the value (in degrees) of the angle θ?
Answer R2
It follows from the definitions of the trigonometric ratios that:
Length of side AB = c cos θ
Length of side BC = c sin θ
Thus, $\dfrac{\sin\theta}{\cos\theta} = \tan\theta = \dfrac{\text{length of side BC}}{\text{length of side AB}} = \dfrac{3}{4} $
It follows that θ = arctan(0.75) = 36.9°.
(The inverse trigonometric function arctan θ is discussed in the Glossary; some authors prefer to call it tan−1 θ.)
Question R3
The modulus of a quantity x is written | x | and represents the absolute value of x. Evaluate the following expressions and complete the equations.
(a) | 3 | = (b) | −13 | = (c) | (−12)(3.1) | = (d) | (−12.4) / (2) | =
Answer R3
According to the Glossary, the modulus | x | is defined by the requirement
if x ≥ 0 | x | = x and | −x | = x
Thus, | x | is always a non–negative quantity, irrespective of the sign of x itself.
(a) | 3 | = 3
(b) | −3 | = 3
(c) | (−2)(3.1) | = | −6.2 | = 6.2
(d) | (−2.4)/2 | = | −1.2 | = 1.2
2 Scalars and vectors
2.1 Scalars and scalar quantities
Many important physical quantities, such as length, mass and temperature, can be completely specified by a single number together with an appropriate unit of measurement. For instance, it makes perfectly good sense to say that the length of an object is 1.42 m or that the mass of an object is 12.2 kg. Quantities that can be specified in this simple and straightforward way are called scalar quantities. Thus:
Scalar quantities are physical quantities that can be completely specified by a single number together with an appropriate unit of measurement.
Different values of a given scalar quantity may be easily added, subtracted, multiplied or divided. In fact, all the elementary operations of arithmetic apply to values of a scalar quantity just as they do to ordinary numbers. So, if a, b and c are three values of a given scalar quantity (three masses, say) then we know that:
a + b = b + a(1)
ab = ba(2)
a + 0 = a(3)
a × 1 = a(4)
(a + b) + c = a + (b + c)(5) i
a (bc) = (ab)c(6)
a (b + c) = ab + ac(7)
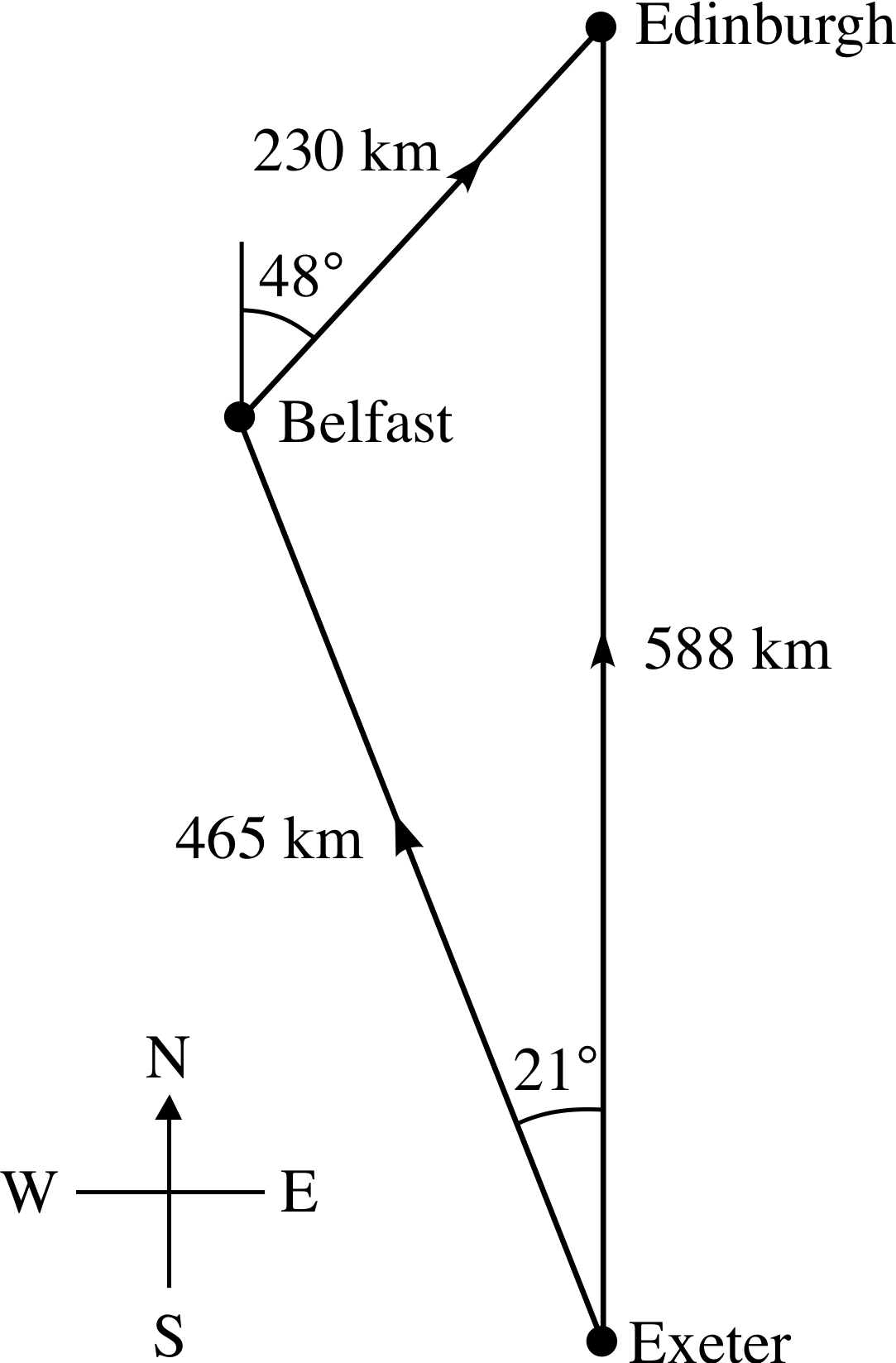
Figure 1 An idealized map showing the relative locations of Belfast, Edinburgh and Exeter.
Scalar quantities are often referred to simply as scalars. There is nothing very surprising about the behaviour of scalars; their properties seem obvious and, indeed, they are obvious. What is much more interesting is that there are many physical quantities that are not scalars.
2.2 Vectors and vector quantities
Figure 1 shows the relative locations of Belfast, Edinburgh and Exeter, three of the major cities in the UK. If you were asked to describe the location of Edinburgh relative to Exeter what would you say? You might start by stating that Edinburgh is 588 km from Exeter, but that would not answer the question. Although you would have defined the distance from Exeter to Edinburgh you would still not have fully defined the relative position. To provide a full description of the location you have to give the distance and the direction.
The physical quantity that describes the location of one point (Edinburgh, say) with respect to another point (Exeter, say) is called displacement. The displacement from Exeter to Edinburgh is 588 km in the direction due north.
✦ What is the displacement from Edinburgh to Exeter?
✧ 588 km, due south.
Displacement, unlike distance, cannot be specified by a number together with an appropriate unit of measurement; an additional ingredient is required – a direction. Of course, the direction can be specified in a number of different ways, but its presence is unavoidable.
Question T1
What is the displacement: (a) from Exeter to Belfast? (b) from Belfast to Edinburgh?
Answer T1
(a) The displacement from Exeter to Belfast is 465 km, at 21° west of north.
(b) The displacement from Belfast to Edinburgh is 230 km, at 48° east of north.
(You may have specified the directions differently, but your specifications should be equivalent to those given in the answer.)
It is important to note that displacements are entirely specified by two items of information:
- A distance (this is called the magnitude_of_a_vector_or_vector_quantitymagnitude of the displacement and must be a non–negative scalar quantity). i
- A direction (in a two–dimensional plane this is often specified in terms of compass bearings, but other methods can be used; in three dimensions other methods must be used).
The two end–points of the displacement do not enter into this specification and are immaterial to the displacement itself. Thus, a displacement of 588 km due north starting from Exeter is the same displacement as one of 588 km due north from Belfast, even though one ends in Edinburgh and the other in the sea. In fact, any two displacements are equal if they have the same magnitude and the same direction.

Figure 1 An idealized map showing the relative locations of Belfast, Edinburgh and Exeter.
Question T2
Which of the following displacements are equal to the displacement from Edinburgh to Belfast?
(a) A displacement of magnitude −230 km, 48° west of south.
(b) A displacement of magnitude 230 km, 48° east of north.
(c) A displacement of magnitude 230 km, 42° south of west.
Answer T2
Only displacement (c) is equal to the displacement from Edinburgh to Belfast. Displacement (a) is in the exactly opposite direction and displacement (b) has a negative magnitude – which is meaningless.
(Note: Magnitudes can never be negative. Negative magnitudes do not indicate a reversal of direction – they are simply meaningless.)
Displacements are just one example of a large class of physical quantities known as vector quantities i The common characteristics of all vector quantities can be summarized as follows:
Vector quantities are physical quantities that can be completely specified by a magnitude and a direction.
Note that the general ‘magnitude’ referred to here is always a non–negative scalar quantity, just as distance (the magnitude of a displacement) must always be a non–negative scalar quantity. The magnitude of any vector quantity can be thought of as the ‘size’ or ‘length’ of that vector.
Apart from displacement, other important vector quantities include velocity, acceleration, and force. You may not be familiar with all of these quantities, so a few words about each should help to define it and to underline its vector nature.
The velocity of an object is a vector quantity that describes how fast the object is moving and the direction in which it is travelling. The magnitude of the velocity is called the speed and is a non–negative scalar quantity. The direction of the velocity is the direction of motion.
The acceleration of an object is a vector quantity that describes the rate of change of the object’s velocity. Acceleration is a vector quantity because it involves a change in a vector quantity, velocity, and such a change requires both a magnitude and a direction for its complete specification. For example, a car travelling in a fixed direction at ever increasing speed is accelerating because the magnitude of its velocity is changing, whereas a car travelling in a circle at a fixed speed is accelerating because the direction of its velocity is changing. Any change in the magnitude or the direction of the velocity, or any combination of the two, constitutes an acceleration. Similarly, the rate of change of any other vector quantity must be a vector quantity.
According to Newton’s laws of motion, when an object accelerates it does so because an unbalanced (i) force acts upon it. Roughly speaking, force is the ‘push’ or ‘pull’ that causes (or tends to cause) acceleration. Newton’s second law asserts that the acceleration of a body of fixed mass is proportional to the force that acts upon it. We know that the ‘effect’ of a force depends on its direction as well as its strength, so force is a vector. The ‘effect’ of a force, according to Newton, is an acceleration, which is also a vector. More specifically, the magnitude of the acceleration is proportional to the magnitude of the force and the direction of the acceleration is the same as the direction of the force.
Question T3
Which of the following are vector quantities; energy, distance, time, electric charge, rate of change of acceleration, altitude above sea level?
Answer T3
Only rate of change of acceleration is a vector, since it alone requires a direction as part of its complete specification. Energy, distance and time can all be expressed as single numbers together with appropriate units, so they are all scalars. Electric charge is also a scalar, for the same reason, even though it may be positive or negative. Similarly, altitude above sea level is a scalar since there is no need to include any directional information (such as ‘upwards’) when specifying values of the altitude – it is enough to say 10 m, for example.
Just as scalar quantities are often referred to as scalars, so vector quantities are often called vectors. It is possible to draw a distinction between vectors and vector quantities on the one hand and scalars and scalar quantities on the other. Vector and scalar quantities are physical quantities while vectors and scalars are the mathematical entities that are used to represent those physical quantities. Although it is important to distinguish between real things and their mathematical representations we shall not pursue that distinction here. In what follows the terms vector and vector quantity will be used interchangeably, as will scalar and scalar quantity.
Question T4
How would you counter the following assertions (both of which are wrong)?
(a) The velocity of a particular object (such as my car) cannot be a vector since it is not completely specified by a magnitude and a direction – its complete specification also requires the identification of the moving object (my car).
(b) Displacement cannot be a vector since its complete specification requires the definition of the various compass bearings (or something similar) and not merely the statement of a magnitude and a direction.
Answer T4
(a) It is the velocity of the car which is to be specified, not the car itself. Whereas the specification of the car includes information on its ownership, the velocity itself does not. The velocity so defined is completely specified by a magnitude and a direction.
(b) This claim is reasonable but misguided. It is indeed necessary to know about compass bearings (or something equivalent) but this is part of the specification of direction and not something separate. So, the statement that a displacement is defined by a magnitude and a direction is still true.
2.3 Representing scalars and vectors
Everybody knows how to represent a scalar quantity such as mass or length when writing equations or drawing diagrams; just choose an appropriate letter or symbol to represent the quantity concerned (m or l say) and write it down wherever the scalar quantity is to be represented. It is taken for granted that the chosen symbol indicates the appropriate units of measurement as well as the number of those units, so it makes good sense to write statements such as:
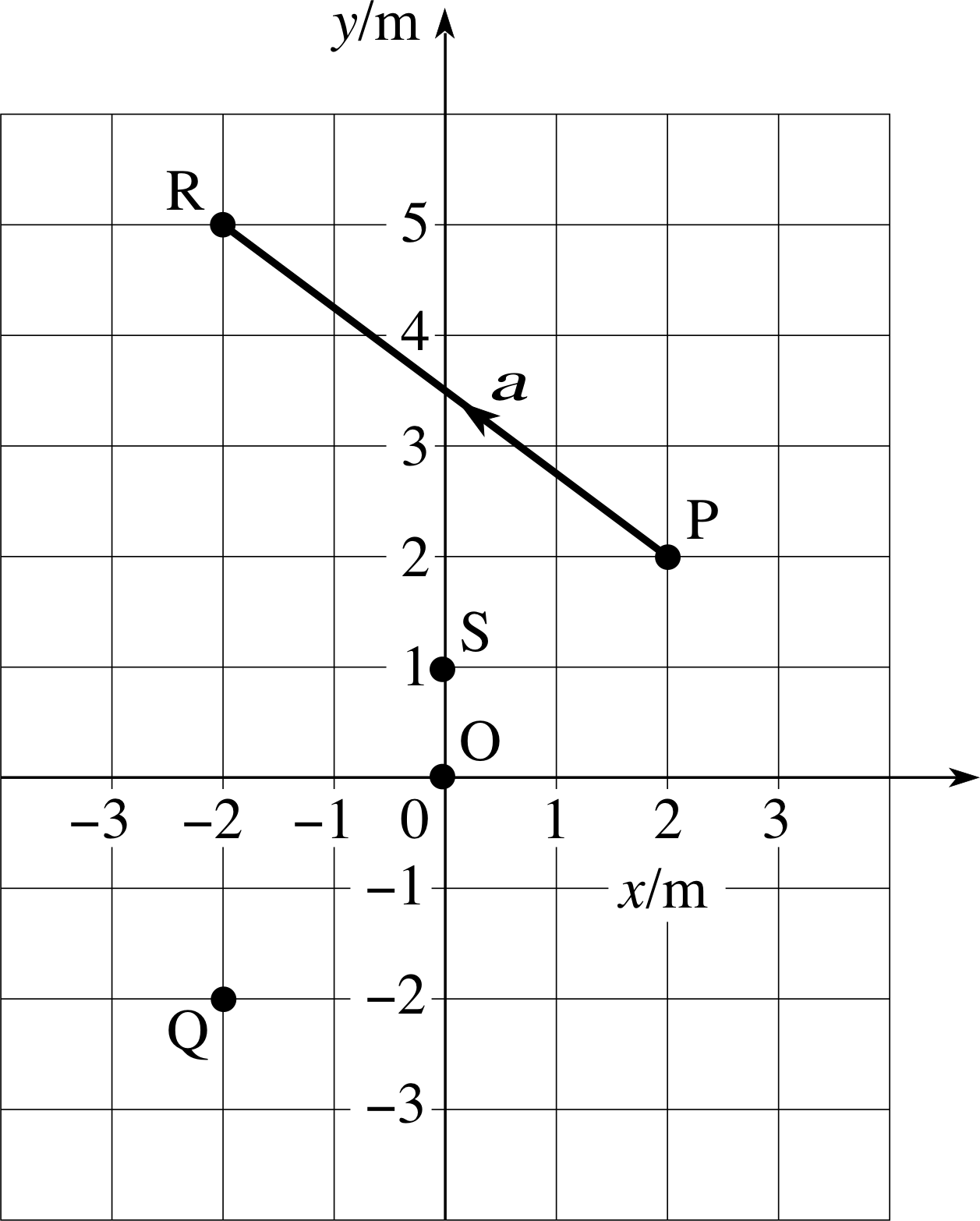
Figure 2 A representation of the locations of the five points O, P, Q, R and S in a two–dimensional plane.
If length l = 6 m, then l2 = 36 m2
Unfortunately, dealing with vectors is a good deal more difficult since directions are involved as well as magnitudes. When drawing diagrams the problem is not too bad since, as in Figure 1, a vector can be represented by a line labelled with the appropriate magnitude and pointed in the appropriate direction. The direction of the line is usually indicated by an arrowhead at the end of the line or by a pointer somewhere along the line. For this reason, such lines are usually referred to as arrows or directed line segments.
Figure 2 shows five points O, P, Q, R and S, located in a two–dimensional plane. The positions of the five points can be specified by their Cartesian coordinates (x, y) with respect to the axes x and y shown in the figure. (Note that all measurements are expressed in metres.) Also included in the figure is a directed line segment from P to R. This represents the displacement from P to R.
One obvious way of representing the displacement from P to R symbolically is to write it as $\overrightarrow{\rm PR}$. This is a clear if somewhat cumbersome notation that may easily be applied to other displacements.
Question T5
Using Figure 2: (a) Find the magnitude of $\overrightarrow{\rm PR}$, (b) Describe the direction of $\overrightarrow{\rm PR}$, and (c) Find the magnitude of $\overrightarrow{\rm OQ}$.
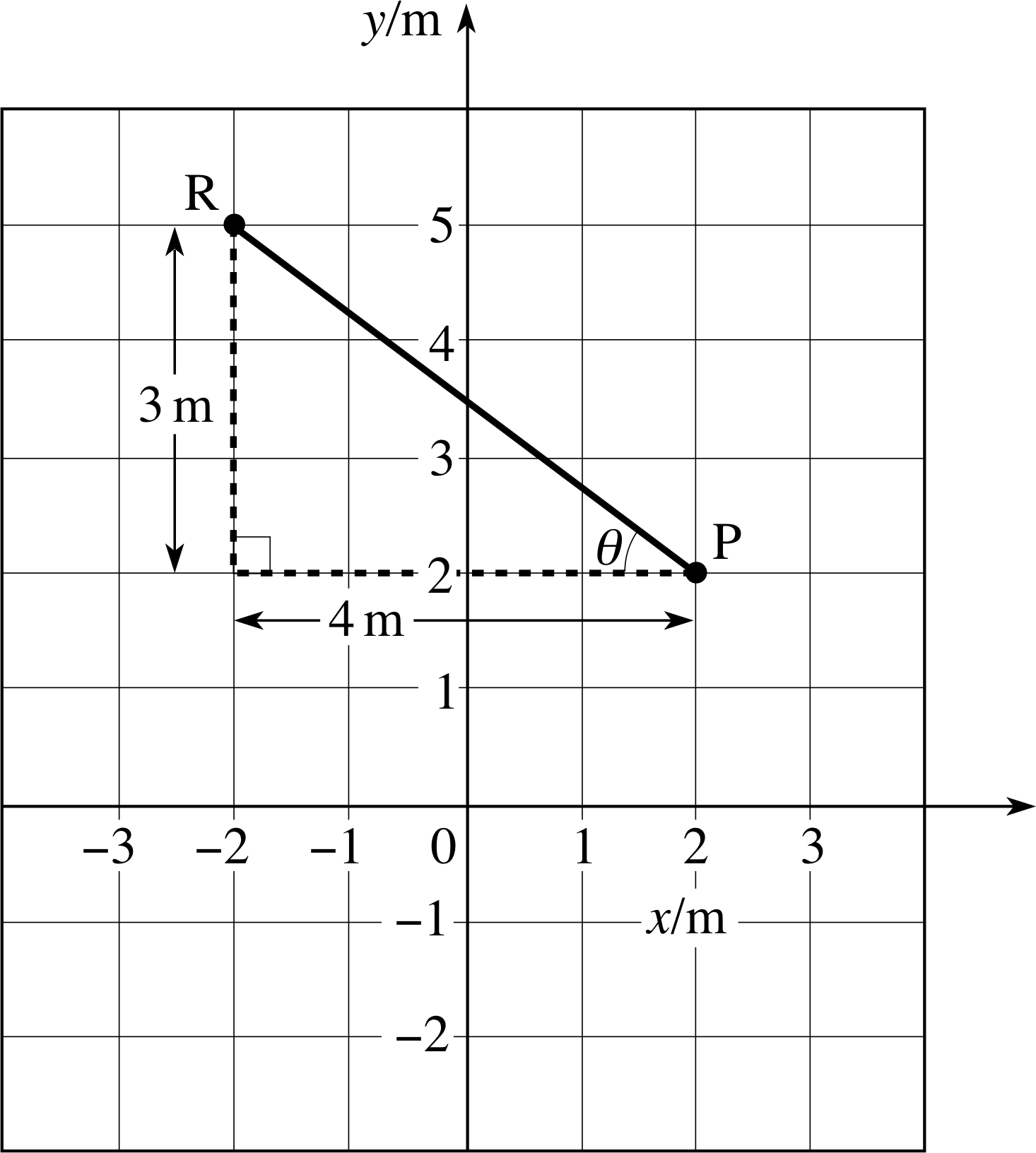
Figure 16 See Question T5.
Answer T5
(a) You can find the magnitude of $\overrightarrow{\rm PR}$ just by measuring its length with a ruler and then interpreting your measurement in terms of the scale indicated on the Cartesian axes. The magnitude of the displacement $\overrightarrow{\rm PR}$ is 5 m.
Alternatively, you may treat the line PR as the hypotenuse of a right–angled triangle, as shown in Figure 16 and use Pythagoras’s theorem to deduce that the magnitude of $\overrightarrow{\rm PR}$ is
$\rm \sqrt{(3\,m)^2+(4\,m)^2}= \sqrt{25\os}\,m = 5\,m$.
(b) $\overrightarrow{\rm PR}$ points in the direction from P to R. The direction may be described by saying that the angle θ in Figure 16 is
arctan(3/4) = arctan 0.75 = 36.9°
(c) Using Pythagoras’s theorem, the magnitude of the displacement $\overrightarrow{\rm OQ}$ is
$\rm \sqrt{(2\,m)^2+(2\,m)^2} = \sqrt{8\os}\,m = 2.83\,m$.
Another way of representing vectors in printed material is to symbolize them by bold–face type, thus the bold a in Figure 2 is yet another way of representing the displacement $\overrightarrow{\rm PR}$. Indeed, it makes sense to write
${\boldsymbol a} = \overrightarrow{\rm PR}$
This new symbol (the bold a) does not have any obvious link with the points P and R, which may be regarded as an advantage or a disadvantage. However, one very definite bonus is that emboldening is applicable to all kinds of vector quantities (velocities, accelerations, forces, etc.) and not just displacements. The bold–typeface convention is the most widely used method of representing vectors and will be used throughout FLAP.
Distinguishing vectors by bold–face type is fine in print, but it presents a problem for those using pens or pencils. How can you show that a is a vector when you write it down? Fortunately there is an easy answer to this problem. When authors are preparing material to be printed they show that an item should be set in bold–face type by putting a wavy underline beneath it. Thus, what is written as $\underset{\boldsymbol{\raise 6pt \sim}}{a}$ will be printed as a. You are encouraged to adopt this convention for distinguishing vectors so that you will never make the mistake of writing down a nonsensical equation such as
$\underset{\boldsymbol{\raise 6pt \sim}}{a} = 5\,{\rm m}$
✦ Why is this equation nonsensical?
✧ $\underset{\boldsymbol{\raise 6pt \sim}}{a}$ is a vector, it has both magnitude and direction. 5 m is simply a scalar, it has no ‘direction’. It makes no sense to equate a quantity that has direction with one that does not.
Question T6
In Figure 2 the vectors b, c, d and e are defined as follows:
b = $\overrightarrow{\rm PS}$, c = $\overrightarrow{\rm OS}$, d = $\overrightarrow{\rm QO}$, e = $\overrightarrow{\rm QR}$
(a) Using a pencil, add directed line segments representing each of these vectors to Figure 2.
(b) Label each of the directed line segments with the appropriate vector symbol.
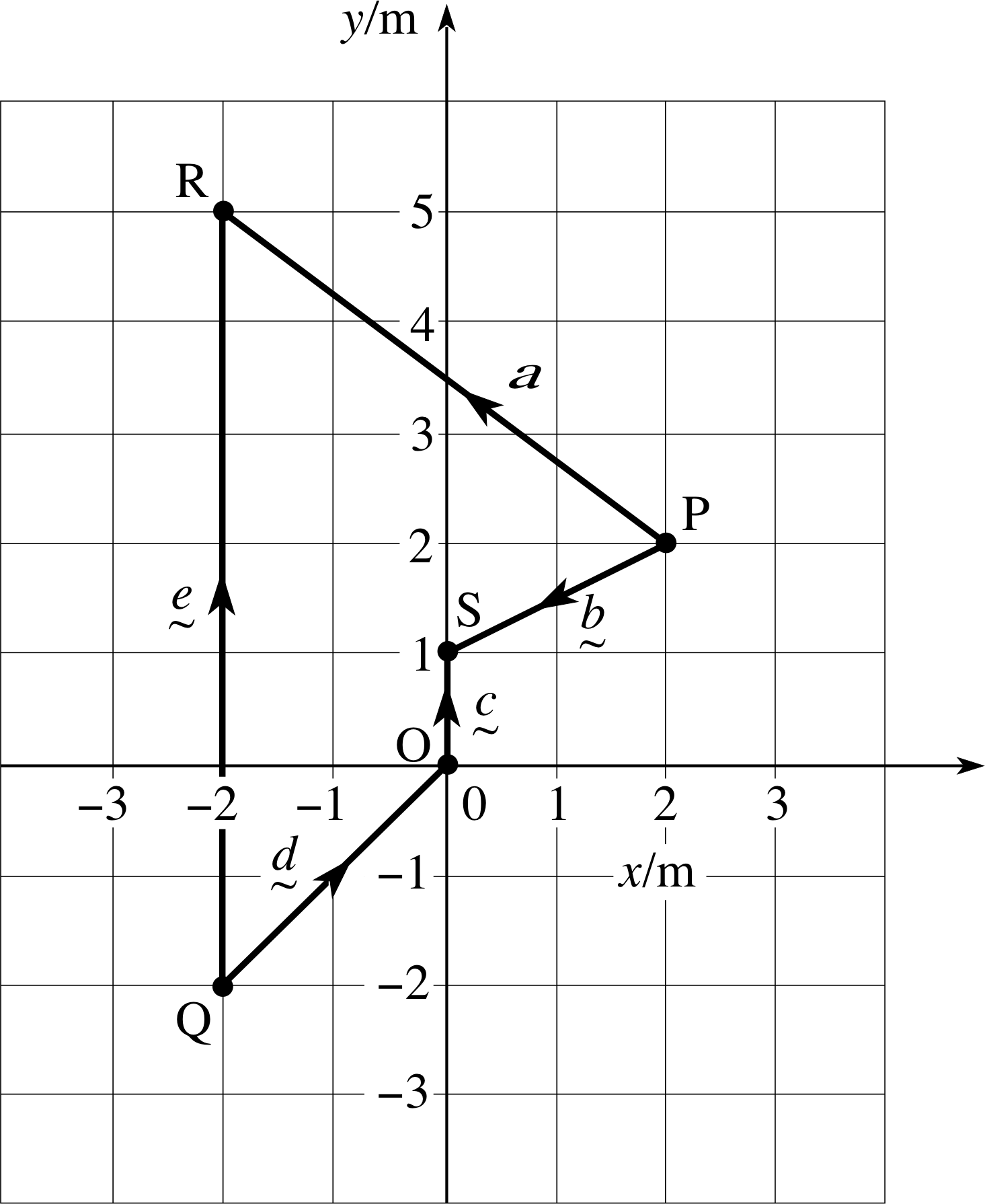
Figure 17 See Question T6.
Answer T6
See Figure 17.
Make sure you have included the wavy underlines beneath the vectors.

Figure 2 A representation of the locations of the five points O, P, Q, R and S in a two–dimensional plane.
Another advantage of the bold–typeface convention for vectors is that it provides a natural way of representing the magnitude of a vector. Given a vector a, its magnitude is conventionally denoted | a |. So, it makes sense to write
| a | = 5 m (In a manuscript: | $\underset{\boldsymbol{\raise 6pt \sim}}{a}$ | = 5 m)
even though it was meaningless to write a = 5 m.
Sometimes, when there is no risk of confusion, the magnitude of a vector is simply represented by the symbol used for the vector itself, but without the emboldening. Thus, you might see
a = | a | = 5 m, or simply a = 5 m
This is obviously much less bother to write, but it is easy to forget that a, being a magnitude, must be non-negative, whereas you are unlikely to forget that something as complicated as | a | cannot be negative.
Question T7
Using your copy of Figure 2 having completed Question T6 and working to three significant figures, evaluate the following quantities:
(a) | $\overrightarrow{\rm RS}$ | (b) | b | and | c | (c) | b | + | c | and | b | | c | (d) | a | + | b | + | c | + | d | + | e | (e) $2\lvert\,{\boldsymbol a}\,\rvert + \dfrac{\lvert\,{\boldsymbol b}\,\lvert\,\lvert\,{\boldsymbol c}\,\rvert}{\lvert\,{\boldsymbol d}\,\rvert}$
Answer T7
(a) Using Pythagoras’s theorem $\lvert\,\overrightarrow{\rm RS}\,\rvert = \rm \sqrt{(2\,m)^2+(4\,m)^2}= \sqrt{20\os}\,m = 4.47\,m$
(b) $\lvert\,{\boldsymbol b}\,\rvert = \rm \sqrt{(2\,m)^2+(1\,m)^2}= \sqrt{5\os}\,m = 2.24\,m$, | c | = 1 m
(c) | b | + | c | = (1 + 2.24) m = 3.24 m, | b | | c | = (2.24 m)(1 m) = 2.24 m2
(d) | a | = 5 m, | b | = 2.24 m, | c | = 1 m, $\lvert\,{\boldsymbol d}\,\rvert = \rm \sqrt{(2\,m)^2+(2\,m)^2} = \sqrt{8\os}\,m = 2.83\,m$, | e | = 7 m
So, | a | + | b | + | c | + | d | + | e | = 18.07 m
(e) $2\lvert\,{\boldsymbol a}\,\rvert + \dfrac{\lvert\,{\boldsymbol b}\,\lvert\,\lvert\,{\boldsymbol c}\,\rvert}{\lvert\,{\boldsymbol d}\,\rvert} = \rm 2(5\,m) + \dfrac{(2.24\,m)(1\,m)}{2.83\,m} = 10\,m + 0.79\,m = 10.79\,m$
Note that the magnitudes of vectors are simply non–negative scalar quantities, so they can be added and subtracted, multiplied and divided just like any other scalar quantities.
The main result of this subsection may be summarized as follows:
By convention, bold–face symbols such as a are used to represent vector quantities. The magnitude of such a vector is represented by | a | and is a non–negative scalar quantity. In diagrams vectors are represented by directed line segments. In handwritten work vectors are distinguished by a wavy underline ($\underset{\boldsymbol{\raise 6pt \sim}}{a}$) and the magnitude of a vector is denoted | $\underset{\boldsymbol{\raise 6pt \sim}}{a}$ |.
3 Introducing vector algebra
Scalar quantities can be added, subtracted, multiplied or divided. So, it is quite possible to form equations and carry out all the normal processes of algebra with scalar quantities. (Finding unknown scalar quantities was probably the first use you ever made of algebra, even if the word ‘scalar’ wasn’t used at the time!) Working with vectors is more difficult because it involves directions as well as magnitudes. Nonetheless, it is possible to make sense of algebraic expressions such as a + b or 3 a − 2 b and to formulate and solve vector equations. This section introduces the basic concepts of vector algebra – a subject that is more fully developed in other modules.
3.1 Scaling vectors
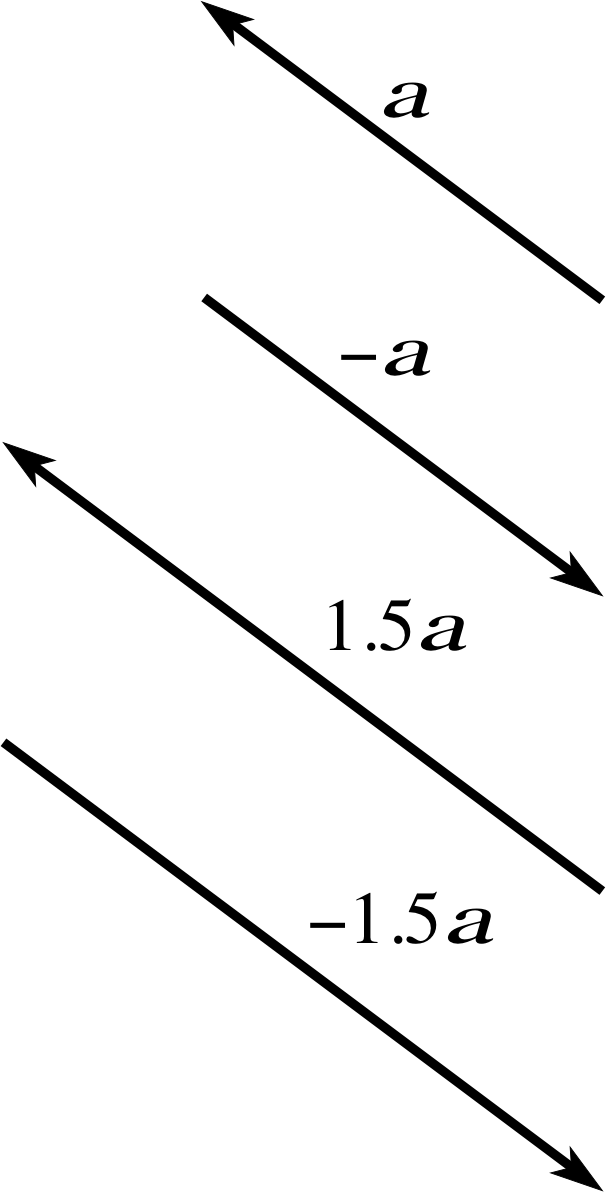
Figure 3 A vector a and three of its scaled counterparts −1 a, 1.5 a and −1.5 a.
The simplest operation of vector algebra is the scaling of a vector, that is the multiplication of a vector by a scalar. For example, if υ is a velocity of 15 m s−1 due north then 2υ is a velocity of 30 m s−1 in the same direction or, to give another example, if a is a displacement of 50 m due east then −3 a is a displacement of 150 m due west. Note that in this last example the inclusion of the minus sign has had the effect of reversing the direction. Some more examples of scaling are shown in Figure 3.
It should be noted that −1 a is usually written −1 a and that 1.5 a could equally well be written (1.5) a or even a (1.5), so the order of the multiplication is unimportant. Nonetheless, it is more conventional to use the form 1.5 a since this is more suggestive of ‘taking 1.5 lots of a’.
In general, if a is a vector and α is a scalar (which may be positive or negative) then α a, the result of scaling_of_a_vectorscaling a by α, is a vector of magnitude | α | | a | that points in the same direction as a if α > 0 and points in the opposite direction to a if α < 0. i
When dealing with vectors, some authors use the term parallel to mean ‘in the same direction’ and the term antiparallel to mean ‘in the opposite direction’. Thus, the vectors a and 1.5 a maybe described as parallel, while a and (−1.5) a are antiparallel. Unfortunately the use of antiparallel, though widespread, is not universal. So, whenever you see the term ‘parallel’ you should take it to mean ‘parallel or antiparallel’ unless the more specialized interpretation is clearly indicated.
Question T8
If a body of mass m = 6 kg has velocity υ of magnitude 5 m s−1 in the direction north-west, what is the magnitude and direction of mv? (In Newtonian mechanics this vector quantity is known as the momentum of the body.)
Answer T8
If m = 6 kg and v = 5 m s−1 north-west, then
mv = 30 kg m s−1 north-west.
The magnitude of this momentum is | mv | and its direction is north-west.
Question T9
If a is a vector and α is a non–zero scalar, classify each of the following statements as always true, always false or sometimes true and sometimes false. Explain your answers.
(a) | α a | cannot be less than zero.
(b) α2 a is in the same direction as a.
(c) −α a is antiparallel to a.
(d) Provided | a | is not zero, $\hat{\boldsymbol a} = \dfrac{{\boldsymbol a}}{\lvert\,{\boldsymbol a}\,\rvert}$ is a vector of unit magnitude in the same direction as a.
(e) $\left\lvert\,\dfrac{{\boldsymbol a}}{\alpha}\,\right\vert = \dfrac{{\boldsymbol a}}{\lvert\,\alpha\,\rvert}$
(f) | α a | = | α | | a |
Answer T9
(a) α a is a vector, so | α a | is the magnitude of a vector. Since any vector magnitude is always a non-negative scalar it follows that | α a | cannot be less than zero, so the given statement is always true.
(b) Whether α is positive or negative, α2 will always be positive so α2 a is always in the same direction as a and the statement is always true.
(c) −α a will be antiparallel to a if α > 0, but it will be parallel to a if α < 0. Thus the given statement is sometimes true and sometimes false.
(d) $\hat{\boldsymbol a} = \dfrac{{\boldsymbol a}}{\lvert\,{\boldsymbol a}\,\rvert}$ may be rewritten as $\hat{\boldsymbol a} = \left(\dfrac{1}{\lvert\,{\boldsymbol a}\,\rvert}\right){\boldsymbol a}$, so it simply represents a vector that has been scaled by the reciprocal of its own magnitude. Since | a | must be a positive quantity $\hat{\boldsymbol a}$ must point in the same direction as a and its magnitude must be $\dfrac{1}{\lvert\,{\boldsymbol a}\,\rvert}\lvert\,{\boldsymbol a}\,\rvert = 1$.
Thus, the given statement is always true. Vectors such as $\hat{\boldsymbol a}$ (vectors of magnitude 1) are called unit vectors and are of great use in more advanced work.
(e) This statement is always false since it equates a scalar (on the left–hand side) with a vector (on the right–hand side).
(f) This statement is always true. It expresses symbolically part of the definition of scaling.
3.2 Adding and subtracting vectors
Two vector quantities of the same type (two displacements say, or two velocities) may be added together to produce another vector quantity of the same type. This operation is called vector addition. It is straightforward, though quite different from the everyday operation of (scalar) addition with which you are familiar.
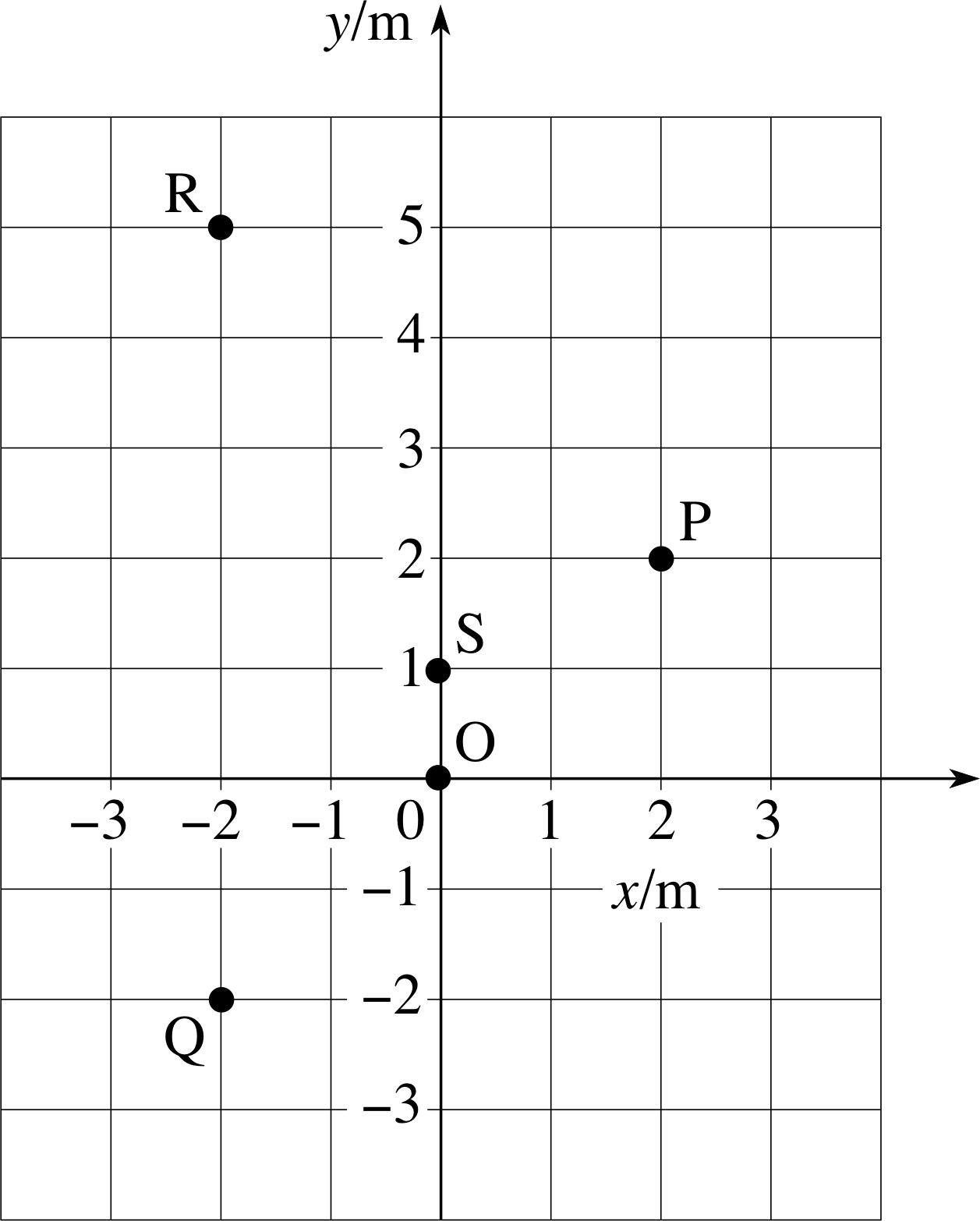
Figure 4 The points O, P, Q, R, S and their locations in the (x, y) plane.
Before examining the general rules for vector addition let’s look at an example to see how the process works in practice. Figure 4 shows the points O, P, Q, R and S that we considered earlier – we shall use these points to provide the example we need. Imagine yourself to be located at Q, the lowest of the five points, and suppose that you undergo a displacement $\overrightarrow{\rm QO}$. Where would you find yourself? Obviously, at O.
Now suppose you undergo another displacement,$\overrightarrow{\rm OS}$. What would your new location be after this second displacement? You would find yourself at point S. So, the overall result of the two successive displacements $\overrightarrow{\rm QO}$ and $\overrightarrow{\rm OS}$ would be to move you from Q to S. But, of course, such an effect could also have been produced by the single displacement $\overrightarrow{\rm QS}$. Thus, it makes sense to write
$\overrightarrow{\rm QO}$ + $\overrightarrow{\rm OS}$ = $\overrightarrow{\rm QS}$(8)
The left–hand side of Equation 8 contains a new kind of quantity – the sum of two vectors. Thus, Equation 8 is an example of vector addition and the vector $\overrightarrow{\rm QS}$ on the right–hand side is said to be the vector sum or resultant_vectorresultant of $\overrightarrow{\rm QO}$ and $\overrightarrow{\rm OS}$.
Question T10
Complete the following (vector) sums. i
(a) $\overrightarrow{\rm OS}$ + $\overrightarrow{\rm SP}$ = (b) $\overrightarrow{\rm PS}$ + $\overrightarrow{\rm SR}$ = (c) ($\overrightarrow{\rm PS}$ + $\overrightarrow{\rm SR}$) + $\overrightarrow{\rm RQ}$ = (d) $\overrightarrow{\rm PS}$ + ($\overrightarrow{\rm SR}$ + $\overrightarrow{\rm RQ}$) =
Answer T10
(a) $\overrightarrow{\rm OS}+\overrightarrow{\rm SP}=\overrightarrow{\rm OP}$
(b) $\overrightarrow{\rm PS}+\overrightarrow{\rm SR}=\overrightarrow{\rm PR}$
(c) $(\overrightarrow{\rm PS} + \overrightarrow{\rm SR}) + \overrightarrow{\rm RQ} = \overrightarrow{\rm PR} + \overrightarrow{\rm RQ} = \overrightarrow{\rm PQ}$
(d) $\overrightarrow{\rm PS} +(\overrightarrow{\rm SR}+\overrightarrow{\rm RQ})=\overrightarrow{\rm PS} + \overrightarrow{\rm SQ}=\overrightarrow{\rm PQ}$
Comment Parts (c) and (d) of this answer show that we may add three (or more) vectors together and that the result does not depend on the order in which the additions are carried out. Thus, it is not at all ambiguous to write PTMS + TMSR + RTMQ without any brackets.
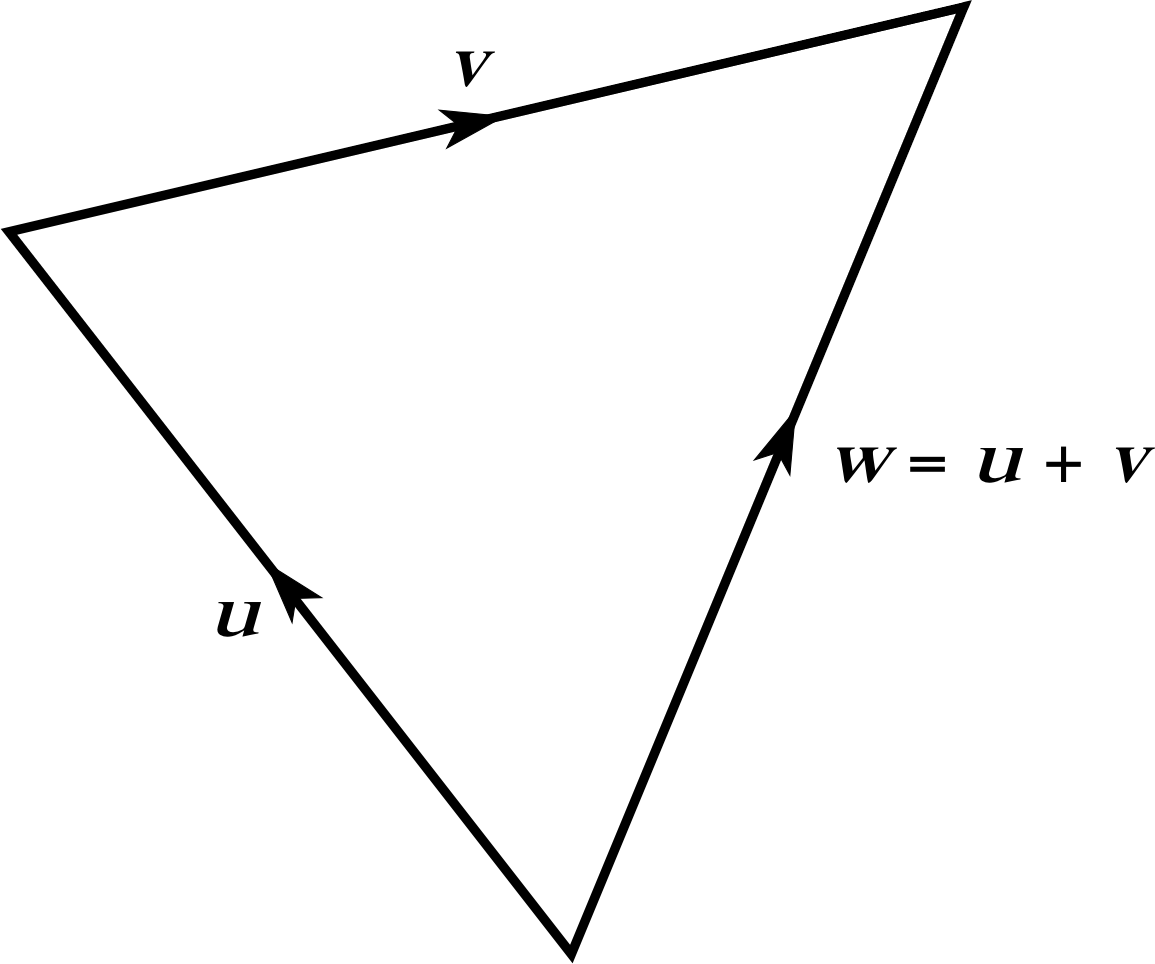
Figure 5 Two vectors, u and v, together with their sum w = u + v.
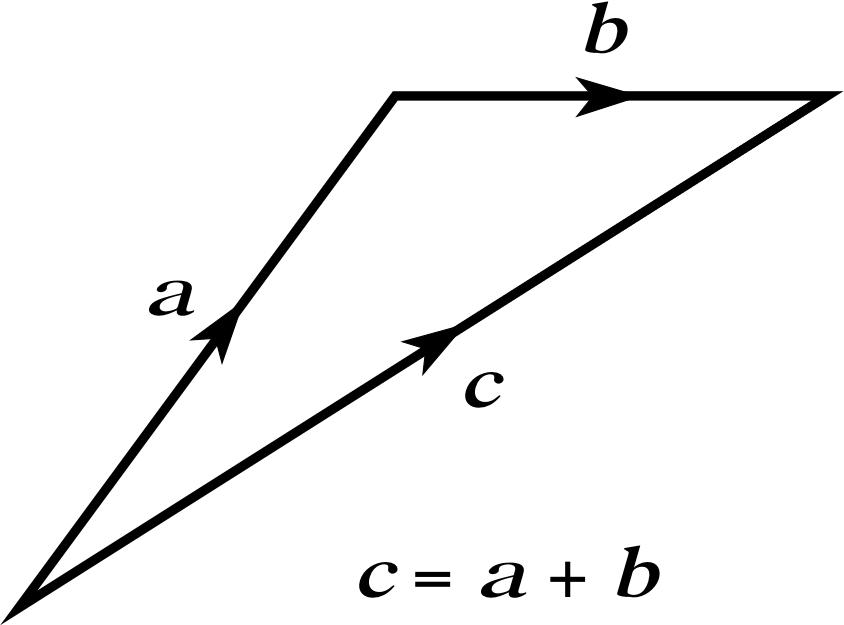
Figure 7 The triangle rule for adding vectors. Note the directions of the arrows; the diagram would be incorrect if any one, or any two of the arrows were reversed.
So far, all the examples of vector addition that we have considered have involved vectors that are ‘nose-to-tail’ like $\overrightarrow{\rm OS}$ and $\overrightarrow{\rm SP}$, but remember, a vector is completely specified by its magnitude and direction; the end–points are immaterial. Points such as O, P, Q, R and S merely provide a convenient way of specifying vectors, the vectors themselves could just as easily be represented by bold–face letters, such as the u and v shown in Figure 5 together with their sum w. Moreover, any vector that has the same magnitude and direction as v is equal to v, irrespective of its endpoints, and could be used in place of v in the equation
u + v = w(9)
Figure 6 shows just such a vector, t. Even though t is shown in a different location from v, the fact that t = v means that it is correct to write:
u + t = w(10)
So, what is the general rule for adding two vectors? The answer is illustrated graphically in Figure 7 and may be summarized in the following triangle rule for vector addition.
The triangle rule for adding vectors:
Let vectors a and b be represented by appropriate arrows (or directed line segments). If the arrow representing b is drawn from the head of the arrow representing a, then an arrow from the tail of a to the head of b represents the vector sum a + b, marked c in Figure 7.
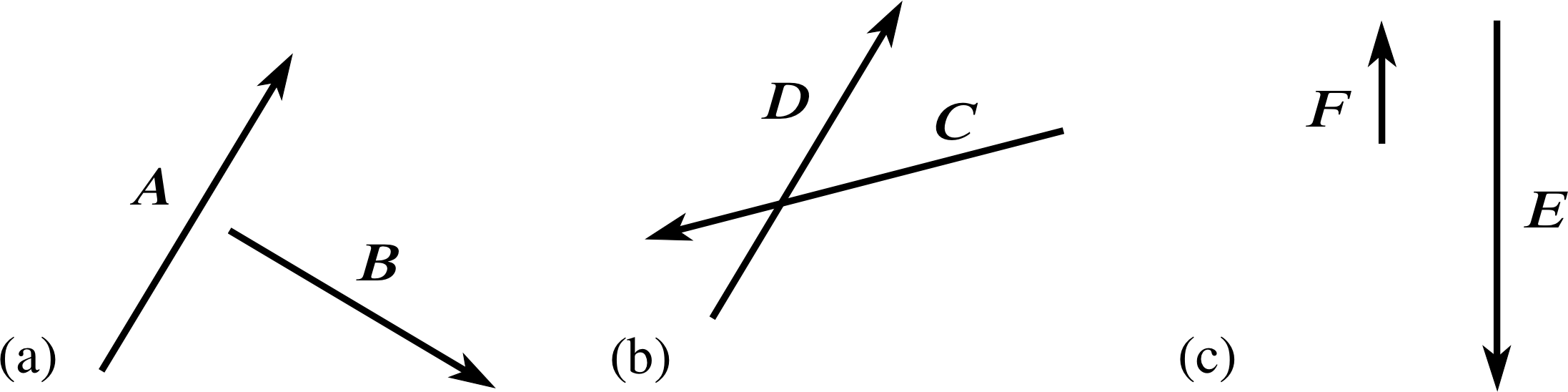
Figure 8 See Question T11.
Question T11
Figure 8 shows three pairs of vectors; A, B; C, D and E, F. Sketch and label some simple diagrams showing how the triangle rule can be used to find the following vector sums:
(a) A + B, (b) C + D, (c) E + F.
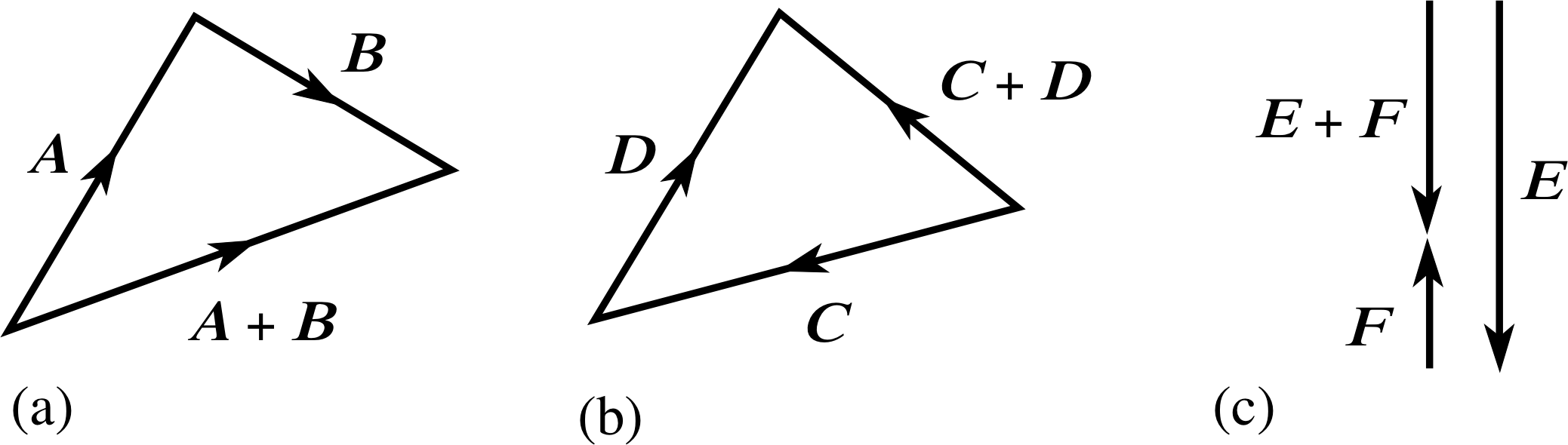
Figure 18 See Question T11.
Answer T11
See Figure 18.
Note that in the case of the vectors E and F the ‘triangle’ has collapsed into a straight line. Nonetheless, the principles of the triangle rule still apply.
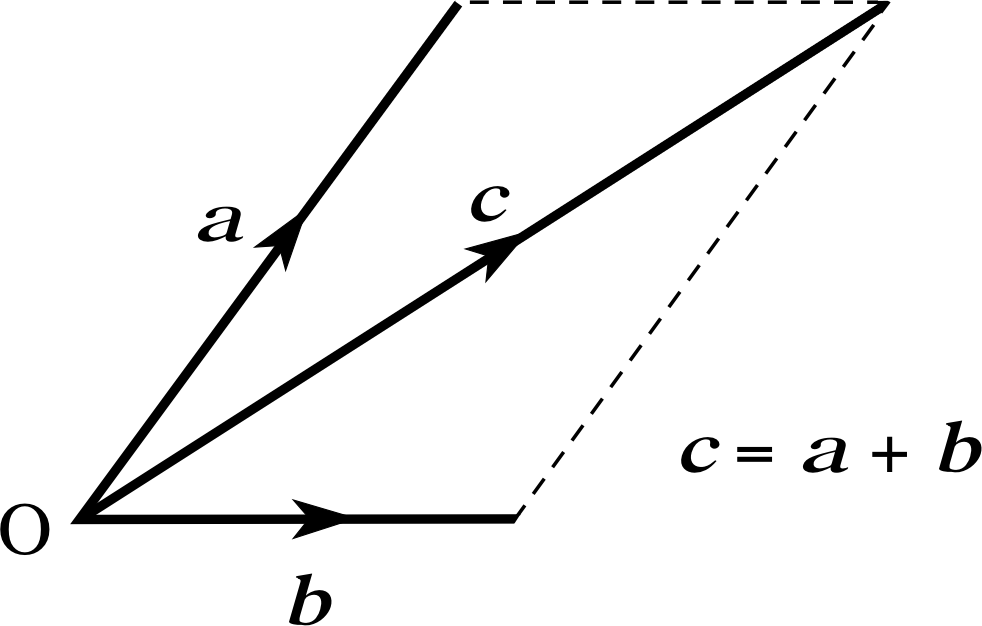
Figure 9 The parallelogram rule for adding vectors.
An alternative but equivalent method of adding vectors graphically is provided by the parallelogram rule. This has no real advantages over the triangle rule, but it is preferred by some authors. It is illustrated in Figure 9 and may be stated as follows.
The parallelogram rule for adding vectors:
Let vectors a and b be represented by appropriate arrows (or directed line segments). If the arrows representing a and b are drawn from a common point O so that they form two sides of a parallelogram, when the parallelogram is completed an arrow from O along the diagonal of the parallelogram represents the vector sum a + b.
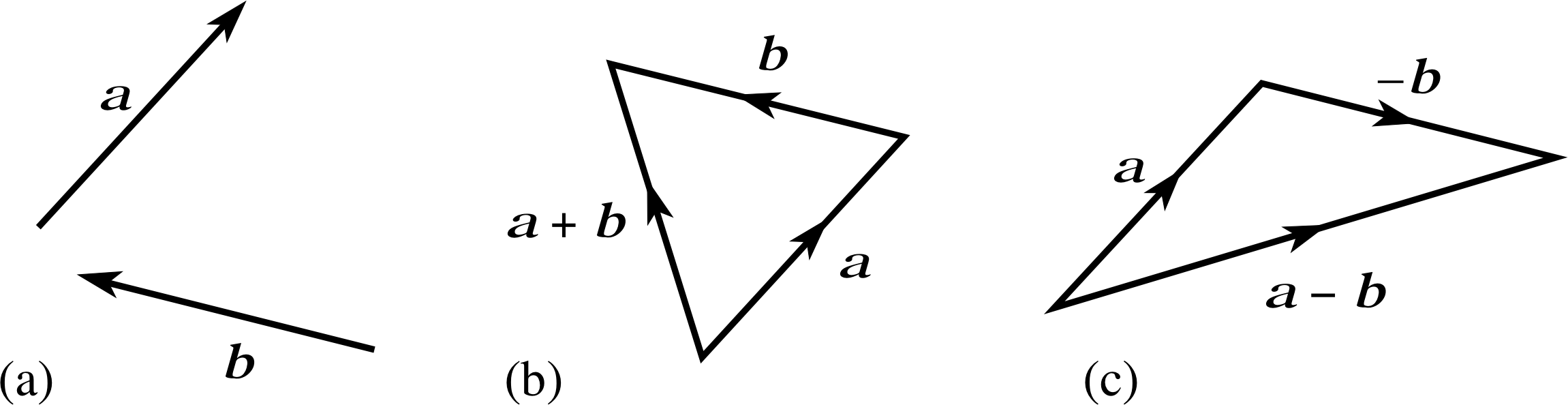
Figure 10 (a) Two vectors, (b) their sum, and (c) their difference.
Despite a lengthy discussion of vector addition, nothing has yet been said about vector subtraction. The time has come to remedy that deficiency.
Given two vectors of the same type, such as the vectors a and b shown in Figure 10a, you already know how to add them together to form their sum a + b (Figure 10b). You also know how to scale the vector b by the number −1 to produce the vector −b that has the same magnitude as b but points in the opposite direction. You should therefore be able to convince yourself that Figure 10c correctly represents the following summation
a + (−1 b)
This quantity is more usually written as
a − b
and is called the vector difference of a and b.
The vector difference a − b of the vectors a and b is the vector sum of a and −1 b.

Figure 8 See Question T12.
Question T12
In Question T11 you were asked to sketch diagrams showing the sums of various pairs of vectors (shown in Figure 8). Now sketch similar diagrams for the differences of the same pairs:
(a) A − B, (b) C − D, (c) E − F.
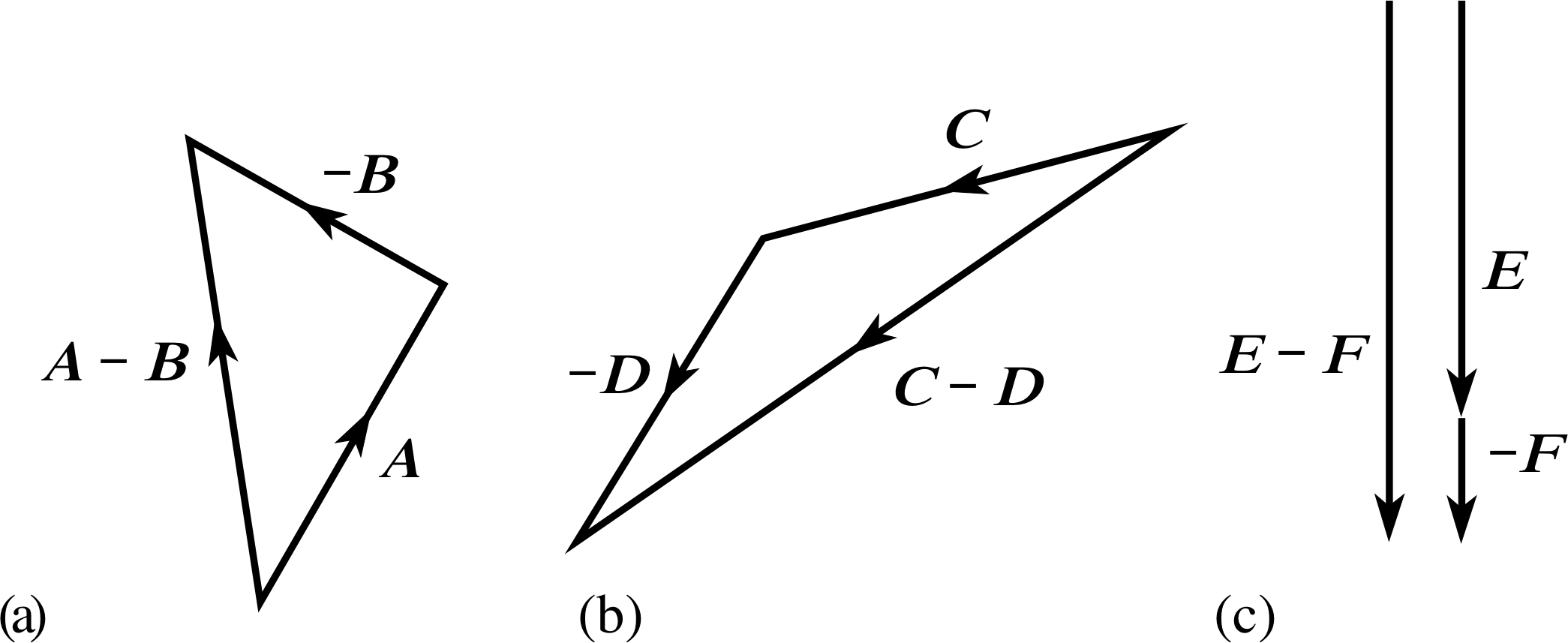
Figure 19 See Question T12.
Answer T12
See Figure 19.
✦ How does the vector A − B in Question T12 differ from the vector B − A?
✧ A − B = − (B − A), so the two vectors have equal magnitude but point in exactly opposite directions.
One final point needs to be discussed before leaving the subject of vector addition and subtraction – the zero vector. It has already been stressed that a vector (which has direction and magnitude) cannot be equal to a scalar (which does not have any direction). However, if we consider the result of a vector subtraction such as a − a it’s obvious that the result has zero magnitude and does not point in any specific direction. So, how should we symbolize this quantity and how should we refer to it? For the sake of consistency we certainly want to call it a vector so it makes sense to dub it the zero vector. As far as its symbolic representation is concerned, different authors take different attitudes. Many simply represent it by 0 as you might expect, but others prefer to use a bold–face zero, 0, to emphasize its vector nature. In FLAP we adopt this somewhat more formal convention, but don’t be surprised if you see the other elsewhere.
✦ The above discussion of the zero vector has not provided a concise definition of 0. Write down an equation that defines the zero vector.
✧ a + 0 = a for any vector a.
Now that you know about the zero vector you should be able to carry out algebraic manipulations with vectors. Try the following exercise.
✦ Rearrange the following vector equation to express c in terms of a and b:
3 a − 4 b + 2 c = 0
✧ Subtracting (3 a − 4 b) from each side gives
(When you are more familiar with vector algebra you should be able to do some of these steps in your head.)
3 a − 4 b + 2 c − (3 a − 4 b) = 0 − (3 a − 4 b)
It follows that, 2 c = 4 b − 3 a
Thus, c = 2 b − $\frac{3}{2}$ a.
Question T13
i An angler sitting on a riverbank is watching a duck paddling across the river. The water in the part of the river in which the duck is paddling is moving at velocity v relative to the angler. The duck is moving at velocity u relative to the water.
(a) What is the velocity of the duck according to the angler?
(b) What is the velocity of the angler according to the duck?
Answer T13
(a) The velocity of the duck relative to the angler will be the vector sum of the duck’s velocity relative to the water and the water’s velocity relative to the angler, i.e. u + v.
(b) The angler’s velocity relative to the duck will be equal in magnitude, but opposite in direction to the duck’s velocity relative to the angler, i.e. −u − v.
3.3 Resolving vectors
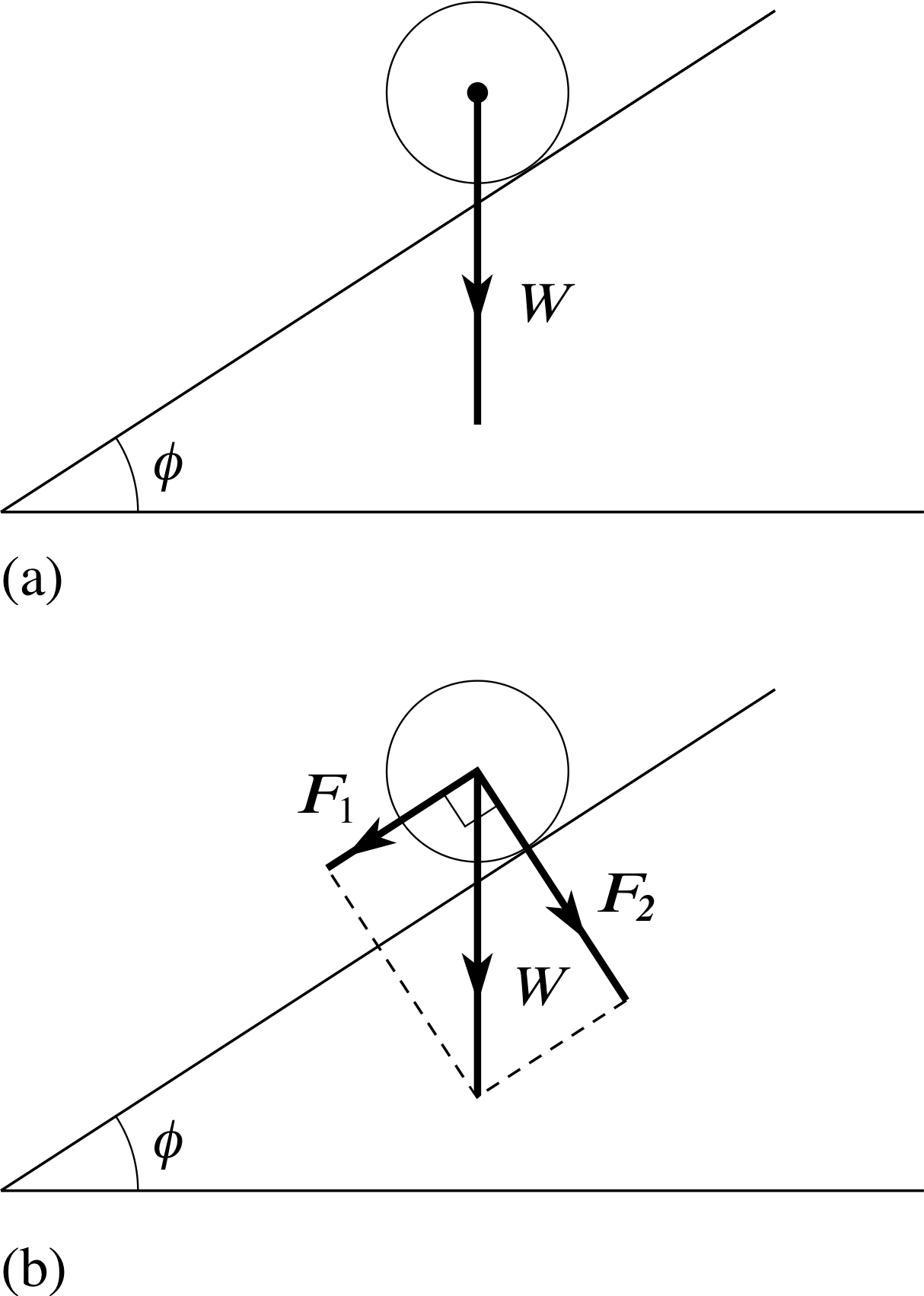
Figure 11 (a) A ball of weight W, released from rest on an inclined plane. (b) The component vectors of W, parallel and normal to the plane.
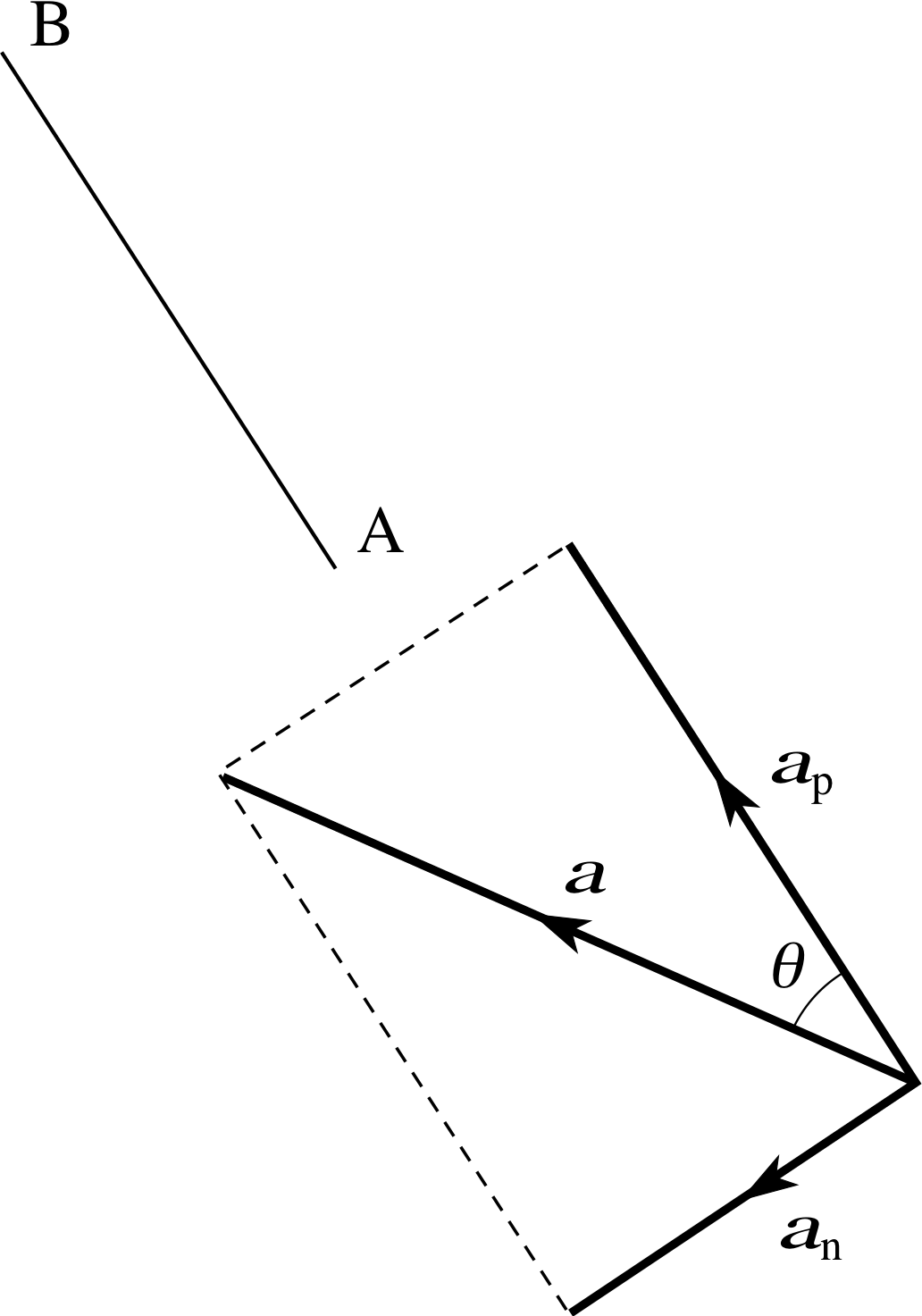
Figure 12 A given vector a and a line AB. The vector is to be resolved into component vectors parallel (ap)and normal (an) to the line AB.
Imagine a ball released from rest on a perfectly smooth inclined plane, as shown in Figure 11a. What will happen to the ball immediately after its release? Obviously, the ball will start to move down the plane, accelerating as it does so. Anyone familiar with Newton’s laws of motion would say that the acceleration of the ball must be caused by a force pointing down the plane. But what is the origin of the force causing that acceleration? The only ‘downward’ force that acts on the ball is its weight, W – the force that arises from the action of gravity on the ball’s mass – and that force acts vertically downwards, not parallel to the plane. So, where does the accelerating force come from?
Happily, vector addition provides a simple answer. The weight W of the ball can be regarded as the sum of two other forces as shown in Figure 11b, and we can write W = F1 + F2. The force F1 that is parallel to the plane causes the acceleration, while the force F2, that is normal (i.e. at right angles) to the plane stops the ball from leaving the plane and accounts for the difference between W and F1. i
This process of splitting a given vector into constituent parts at right angles to each other is called (orthogonal) resolution; we speak of resolving the vector into it’s (orthogonal) component vectors along the chosen directions. The process of orthogonal resolution is not restricted to the directions shown in Figure 11; a vector in a two–dimensional plane can be resolved into orthogonal component vectors along any two mutually perpendicular directions in that plane. (In three dimensions it is always possible to choose three mutually perpendicular directions, and any given vector in three dimensions can be correspondingly resolved into three orthogonal component vectors.
Problems in which a given vector has to be resolved into (orthogonal) component vectors are very common, so it is worth knowing how to perform such resolutions.
The sort of problem you might be asked to solve is illustrated in Figure 12. A vector a is given, and a line AB, inclined at an angle θ to a, is specified. The problem is to resolve a into two component vectors, one parallel to AB, the other normal to AB. To solve the problem, just use the parallelogram rule (in the case of orthogonal component vectors it’s really a ‘rectangle rule’). Construct a rectangle like the one shown in Figure 12, with a as its diagonal and one side parallel to AB. Call the component vectors parallel and normal to AB, respectively, ap and an. Applying basic trigonometry to the rectangle, you should then be able to see that the magnitudes of the two orthogonal component vectors are:
| ap | = | a | cos θ(11) i
and | an | = | a | sin θ(12)
With this information you should be able to find orthogonal component vectors for yourself, though you may need to think carefully about their directions.
Question T14
If the weight of the ball in Figure 11 is of magnitude 5 N and the angle of inclination of the plane (ϕ) is 30°, what are the magnitudes and directions of the orthogonal component vectors F1 and F2? [Hint: Pay attention to the definition of ϕ.]
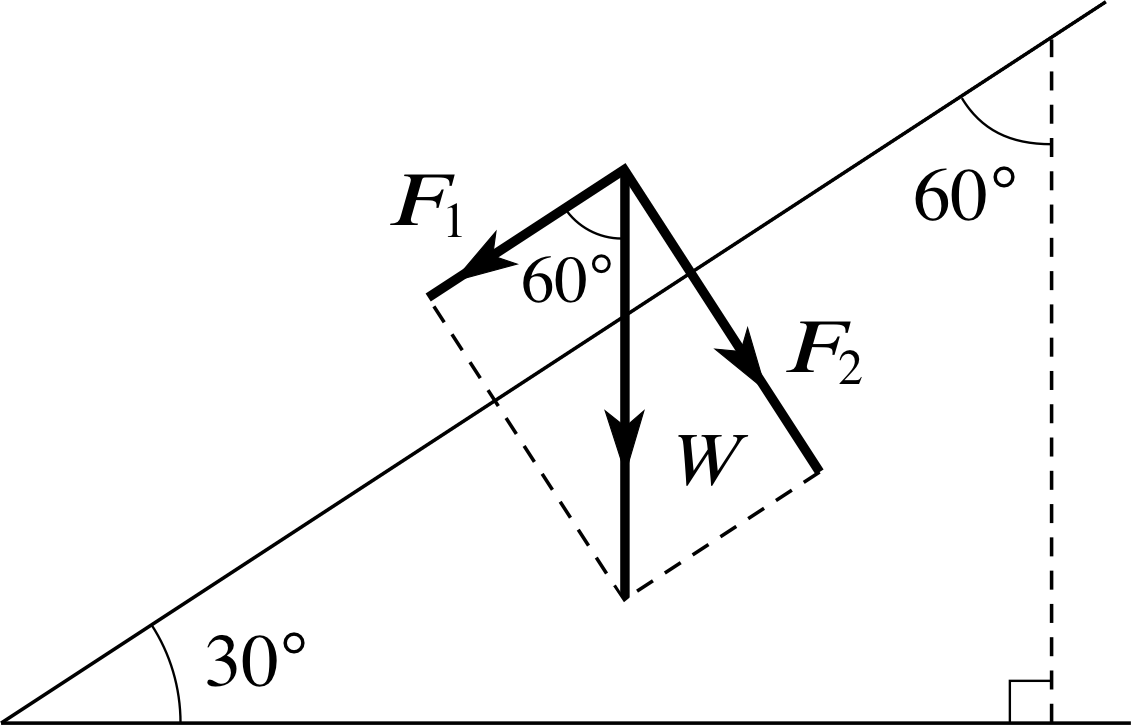
Figure 20 See Question T14.
Answer T14
As you can see in Figure 20,
F1 is at 60° to W. (This is the crucial angle, not the 30° between the plane and the horizontal.) Thus
| F1 | = | W | cos 60° = 2.50 N
| F2 | = | W | sin 60° = 4.33 N
F1 is parallel to the inclined plane in the ‘downhill’ direction.
F2 is normal to the inclined plane, in the downward sense.
(Note that simply saying normal (or parallel) to the plane is ambiguous – you need to specify the upward or downward sense.)
Question T15
An aeroplane is flying along a northwesterly course at 500 km h 1. What are the component vectors of the plane’s velocity parallel and normal to a line running north-south?
Answer T15
The north–west course of the plane means that its velocity is directed 45° to the north–south line. Thus, the orthogonal component vectors of the plane’s velocity, parallel and normal to the line are:
(500 km h−1) cos 45°, due west = 354 km h−1, due west
and(500 km h−1) sin 45°, due north = 354 km h−1, due north.
In principle, the process of resolution is not restricted to situations in which the chosen directions are perpendicular and the component vectors are at right angles to each other. In two dimensions a vector may be resolved into component vectors along any two directions that are not parallel, and in three dimensions a vector may be resolved into component vectors along any three directions that do not all lie in the same plane. The process of carrying out such resolutions is similar to that outlined above, though the mathematics is a little more complicated. Fortunately, such non–orthogonal resolutions are relatively rare in elementary work. It was in order to emphasize this restriction to mutually perpendicular directions that we made such widespread use of the word ‘orthogonal’ in this subsection. However, since orthogonal resolution is so common we do not follow this practice elsewhere in FLAP. Generally speaking, if you are given a vector and asked to find its component vector along some line you should assume that it is the orthogonal component vector along that line which is required unless you are given a clear indication to the contrary.
Important note Pay close attention to the term component vector. As you pursue the study of vectors you will soon encounter scalar quantities referred to as the components of a vector. Like component vectors, these (scalar) components of a given vector can be used to specify that vector. Nonetheless, (scalar) components are different from (though related to) the component vectors we have just been discussing. Take care not to confuse the (scalar) components of a vector with its component vectors. In FLAP the two quantities will always be clearly distinguished, other authors may not be so careful.
4 Working with vectors
The methods that have been used in this module have been largely graphical. Such methods provide a good basis for the introduction of fundamental concepts but they are not well suited to the everyday business of working with vectors. Methods of a more algebraic nature are really needed for that purpose. Such methods exist and are fully developed in other modules of FLAP.
Apart from simplifying calculations, the algebraic methods also have the advantage of making it almost as easy to treat three–dimensional problems involving directions in space as it is to treat two–dimensional problems confined to a plane. The use of vectors in describing and analysing three–dimensional situations makes them one of the most valuable mathematical tools at the disposal of the physicist.
5 Closing items
5.1 Module summary
- 1
-
Subsection 2.1Scalar quantities (or Subsection 2.1scalars) can be completely specified by a single number together with an appropriate unit of measurement.
- 2
-
Subsection 2.2Vector quantities (or Subsection 2.2vectors) can be completely specified by a magnitude and a direction. In diagrams, vectors are usually represented by arrows or directed line segments. In print, vectors are distinguished by bold–face type, and in a manuscript, vectors are indicated by a wavy underline.
- 3
-
The magnitude of a vector is a non–negative scalar that represents the ‘length’ or ‘size’ of that vector. The magnitude of a is shown as | a | in print or | $\underset{\boldsymbol{\raise 6pt \sim}}{a}$ | in a manuscript.
- 4
-
Any vector a may be multiplied by a scalar α to produce a scaled vector α a which points in the same direction as a if α > 0 and in the opposite direction if α < 0. The magnitude of α a is | α a | = | α | | a |.
- 5
-
Vectors may be added graphically using either the triangle rule or the parallelogram rule (Figures 7 and 9).
- 6
-
The zero vector, 0, has the property that a + 0 = a for any vector a.
- 7
-
A vector may be resolved into component vectors along appropriately chosen lines. Given a vector a, its orthogonal component vectors parallel and normal to a line inclined at an angle θ (0° ≤ θ ≤ 90°) to a are of magnitude
| ap | = | a | cos θ
and| an | = | a | sin θ
- 8
-
Displacement, velocity, acceleration, force, weight and momentum are all examples of vector quantities.
5.2 Achievements
Having completed this module you should be able to:
- A1
-
Define the glossary terms introduced in the module – as shown in blue, emboldened and underlined.
- A2
-
Identify unfamiliar quantities as scalars or vectors given the definitions of those quantities and recognize displacement, velocity, acceleration, momentum, force and weight as vector quantities.
- A3
-
Carry out algebraic manipulations with scalar quantities.
- A4
-
Draw diagrams to represent specified vectors in two dimensions using arrows or directed line segments, and determine the magnitude and direction of any vector represented in that way.
- A5
-
Recognize, use and interpret the notations (a,a, | a |, | a |) used to represent vectors and their magnitudes in print and in a manuscript.
- A6
-
Identify violations of vector notation such as equating vectors and scalars or equating vector magnitudes with negative quantities.
- A7
-
Understand and represent graphically the operations of scaling a vector, adding and subtracting vectors and resolving a vector into component vectors in various directions.
- A8
-
Evaluate the magnitudes of the orthogonal component vectors of a given vector parallel and normal to a given line.
- A9
-
Formulate and rearrange simple vector equations including those which involve the zero vector 0.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
Question E1 (A2)
The magnetic field at a point in space (at any particular time) is completely specified by two items of information: (i) A direction. (ii) A non–negative quantity called the strength of the field that can be expressed as some multiple of an SI unit called the tesla (T). Justify the claim that the magnetic field at a point is a vector quantity.
Answer E1
Since the strength of the magnetic field is completely specified by a single number together with an appropriate unit of measurement, it is a scalar. Since, in addition, it is non–negative it satisfies the conditions required of a magnitude. Since the magnetic field at a point is specified by a strength and a direction we can treat it as a vector quantity.
(Reread Subsection 2.1Subsections 2.1 and Subsection 2.22.2 if you had difficulty with this question.)
Question E2 (A2 and A7)
If a number of electrically charged particles are at rest relative to one another in some isolated region of space, and if one of those particles with charge q experiences a force F due to the attraction or repulsion of the others, then we say that the particle is subject to an electric field given by F/q. Is the electric field at the location of the particle a vector quantity? Explain your answer.
Answer E2
Since q is a scalar (as discussed in Question T3) the quantity F/q is a vector. So, if the electric field at a point is given by such a quantity it too must be a vector.
(Reread Subsection 2.2Subsections 2.2 and Subsection 3.13.1 if you had difficulty with this question.)
Question E3 (A4 and A7)
The vectors a and b point north and east, respectively. | a | = 2 cm and | b | = 21 cm. Draw rough sketches to show the following vectors: (a) −$\frac{1}{2}$ a, (b) a − b, (c) 2a + 4b.
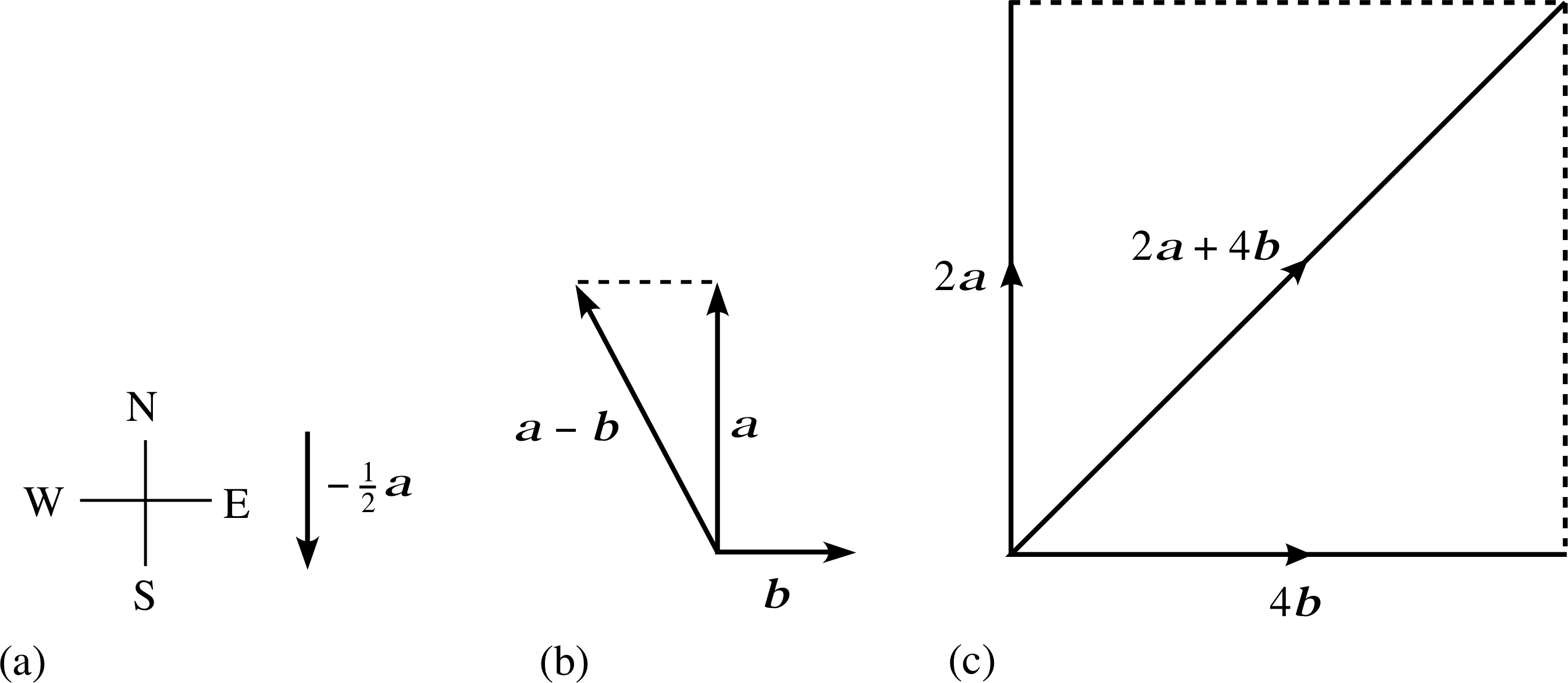
Figure 21 See Question E3.
Answer E3
See Figure 21.
(Reread Subsection 2.2Subsections 2.2, Subsection 2.32.3, Subsection 3.13.1 and Subsection 3.23.2 if you had difficulty with this question.)
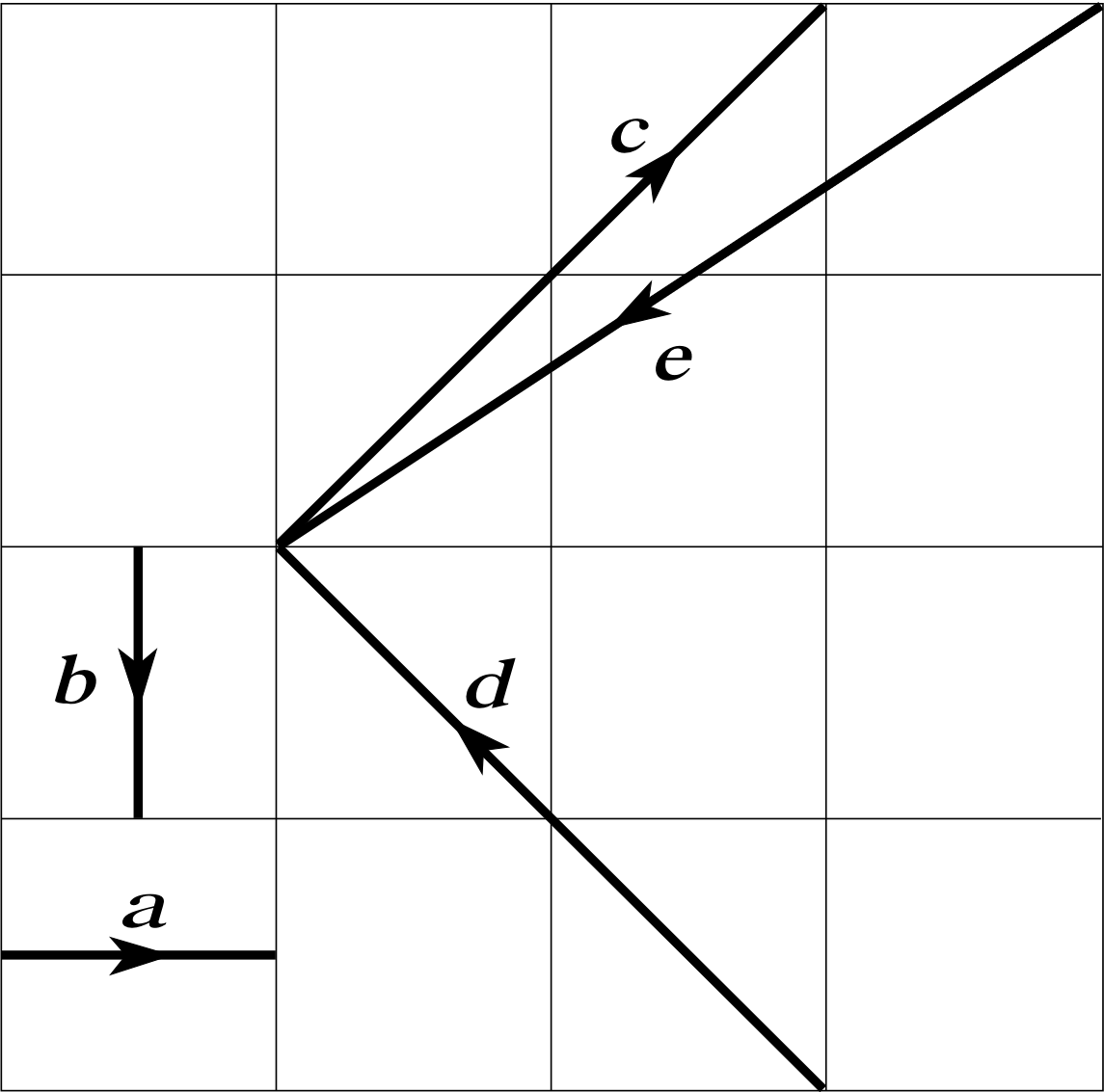
Figure 13 See Question E4.
Question E4 (A4, A7 and A9)
Figure 13 shows five vectors a, b, c, d and e. Express each of the vectors c, d and e in terms of the vectors a and b and hence determine which of the following equations involving those vectors are correct.
(a) c = 2 a + 2 b
(b) −a + 2 b + 2 c + e = 0
(c) −2 a + $\frac{1}{2}$ c + $\frac{1}{2}$ d = 0
Answer E4
By vector addition:
c = 2 a − 2 b
d = −2 a − 2 b
e = −3 a + 2 b
(a) False; c = 2 a − 2 b
(b) True; −a + 2 b + 2 c + e
= −a + 2 b + 2 (2 a − 2 b) − 3 a + 2 b = −a + 2 b + 4 a − 4 b − 3 a + 2 b = 0
(c) False; −2 a + $\frac{1}{2}$ c + $\frac{1}{2}$ d
= −2 a + (a − b) + (−a − b) = −2 a − 2 b
(Reread Subsection 3.1Subsections 3.1 and Subsection 3.23.2 if you had difficulty with this question.)
Question E5 (A4 and A7)
An aircraft has a speed relative to still air of 150 m s−1. The pilot wishes to fly due north when the wind velocity is 20 m s−1 towards the north-east. Draw a sketch showing the compass bearing on which the pilot should fly. Determine the compass bearing to the nearest degree and calculate the speed of the aircraft relative to the ground, correct to one decimal place. [Hint: You might find it useful to recall Question T13.]
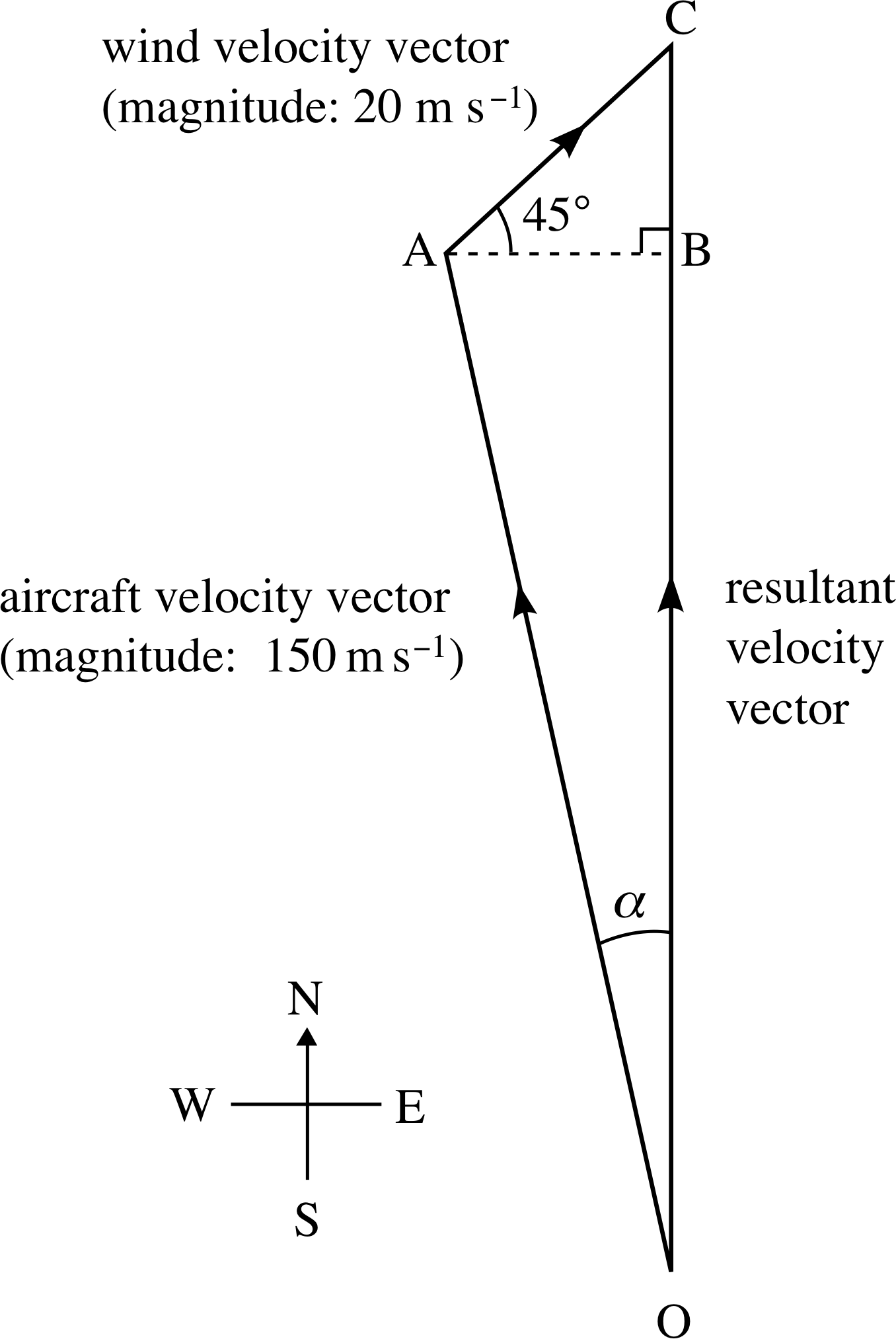
Figure 22 See Question E5.
Answer E5
Your sketch should look something like the diagram in Figure 22 (not to scale).
The required compass bearing is α west of north. To find α note that the length of the line AB in the figure represents a speed of 20 cos 45° m s−1 = 14.14 m s−1. It follows from basic trigonometry that:
$\alpha = \arcsin\left(\dfrac{14.14}{150}\right) = 5.41°$
Thus, the required bearing is 355° (or 5° west of north), (to the nearest degree).
The speed of the aircraft relative to the ground is represented in Figure 22 by the length of the side OC which is the sum of the lengths OB and BC. It follows that the speed is given by:
$\left[\sqrt{\left(150\right)^2 - \left(20\cos 45°\right)^2} + 20\sin 45°\right]\,{\rm m\,s^{-1}}$
= 163.5 m s−1 (to 1 decimal place).
(Reread Subsection 2.2Subsections 2.2, Subsection 2.32.3 and Subsection 3.23.2 if you had difficulty with this question.)
Question E6 (A3, A5 and A6)
If a, b and c are non–zero displacement vectors and α and β are non–zero numbers, classify the following statements as; always true, sometimes true and sometimes false, or always false. Explain your answers.
(a) | α a | = | α | | a |
(b) | a + b | < | a | + | b |
(c) α a = | α a |
(d) α (a + b) = α a + α b
(e) (αβ)(a + b) = α (β a + β b)
(f) (α + β)(a + b) = α a + β b
Answer E6
(a) Always true, a consequence of the definition of scaling.
(b) Sometimes true, but false if a and b are parallel.
(c) Always false, the left–hand side is a vector, the quantity on the right–hand side is a scalar.
(d) Always true, a consequence of the definitions of scaling and (vector) addition.
(e) Always true, (αβ)(a + b) = α [β (a + b)] = α (β a + β b).
(f) Sometimes false, but (α + β)(a + b) = (α + β) a + (α + β) b = α a + α b + β a + β b, and this can equal α a + β b if α b + β a = 0.
(Reread Subsection 2.1Subsections 2.1, Subsection 2.22.2, Subsection 3.13.1 and Subsection 3.23.2 if you had difficulty with this question.)
Question E7 (A1 and A8)
a is a displacement of 30 m, due north. b is a velocity of 20 m s−1, 25° west of north.
(a) What are the orthogonal component vectors of a parallel and normal to b?
(b) What are the orthogonal component vectors of b parallel and normal to a?
(c) Why are you unable to work out the orthogonal component vectors of a + b, parallel and normal to a − b?
Answer E7
(a) The component vector of a parallel to b points 25° west of north and has magnitude (30 m) cos 25° = 27.19 m. The component vector of a normal to b points 65° east of north and has magnitude (30 m) sin 25° = 12.68 m.
(b) The component vector of b parallel to a points due north and has magnitude
(20 m s−1) cos 25° = 18.13 m s−1. The component vector of b normal to a points due west and has magnitude (20 m s−1) sin 25° = 8.45 m s−1.
(c) Neither a + b nor a − b makes any sense, since a and b are different types of vector quantity (their magnitudes are measured in entirely different units). Since it is not possible to define a + b and a − b it is obviously impossible to resolve either of them.
(Reread Subsection 3.3 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.