MATH 2.2: Introducing co–ordinate geometry |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
You probably think of geometry as a subject that involves pictures of points, lines, curves, surfaces and so on; and indeed the origins of the topic are intimately related to the figures that one might draw on a piece of paper. However, if you stick to this classical approach to the subject, you very soon find that the pictures become exceedingly complicated and difficult to visualize; and particularly so in three dimensions. A break–through came in the 17th century when René Descartes (1596–1650) showed that algebraic methods could be applied to geometry, and formulated the subject that we know today as coordinate (or Cartesian) geometry. Of course we continue to use diagrams, but we are no longer bound by them, and most of our arguments are entirely algebraic. You have almost certainly met the idea of a Cartesian coordinate system in school (although you may not have called it that), and so our first task in this module will be to review some of the fundamental ideas. In Sections 2 and 3 we are concerned solely with geometry in two dimensions, but in Section 4 we discuss briefly how some of the ideas can be extended to three dimensions.
The essence of the Cartesian approach to geometry is to specify the position of a point by distances, in mutually perpendicular directions from a given fixed point. In a Cartesian coordinate system two distances are needed to specify the location of a point on a flat surface (known as a plane) and these distances are called coordinates. The given fixed point is called the origin (of coordinates) and the two directions are called axes: one of these is known as the x–axis and the other as the y–axis and the coordinates are written as an ordered pair of numbers. Thus the point represented by the pair (2, 3) has x–coordinate equal to 2 and y–coordinate equal to 3.
Having specified the points in a plane by a Cartesian coordinate system, it is natural to ask how we can determine the distance between two points in terms of their coordinates. We answer this question in Subsection 2.6.
Apart from a point, a straight line is the simplest geometric entity, and we show, in Subsection 2.2 that it can be represented by a simple equation relating values of y for points on the line to corresponding values of x. There is just one equation for a given line, but in Subsection 2.3Subsections 2.3 and Subsection 2.42.4 we will see that this equation can be manipulated into various equivalent forms in order to provide the information that we require.
In Section 3 we take an introductory look at the equation of a circle. In Subsection 3.1 we first derive the equation for a circle with its centre at the origin; then we generalize this equation to cover the cases where the centre is at any point in the plane. In Subsection 3.2 we derive equations for the tangents to a circle, in cases where the tangent passes through a given point outside the circle and in cases where the point of contact on the circle is specified. Subsection 3.3 deals briefly with an important alternative coordinate system – the polar coordinate system.
Section 4 extends some of the earlier results to three dimensions. Subsection 4.1 deals with points in three dimensions and the calculation of the distance between any two of them. Subsection 4.2 presents the equation of a plane surface which has similarities with the general form of the equation of a line in two dimensions. Finally, Subsection 4.3 considers the specification of a line in three dimensions.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to theSubsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 5.1Module summary and the Subsection 5.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 5.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Find the equations of the following straight lines:
(a) the line with gradient −2 and y–intercept 3
(b) the line with gradient 3 passing through the point (−1, 5)
(c) the line through the points (−2, −3) and (−3, 1)
(d) the line with intercepts −1 and 2 on the x– and y–axes, respectively.
Answer F1
(a) y = −2x + 3
(b) y − 5 = 3(x − (−1)), i.e. y = 3x + 8
(c) $\dfrac{y-(-3)}{1-(-3)} = \dfrac{x-(-2)}{-3-(-2)},\text{ i.e. }\dfrac{y+3}{4} = \dfrac{x+2}{-1}$, i.e. $y = -4x-11$
(d) $\dfrac{x}{-1} + \dfrac y2 = 1$, i.e. $y = 2x + 2 $
Question F2
Find the equations of the circles:
(a) centred at the origin and of radius 5
(b) centred at ( −1, −1) and of radius 2
(c) Find the equations of the tangents to the first circle which pass through the point (4, 4)
(d) Find the equation of the tangent to the first circle at the point (−3, 4) on the circle.
Answer F2
(a) x2 + y2 = 25
(b) (x − (−1))2 + (y − (−1))2 = 22
i.e. (x + 1)2 + (y + 1)2 = 4
(c) A line through (4, 4) is of the form
y − 4 = m (x − 4)
i.e.y = mx + (4 − 4m)
and it meets the circle x2 + y2 = 25 where
x2 + [mx + (4 − 4m)]2 = 25
i.e.(1 + m2) x2 + 2m (4 − 4m)x + 16(1 − m)2 − 25 = 0
This quadratic equation has equal roots if
4m2(4 − 4m)2 = 4[16 (1 − m)2 − 25](1 + m2)
Expanding gives us
9m2 + 32m + 9 = 0
Hence$m = \dfrac{16\pm5\sqrt{7\os}}{9}$
The equations of the tangents to the circle through the point (4, 4) are
$y-4 = \left(-\dfrac{16+5\sqrt{7\os}}{9}\right)(x-4)$
and$y-4 = \left(-\dfrac{16-5\sqrt{7\os}}{9}\right)(x-4)$
(d) The tangent to the first circle at the point (x1, y1) on the circle is x1x + y1y = 25
At (−3, 4) this becomes −3x + 4y = 25.
Question F3
(a) What is the distance between the points (1, 2, 3) and (−1, 3, −2)?
(b) Write down the equations which determine the line joining these points.
(c) Does this line lie in the plane x − 3y − z = −8?
Answer F3
(a) From Equation 16, the distance is found to be
$\sqrt{\smash[b]{[1-(-1)]^2+(2-3)^2+[3-(-2)]^2}} = \sqrt{\smash[b]{2^2+(-1)^2+5^2}} = \sqrt{30\os}$
(b) Using Equation 20 we can write down the equations
$\dfrac{x-1}{l} + \dfrac{y-2}{m} + \dfrac{z-3}{n}$
But the point (−1, 3, −2) also lies on the line, therefore
$\dfrac{-1-1}{l} + \dfrac{3-2}{m} + \dfrac{-2-3}{n}\text{ i.e }\dfrac{-2}{l} = \dfrac1m = \dfrac{-5}{n}$
Therefore l = − 2; m = 1; n = −5.
The following equations therefore determine the line
$\dfrac{x-1}{-2} + \dfrac{y-2}{1} + \dfrac{z-3}{-5}$
(c) The point (1, 2, 3) lies in the plane x − 3y − z = −8 (because 1 − 6 − 3 = −8) as does the point (−1, 3, −2) (because −1 − 9 + 2 = −8).
Since both points lie on the plane so does the line joining them.
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with the following terms: circle, dimensions, distance, equation, function, intersection, inverse trigonometric functions (arcsin (x), arccos (x) and arctan (x)), i line, modulus | x |, plane, point, simultaneous equations, tangent_to_a_curvetangent line, trigonometric ratios and variable. You will need to be proficient in manipulating algebra and be able to apply Pythagoras’s theorem (and its converse); and you will also need to be able to find the area of a triangle, and to solve quadratic equations and state the condition that ensures that such equations have two real roots. In addition, you will need to be familiar with SI units. One question requires the use of certain trigonometric identities, but these are provided in the text. If you are uncertain of any of these terms you can review them now by referring to the Glossary which will indicate where in FLAP they are developed. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Note that in this module $\sqrt{x\os}$ means the positive square root of the non–negative number x.
Question R1
Which of the following are correct statements?
(a) (x − 1)(y − 2) − 3(x − 5)(y − 4) − 12 = −2(x − 7)(y − 5) for all values of x and y.
(b) $\dfrac{3a + b}{a} = 3 + b$ for all values of a and b.
(c) The quadratic equation x2 + 2x + 1 = 5 has just one real root.
(d) (m2 + 3m + 2)2 = m4 + 9m2 + 4 for all values of m.
Answer R1
(a) True. If we expand the equation we find
(x − 1)(y − 2) − 3(x − 5)(y − 4) − 12 = −2xy + 10x + 14y − 70 = −2(x − 7)(y − 5)
(b) False.
(c) False.
(d) False.
If you got any part of this question wrong then you need some extra help with elementary algebra, and you should consult your tutor.
Question R2
If two sides of a right–angle triangle are 5 m and 12 m, does it follow that the third side is 13 m?
Answer R2
This is only true if the unknown side is the hypotenuse. If the side of length 12 m is the hypotenuse then the remaining side will be $\sqrt{119\os}$ m.
Consult Pythagoras’s theorem in the Glossary for further information.
Question R3
What is the definition of a circle?
Answer R3
A circle is a curve, lying in a plane, every point of which is equidistant from a given point. (Not the apocryphal schoolboy definition ‘a straight round line, with a hole in the middle’.)
Consult circle in the Glossary for further information.
Question R4
What does it mean to say that ‘a line is a tangent to a circle’?
Answer R4
A tangent is the line that meets the circle at one point only.
Consult tangent_to_a_curvetangent in the Glossary for further information.
2 Straight lines
2.1 Cartesian coordinates
The framework that we use to draw pictures of curves is provided by a Cartesian coordinate system, consisting of a pair of straight lines at right angles, called coordinate axes, as shown in Figure 1. The two lines are infinitely long, but we draw only a portion of each near the point where they cross, which is known as the origin. The horizontal line is called the x–axis and the vertical line the y–axis, and both lines are scaled to indicate distance from the origin along the line. Distances to the right of the origin along the x–axis are positive while those to the left are negative; along the y–axis, distances above the origin are positive while those below are negative. It is usual to place arrowheads on the axes to show the direction of increasing x and y (since occasionally we may wish to change the orientation of the axes).
Any pair of values for x and y can be used to determine a point in the coordinate system. Thus, for example, the ordered pair (2, 1) is shown as the point A in Figure 1; a vertical line from A to the x–axis meets it at x = 2, while a horizontal line from A to the y–axis meets it at y = 1. Similarly, the points B and C in Figure 1 represent the ordered pairs of numbers (1, 1) and (−1, 2), respectively.
✦ What can you say about the coordinates of a point: (a) on the x–axis, (b) on the y–axis?
✧ (a) y is zero on the x–axis, and the point is of the form (x, 0),
(b) x is zero on the y–axis, and the point is of the form (0, y).
Question T1
Which values of (x, y) correspond to the points D, E, F, G, O in Figure 1?
Answer T1
D is (−2, 1), E is (−2, −2), F is (−1, −1), G is (1, −2) and O is (0, 0), this is the origin.
The points where a given line crosses the x– and y–axes are known as the x– and y–intercepts, respectively (although some authors refer to the y- intercept as the intercept).
2.2 Equation of a straight line - gradient and y–intercept
| x | y |
|---|---|
| −3 | −5 |
| −2 | −2 |
| −1 | −1 |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
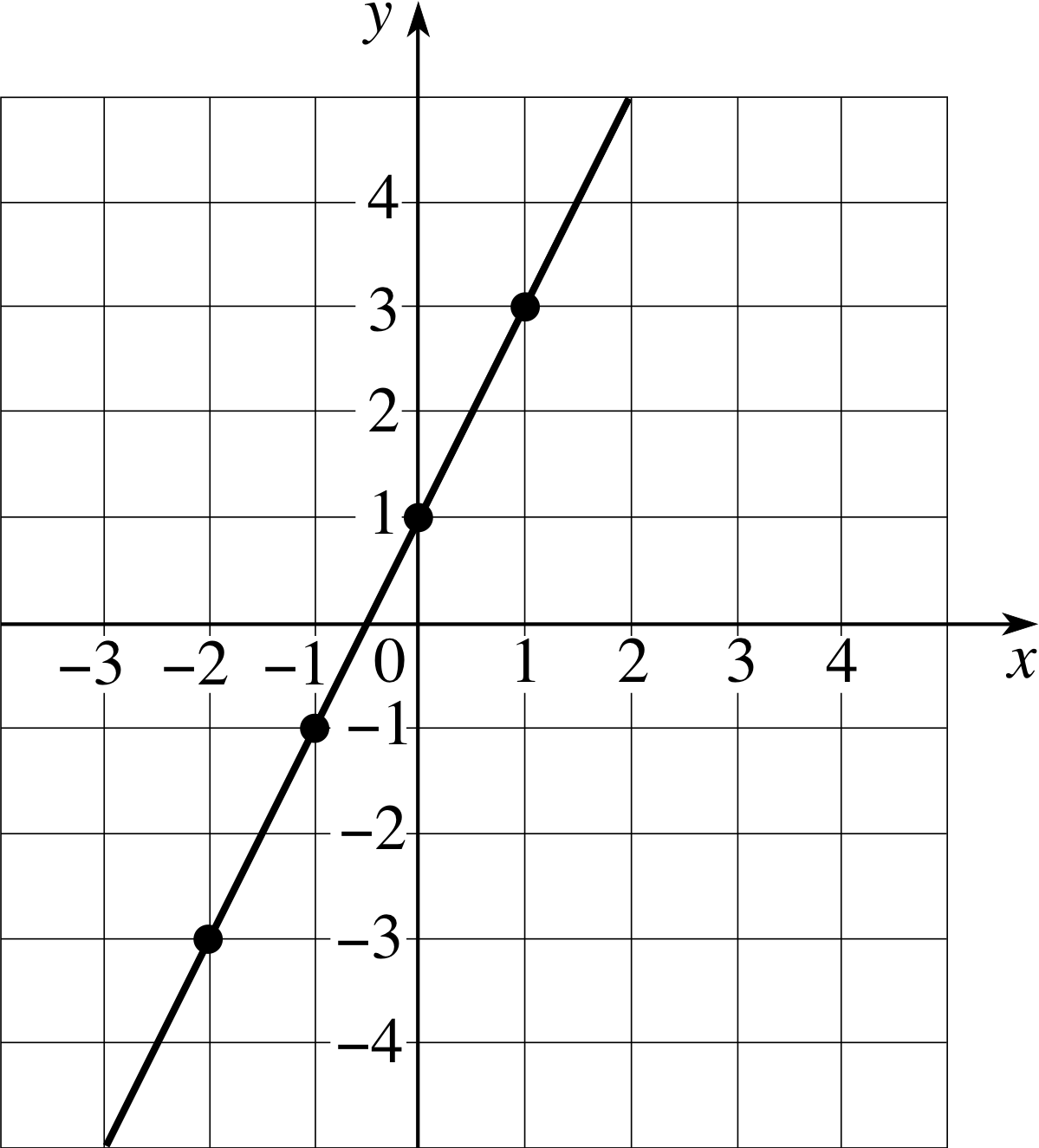
Figure 2 The graph of y = 2x + 1.
A linear function is a function of the form f (x) = mx + c where m and c are constants. For example, f (x) = 2x + 1 when m = 2 and c = 1, and, if we let y denote the values of f (x), we may plot the graph of y = 2x + 1 as in Figure 2. It should come as no surprise that the graph is a straight line; this is after all why such functions are called linear.
You may have used a table of values (as in Table 1) to construct such a graph.
In fact, once you know that the graph must be a straight line, it is quite unnecessary to tabulate all these values. You just need to know two well spaced points, such as (−3, −5) and (3, 7), then join them with a straight line (although it is wise to calculate a third point and check that it lies on the line that you have drawn).
It is essential to realize that the equation y = 2x + 1 is a true statement if, and only if, we choose a point (x, y) that lies on the line. For example, the values x = 2.5 and y = 6 correspond to the point (2.5, 6) which lies on the line because 6 = 2 × 2.5 + 1; on the other hand, the point (3.5, 7) does not lie on the line because 7 ≠ 2 × 3.5 + 1. i (Notice that we do not need to draw the graph in order to reach these conclusions.)
✦ Do the following points lie on the line y = 2x + 1:
(a) (0.5, 2) (b) (989.13, 1979.26) (c) (0.0013, 1.0025)?
✧ (a) From Figure 2 we can see that the point (0.5, 2) lies on the graph. Alternatively, we can be sure that this is so because
$\underbrace{2}_{\color{purple}{\large y}} = 2 \times \underbrace{0.5}_{\color{purple}{\large x}} + 1$.
(b) $\underbrace{1979. 26}_{\color{purple}{\large y}} = 2 \times \underbrace{989.13}_{\color{purple}{\large x}} + 1$ and therefore the point (989.13, 1979.26) lies on the line.
(c) $\underbrace{1. 0025}_{\color{purple}{\large y}} \ne 2 \times \underbrace{0. 0013}_{\color{purple}{\large x}} + 1$ so that the point (0.0013, 1.0025) does not lie on the line. i
The two constants, m and c, which characterize a linear function are called the gradient (or sometimes the slope) and the y–intercept, respectively. i
Look again at Figure 2. Note that the straight line y = 2x + 1 crosses the y–axis at the point where y = 1, which is the value of c (i.e. the y–intercept). Also, from Table 1, we see that a unit increase in the value of x gives rise to an increase of two units in the value of y. This factor of 2 corresponds to the value of m, the gradient of the linear function, and, in graphical terms, it is this value that determines how steep the line will be. In the case of m = 2, one step to the right implies two steps up. i
The gradient–intercept form of the equation of a straight line is
$y = \underbrace{m}_{\color{purple}{\large\text{gradient}}} x + \underbrace{c}_{\color{purple}{\large{y-\text{intercept}}}}$(Eqn 1)
where m and c are constants.
✦ Sketch the straight lines corresponding to the following:
(a) m = 1 and c = 0, (b) m = 0 and c = 1
✧ (a) This corresponds to the equation y = x, and is a straight line through the points E, F and B in Figure 1. (Note that the line goes through the origin since c = 0).
(b) This corresponds to the equation y = 1, and is a straight line through the points D, B and A in Figure 1. (Note that the line is horizontal since the gradient is zero.)
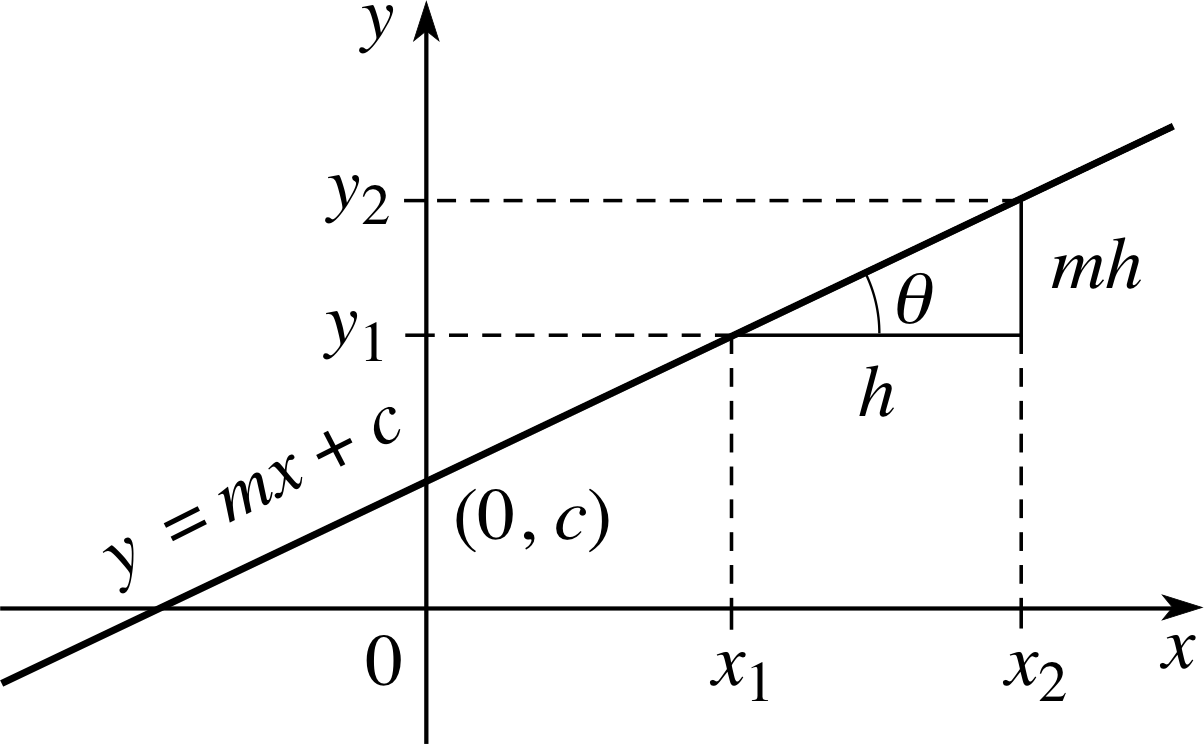
Figure 3 The gradient–intercept form of the straight line y = mx + c.
Figure 3 represents an arbitrary line with equation y = mx + c. The constant c is known as the y–intercept because the point (0, c) on the y–axis lies on this line.
Suppose now that (x1, y1) and (x2, y2) are any two points lying on the line, then
y1 = mx1 + c
andy2 = mx2 + c
Subtracting these equations we have
y2 − y1 = mx2 − mx1
and it follows that $m = \dfrac{y_2-y_1}{x_2-x_1}$(2)
If we let x2 − x1 = h, as in Figure 3, then y2 − y1 = mh and tan θ = m.
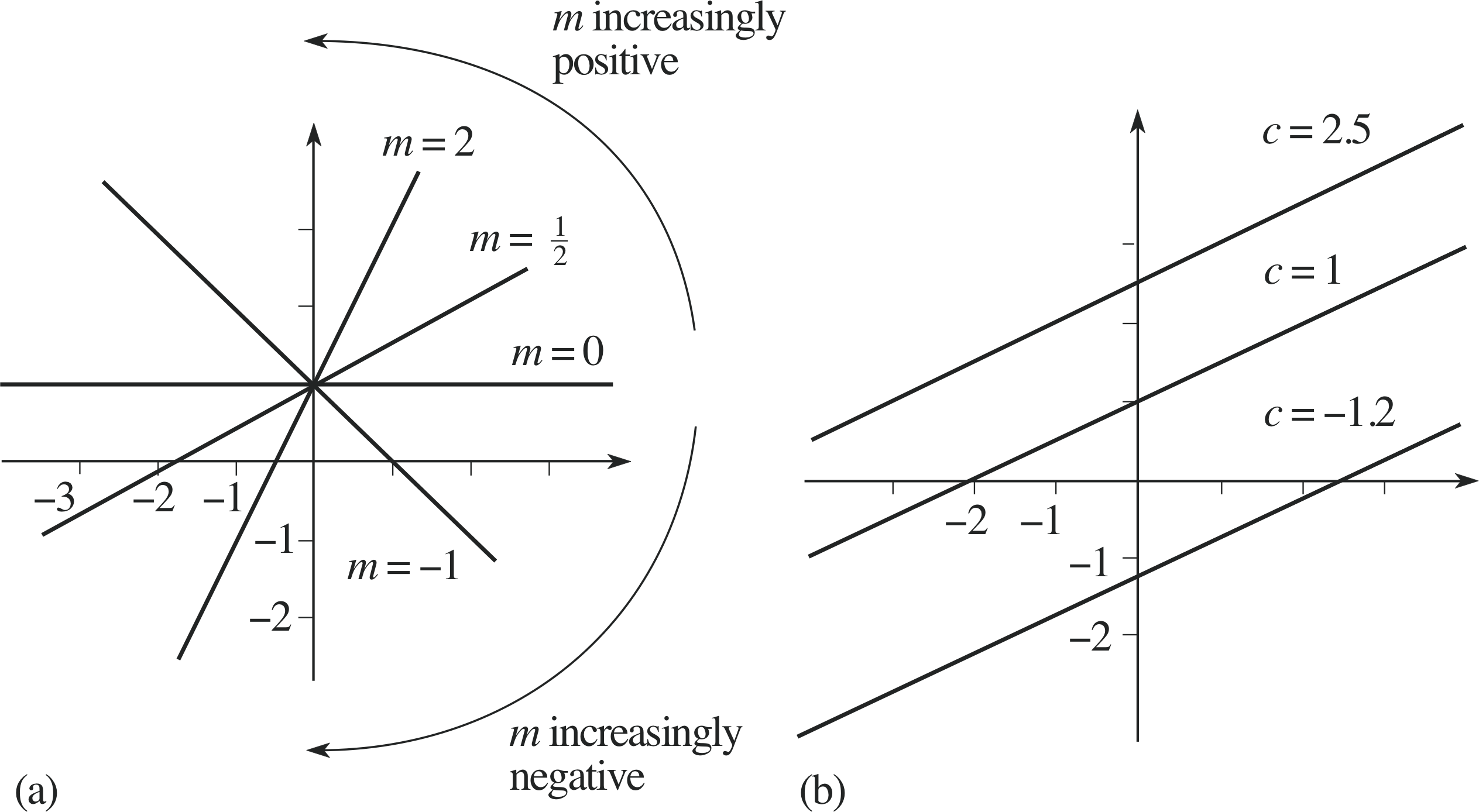
Figure 4 (a) Varying the gradient m, (b) varying the intercept c.
Figures 4a and 4b show, respectively, the effects on the line of different values of m and of c.
Varying the value of m, and keeping c fixed, will rotate the line about a fixed point (the intercept) on the y–axis. If m is positive then the graph slopes upwards from left to right, whereas if m is negative then the graph slopes downwards from left to right. Note that the graph is horizontal when m = 0.
Varying the value of c, and keeping m fixed, produces lines with the same gradient (they are parallel to one–another). If c = 0 the line passes through the origin; increasing c raises the line, while decreasing c lowers it.
✦ What is the gradient of the line that passes through the points (−1.3, 2.8) and (−3.4, 1.2)?
✧ Let x1 = −1.3, y1 = 2.8 and x2 = −3.4, y2 = 1.2 then (using Equation 2) we have
$m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{1.2-2.8}{-3.4-(-1.3)} = \dfrac{-1.6}{-2.1} = 0.762$ i
✦ What is the gradient–intercept equation of the line that passes through the points (−1.3, 2.8) and (−3.4, 1.2)?
✧ The equation of the line is y = mx + c, and from the previous question we know that m ≈ 0.762, but we also know that the point (−1.3, 2.8) lies on the line, so that 2.8 = m (−1.3) + c and substituting the known value for m we have 2.8 ≈ 0.762 × (−1.3) + c which gives c ≈ 3.791; thus the equation of the line is (approximately) y = 0.762x + 3.791.
Equations of lines need not be in gradient–intercept form, for example the equation x = 5y + 3 represents a line, but its gradient and y–intercept are not immediately obvious. However, if we rearrange this equation into the form $y = \dfrac15x - \dfrac35$ it becomes clear that the gradient is 1/5 while the y–intercept is −3/5.
Question T2
What are the gradients and y–intercepts of the following lines?
(a) y = 2 − x/3, (b) 2y = 4x − 5, (c) 2x + 3y = 5, (d) y = 3(x − 1), (e) $\dfrac{y-3}{x+2}=1$, (f) $\dfrac{2}{x-1} = \dfrac{1}{y+3}$
Answer T2
(a) Equation can be rearranged to $y = -\dfrac13x + 2$ so that m = −1/3 and c = 2
(b) y = 2x − 2.5 so that m = 2 and c = −2.5
(c) $y=-\dfrac23x+\dfrac53$ so that m = −2/3 and c = 5/3
(d) y = 3x − 3 so that m = 3 and c = −3
(e) y = x + 5 so that m = 1 and c = 5
(f) $y = \dfrac12x-\dfrac72$ so that m = 1/2 and c = −7/2
2.3 Straight line with a given gradient through a given point
Suppose that we wish to find the equation of the line through the point (1, −2) with gradient 0.5. We know the gradient, so the equation must be of the form
y = 0.5x + c
and it remains to find the value of c. Using the fact that the point (1, −2) lies on the line we have −2 = 0.5 + c from which it follows that c = −2.5, and so the required equation is y = 0.5x − 2.5.
Alternatively, we could use Equation 2, letting the known point (1, −2) be the first point on the line, and an arbitrary point (x, y) on the line be the second, then
$0.5 = \dfrac{y-(-2)}{x-1}$
which can be rearranged to give y = 0.5x − 2.5 as before.
To obtain a general formula we can let the given point have coordinates (x1, y1) and let the gradient of the line be m, then for an arbitrary point (x, y) on the line, using Equation 2, we have $m = \dfrac{y-y_1}{x-x_1}$ which can be rearranged into
The point–gradient form of the equation of a straight line
y − y1 = m (x − x1)(3)
i.e. y = mx + y1 − mx1, from which it is easy to see that the y–intercept is y1 − mx1. i
✦ Given that a line has gradient −5 and passes through the point (1, 3) use the following methods to find its equation:
(a) by finding the value of c in the equation y = mx + c
(b) and then by using Equation 2.
✧ (a) We know that y = −5x + c and, since (1, 3) lies on the line, 3 = (−5) × 1 + c so that c = 8, and the equation is y = −5x + 8.
(b) From Equation 2 we have $-5 = \dfrac{y-3}{x-1}$ which can be rearranged to give y = −5x + 8.
While it is quite acceptable to find the equation of the line by calculating the value of c, it is perhaps slightly easier to use Equation 2.
$m = \dfrac{y_2-y_1}{x_2-x_1}$(Eqn 2)
✦ What is the equation of the straight line through the point (−1, −2) with gradient 3?
✧ From Equation 2 we have $3 = \dfrac{y-(-2)}{x-(-1)}$ which can be rearranged to give y = 3x + 1.
Question T3
The equation $5 = \dfrac{y +2}{x-1}$ is the equation of a line.
(a) What is the gradient of the line?
(b) Does the line pass through the point (−1, 2)?
(c) What is the equation of this line in gradient–intercept form?
(d) What is the y–intercept of this line?
Answer T3
(a) The equation is the same form as Equation 2, so the gradient is clearly 5.
(b) The line does not pass through (−1, 2) (but it does pass through (1, −2)).
(c) The equation in gradient–intercept form is y = 5x − 7.
(d) The y–intercept is −7.
2.4 Other forms of the equation for a straight line
Given two points on the line
Suppose that we are given two points, say (2, −5) and (7, 3), and that we are asked to construct the equation of the line joining them. A straightforward method would be to first use Equation 2 to find the gradient, and then to find c, the y–intercept. From Equation 2 we have
$m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{3-(-5)}{7-2} = \dfrac85$
If the equation of the line is y = mx + c, and using either one of the points on the line, (7, 3) say, we have $3 = \dfrac85 \times 7 + c$ so that c = −41/5.
Finally we can write the equation of the line as $y = \dfrac85x - \dfrac{41}{5}$
The above method is quite acceptable, but it is slightly easier to use Equation 2 twice.
First we find the gradient of the line to be 8/5 as before, but then we choose an arbitrary point (x, y) on the line, and use Equation 2 again with say (7, 3) as the first point and (x, y) as the second, which gives
$m = \dfrac{y-3}{x-7}$
Since we know the value of m to be 8/5, this gives
$\dfrac85 = \dfrac{y-3}{x-7}$
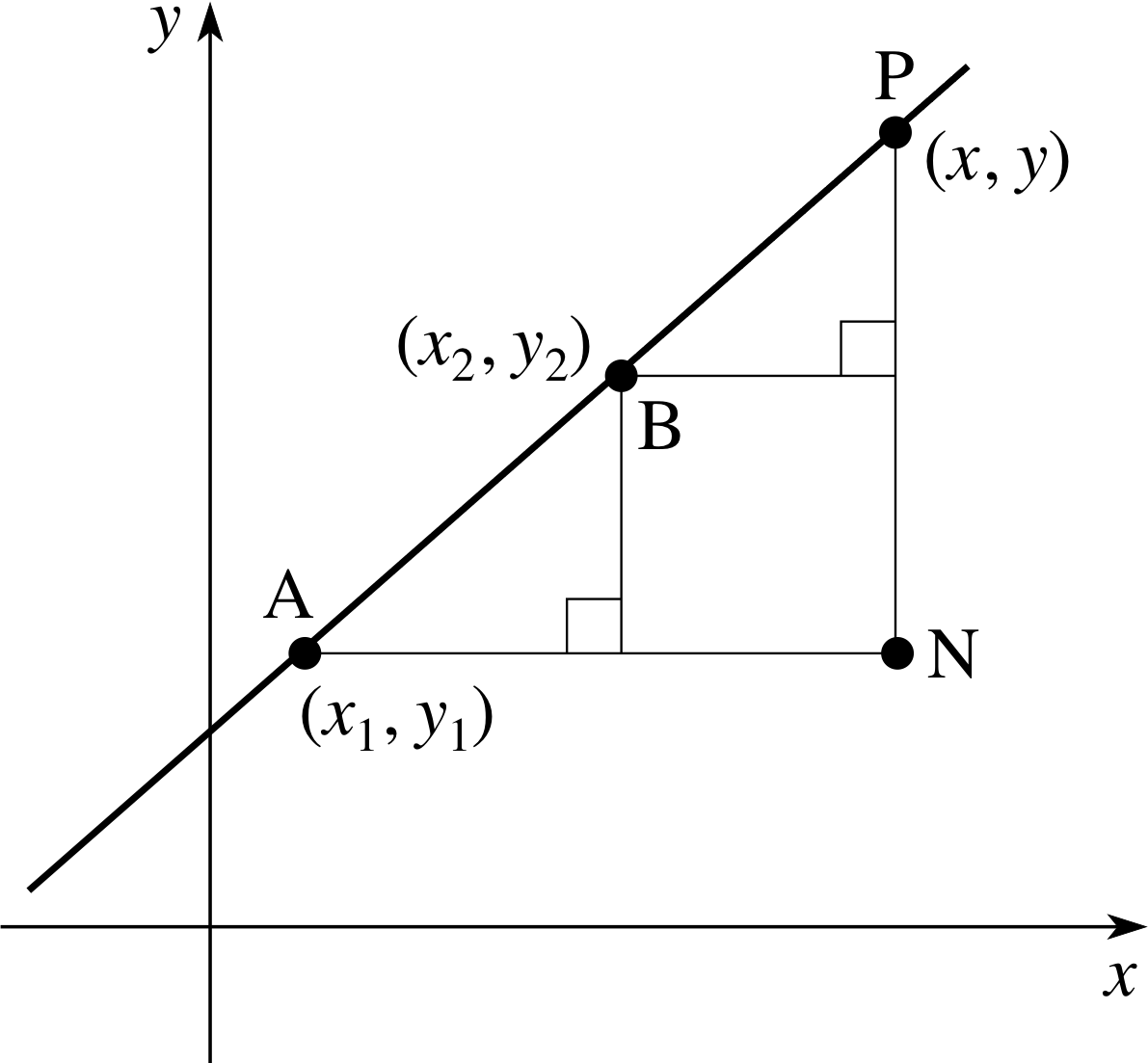
Figure 5 Graph of a straight line through two given points.
which can be rearranged to give $y = \dfrac85x - \dfrac{41}{5}$.
We will now generalize this result, using the second of these methods.
Let the coordinates of two given points A and B be (x1, y1) and (x2, y2) respectively, i and let P(x, y) be a general point on the line, as in Figure 5.
Using Equation 2 and the coordinates of points A and B we have
$m = \dfrac{y_2-y_1}{x_2-x_1}$
but using Equation 2 with the coordinates of points A and P gives us
$m = \dfrac{y-y_1}{x-x_1}$
Therefore equating these two expressions for m gives us
The two–point form of the equation of a straight line
$\dfrac{y-y_1}{x-x_1} = \dfrac{y_2-y_1}{x_2-x_1}$(4) i
✦ Find the equation of the straight line passing through the points A(2, 5), and B(−1, 3).
✧ $\dfrac{y-5}{x-2} = \dfrac{3-5}{-1-2} = \dfrac{-2}{-3} = \dfrac23$
so that$y = \dfrac23(x-2)$
i.e.$y = \dfrac23x -\dfrac43 +5$
or$y = \dfrac23x+\dfrac{11}{3}$
In physics we are often confronted with relationships which are certainly not linear, for example the periodic time T for small vibrations of a simple pendulum is given by the formula $T=2\pi\sqrt{l/g\os}$ where l is the length of the pendulum and g is the magnitude of the acceleration due to gravity.
Such equations can sometimes be simplified by a change of variable, and in this case if we let y = T and x = l then the equation becomes $y = (2\pi/\sqrt{g\os})x$ which is the equation of a line through the origin with gradient $2\pi/\sqrt{g\os}$.
Such an expression could form the basis for an experiment to determine the value of g. We could perhaps vary the length l of the pendulum and measure the corresponding times T, then plot y against x and measure the gradient. Once we have estimated this value it would be then a simple matter to estimate the value of g, as the following exercise shows.
✦ In the experiment described above only two measurements were made (allowing 10 cycles of the pendulum in each case) giving the following values.
T = 1.4 s when l = 0.5 m, and T = 1.7 s when l = 0.75 m.
Fit a straight line to the data in the manner described above, and hence estimate the value of g.
✧ If we let $x_1 = \sqrt{0.5\os}\,{\rm m}^{1/2}\text{, }y_1 = 1.4\,{\rm s}\text{ and }x_2 = \sqrt{0.75\os}\,{\rm m}^{1/2}\text{, }y_2 = 1.7\,{\rm s}$ then using Equation 4 we have
$\dfrac{y-(1.4\,{\rm s})}{x-(\sqrt{0.5\os}\,{\rm m}^{1/2})} = \dfrac{(1.7-1.4)\,{\rm s}}{(\sqrt{0.75\os}-\sqrt{0.5\os})\,{\rm m}^{1/2}}$
which can be rearranged to give i y ≈ (1.89 s m−1/2)x + 0.065 s
The gradient of this line is 1.89 s m−1/2 and therefore $\left.2\pi\middle/\sqrt{g\os}\right.$ ≈ (1.89 s m−1/2) so that the estimate for the magnitude of the acceleration due to gravity is
$g = \left(\dfrac{2\pi}{1.89\,{\rm s\,m^{-1/2}}}\right)^2 = 11.05\,{\rm m\,s^{-2}}$
i
Given the intercepts on the axes
✦ Where does the line $\dfrac x5+\dfrac y3 = 1$ meet the axes?
✧ If we put x = 0 in the equation we see that the y–intercept is at (0, 3), and if we put y = 0 in the equation we see that the x–intercept is at (5, 0).
The form of the above equation makes it particularly easy to find the two intercepts; but the reverse is also true, if the intercepts are given it is straightforward to write down the equation of the line.
✦ Which of the following equations is the equation of the line with intercepts (0, 2) and (7, 0)?
(a) $\dfrac x2+\dfrac y7 = 1$ or (b) $\dfrac x7+\dfrac y2 = 1$
✧ The correct answer is (b), as we can see if we substitute first x = 0 then y = 0 into the equation.
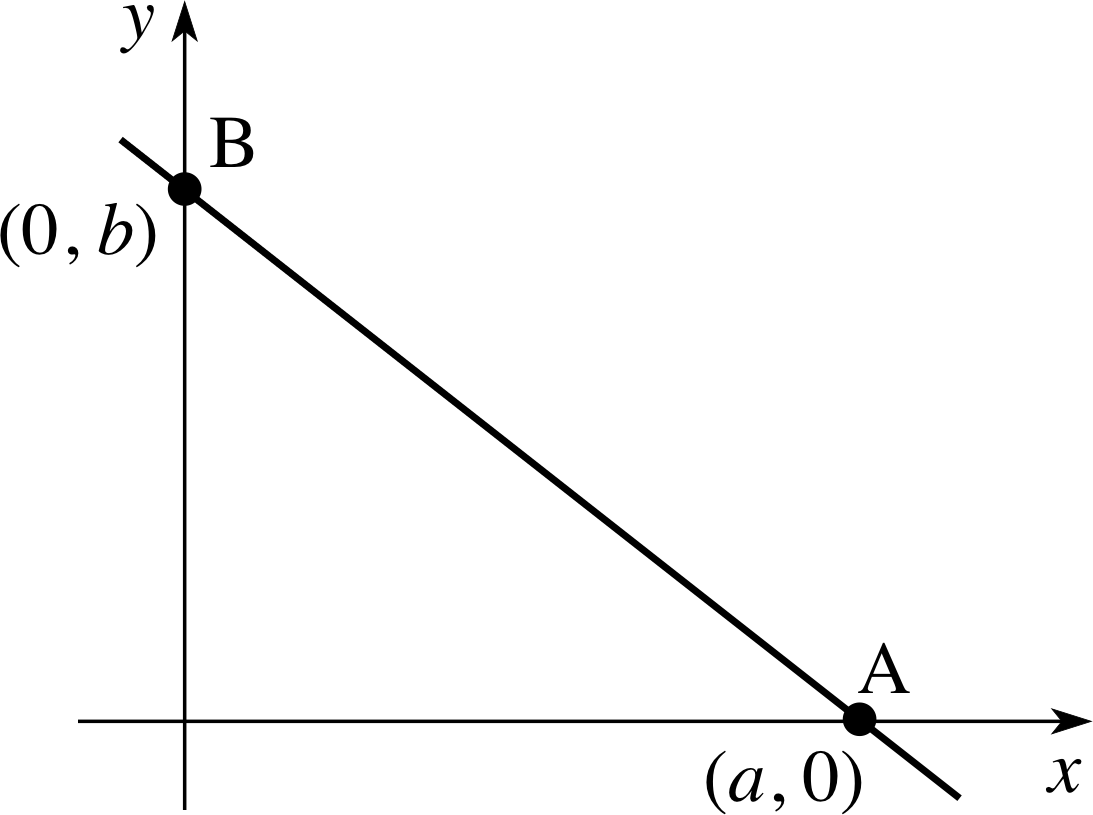
Figure 6 Graph of the straight line with given intercepts on the axes.
In Figure 6 the intercepts of the line on the x–and y–axes are A(a, 0) and y B(0, b), respectively, and the equation of the line may be written using
The intercept form of the equation of a straight line
$\dfrac xa+\dfrac yb=1$(5)
✦ What is the gradient of the line $\dfrac xa+\dfrac yb=1$?
✦ Find the equation of the line with intercepts A(1/2, 0) and B(0, −6). What is its gradient?
✧ Here a = 1/2, b = −6, so that the equation of the line is
$\dfrac{x}{1/2} + \dfrac{y}{-6} = 1$ which simplifies to $2x-\dfrac y6 = 1$.
This equation can be rearranged into the form y = 12x − 6 and we see that the gradient is 12.
We can illustrate the use of Equation 5 with the following example.
At time t, the velocity υx of an object moving in a straight line with constant acceleration ax is given by υx = u0 + axt, where u0 is its initial velocity in the x–direction. i
✦ A particle is moving in a straight line with constant acceleration, and its velocity is found to be υx1 = 10 m s−1 at time t1 = 3 s, and υx2 = 2.5 m s−1 at time t2 = 5 s. Find the acceleration of the particle, estimate the time when its velocity will be zero, and also the initial velocity of the particle.
✧ The equation υx = u0 + axt, represents the equation of a straight line (in the form of Equation 1)
$y = \underbrace{m}_{\color{purple}{\large\text{gradient}}} x + \underbrace{c}_{\color{purple}{\large{y-\text{intercept}}}}$(Eqn 1)
where the variables have been changed, so that x has been replaced by t, y has been replaced by υx , c has been replaced by u0, and m has been replaced by ax.
We are told that the points (t1, υx1) and (t2, υx2) lie on this line, so we may use Equation 4,
$\dfrac{y - y_1}{x - x_1} = \dfrac{y_2 - y_1}{x_2 - x_1}$(Eqn 4)
(with appropriate change of variables) to give
$\dfrac{v_x - v_{x1}}{t - t_1} = \dfrac{y_2 - y_1}{t_2 - t_1}$
If we rearrange this equation and substitute in the values, we obtain
υx = (21.25 m s−1) − (3.75 m s−2)t
from which we see that the acceleration is −3.75 m s−2 and the initial velocity is 21.25 m s−1. Also the velocity will be zero when the line intercepts the t–axis, i.e.
when $t = \dfrac{21.25\,{\rm m\,s^{-1}}}{3.75\,{\rm m \,s^{-2}}} \approx 5.67\,{\rm s}$
General form of the equation of a straight line
The previous forms of the equation of a straight line have a deficiency which is not immediately apparent, as the following example is intended to show.
Example 1
Find the equation of the straight line passing through the points (1, 2) and (1, 4). Draw the line.
Solution
If we attempt to use Equation 4,
$\dfrac{y-y_1}{x-x_1} = \dfrac{y_2-y_1}{x_2-x_1}$(Eqn 4)
we obtain $\dfrac{y-2}{x-1} = \dfrac{4-2}{1-1}$
but 2 divided by zero is undefined! On the other hand, we might try to find the constants m and c in the general form
y = mx + c, in which case the point (1, 2) on the line gives
2 = m + c
while the point (1, 4) on the line gives the equation
4 = m + c
Clearly it is impossible for m + c to be equal to both 2 and 4, and we conclude that the line cannot be written in the form y = mx + c.
The form of the equation of the line becomes clear if we list some points that lie on it. Each of the points (1, 0), (1, −2), (1, 2), (1, 2.3), (1, 99) lies on the line, and for each of them the x value is 1; in fact this is the property which characterizes such points and the equation of the line is x = 1, and the line is parallel to the y–axis.
Any line parallel to the y–axis has an equation x = b for some constant b.
It is often useful to have a general form for the equation of a line that includes all possible lines. Thus
The general equation of a line in two dimensions is
ax + by + c = 0(6)
Note that by putting b = 0 we obtain the equation ax + c = 0 from which we find that x = −ac which is a line parallel to the y–axis.
✦ If b ≠ 0 find the gradient and intercept of the line ax + by + c = 0.
✧ First subtract ax + c = 0 from both sides of Equation 6 so that
by = −ax − c
Then divide both sides by b so that
$y = \dfrac{-a}{b}x - \dfrac cb$
Hence the gradient is (−a/b) and the intercept is (−c/b).
Question T4
Write the equation y = −3x − 2 in each of the three forms described in this subsection, corresponding to Equations 4, 5 and 6:
$\dfrac{y-y_1}{x-x_1} = \dfrac{y_2-y_1}{x_2-x_1}$(Eqn 4)
$\dfrac xa + \dfrac yb = 1$(Eqn 5)
ax + by + c = 0(Eqn 6)
(For Equation 4 you will need to identify two points on the line; choose these to be the points with x–coordinates 1 and −1, respectively.)
Answer T4
When x = 1, y = −5, and when x = −1, y = 1. Hence the form corresponding to Equation 4 is
$\dfrac{y+5}{x-1} = \dfrac{1+5}{-1-1} = -\dfrac62 = -3$
The intercepts are (0, −2) and (−2/3, 0) so that the form corresponding to Equation 5 is
$\dfrac{x}{-2/3} + \dfrac{y}{-2} = 1$
Adding 3x + 2 to both sides of the given equation gives us 3x + y + 2 = 0, which is in the form of Equation 6.
2.5 Intersection of two lines
Parallel lines and perpendicular lines
If two lines have the same gradient then they are parallel. For example, the lines with equations y = 2x + 3 and y = 2x − 1 are parallel.
✦ Are the lines y = x + 1, y = −x + 1 parallel?
✧ The first line has gradient 1, whereas the second equation has gradient −1; the lines are therefore not parallel.
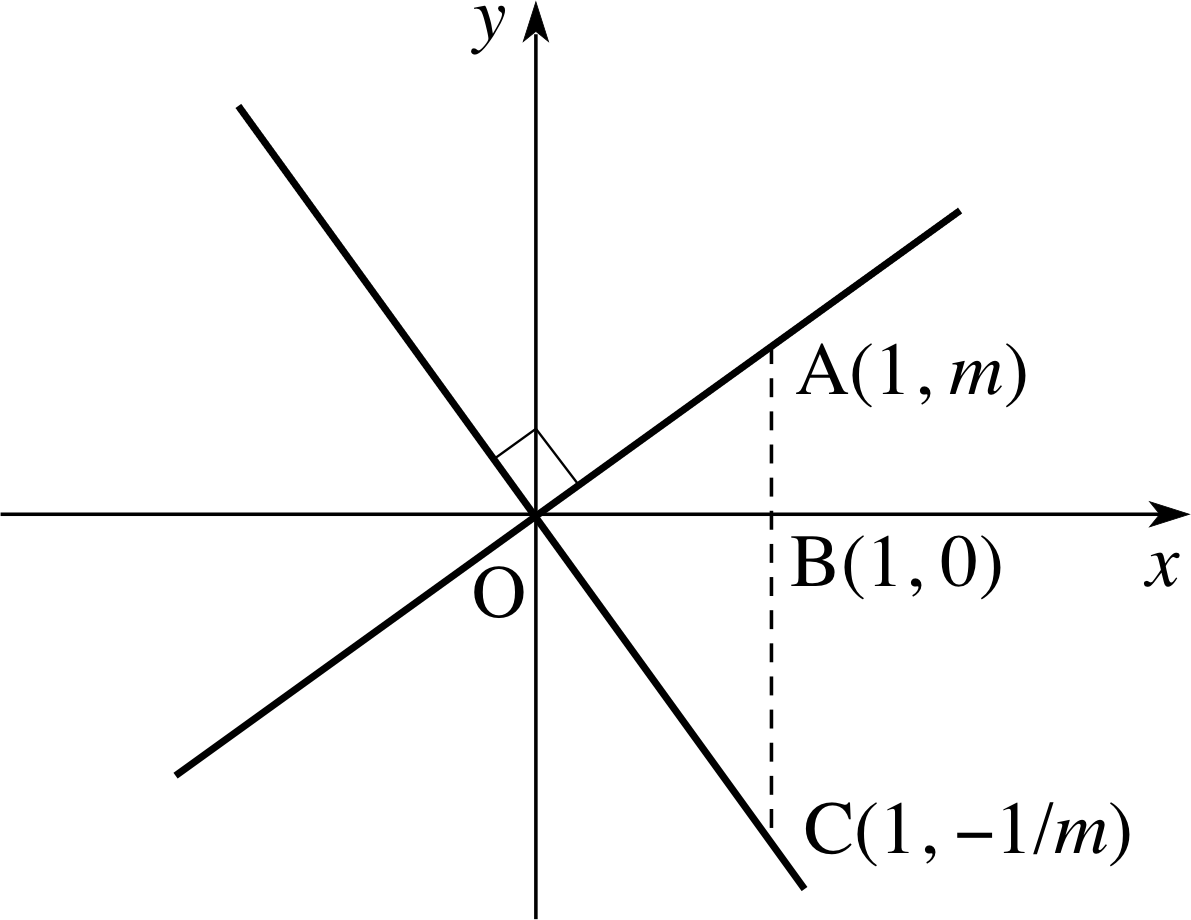
Figure 7 Two perpendicular lines through the origin.
Example 2
What is the relationship between the lines OA and OC in y Figure 7?
Solution
The line OA in Figure 7 joins the points (0, 0) and (1, m), and its equation is
y = mx
The line OC joins the points (0, 0) and (1, −1/m) and its equation is
y = −x/m
Notice that applying Pythagoras’s theorem to triangle OBA gives us
${\rm OA^2 = OB^2 + BA^2} = 1 + m^2$
and applying the same theorem to triangle OBC gives us
${\rm OC^2 = OB^2 + BC^2} = 1 + \dfrac{1}{m^2}$
It follows that
${\rm AC^2 = (AB+BC) = \left(m+\dfrac 1m\right)^2 = (1+m^2) + 1 + \left(\dfrac{1}{m^2}\right) = OA^2 + OC^2}$
and therefore (from the converse of Pythagoras’s theorem) the angle AOC is a right angle. i
The essential point to notice from Example 2 is that we have two lines through the origin, y = mx and y = −x/m, which must be perpendicular to each other for any value of m. This means, for example, that we can see instantly that the two lines y = 2x and y = −0.5x are perpendicular because the product of their gradients is −1.
We quote without proof the general result that if the equations of two lines are y = m1x + c1 and y = m2x + c2 then:
Two lines of gradient m1 and m2 are perpendicular if m2m1 = −1(7)
✦ Are the lines y = 2x + 3 and x + 2y = 4 perpendicular?
✧ The first line has gradient m1 = 2. The equation of the second line can be rearranged to give 2y = −x + 4 or y = −x/2 + 2, from which we obtain its gradient m2 = −½. Then m2m1 = −½ × 2 = −1. The lines are therefore perpendicular.
Note that the lines x = a, y = b, where a and b are constants, are perpendicular. We cannot use Equation 7 in this case (but we do not need to).
Intersection of two lines
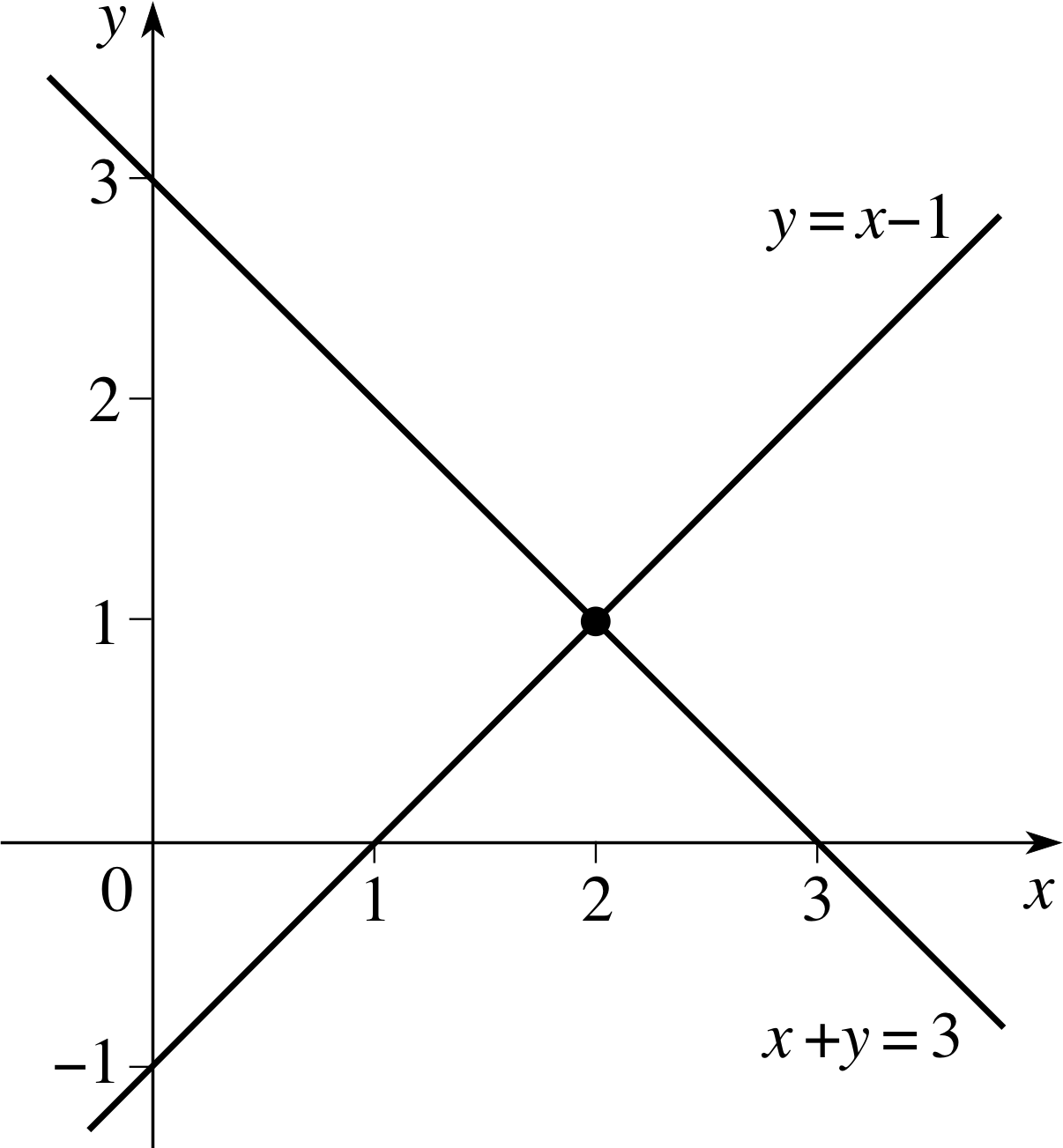
Figure 8 Intersection of two lines.
Two lines that are not parallel intersect at a point. In order to find the coordinates of the point of intersection we could certainly draw the graphs of the lines on the same set of axes, and find where they cross. The lines y = x − 1 and x + y = 3, which appear to intersect at (2, 1), are shown in Figure 8.
A graphical approach is sometimes useful, but it can be laborious and rather inaccurate, so we would prefer an algebraic method.
The equation y = x − 1 is a true statement only for points (x, y) lying on the first line, while the equation x + y = 3 is a true statement only for points (x, y) lying on the second line. If we are told that both equations are true, then we must be referring to the particular point (x, y) that lies on both lines.
A pair of equations such as
$\left. \begin{align}& &y=x-1\\ \text{and}& &x+y=3\\ \end{align}\right\}$ i
which are true for the same values of x and y are known as simultaneous equations, and they can be solved to find these values of x and y. In this instance we already suspect (from the graph) that the values x = 2 and y = 1 are the solution, and we have merely to verify that this is so by substituting these values into the equations. We do indeed find that both equations are satisfied, because 1 = 2 − 1 (the first equation) and 2 + 1 = 3 (the second equation).
Algebraic solution
There are several methods of solving a pair of simultaneous equations, but they all reduce to essentially the same idea – we use one of the equations to eliminate one of the variables, then solve the resulting equation in the remaining variable.
We will use the equations
y = x + 1(i)
2x + y = 3(ii)
to illustrate the general methods. Notice that we have numbered the equations in order to clarify the subsequent algebraic steps, and you should do likewise in your own work.
Method 1 - solving by direct substitution
We substitute for y using Equation (i) into Equation (ii) to obtain
2x + (x + 1) = 3
so that3x + 1 = 3
i.e.3x = 2
and therefore $x = \dfrac23$
Substituting this value for x into Equation (i) we find that $y = \dfrac53$.
We then check that these values also satisfy Equation (ii),
and we find $2x + y = 2 \times \dfrac23 + \dfrac53 = \dfrac43 + \dfrac53 = \dfrac93 = 3$.
Method 2 - solving by indirect substitution
We re–write the two equations as
−x + y = 1(i)
2x + y = 3(ii)
We eliminate y by subtracting Equation (i) from Equation (ii) to obtain
2x − (−x) + y − y = 3 − 1
i.e.3x = 2 as before.
Then we can use either Equation (i) or Equation (ii) to calculate y and use the other equation as a check.
Alternatively, we could begin by eliminating x, and multiply Equation (i) by 2 and add the result to Equation (ii).
−x + y = 1(i)
2x + y = 3(ii) i
−2x + 2x + 2y + y = 2 × 1 + 3
i.e.3y = 2 + 3 = 5
so that$y = \dfrac53$
Either Equation (i) or (ii) yields x = 2/3 and the other equation can be used as a check.
✦ Use the value y = 5/3 in Equation (ii) to obtain the value x = 2/3 and check the result using Equation (i).
✧ 2x + y = 3 becomes $2x + \dfrac53 = \dfrac93$, so that $2x = \dfrac43$ and hence $x = \dfrac23$.
Substituting these values for x and y into Equation (i) we obtain
$-\dfrac23+\dfrac53 = \dfrac33 = 1$
as required.
The choice of method is often a matter of taste, although sometimes the numbers involved ensure that one method is quicker than another. It can be helpful to sketch the graphs of the two lines in order to get a rough idea of where they intersect, and perhaps to give an extra check on the results.
Strange cases
There are some particular cases that may lead you to some strange results. Suppose we were asked to find the point of intersection of the lines
x − 2y = 3 and 2x − 4y = 6
and let us suppose that inspiration strikes and you guess the solution x = 5 and y = 1. You try these values in the equations, and you find that they work; so everything is fine and you have found the solution. Right?
However, the values x = −1, y = −2 also satisfy both equations.
How can this be? How can a pair of lines intersect at more than one point?
In fact, the two equations both represent the same straight line. (You can obtain the second equation by multiplying the first equation by 2). Any point on the common line has values of x and y which satisfy both equations.
Question T5
Find where the following pairs of lines intersect:
(a) y = 3x − 1, y = −2x + 2
(b) x + 2y = −1, y − 3x = 4
(c) 2x + 5y = 10, −x + 4y = 2
(d) 2x + 4y = 8, y = 2 − (1/2)x
Answer T5
(a) Substitute y = 3x − 1 into y = − 2x + 2 to obtain
$3x - 1 = -2x + 2\text{, i.e. }x = \dfrac35\text{ then }y = \dfrac95 − 1 = \dfrac45$
Intersection point is $\left(\dfrac35,\,\dfrac45\right)$
(b) The second equation can be rearranged to give y = 3x + 4. Substituting this into the first equation gives:
$x + 2(3x + 4) = -1\text{, i.e. }x = -\dfrac97\text{ then }y = -\dfrac{27}{7} + 4 = \dfrac17$
Intersection point is $\left(-\dfrac97,\,\dfrac17\right)$
(c) 2x + 5y = 10 (i)
−x + 4y = 2 (ii)
Add twice (ii) to (i)
13y = 14 so that $y = \dfrac{14}{13}$
and from Equation (i) $2x + \dfrac{70}{13}$ and hence $x = \dfrac{30}{13}$
Intersection point is $\left(\dfrac{30}{13},\,\dfrac{14}{13}\right)$
(d) The second equation is a rearrangement of the first so that any point on the line represents a solution. Substitution would yield 0 = 0 which, whilst true, is unhelpful.
Ill-conditioned equations
Example 3
Solve the (rather unpleasant) pair of simultaneous equations
x − πy = 1(i)
and2000x − 6283y = 1995(ii)
Solution
As a first step simplify Equation (i) a little by replacing π by 3.14 say, so that Equation (i) becomes
x − 3.14y = 1(iii)
now solving Equations (ii) and (iii) (and we won’t bore you with the details) you would find a solution
$x = \dfrac{187}{30}$ ≈ 6.23 and $y = \dfrac53$ ≈ 1.67, and everything appears to be fine. However, what if you were to choose a slightly better approximation for π, will this make much difference to the final result?
Suppose that you replace π by 3.141 59, then Equation (i)
becomes
x − 3.141 59y = 1(iv)
and solving Equations (ii) and (iv)(and again we won’t bother with the details) you would find
$x = -\dfrac{310559}{3600}$ ≈ −86.27 and $y = −\dfrac{250}{9}$ ≈ −27.78
This appears to be a disaster! A minor difference in the approximation for π gives startlingly different results.
Why has it happened?
Perhaps another example will make things clearer.
Example 4
Consider the equations
x + 2y = 4(i)
20x + 40.1y = 80.1(ii)
Solution
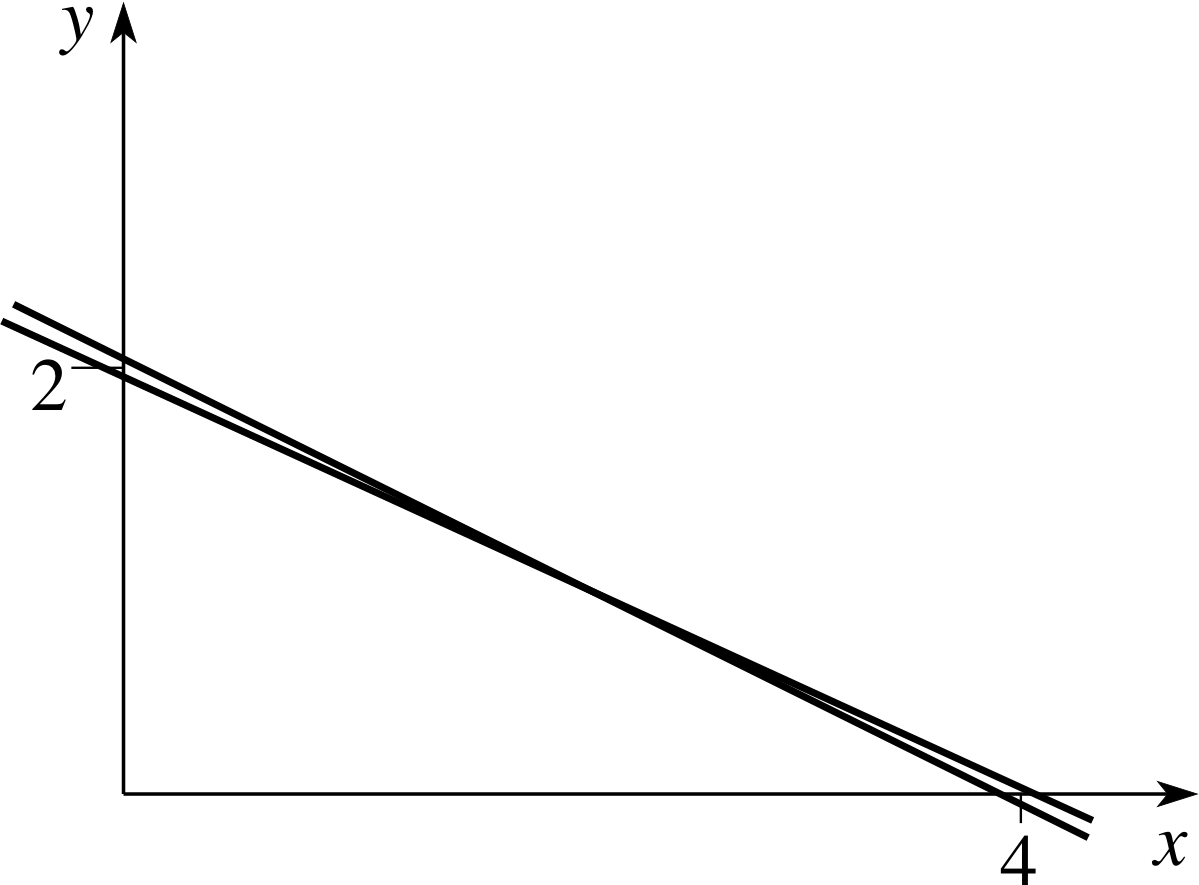
Figure 9 Graphs corresponding to ill–conditioned equations.
If we subtract 20 times Equation (i) from Equation (ii) we obtain
0.1y = 0.1
so that y = 1 and from Equation (i) we obtain x = 2. This is the (exact) unique solution. The lines intersect at the point (2, 1). However, if you look at Figure 9 you will see that the two lines are very close together and it is hard to detect precisely where the lines meet.
If the coefficient 40.1 is altered to 40, which is a change of about 1 in 400, the second equation becomes 20x + 40y = 80.1, yet when we multiply the first equation by 20 we obtain 20x + 40y = 80, which is a direct contradiction – therefore the equations have no solution (the lines are parallel). If, in addition, the value 80.1 is altered to 80 then the second equation becomes 20x + 40y = 80 which is exactly 20 times the first equation; the two lines coincide.
In such cases, where the lines are almost parallel, very slight changes in the given values of the constants can lead to massive changes in the calculated values of the solution. Such systems of equations are said to be ill–conditioned.
Question T6
Solve the following pairs of equations:
(a) 2x + y = 3 and x + 0.501y = 6
(b) 2x + y = 3 and x + 0.499y = 6
Answer T6
(a) Numbering the equations as follows
2x + y = 3 (i)
x + 0.501y = 6(ii)
2 × (ii) − (i) gives us 0.002y = 9
Hence y = 4500, and then from Equation (i) we have
$x = -\dfrac{4497}{2} = -2248.5$
(b) From the second pair of equations
2x + y = 3 (i)
x + 0.499y = 6(ii)
2 × (ii) − (i) gives us −0.002y = 9
Hence y = −4500 and then from Equation (i) we have
$x = \dfrac{4503}{2} = 2251.5$
Both pairs of equations are ill–conditioned.
2.6 Distance between two points
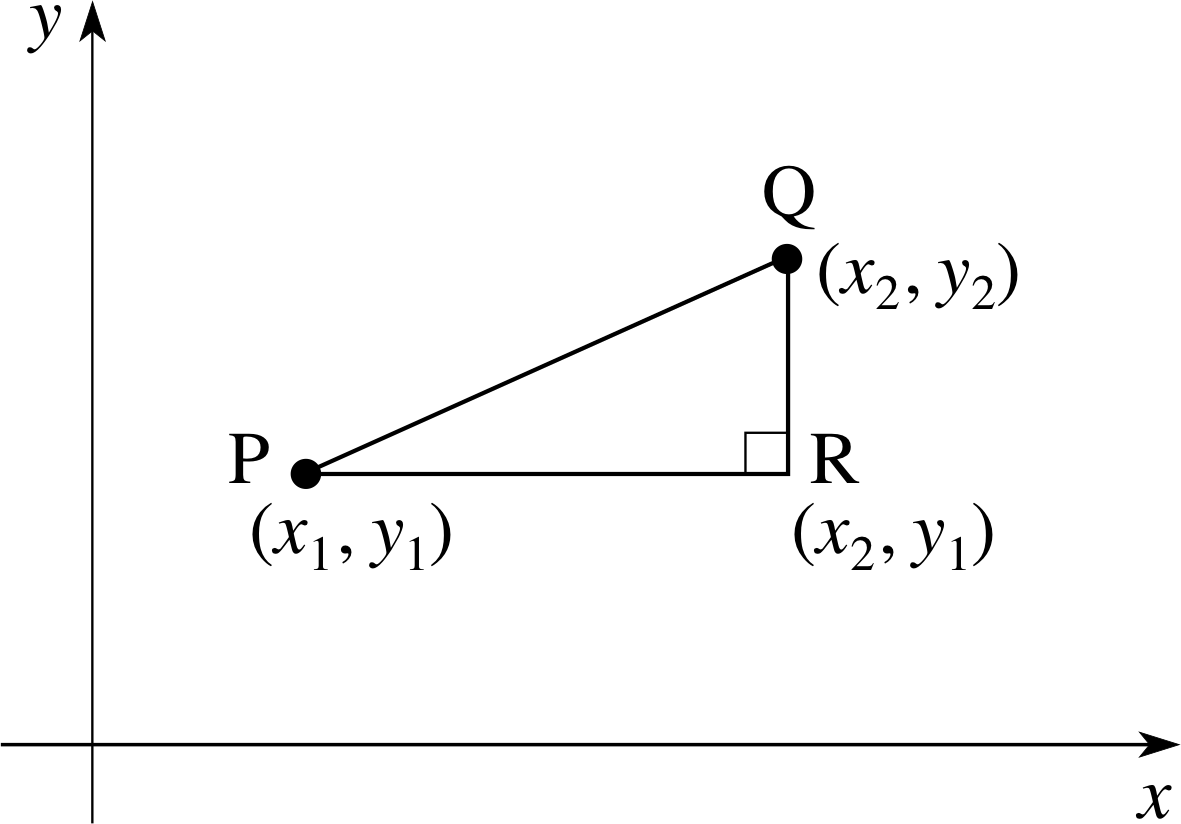
Figure 10 Distance between two points.
We have already seen in Example 2 how Pythagoras’s theorem can be used to find distances, but here we discuss the distance between two arbitrary points P and Q, as shown in Figure 10. The point R has the same y–coordinate as that of P and the same x–coordinate as that of Q.
The distance PR is the difference in the x–coordinates of P and R, i.e. (x2 − x1). The distance RQ is the difference in the y–coordinates of R and Q, i.e. (y2 − y1). Applying Pythagoras’s theorem to the triangle PQR gives the equation (PQ)2 = (PR)2 + (RQ)2, i.e. (PQ)2 = (x2 − x1)2 + (y2 − y1)2.
Hence the distance we require is given by
${\rm PQ} = \sqrt{\smash[b]{(x_2-x_1)^2 +(y_2-y_1)^2}}$(8) i
✦ Find the distance between the points P(2, −1) and Q(3, 4).
✧ Here we can put (x1, y1) = (2, −1) and (x2, y2) = (3, 4).
It follows that ${\rm PQ} = \sqrt{\smash[b]{(3-2)^2+(4-(-1))^2}} = \sqrt{1^2+5^2} = \sqrt{26\os}$
Note that it does not matter which way we label the points. If we let (x1, y1) = (3, 4) and (x2, y2) = (2, −1) the distance is still $\sqrt{26\os}$.
Question T7
Which two of the points (2, 3), (−1, 2), (3, −1) and (−2, −2) are: (a) closest to each other, (b) furthest apart?
Answer T7
Let A = (2, 3), B = (−1, 2), C = (3, −1), D = (−2, −2).
A sketch would certainly help us to decide which pairs of points to check, but if we just list all the possibilities, we have
${\rm AB} = \sqrt{\smash[b]{(2+1)^2+(3-2)^2}} = \sqrt{10\os}$
${\rm AC} = \sqrt{\smash[b]{(2-3)^2+(3+1)^2}} = \sqrt{17\os}$
${\rm AD} = \sqrt{\smash[b]{(2+2)^2+(3+2)^2}} = \sqrt{41\os}$
${\rm BC} = \sqrt{\smash[b]{(-1-3)^2+2(2+1)^2}} = \sqrt{25\os}$
${\rm BD} = \sqrt{\smash[b]{(-1+2)^2+(2+2)^2}} = \sqrt{17\os}$
${\rm CD} = \sqrt{\smash[b]{(3+2)^2 +(-1+2)^2}} = \sqrt{26\os}$
(a) Therefore A and B are closest, (b) A and D are farthest apart.
3 Circles
3.1 Equation of a circle, given its centre and radius
Our objective in this section is to determine the general equation of a circle, but first we consider a simple case, when the centre of the circle is at the origin. The point P lies on the circumference of the circle as shown in Figure 11a. Since OP is the radius of the circle its length will be the same whatever the choice of P(x, y ) on the circumference, i.e. OP = R where R is the radius of the circle. But, using Equation 8, (OP)2 = (x−0)2 +(y−0)2 = x2 +y2 and therefore the equation of the circle is
x2 + y2 = R2(9)
✦ What is the radius of the circle x2 + y2 = 4?
✧ From Equation 9 we see that R2 = 4, so that the radius R = 2. i
In the general case where the centre of the circle, C, is the point (x0, y0) in Figure 11b, it is the distance CP which is constant and equal to R. Therefore, for an arbitrary point P(x, y) on the circle, (CP)2 = R2 and so:
The standard equation of a circle with centre (x0, y0) and radius R is
(x − x0)2 + (y − y0)2 = R2(10)
✦ Write down the equations of the following circles:
(a) with centre (1, 2) and radius 5 and (b) with centre (−3, −2) and radius 3
✧ (a) (x − 1)2 + (y − 2)2 = 52 = 25
(b) (x − (−3))2 + (y − (−2))2 = 32, i.e. (x + 3)2 + (y + 2)2 = 9.
✦ Where does the line y = x + 1 meet the circle (x − 1)2 + (y − 2)2 = 4 ?
✧ If we suppose that both equations are true, then we must be referring to the point (or points) where the line meets the circle. Substituting y = x + 1 into the equation of the circle we obtain
(x − 1)2 + (x + 1 − 2)2 = 4
which simplifies to give the quadratic equation (x-1)2 = 2, so that $x = 1 \pm \sqrt{2\os}$.
Substituting these values into the equation of the line we obtain $y = 2 \pm \sqrt{2\os}$, and the points of intersection are $(1+\sqrt{2\os},\,2+\sqrt{2\os})$ and $(1-\sqrt{2\os},\,2-\sqrt{2\os})$. i
Suppose that we wish to find the points of intersection of the circles
x2 + y2 = 1(i)
and (x − 1)2 + (y +1)2 = 4(ii)
As a first step we may expand Equation (ii) to give
x2 − 2x + y2 + 2y = 2(iii)
We can now subtract (i) from (iii) to give
−2x + 2y = 1(iv)
which is the equation of a line. These equations are all true provided that we are referring to the points (x, y) where the circles meet. This means that the points where the circles meet must also lie on the line (iv). Instead of completing the calculation by finding these points we now invite you to carry out some similar calculations for yourself.
Question T8
Where do the circles (x − 1)2 + (y − 2)2 = 25 and (x + 3)2 + (y + 2)2 = 9 meet?
Answer T8
The equations of the circles are
(x − 1)2 + (y − 2)2 = 25(i)
and(x + 3)2 + (y + 2)2 = 9 (ii)
Expanding these expressions we obtain
x2 − 2x + y2 − 4y − 20 = 0(iii)
andx2 + 6x + y2 + 4y + 4 = 0 (iv)
We can eliminate both x2 and y2 by subtracting (iii) from (iv) to give
8y + 8x + 24 = 0
which simplifies to
y + x + 3 = 0(v)
which is the equation of a line. Remember that all of these equations are true provided that we are referring to
the point, or points (x, y) where the circles meet. This means that such points must also lie on the line given by Equation (v).
Substitute for y from Equation (v) into Equation (i) we obtain
(x − 1)2 + (−x − 3 − 2)2 = 25
which reduces to the quadratic equation
2x2 + 8x + 1 = 0
Hence
$x = \dfrac{-8\pm\sqrt{64-8\os}}{4} = \dfrac{-8\pm\sqrt{56\os}}{4} = -2\pm\dfrac12\sqrt{14\os}$
with corresponding values $y = -1\mp\dfrac12\sqrt{14\os}$.
The intersection points are
$\left(2+\dfrac12\sqrt{14\os},\,-1-\dfrac12\sqrt{14\os}\right)\text{ and }\left(2-\dfrac12\sqrt{14\os},\,-1+\dfrac12\sqrt{14\os}\right)$
3.2 Tangents to a circle
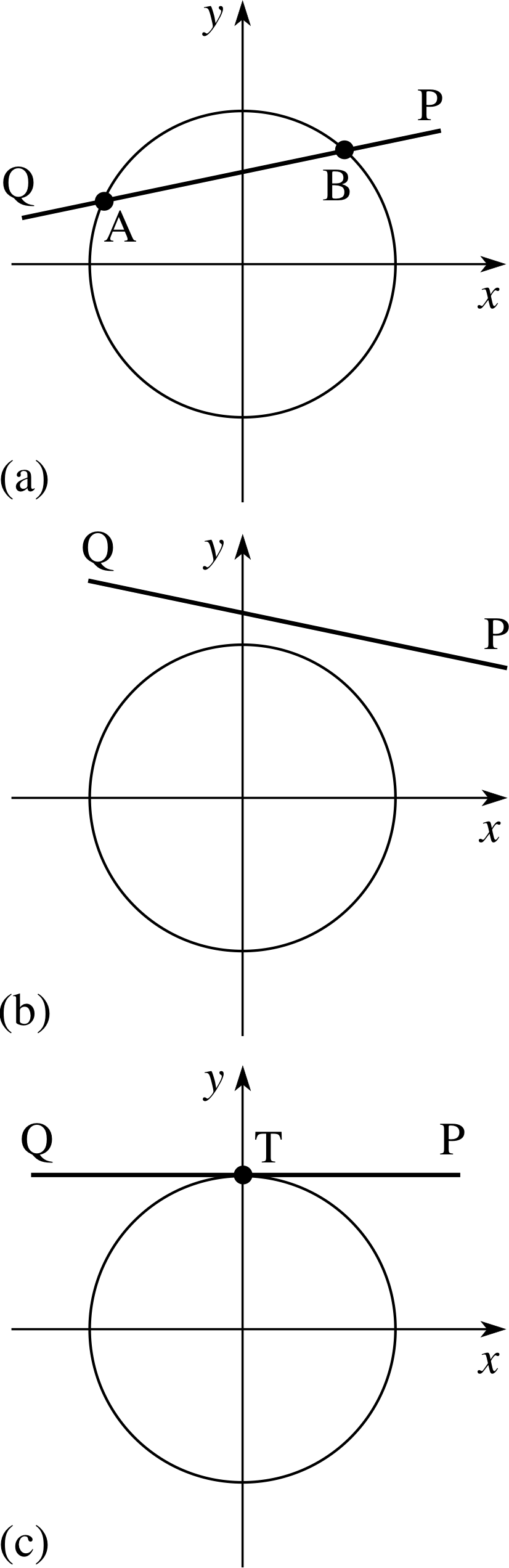
Figure 12 The intersection of a line and a circle.
In this subsection we are mainly concerned with circles whose centres are at the origin.
We consider the intersections of a straight line QP with such a circle. As depicted in Figure 12, the line could
- cut the circle at two points A and B as in diagram (a),
- not intersect the circle as in diagram (b),
- or touch the circle at one point T as in diagram (c).
In this last case the line is a tangent_to_a_curvetangent to the circle.
Let the equation of the straight line be
y = mx + c(i)
and the equation of the circle be
x2 + y2 = R2(ii)
To find where the line meets the circle we solve Equations (i) and (ii) simultaneously.
Substituting the expression for y from Equation (i) into (ii)
x2 + (mx + c)2 = R2
which can be rearranged to give a quadratic equation in x:
(1 + m2)x2 + 2mcx + (c2 − R2) = 0(iii)
Now, we know that the general quadratic equation αx2 + βx + γ = 0
- has two real roots if β2 > 4αγ
- no real roots if β < 4αγ
- one repeated real root if β2 = 4αγ
So, for the particular case of Equation (iii) there will be one root and therefore one point of contact if (2cm)2 = 4(1 + m2)(c2− R2)
i.e.4c2m2 = 4c2 + 4m2c2 − 4R2(1 + m2)
i.e.c2 = R2(1 + m2)(11)
which can be rearranged to give
$m^2 = \dfrac{c^2-R^2}{R^2}$(12)
From Equation 11,
c2 = R2(1 + m2)(Eqn 11)
we see that for any given value of m there are two values of c ; c = $R\sqrt{1 + m^2}$ and c = −R −$\sqrt{1 + m^2}$. These values of c together with the given value of m determine, via Equation (i), the two straight lines of gradient m that are tangential to a circle of radius R centred on the origin.
From Equation 12 we see that there are two values of m for any value of c provided that c < −R or c > R. These values, m = $\sqrt{c^2 - R^2}/R$ and m = − $\sqrt{c^2 - R^2}/R$, together with the given value of c, determine, via Equation (i), the two straight lines passing through y = (0, c) that are tangential to a circle of radius R centred on the origin. (Note that the condition c < −R or c > R ensures that the point (0, c) is outside the circle and thus guarantees that there are two tangents passing through that point.)
✦ Given the circle x2 +y2 =1and the line y = 2x + c find the values of c for which the line is a tangent to the circle and interpret your answer geometrically.
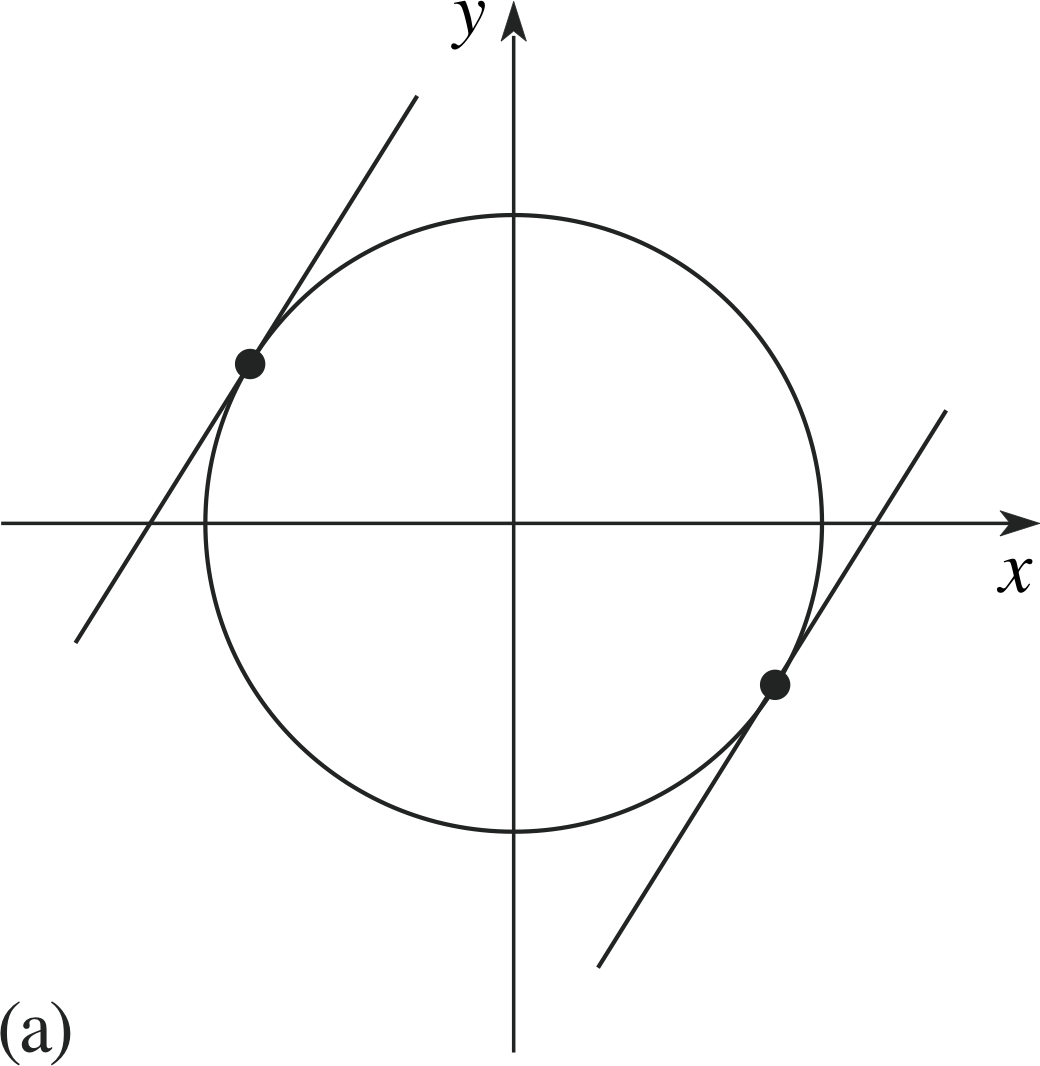
Figure 13 (a) Pairs of tangents.
✧ Figure 13a shows two tangents to the circle with the same slope.
With R = 1 and m = 2 the condition for tangency, Equation 11, is 1(1 + 4) = c2 so that c = ± $\sqrt{5\os}$. The tangent lines are therefore
y = 2x + $\sqrt{5\os}$ and y = 2x −$\sqrt{5\os}$
Figure 13a illustrates the general fact that in each direction there are two tangents to the circle.i
✦ Given the circle x2 + y2 = 25 and the point P(0,−10), find the equations of the lines through P that are tangents to the circle.
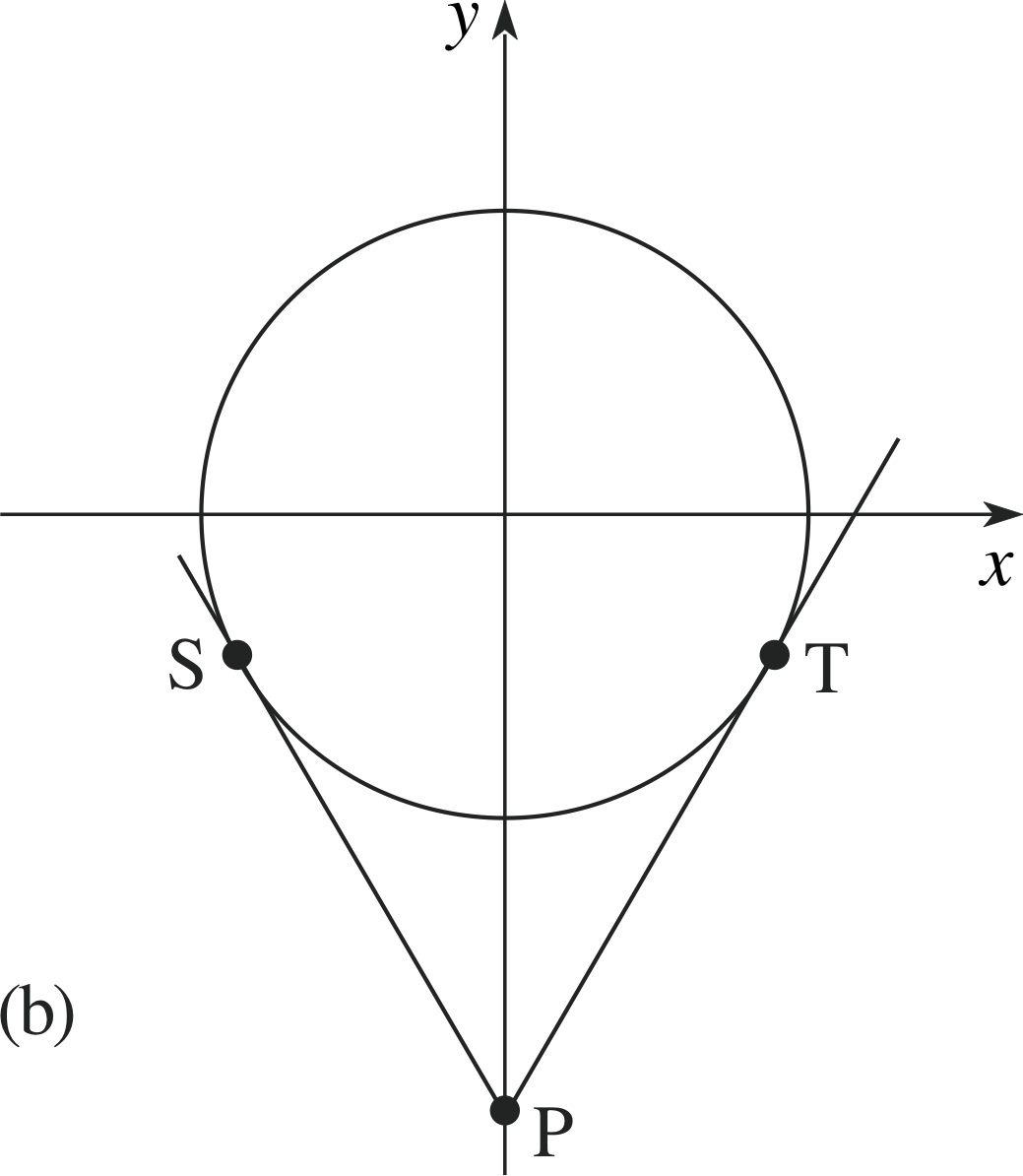
Figure 13 (b) Pairs of tangents.
✧ Refer to Figure 13b. Here R = 5, c = −10.
Hence, from Equation 11,
c2 = R2(1 + m2)(Eqn 11)
25(1 + m2) = 100
so that 1 + m2 = 4 and m = ± $\sqrt{3\os}$
Hence the equations of the tangent lines are
$y = \sqrt{3\os}x - 10$ and $y = -\sqrt{3\os}x - 10$
Equation of the tangent at a given point on a circle
We can obtain an interesting result if we consider an arbitrary point (x1,y1) and the points of intersection of the line
x1x + y1y = R2(i) i
with the circlex2 + y2 = R2(ii)
The equation of the line (i) can be rewritten as: $y=-\dfrac{x_1}{y_1}x+\dfrac{R^2}{y_1}$
(so that $m=-\dfrac{x_1}{y_1}$ and $c = \dfrac{R^2}{y_1}$ ) and this line will be a tangent to the circle if Equation 11 is satisfied,
i.e. if $ \left(\dfrac{R^2}{y_1}\right)^2 = R^2\left[1+\left(-\dfrac{x_1}{y_1}\right)^2\right]$, which reduces to x12 + y12 = R2
In other words:
the line x1x + y1y = R2(13)
is a tangent to the circle x2 + y2 = R2 provided that the point (x1, y1) lies on the circle.
✦ What is the equation of the tangent to the circle x2 + y2 = 25 at the point (4, 3) on the circle?
✧ Here (x1, y1) = (4, 3).
The equation is 4x + 3y = 25.
Question T9
(a) Show that the line y = 33.8 − 2.4x is a tangent to x2 + y2 = 169.
(b) Where is the point of contact?
(c) Write down the equation of the parallel tangent and find its point of contact.
Answer T9
(a) We can show directly that the given line is a tangent by substituting the equation of the line into that of the circle, and we obtain
x2 + (33.8 − 2.4x)2 = 169
i.e.(1 + 5.76)x2 − 2 × 2.4 × 33.8x + (33.8)2 − 169 = 0
This has equal roots if
(2 × 2.4 × 33.8)2 = 4 × 6.76 × [(33.8)2 − 169]
and you can verify that this is so by evaluating both sides.
Alternatively we can rearrange the equation of the line first into the form 2.4x + y = 33.8, then multiply both sides by 169/33.8 (to write it in the same form as Equation 13) to obtain 12x + 5y = 169. Since (12)2 + (5)2 = 169 it follows that the point (12, 5) is on the circle and hence, from Equation 13, the line is indeed a tangent.
(b) The point of contact is (12, 5).
(c) The point (−12, −5) lies at the opposite end of a diameter, and, from Equation 13, x1x + y1y = R2, the tangent at this point has equation −12x − 5y = 169, which is clearly parallel to the original line (since it has the same gradient).
So far we have only considered circles centred on the origin. However, by introducing a new system of coordinates, with axes X and Y and a different origin from that of the usual (x, y) system, we can investigate the equation of the tangent to a circle that is not centred on the origin. This is what we do in the next example.
Example 5
Given a circle of radius 5, centred on the point (−3, −4), what is the equation of a tangent to the circle through a given point on the circle?
Solution
If we make a change of coordinates to X = x − 3 and Y = y − 4 then the origin in the (x, y) coordinate system becomes the point (−3, −4) in the new (X, Y) coordinate system. If we rearrange the coordinate relations to give x = X + 3 and y = Y + 4, the circle x2 + y2 = 25, with radius 5 and centre at the origin in the (x, y) coordinate system, becomes the circle (X + 3)2 + (Y + 4)2 = 25 in the new coordinate system. In other words, its radius remains unchanged, but its centre is now at the point (−3, −4) in the (X, Y) coordinate system.
We can similarly transform the tangent xx1 + yy1 = 25, where (x1, y1) is a point on the circle in the (x, y) coordinate system, to obtain
(X + 3)x1+ (Y + 4)y1 = 25
then if we put x1 = X1 + 3 and y1 = Y1+ 4 we obtain the equation of the tangent
(X + 3)(X1+ 3) + (Y + 4)(Y1+ 4) = 25
to the circle (X + 3)2 + (Y + 4)2 = 25, where (X1, Y1) is a point on the circle in the (X, Y) coordinate system (because (X1+ 3)2 + (Y1+ 4)2 = x12 + y12 = 25).
This method of obtaining results by making a simple transformation is often a very convenient means of obtaining useful results (see Question E5).
Question T10
In this question we assume that the Earth is a perfect sphere. (You will need to use the trigonometric identities cos2 A + sin2 A = 1 and cos A cos B + sin A sin B = cos(A − B).)
(a) At time t, a point P has coordinates x = acos(ωt) and y = asin(ωt), where a > 0. Show that the point lies on a circle of radius a.
(b) Imagine now that you are looking down at the Earth from a point high above the North Pole, so that the Earth is rotating beneath you. You imagine the x– and y–axes to be two fixed directions (each perpendicular to the axis of the Earth). If P is a particular point on the Earth’s equator (so that it rotates with the Earth), how long does it take the point P to move through a complete circle, and what is the value of its angular speed ω (in radians s−1)?
(c) A satellite S is placed in a circular orbit above the Earth’s equator so that at time t its position is given by the coordinates
x = R cos(Ω t) and y = R sin(Ω t)
Take a to be the radius of the Earth. What condition involving a tangent to the Earth’s equator must be satisfied
whenever P is moving directly towards or away from the satellite? At what time t is this condition satisfed?
Answer T10
(a) Since x2 + y2 = a2 cos2 (ωt) + a2 sin2 (ωt) = a2 it follows that P lies on a circle of radius a.
(b) The point returns to its original position in one day.
1 day = (24 × 60 × 60) s = 86 400 s, and therefore (86400 s)ω = 2π radians s−1, so that ω = ( 2π/86400) radians s−1.
(c) The point P is moving directly towards, or away from the satellite, if the tangent to the circle x2 + y2 = a2 at P(a cos(ωt), a sin(ωt)) passes through the point S(R cos(Ωt), R sin(Ωt)). The equation of the tangent at P is
x1x + y1y = a2
with x1 = a cos(ωt) and y1 = a sin(ωt), so that the equation becomes
ax cos(ωt) + ay sin(ωt) = a2
which simplifies to x cos(ωt) + y sin(ωt) = a2
The point S(R cos(Ωt), R sin(Ωt)) lies on this line if
R cos(Ωt) cos(ωt) + R sin(Ωt) sin(ωt) = a
so thatcos(Ωt) cos(ωt) + sin(Ωt) sin(ωt) = a/R
i.e.cos(Ω−ω)t = a/R
Finally, the point P is moving directly towards (or away from) S if
$t = \dfrac{1}{\Omega-\omega}\arccos\left(\dfrac aR\right)$
Notice that for solutions to exist we require Ω ≠ ω, so that the satellite is moving relative to the Earth, and also a ≤ R. (A subterranean satellite is of little practical value!)
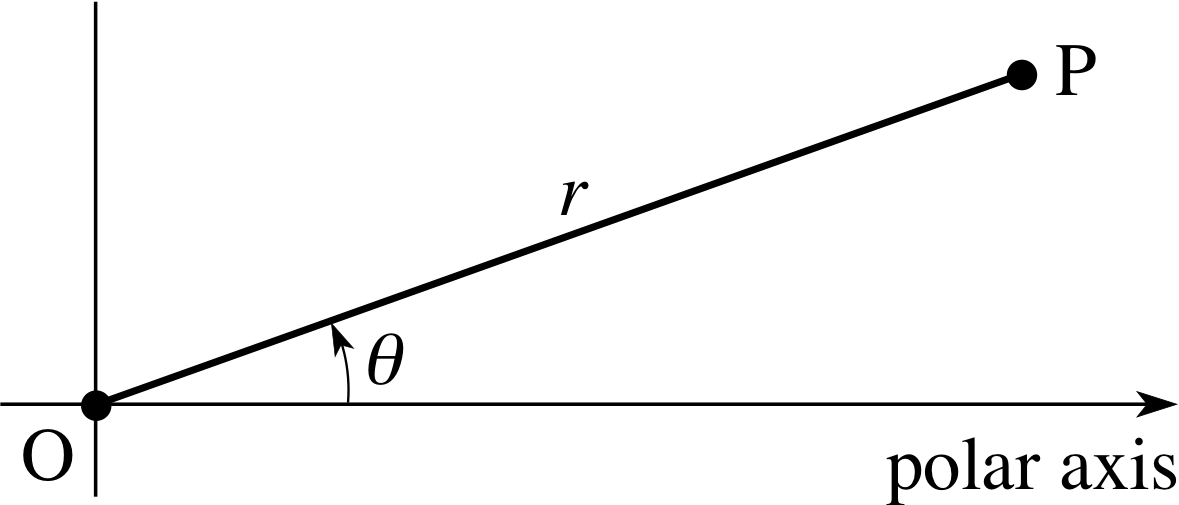
Figure 14 Polar coordinate system.
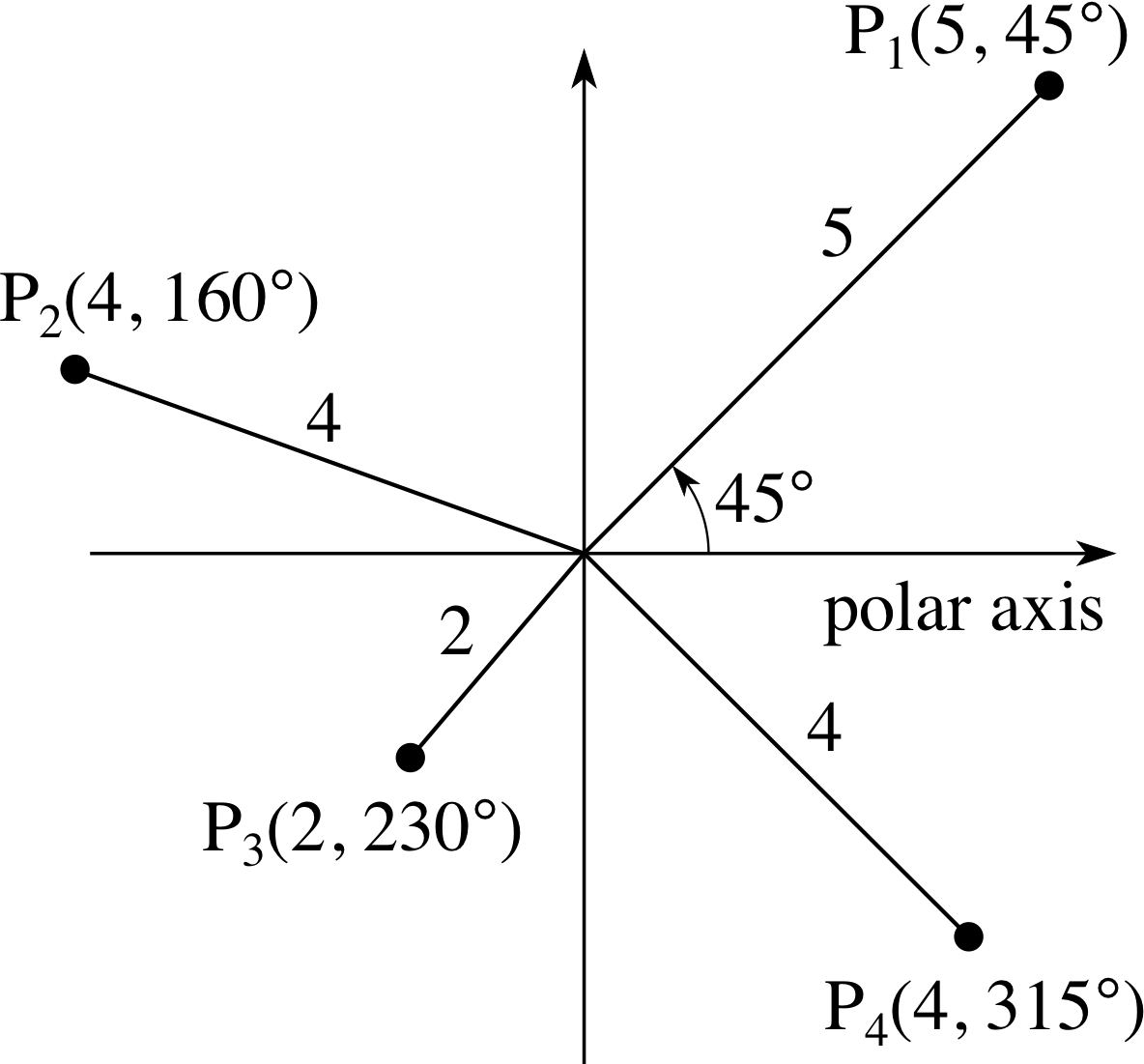
Figure 15 Some points and their polar coordinates.
3.3 Polar coordinates
Cartesian coordinates provide a valuable method of specifying the location of a point relative to a given origin, but they are not the only way in which such information can be specified. Other kinds of coordinate system exist and may be better suited to specific problems. A case in point is that of two–dimensional polar coordinates, which are particularly useful when distance from a fixed origin is of paramount importance.
The polar coordinate system is illustrated in Figure 14. The origin is represented by the point O and the point of interest by P. The line segment from O to P (sometimes called the radius vector of P) is of length r and is inclined at an angle θ, measured in the anticlockwise direction, from an arbitrarily chosen ray, called the polar axis, that emanates from O. The length r is called the radial coordinate and the θ the polar angle of P. The polar coordinates r and θ of the point P and are usually combined so that P is represented by the ordered pair (r, θ).
Figure 15 shows four points P1, P2, P3 and P4 together with their polar coordinates.
Notice that an anticlockwise rotation is taken to be positive so that, for example, the point P4 has polar coordinates (4, 315°). Since clockwise rotation is negative, and we could reach P4 by a clockwise rotation of 45° from the polar axis, its polar coordinates could be written (4, −45°).
✦ What is an alternative polar representation of P3?
✧ Since 230° = 360° − 130°, P3 can be represented as (2, −130°).
The polar coordinates of a given point are not uniquely determined, because we can add or subtract any multiple 360° to the angle. We sometimes prefer polar coordinates to be completely specified, in which case the angle θ may be restricted to lie in the range −180° < θ ≤ 180°; (although there are occasions when the range 0 ≤ θ < 360° is more convenient).
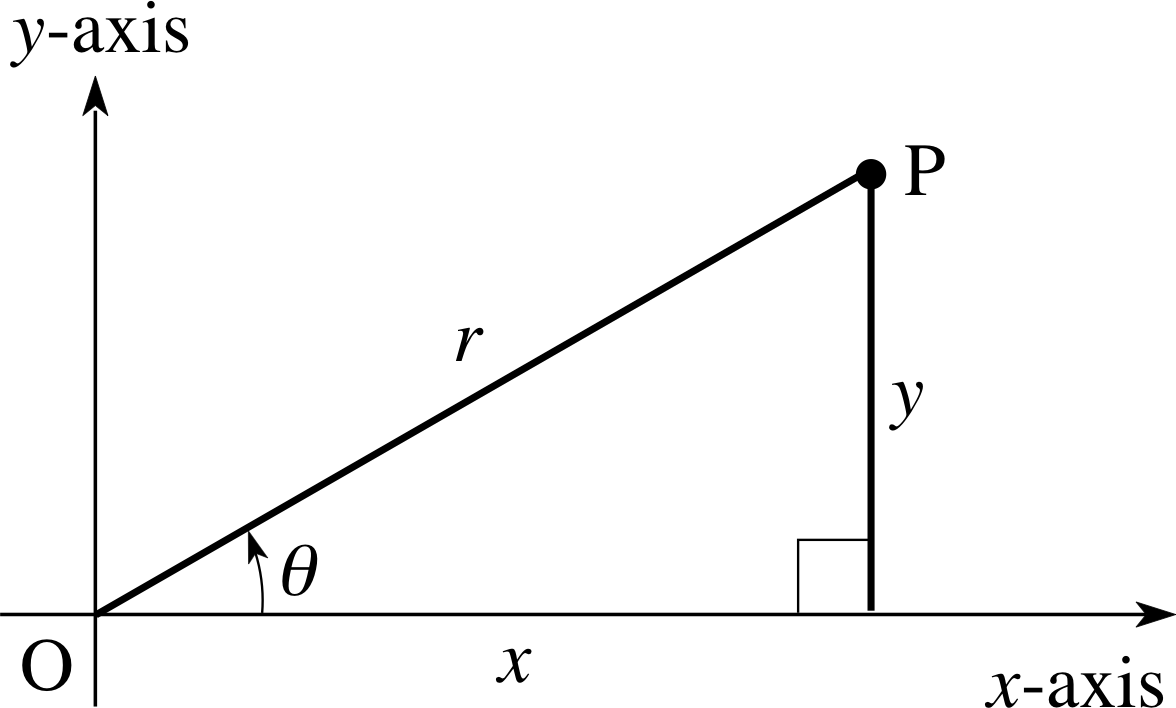
Figure 16 Polar and Cartesian coordinates.
Linking Cartesian and polar coordinates
If the origin of polar coordinates O coincides with the origin of Cartesian coordinates, and if the polar axis is chosen as the positive x–axis, we may link the Cartesian and polar coordinates as in Figure 16.
Since r is the hypotenuse of a right–angled triangle, it is clear that
x = r cos θ and y = r sin θ(14)
and these equations enable us to convert from polar to Cartesian coordinates.
✦ The polar coordinates of a point P are (5, 30°); what are its Cartesian coordinates?
✧ Since r = 5 and θ = 30°, we have
$x = 5\cos\,30° = 5 \times \dfrac{\sqrt{3\os}}{2}$ and $y = 5\sin\,30°= 5 \times \dfrac12 = 2.5$
It is also possible to deduce from Figure 16 that
r2 = x2 + y2, sin θ = y/r and cos θ = x/r(15)
and these equations enable us to convert from Cartesian to polar coordinates. Since r is a positive quantity, its determination presents no difficulty; the same is not true for θ.
Example 6
Find the polar coordinates of the point P with Cartesian coordinates (3, 4).
Solution
Since r2 = 32 + 42 = 25, we have r = 5. It remains to find an angle θ such that sin θ = 4/5 = 0.8 and
cos θ = 3/5 = 0.6. If you use a calculator to find arcsin(0.8) and arccos(0.6) you will find that both give the same result θ ≈ 53.13°.
Therefore the polar coordinates of P are approximately (5, 53.13°).
Example 7
Find the polar coordinates of the point P with Cartesian coordinates (−3, 4).
Solution
Since r2 = (−3)2 + 42 = 25, we have r = 5, as in Example 6. Also we have sin θ = 4/5 = 0.8 and cos θ = 3/5 = −0.6, and now when you use your calculator to find the angle you will find arcsin(0.8) ≈ 53.13° as before, but arccos(−0.6) ≈ 126.87°. This illustrates the limitations of your calculator, rather than a real problem in the mathematics.
The correct answer is θ ≈ 126.87° as you can very easily verify. If you use your calculator to evaluate sin(126.87°) and cos(126.87°) you will soon see that sin(126.87°) ≈ 0.8 and cos(126.87°) ≈ −0.6.
So the polar coordinates are (5, 126.87°).
You may have noticed that the two equations
sin θ = y/r and cos θ = x/r
can be combined to give tan θ = y/x, but specifying the tangent of an angle does not uniquely determine the angle, so this does not resolve the difficulty.
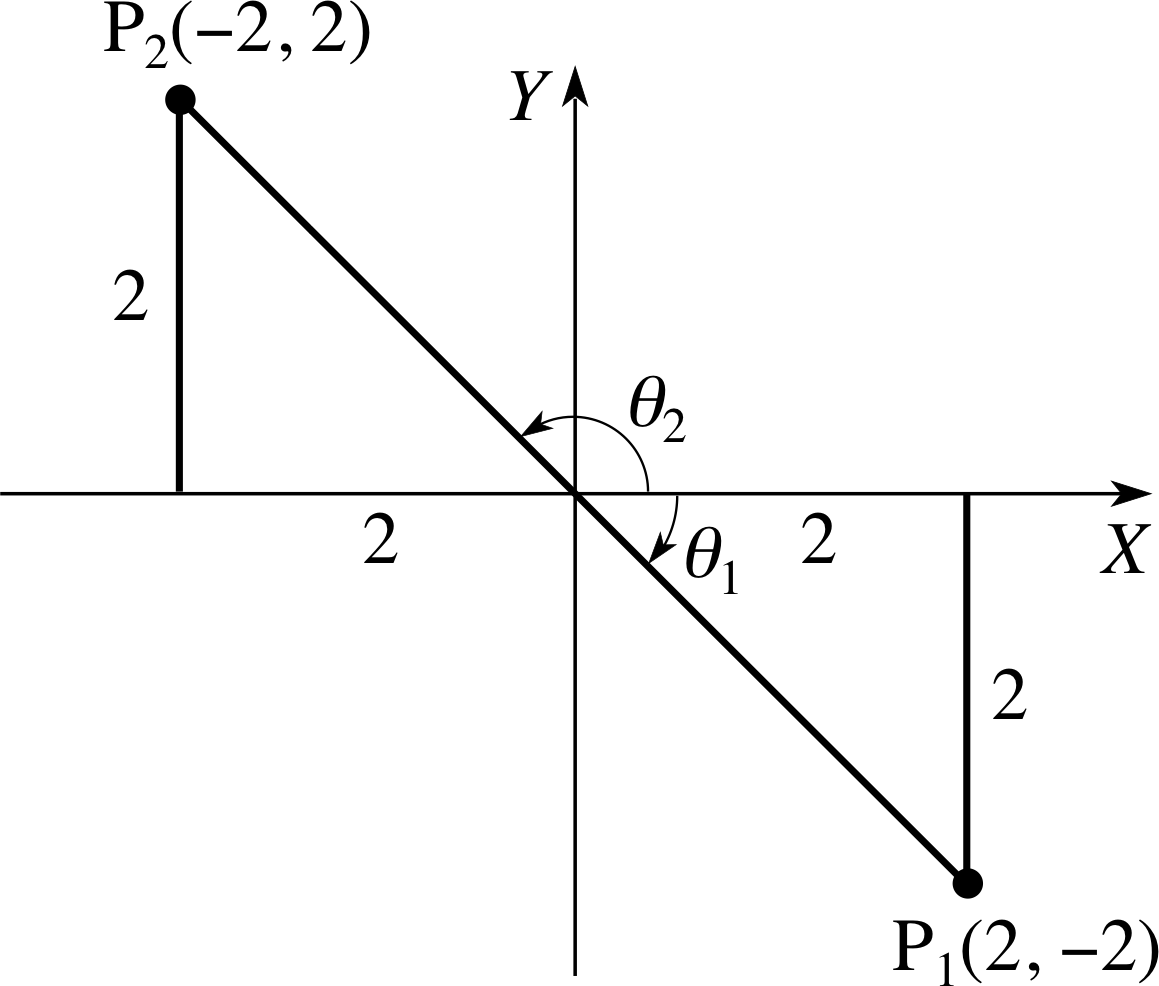
Figure 17 Points whose polar angles differ by 180°.
Example 8
Determine the polar coordinates of the points P1 and P2 with Cartesian coordinates (2, −2) and (−2, 2), respectively.
Solution
In each case r2 = 22 + 22 = 8 so that r = $2\sqrt{2\os}$.
In each case tan θ = −1, and my calculator gives arctan(−1) = −45°, but P1 and P2 are clearly different points. The answer to our problems is to construct a sketch and plot the points, see Figure 17.
If we plot the point (2, −2) we can see at once that the angle θ1 is 45°, and, since it is measured clockwise from OX the polar coordinates of P1 are ($2\sqrt{2\os}$, −45°), or equivalently ($2\sqrt{2\os}$, 315°). The angle θ2 is 180° − 45° = 135° and the polar coordinates of P2 are ($2\sqrt{2\os}$, 135°).
The message is clear:
When determining the polar angle θ it is wise to sketch a diagram to show the position of the point.
4 Three–dimensional geometry
4.1 Points in three dimensions
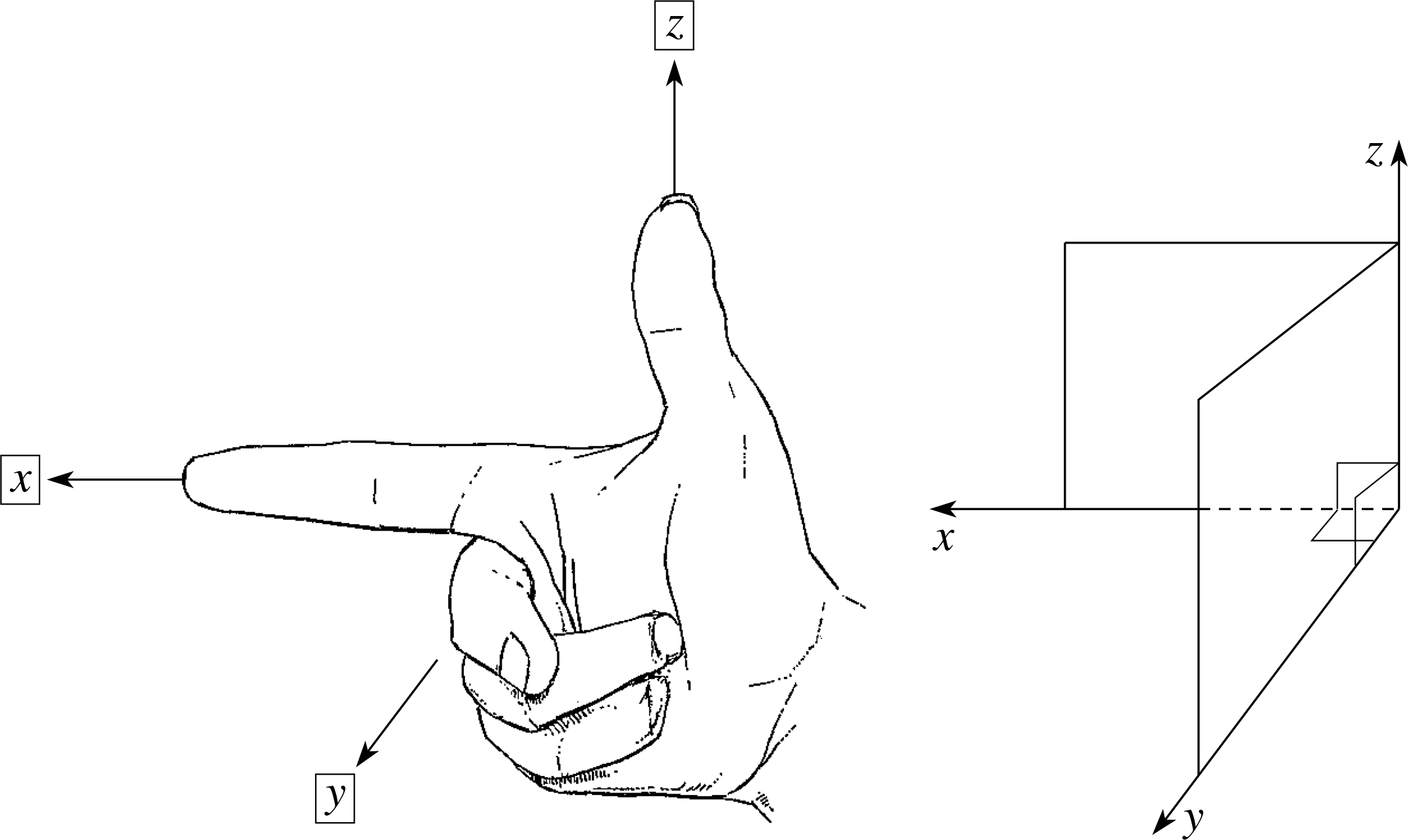
Figure 19 Picture of a hand showing the directions of the axes in a right–handed Cartesian coordinate system.
We need two pieces of information to determine the position of a point in a plane, but in three dimensions we need to provide three independent pieces of information.
Figure 18 shows a Cartesian coordinate system in three dimensions. The point N is ‘vertically’ below the point P so that the line NP is parallel to the z–axis.
A point O is chosen as the origin of coordinates and three mutually perpendicular rays x, y and z are drawn as shown. The position of P is specified by three coordinates: x, y and z as indicated; and we refer to the point as P(x, y, z). Having decided on the x– and y–axes, there are two possible directions, opposite to one another, in which the z–axis can be directed, so that it is normal (i.e. perpendicular) to both the x– and y–axes.
To remove any ambiguity about the choice of direction of the z–axis, a right–handed Cartesian coordinate system is almost invariably used. There are various ways of describing this system, but one simple method only is included here.
If the thumb and first two fingers of the right hand are arranged so that they are approximately mutually perpendicular as in Figure 19, then, if the first and second finger point along the x– and y–axes, respectively, the thumb points along the z–axis in a right–handed system.
✦ Which of the following is a right–handed coordinate system:
(a) x points west, y points north and z points vertically upward,
(b) x is vertically downward, y points south and z points west?
✧ Case (b) is right-handed, case (a) is not.
Distance between two points
The distance OP in Figure 18 can be found by applying Pythagoras’s theorem twice. In the horizontal plane which contains the x– and y–axes,
(ON)2 = (OL)2 + (LN)2
In the vertical plane which contains the lines ON, NP and OP,
(OP)2 = (ON)2 + (NP)2 = (OL)2 + (LN)2 + (NP)2
Hence(OP)2 = x2 + y2 + z2
Now we consider the distance between two general points.
Let the two points be P1(x1, y1, z1) and P2(x2, y2, z2). We can ‘move’ the point P1 to the origin by subtracting x1 from its first coordinate, y1 from its second coordinate and z1 from this third coordinate (this has the same effect as moving the origin to the point P1). The same transformation will move P2 to a point whose coordinates are (x2 − x1, y2 − y1, z2 − z1). If we call this point P we can apply the result just obtained to determine the distance between P1 and P2. Thus the distance d between the points (x1, y1, z1) and (x2, y2, z2) is given by
d2 = (x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2(16)
✦ What is the distance between the points (1, 2, −3) and (−2, 0, 4)?
✧ Let x1 = 1, y1 = 2, z1 = −3, x2 = −2, y2 = 0, z2 = 4.
The distance d is given by
d2 = (−2 − 1)2 + (0 − 2)2 + (4 − (−3))2 = (−3)2 + (−2)2 + (7)2 = 9 + 4 + 49 = 62.
Hence d = $\sqrt{62\os}$.
It is worth noting that the formula for the distance between two points in two dimensions (Equation 8)
${\rm PQ} = \sqrt{\smash[b]{(x_2 - x_1)^2 + (y_2 - y_1)^2}}$(Eqn 8)
is the special case of the formula for three dimensions, i.e. Equation 16, with z1 and z2 both put equal to zero.
Question T11
Which of the following points are (a) closest together, (b) furthest apart: (1, 2, 3), (−1, −2, −1), (2, 2, −2), (3, 0, 1)?
Answer T11
Let A = (1, 2, 3), B = (−1, −2, −1), C = (2, 2, −2), D = (3, 0, 1)
${\rm AB} = \sqrt{2^2+4^2+4^2} = \sqrt{36\os}$
${\rm AC} = \sqrt{\smash[b]{(-1)^2+0^2+5^2}} = \sqrt{26\os}$
${\rm AD} = \sqrt{\smash[b]{(-2)^2+2^2+2^2}} = \sqrt{12\os}$
${\rm BC} = \sqrt{\smash[b]{(-3)^2+(-4)^2+1^2}} = \sqrt{26\os}$
${\rm BD} = \sqrt{\smash[b]{(-4)^2+(-2)^2+(-2)^2}} = \sqrt{24\os}$
${\rm CD} = \sqrt{\smash[b]{(-1)^2+2^2+(-3)^2}} = \sqrt{14\os}$
(a) A and D are closest, and (b) A and B are farthest apart.
4.2 Planes in three dimensions
A plane is a flat surface which has the property that a straight line joining any two points in the plane lies entirely in the plane itself.
The general equation of a plane in three dimensions is often written as
ax + by + cz = d(17)
where a, b, c and d are constants. Note that if we choose a = 1 with b = c = d = 0 the equation becomes x = 0 which is the (y, z) plane.
✦ What values of a, b, c, d correspond to (a) the (x, y) plane, (b) the (z, x) plane?
✧ (a) a = b = d = 0 gives cz = 0 and if c ≠0 then z = 0 which is the equation of the (x, y) plane.
(b) a = c = d = 0, gives by = 0 and if b ≠0 then y = 0 which is the equation of the (z, x) plane.
Other planes can be described by choosing suitable combinations of the constants a, b, c and d. The plane z = 2 is parallel to the plane z = 0 (the (x, y) plane) and cuts the z–axis at z = 2, i.e. the point (0, 0, 2). The equation z = 2 corresponds to Equation 17 with a = 0, b = 0, c = 1 and d = 2.
✦ The three points (1, 3, 5), (1, −2, 7), (1, −1, 0) lie in a plane. What is the equation of the plane?
✧ The x-coordinate of all three points is 1, and therefore the equation for the plane is x = 1.
Note that if d = 0 in Equation 17 then the plane will pass through the origin, since x = y = z = 0 will satisfy the equation of the plane.
Intersection of two planes
If two planes are not parallel then they meet in a line. Imagine two consecutive pages of a book. Hold the pages taut and you see that they meet in the line of the binding connecting them. For example the (x, y) plane meets the (y, z) plane on the y–axis, this means that the y–axis corresponds to the points where both x and z are zero; in other words, we can see instantly that a point such as (0, 5, 0) must lie on the y–axis.
✦ Which axis corresponds to the intersection of the two planes x = 0 and y = 0?
✧ The z–axis.
✦ Where does the plane x + y + 2z = 6 meet the x–, y– and z–axes?
✧ The plane meets the x–axis when y = z = 0, so that x = 6, i.e. at the point (6, 0, 0).
Similarly the plane meets the y–axis at (0, 6, 0), and the z–axis at (0, 0, 3).
If we keep the values of a, b and c fixed in Equation 17,
ax + by + cz = d(Eqn 17)
but double the value of d, we obtain a plane that is parallel to the original plane (but twice as far from the origin). Compare the results of the following exercise with those of the previous exercise.
✦ Where does the plane x + y + 2z = 12 meet the x–, y- and z–axes?
✧ The plane meets the x–axis when y = z = 0, so that x = 12, i.e. at the point (12, 0, 0). Similarly the plane meets the y–axis at (0, 12, 0), and the z–axis at (0, 0, 6).
Question T12
Find the equation of a plane that is parallel to the plane 3x − 4y + z = 2 and passes through the point (1, 2, 3). i
Answer T12
The required equation must be of the form 3x − 4y + z = d for some suitably chosen value of d. The point (1, 2, 3) lies on the plane, so that the values x = 1, y = 2 and z = 3 must satisfy the equation.
It follows that (3 × 1) − (4 × 2) + 3 = d and therefore d = −2, so the required equation is
3x − 4y + z = −2
4.3 Lines in three dimensions
In three dimensions, straight lines are often specified by the intersection of two planes. Of course we try to choose the planes so that the specification is as neat as possible; for example, we could specify a line as the intersection of the planes
3x − 2y = 5
and5y − 3z = −11
but this specification is not as neat as it might be. The first of these equations can be rewritten in the form $\dfrac{x-1}{2} = \dfrac{y+1}{3}$ while the second can be rewritten in the form $\dfrac{y + 1}{3} = \dfrac{z-2}{5}$, so that the two equations can be combined into the particularly neat form
$\dfrac{x-1}{2} = \dfrac{y+1}{3} = \dfrac{z-2}{5}$(18) i
In this form we can see instantly that the point (1, −1, 2) must lie on the line. The values 2, 3 and 5 are also significant, since they can be used to determine the direction of the line (but it would take us beyond the scope of this module to explain how this is done).
If we put each of the fractions in Equations 18 equal to s, then they can be written in the equivalent form
$\left.\begin{align} x&=1+2s\\y&=-1+3s\\z&=2+5s\\ \end{align} \right\}$(19)
The variable s is then a parameter that moves the point (x, y, z) up and down the line as we change its value. It is often this form of the equations of a line which is most useful, as the following exercise illustrates.
✦ Where does the line $\dfrac{x-1}{2} = \dfrac{y+1}{3} = \dfrac{z-2}{5}$ meet the plane x + 2y + 3z = 1?
✧ First we write the equations of the line in the form of Equation 19,
$\left.\begin{align}x & =1+2s\\y & =-1+3s\\z & = 2+5s\\ \end{align}\right\}$(Eqn 19)
then substitute for x, y and z into the equation of the plane. This gives the following equation for s
(1 + 2s) + 2(−1 + 3s) + 3(2 + 5s) = 1
which simplifies to give s = −4/23 ≈ −0.17.
We can now find the values of x, y and z by substituting this value of s into the equations of the line, and we find the point of intersection (0.66, −1.51, 1.15)
In three dimensions only lines that lie in a plane will meet in a point. Indeed, in three dimensions, it is more likely that a pair of lines chosen at random will not meet, in which case they are said to be skew lines.
In general, the equations of a line in three dimensions
$\dfrac{x-a}{l} = \dfrac{y-b}{m} = \dfrac{z-c}{n}$(20)
specify a line through the point (a, b, c) and the constants l, m, n are known as the direction ratios (or direction cosines) of the line.
✦ Find the equations of a line through the points (1, 2, 3) and (6, 5, 4).
✧ We can see at once that the equations can be written in the form of Equation 20.
$\dfrac{x-1}{l} = \dfrac{y-2}{m} = \dfrac{z-3}{n}$
But the point (6, 5, 4) lies on the line, and therefore
$\dfrac{6-1}{l} = \dfrac{5-2}{m} = \dfrac{4-3}{n}$
i.e.$\dfrac 5l = \dfrac 3m = \dfrac 1n$
and we can see that l = 5, m = 3 and n = 1 provide a solution to these equations.
The required equations are therefore
$\dfrac{x-1}{5} = \dfrac{y-2}{3} = \dfrac{z-3}{1}$
Question T13
Given the equations of a line in the form
x = 1 + 2s, y = −2 + s, z = 2 − 3s
(where s can take any value), show that the point P(1, −2, 2) lies on the line. Find the points on the line that are at a distance $\sqrt{14\os}$ from P. Make s the subject of each equation i and hence find the direction ratios for the line.
Answer T13
The value s = 0 gives x = 1, y = −2, z = 2 so the point P(1, −2, 2) lies on the line. Let the required point be Q(1 + 2s, − 2 + s, 2 − 3s), and notice that this point must lie on the line. Then, from Equation 16, we have PQ2 = (2s)2 + s2 + (3s)2 = 14, so that s2 = 1 and = ±1. It follows that the possible choices for Q are (3, −1, −1) and (−1, −3, 5).
$s = \dfrac{x-1}{2} = \dfrac{y+2}{1} = \dfrac{z-2}{-3}$
The direction ratios are 2, 1, and −3.
5 Closing items
5.1 Module summary
- 1
-
In two dimensions the Subsection 2.1Cartesian system of coordinates consists of two perpendicular lines, called axes, which meet at the origin of coordinates; one of these lines, usually drawn horizontally, is designated the x–axis, the other, which is usually drawn vertically, is the y–axis. The x–coordinate of a point is the perpendicular distance of that point from the y–axis, with a negative sign attached if the point lies to the left of the y–axis. The y–coordinate of the point is its perpendicular distance from the x–axis, with a negative sign attached if the point lies below the x–axis.
- 2
-
The equation of a straight line can appear in a variety of forms; the one chosen depends on the information available about the line and the information likely to be required about the line.
- 3
-
If the line has a known gradient m and a known intercept (on the y–axis) c then the equation relating the x– and y–coordinates of a point on it is
y = mx + c(Eqn 1)
- 4
-
If the line has a known gradient m and passes through the point (x1, y1) then the equation of the line is
y − y1 = m (x − x1)(Eqn 3)
- 5
-
If the line meets the x–axis at x = a and the y–axis at y = b then the equation of the line is
ax + by = 1(Eqn 5)
- 6
-
The so–called general form of the equation of a line is
ax + by + c = 0(Eqn 6)
- 7
-
If two lines are parallel then their gradients are equal, and if two lines are perpendicular then the product of
their gradients is −1.
- 8
-
If two lines intersect then the coordinates of the point of intersection can be found by solving
simultaneously the equations of the lines.
- 9
-
The distance between the points P(x1, y1) and Q(x2, y2) is given by
${\rm PQ} = \sqrt{\smash[b]{(x_2 - x_1)^2 + (y_2 - y_1)^2}}$(Eqn 8)
- 10
-
The equation of a Section 3circle centred at the origin and of radius R is
x2 + y2 = R2(Eqn 9)
- 11
-
The equation of a circle centred at the point (x0, y0) and of radius R is
(x − x0)2 + (y − y0)2 = R2(Eqn 10)
- 12
-
The equation of the Subsection 3.2tangent to the circle x2 + y2 = R2 at a point (x1, y1) on the circle is given by
x1x + y1y = R2(Eqn 13)
- 13
-
In the Subsection 3.3polar coordinate system a point is specified by its distance r from the origin and the polar angle θ which it makes with a given line through the origin. The link between the two systems is provided by the pair of equations
x = r cos θ and y = r sin θ(Eqn 14)
andr2 = x2 + y2, sin θ = y/r, cos θ = x/r(Eqn 15)
where we must take care to identify the correct value of θ. (This can often be done by plotting the point on a diagram, and then using the fact that tan θ = y/x.)
- 14
-
The distance d between the points (x1, y1, z1) and (x2, y2, z2) in three dimensions is given by
d2 = (x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2(Eqn 16)
- 15
-
The general equation of a plane in three dimensions is
ax + by + cz = d(Eqn 17)
If two planes intersect, they do so in a line.
- 16
-
The general equations of a line in three dimensions are
$\dfrac{x-a}{l} = \dfrac{y-b}{m} = \dfrac{z-c}{n}$(Eqn 20)
where (a, b, c) is a point on the line and l, m, n are constants, known as direction ratios lmn (or direction cosines) of the line.
5.2 Achievements
Having complete this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Set up a Cartesian coordinate system and plot points in it.
- A3
-
Recognize the different forms of equation of a straight line and produce the appropriate equation from the information given about the line, then derive the required information from it.
- A4
-
Convert one form of the equation of a line into another.
- A5
-
Write down the equation of a circle, given its centre and radius, and deduce the centre and radius of a circle from its equation.
- A6
-
Produce the equation of tangents to a circle, both from a given point outside the circle and at a given point of contact on the circle.
- A7
-
Set up the polar coordinate system, plot points in it and convert from Cartesian coordinates to polar coordinates and vice versa.
- A8
-
Calculate the distance between two points in three dimensions.
- A9
-
Recognize the equation of a plane, and use it to indentify points that lie in the plane.
- A10
-
Recognize the equations of a line in three dimensions and use them to identify points that lie on the line and the point at which a line intersects a given plane.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
5.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
Plot the following points on a coordinate system: A(−1, 4), B(3, −1), C(−4, −1), D(0, 2), E(0, −3).
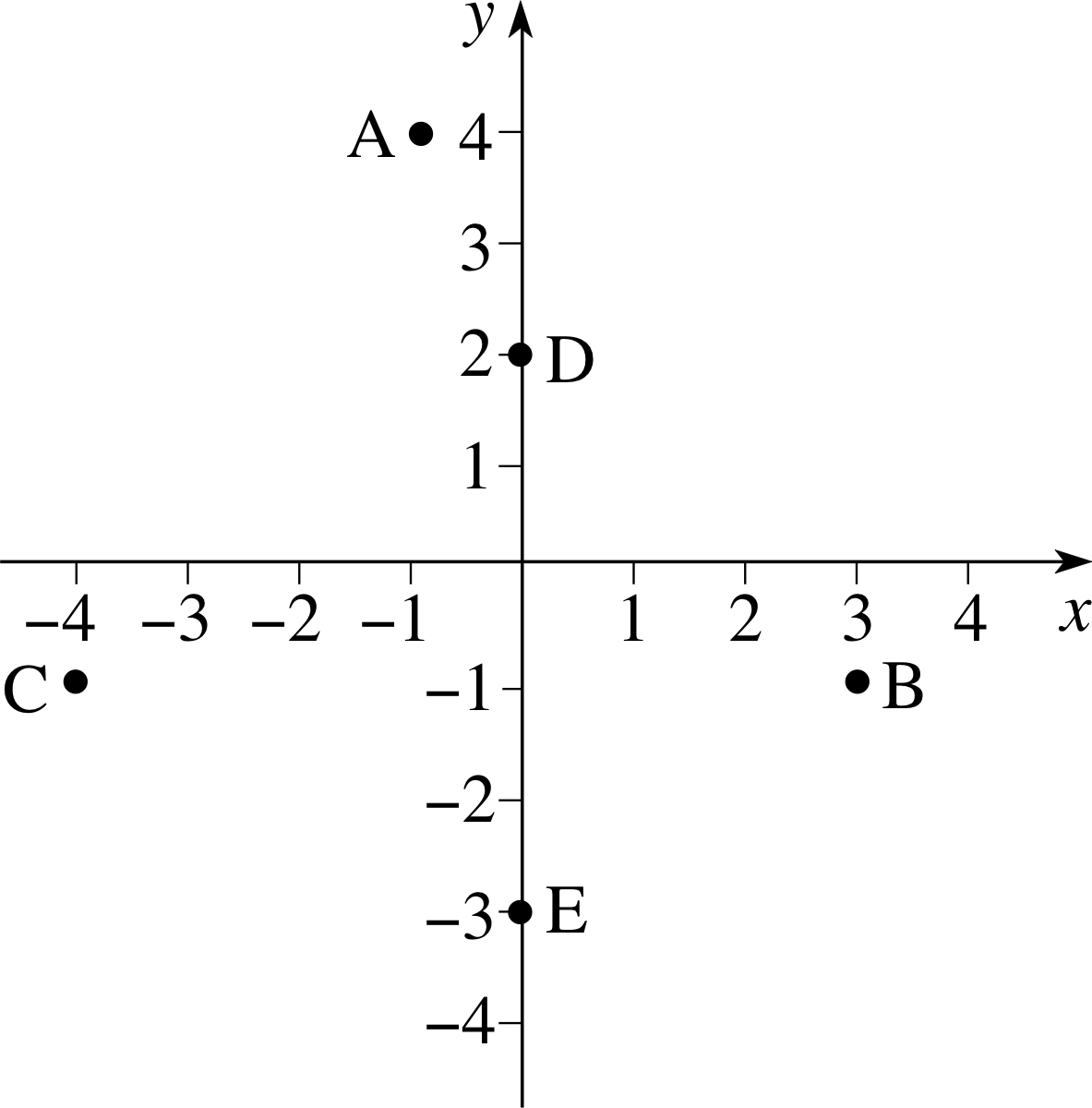
Figure 20 See Answer E1.
Answer E1
The points are plotted in Figure 20.
(Reread Subsection 2.1 if you had difficulty with this question.)
Question E2 (A3)
Find the equations of the following lines:
(a) with gradient −5 and y–intercept −2
(b) with gradient −2, passing through the point (−1, 4)
(c) passing through the points (2, − 3) and (−1, −1)
(d) with intercepts at −2 on both axes.
Answer E2
(a) y = −5x − 2
(b) y − 4 = −2(x + 1), which can be simplified to y = −2x + 2
(c) $\dfrac{y+3}{-1+3} = \dfrac{x-2}{-1-2}$, i.e. $\dfrac{y+3}{2} = \dfrac{x-2}{-3}$
which can be simplified to −3y − 9 = 2x − 4
i.e. −3y = 2x + 5 or $y = -\dfrac23x-\dfrac53$
(d) $\dfrac{x}{-2} + \dfrac{y}{-2}=1$, which can be simplified to y = −x − 2
(Reread Section 2 if you had difficulty with this question.)
Question E3 (A4)
Rewrite each of the equations in Question E2 in the general form ax + by = c.
Answer E3
(a) 5x + y = −2
(b) 2x + y = 2
(c) 2x + 3y = −5
(d) x + y = −2
(Reread Section 2 if you had difficulty with this question.)
Question E4 (A3)
Find the gradient and y–intercept for the line of Question E2(c) and the gradient of the line in Question E2(d).
Answer E4
Gradient of the line 2x + 3y = −5 is $-\dfrac23$; intercept is $-\dfrac53$
Gradient of the line x + y = −2 is −1.
(Reread Section 2 if you had difficulty with this question.)
Question E5 (A3)
A line ax + by − c = 0, with a ≠ 0 and b ≠ 0 meets the x– and y–axes at the points A and B, respectively.
(a) Find the area of the triangle AOB (where O is the origin)
(b) Find the length AB
(c) Find the shortest length h from the line to the origin O. [Hint: The shortest line will be perpendicular to AB, and what is the area of the triangle AOB when AB is the base?]
(d) Find the coordinates of the point N where the line y = 2 meets the line x = 5
(e) If we make a change to the coordinate system by putting
X = x − 5 and Y = y − 2
What are the new coordinates of the point N (in the XY system)?
(f) We can find the equation of the line AB in the new coordinate system if we put
x = X + 5 and y = Y + 2
into the equation ax + by − c = 0. What does this equation become?
(g) What is the shortest distance from the point (5, 2) to the line ax + by − c = 0?
Answer E5
(a) If y = 0 then $x = \dfrac ac$, and if x = 0 then $y = \dfrac cb$.
The points A and B are (c/a, 0) and (0, c/b) respectively. The area of the triangle AOB is therefore $\left\lvert\,\dfrac{c^2}{2ab}\,\right\rvert$ (allowing for the fact that a or b may be negative).
(b) The length AB is $\sqrt{\dfrac{c^2}{a^2}+\dfrac{c^2}{b^2}} = \lvert\,c\,\rvert\sqrt{\dfrac{1\os}{a^2}+\dfrac{1}{b^2}}$ (allowing for the fact that c may be negative).
(c) If we calculate the area of the triangle, with AB as the base and height h, we find $\dfrac{h\,\lvert\,c\,\rvert}{2}\sqrt{\dfrac{1\os}{a^2}+\dfrac{1}{b^2}} = \left\lvert\,\dfrac{c^2}{2ab}\,\right\rvert$
which can be rewritten as $h = \dfrac{1}{\sqrt{a^2+b^2}}$
(d) The line y = 2 meets the line x = 5 at the point N(5, 2).
(e) The point N becomes the origin X = 0, Y = 0.
(f) The equation of the line in the (X, Y) coordinate system is
a (X + 5) + b (Y + 2) − c = 0
which can be rearranged into the form aX + bY − (−5a − 2b + c) = 0 which is an equation of exactly the same type as before except that c has been replaced by C = (−5a − 2b + c).
(g) This transformation moves the point N, and the line AB, −5 units in the x–direction and −2 units in the y–direction so that N becomes the origin. The shortest distance from the point to the line remains unchanged. We can use the result that we obtained before: $h = \dfrac{\left\lvert\,C\,\right\rvert}{\sqrt{a^2+b^2}}$ and put
C = (−5a − 2b + c) to obtain $h = \dfrac{\lvert\,5a + 2b - c\,\rvert}{\sqrt{a^2+b^2}}$
(Reread Subsection 2.5Subsections 2.5 and Subsection 3.23.2 if you had difficulty with this question.)
Question E6 (A3 and A4)
Which of the lines 2x + 3y = 2 or 2x − 3y = 2 is perpendicular to the line 6x + 4y = 5? Find the equation of the line perpendicular to the line 6x + 4y = 5 which passes through the point (4, 4).
Answer E6
Gradient of the line 2x + 3y = 2 is $-\dfrac23$
Gradient of the line 2x − 3y = 2 is $\dfrac23$
and the gradient of the line 6x + 4y = 5 is $-\dfrac64 = -\dfrac32$
The product of gradients should be −1 for perpendicularity. Hence the line 6x + 4y = 5 is perpendicular to 2x − 3y = 2.
Any perpendicular to the line 6x + 4y = 5 has the equation $y = \dfrac23x+c$
Since it passes through the point (4, 4) then $4 = \dfrac83 + c$
Hence $c = \dfrac43$ and the equation is $y = \dfrac23x + \dfrac43$
(Reread Subsection 2.5 if you had difficulty with this question.)
Question E7 (A5)
Write down the equations of the circles of radius 3 which have centres at (1, −2) and (2, 1), respectively, and find where they meet.
Answer E7
The equations of the circles are
(x − 1)2 + (y + 2)2 = 9(i)
and(x − 2)2 + (y − 1)2 = 9(ii)
Expanding the equations we obtain
x2 − 2x + y2 + 4y = 4(iii)
andx2 − 4x + y2 − 2y = 4(iv)
Subtracting these equations we see that the required solution lies on the line
x = −3y(v)
Substituting for x from Equation (v) into Equation (i), we find
(3y + 1)2 + (y + 2 )2 = 9
i.e.5y2 + 5y − 2 = 0
Solving this quadratic equation we obtain
$y = \dfrac{-5\pm\sqrt{25+40\os}}{10} = \dfrac{-5\pm\sqrt{65\os}}{10}$
then substituting these values for y into (v) we obtain the points of intersection (−0.9187, 0.3062) and (3.9187, −1.3062).
(Reread Subsection 3.1 if you had difficulty with this question.)
Question E8 (A6)
Find the point of intersection of the tangents to the circle x2 + y2 = 4 at the points (1, $\sqrt{3\os}$) and (0, −2).
Answer E8
The tangent to the circle at (x1, y1) is x1x + y1y = 4
At (1, $\sqrt{3\os}$) this becomes x + $\sqrt{3\os}$y = 4, while at (0, −2) it becomes −2y = 4, i.e. y = −2
These meet where x − 2$\sqrt{3\os}$ = 4, i.e. x = 4 + 2$\sqrt{3\os}$
Intersection point is therefore (4 + 2$\sqrt{3\os}$, −2).
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E9 (A7 and A8)
Show that the points (1,2,1), (2,−3,−2) and (−1,0,−5) lie on the plane 2x + y−z = 3. Which two are the closest together?
Where does the line $\dfrac{x-1}{3}= \dfrac{y-1}{5} = \dfrac z2$ meet the plane 2x + y − z = 3?
Answer E9
Substituting (1, 2, 1) into the equation of the plane we find (2 × 1) + (1 × 2 ) − (1 × 1) = 3 so that the point does indeed lie in the plane.
Similarly for (2, −3, −2), (2 × 2) + (1 × (−3)) − (1 × (−2)) = 3
and for (−1, 0, −5), (2 × (−1)) + (1 × 0 ) − (1 × (−5)) = 3
Distance between first two = $\sqrt{\smash[b]{(-1)^2+5^2+3^2}} = \sqrt{35\os}$
Distance between last two = $\sqrt{\smash[b]{3^2+(-3)^2+3^2}} = \sqrt{27\os}$
Distance between first and last = $\sqrt{\smash[b]{2^2+2^2+ 6^2}} = \sqrt{44\os}$
The last two points are the closest together.
Rewriting the equations of the line in the form x = 1 + 3s, y = 1 + 5s and z = 2s and substituting into the equation of the plane we obtain 2 × (1 + 3s) + (1 + 5s) − (2s) = 3 from which we see that s = 0, and therefore the point of intersection is (1, 1, 0).
(Reread Section 4 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 5Closing items.