MATH 2.1: Introducing geometry |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
You may very well have met some of the concepts discussed in this module before; in fact it is hardly conceivable that you have not. Nevertheless there are many geometric terms which are in general use among physicists but which are commonly omitted from the standard school syllabus. The main aim of this module is to remedy that deficiency.
Geometry is of importance to all scientists and engineers since it deals with the relationships between points and lines, and with a variety of shapes in two and three dimensions.
In Section 2 of this module we examine straight lines and the angles between them, and then the shapes, such as triangles and rectangles, which can be formed by straight lines. Such concepts are fundamental to the study of physics and engineering, for example:
- It is well known in the study of optics that ‘the angle of incidence is equal to the angle of reflection’.
- Parallel lines drawn on a flat surface do not meet, and, if another line is drawn to intersect a pair of parallel lines, certain angles are formed which are equal.
- The simplest shape formed by straight lines is a triangle, but, in spite of being simple, such shapes are very important to the engineer because they form the simplest rigid structure.
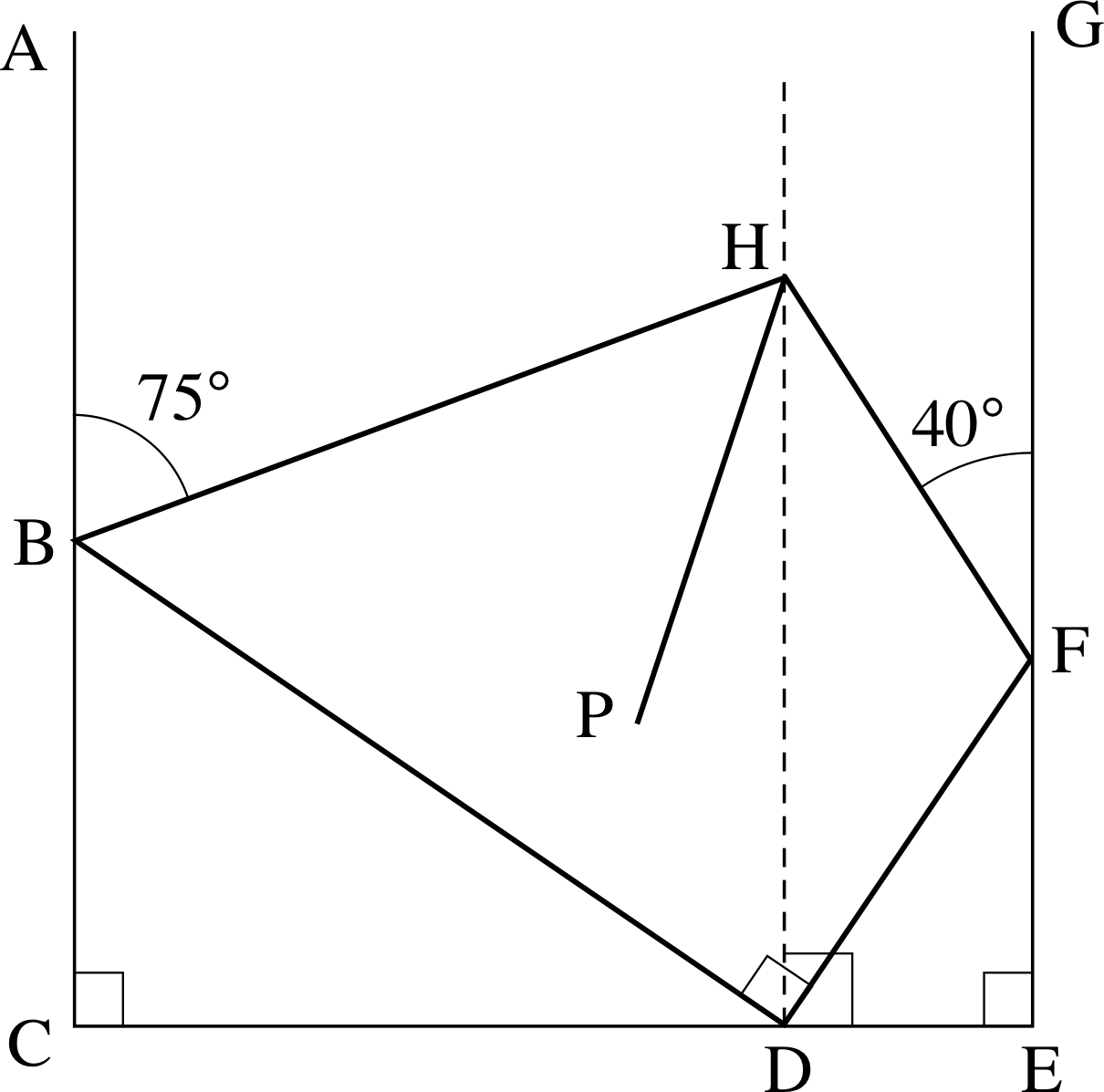
Figure 1 See Questions F1 and F2.
In Subsection 3.1 we discuss congruence, which, very roughly speaking, means that if you cut two congruent shapes from paper, then one will fit exactly over the other. In Subsection 3.2 we introduce similarity, and again speaking roughly, this means that one shape is a scaled version of the other (for example, the same shape but twice as big). In Section 4 we examine circles, and, in particular, the important concepts of radian measure and tangent lines. Finally in Section 5 we discuss the areas and volumes of various standard shapes.
Before we begin the module we should give you a word of warning. If you glance at Figure 1 you will see that the lines HF and DF appear to be approximately the same length. However in this topic equality means ‘exactly equal’ and not ‘approximately equal’. It is very easy to assume that because two lines in a figure look the same length they are the same length, and similarly for angles. In this subject you are either told that two lengths are equal or you deduce that they are equal from the given information. There is no other way!
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 6.1Module summary and the Subsection 6.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 6.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
In Figure 1 the line HP bisects the angle BH^F. Find the value of angle PH^D.
Answer F1
DH^F = HF^G = 40° (these are alternate angles)
BH^D = AB^H = 75° (these are alternate angles)
BH^F = BH^D + DH^F = 115°, so PH^F = ½ × 115° = 57.5°.
Since PH^D + DH^F = PH^F, it follows that PH^D = 57.5° − 40° = 17.5°.
Question F2
Again in Figure 1, BC^D = BD^F = DE^F = HD^E = 90°, and BD = 15 m, DF = 5 m, CE = 15 m, DE = 3 m.
Show that the triangles BCD and DEF are similar, and hence find the lengths of EF and BC.
Answer F2
BD^C + BD^F + FD^E = 180° (angles on a straight line)
∴ BD^C + FD^E = 90°. (The symbol ∴ is often used for ‘therefore’.)
But FD^E + DF^E = 90° and ∴ DF^E = BD^C.
Hence CB^D = FD^E and it follows that the triangles BCD and DEF are similar.
We have $\rm \dfrac{BC}{DE} = \dfrac{DB}{FD}$, so that BC = (15 × 3/5) m = 9 m.
Also$\rm \dfrac{EF}{CD} = \dfrac{FD}{DB}$, so that
$\rm EF = \dfrac{FD}{DB}\,CD = \dfrac{FD}{DB}\,(CE-DE) = 5(15-3)\,m = 4\,m$
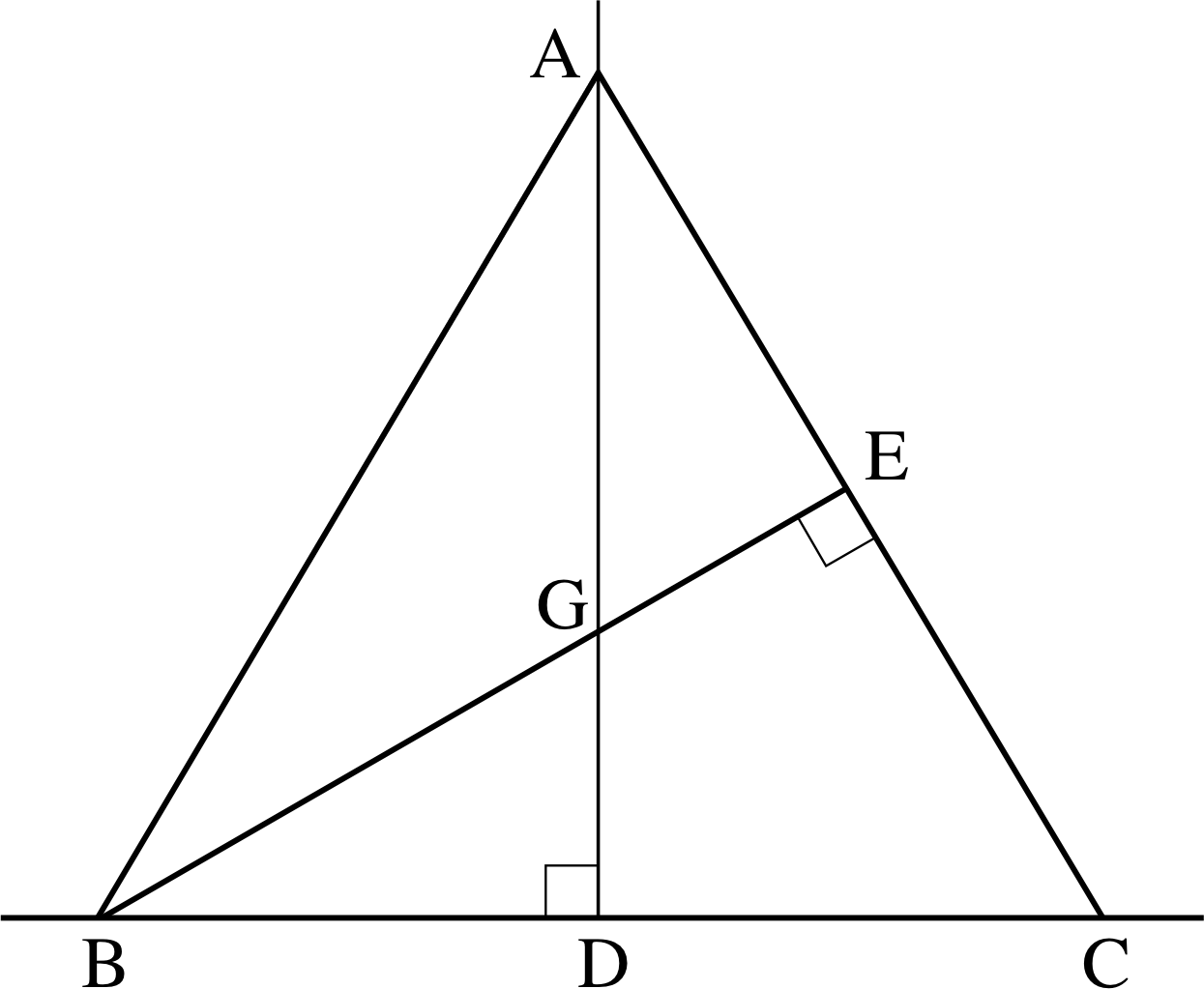
Figure 2 See Question F3.
Question F3
In Figure 2, AC = BC and BE^C = AD^C = 90°. By calculating the area of the triangle ABC using two different methods, or otherwise, show that BE = AD. Hence show that the triangles BEC and ADC are congruent.
Answer F3
Area of triangle ABC = ½ BC × AD = ½ AC × BE, but AC = BC and therefore AD = BE. It follows that triangles ADC and BEC are congruent (see (d) in the four minimal specifications for unique triangles in Subsection 3.1).
Question F4
A steel pipe is 10 m long. Its inside diameter is 40 mm and its outside diameter is 50 mm. Calculate the volume of the steel in m3.
Answer F4
The cross–sectional area of the pipe wall is the difference between the areas of the circles of diameter 50 mm = 0.05 m and diameter 40 mm = 0.04 m,
i.e.$\rm \pi\left(\dfrac{0.05\,m}{2}\right)^2 - \pi\left(\dfrac{0.04\,m}{2}\right)^2 = (6.25 - 4.0) \times 10^{-4}\pi\,m^2$
The volume is 10 m × (6.25 − 4.0) × 10−4π m2 = 2.25 × 10−3π m2 ≈ 7.069 × 10−2 m2.
(Notice how it is often easier to convert all the lengths into the appropriate units before calculating the volume.)
1.3 Ready to study?
Study comment In order to study this module you will need to be familiar with the following terms: angle, line, two dimensional and three dimensional. If you are uncertain of any of these terms you can review them now by referring to the Glossary which will indicate where in FLAP they are developed. In addition, you will need to be familiar with SI units. It is also assumed that you can carry out basic algebraic and arithmetical manipulations (see algebra in the Glossary), in particular calculations using indices. You will also need a ruler (measuring centimetres), a protractor and a pair of compasses. The following questions will allow you to establish whether you need to review some of the topics before embarking on this module.
Question R1
(a) If $\dfrac xy = \dfrac zw$ and y = 6, z = 15, w = 10, find x.
(b) Given that $\dfrac xy = \dfrac yz$, x = 6 and z = 24, find the possible values of y.
(c) Given that x3 = 5, calculate the value of x2.
Answer R1
(a) Substituting the given values into the equation gives us $\dfrac{x}{6} = \dfrac{15}{10}$.
If we then rearrange this we obtain $x = \dfrac{6 \times 15}{10} = \dfrac{90}{10} = 9$.
(b) If we multiply the given equation by yz, we find $\dfrac{x}{y} \times yz = \dfrac{y}{z} \times yz$, i.e. xz = y2.
Ifx = 6 and z = 24 then y2 = 6 × 24 = 144, from which we calculate y = ± $\sqrt{144\os}$ = ±12.
(c) x = 51/3 and therefore x2 = 52/3 ≈ 2.924.
Question R2
Draw a line AB of length 7 cm, then, using a pair of compasses, draw a circle centre A of radius AB and a circle centre B of radius AB. Label the points at which the circles intersect as P and Q, then draw the line PQ and label as M the point where it meets the line AB. Use a protractor to measure the angle between the two lines (PQ and AB), then use a ruler to measure AM and MB in cm. Use your protractor to measure the angle between the lines PA and PB, and then the angle between the lines PA and QA.
Answer R2
The lines PQ and AB meet at right angles (90°) at the mid–point M of AB (so that AM = MB = 3.5 cm). The angle between PA and PB is 60° while the angle between PA and QA is 120°.
2 Euclidean plane geometry i
2.1 Lines and angles
The most fundamental geometric concept is that of a point, which occupies a position but has no size or dimension. Initially we will be concerned with points that lie on a flat surface (like this sheet of paper), usually called a plane surface or, more simply, a plane. We will also investigate the properties of lines drawn on the plane. A line has length as its sole dimension, but it has no thickness. Of course, these are theoretical concepts; in practice, when we plot a point or draw a line we have to give it thickness in order to be able to see it.
A straight line is the shortest distance between two points. It is the path traced out by moving from one point to the other in a constant direction. If we wish to be precise then we would have to allow the straight line to extend infinitely away from any point on it and define that part of it between two particular points as a straight line segment. Any two points on the plane can be joined by a unique straight line segment which lies entirely in the plane. i We say that two lines intersect if they have a point in common, known as the intercept (if they have more than one point in common then they must be identical because of the uniqueness property of straight lines). Two lines that do not intersect are said to be parallel. That part of a straight line which extends from a given point in one direction only is called a ray – you may have heard of the term ‘a ray of light’.
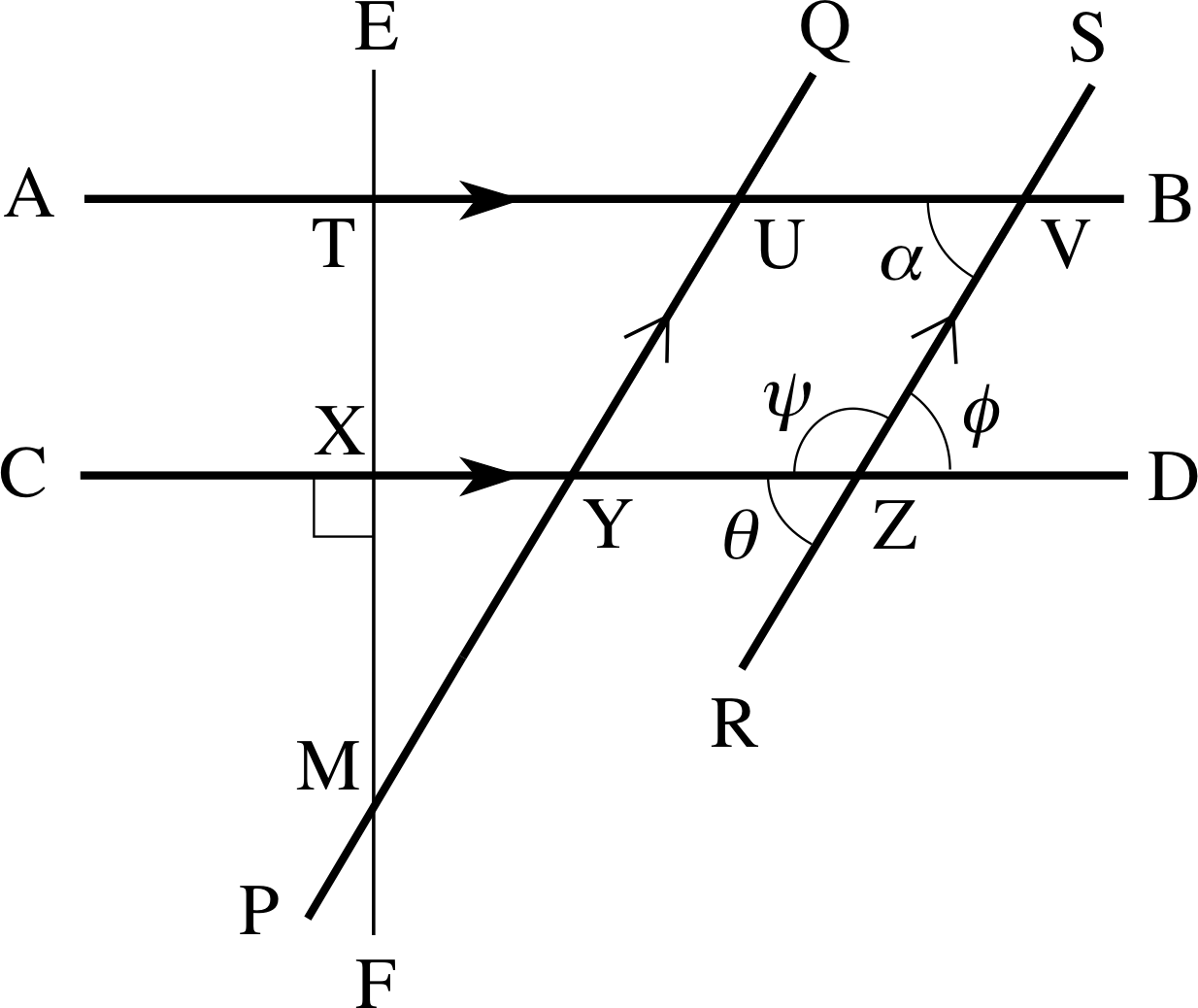
Figure 3 Properties of parallel lines.
Figure 3 is intended to illustrate a number of important concepts. First, the two lines YD and RV intersect at the point Z; of course the lines are not depicted in full (they are infinite in extent, after all) but by segments. The points C and X also lie on the line YD, and we say that they lie on the line DY produced. i
There are four angles formed by the two lines YD i and RV: YZ^V, VZ^D, DZ^R and RZ^Y. The notation is fairly obvious, the caret (^) sign is placed over the letter representing the point of the angle. It is also common practice to denote angles by letters (often Greek letters), so that in this case YZ^R = θ (the Greek letter theta). An angle is a measure of the rotation from one ray to another, for example from ZV to ZD. To quantify this rotation we measure a full rotation (i.e. one that gets you back to where you started) by 360 units, called degrees, written 360°. Hence turning the ray ZV first to ZD, then ZR, then ZY and finally on to its starting point, is a rotation of 360°. When the four angles are equal to each other, and therefore each is equal to 90°, the lines are said to be perpendicular to each other or to intersect at right angles. This is the case for the lines EF and CD intersecting at X. Notice the symbol (a box) used at X to denote a right angle.
The angles θ and ψ (the Greek letter psi) together form half a complete turn about the point Z, and so their sum must be 180°. This is also the case for the angles ψ and ϕ (phi), and it follows that θ = ϕ. The angles θ and ϕ are said to be vertically opposite, and we have just shown that vertically opposite angles must always be equal.
✦ In Figure 3, if UV^Z = 50° what are the values of the three other angles at V?
✧ SV^B = 50° (UV^Z and SV^B are vertically opposite angles and therefore equal.)
UV^S = BV^Z = 130° (UV^Z and UV^S form half a complete turn, while UV^S and BV^Z are vertically opposite.)
Angles less then 90° are called acute angles, those greater than 90° and less then 180° are obtuse angles, and those greater than 180° and less than 360° are reflex angles.
✦ Classify the angles 135°, 60°, 250°, 310°, 90°.
✧ Obtuse, acute, reflex, reflex, right angle.
When two angles add up to 180° they are said to be supplementary_anglessupplementary; when they add up to 90° they are complementary_anglescomplementary.
✦ What are the angles that are supplementary to 130°, 60°, 90°? What are the angles that are complementary to 30°, 45°, 60°, 90°?
✧ The supplementary angles are 50°, 120°, 90°.
The complementary angles are 60°, 45°, 30°, 0°.
2.2 Parallel lines
Parallel lines are indicated by arrowheads, as in Figure 3, and notice that different pairs of parallel lines are indicated by arrowheads of different styles. A line which intersects two parallel lines is called a transversal, so that (in Figure 3) RS is a transversal to the pair of parallel lines AB and CD. When two parallel lines are intersected by a transversal two sets of equal angles are created.
The angles θ and α (the Greek letter alpha) in Figure 3 are equal; they are corresponding angles – they occur on the same side of the transversal. The angles ϕ and α are equal; they are alternate angles – they occur on opposite sides of the transversal.
✦ In Figure 3 PQ and RS are parallel lines and AB is a transversal.
(a) Identify the corresponding angle to α that occurs at point U.
(b) Identify which angle at V is vertically opposite to α.
(c) Give an example of two angles at U that are supplementary.
(d) Identify which angle at U is alternate to α.
✧ (a) TU^Y, (b) SV^B, (c) TU^Y and TU^Q (or TU^Q and QU^V, or QU^V and VU^Y, or VU^Y and TU^Y), (d) QU^V.
2.3 Triangles
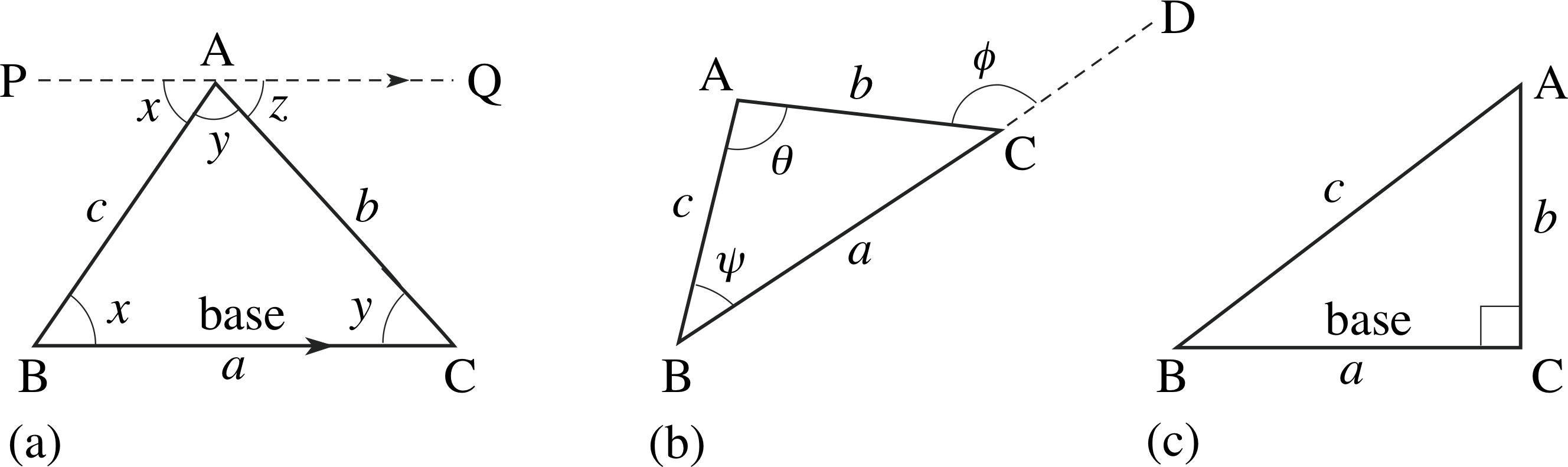
Figure 4 Various types of triangle.
A triangle is a closed figure which has three sides, each of which is a straight line segment. A triangle is usually labelled with a capital letter at each of the corners which are more properly known as the vertices (the plural of vertex). We speak of the triangle ABC, for example.
Figure 4 shows three types of triangle (for the moment you can ignore the dotted lines and labelled angles).
In each of the three triangles the angles BA^C, AC^B and CB^A are known as the interior angles of the triangle (and sometimes referred to as the angles A^, B^ and C^, or even more briefly as the angles A, B and C). Note that:
- In Figure 4a all the interior angles are acute.
- In Figure 4b one of the angles, A, is obtuse.
- In Figure 4c one of the angles, C, is 90°, i.e. a right angle.
Notice that we have also introduced the notation of a lower–case letter to represent each side of a triangle, the side a is opposite the angle A, and so on.
In the case of Figures 4a and 4c it is natural to refer to the side BC as the base of the triangle, however any side may be regarded as the base – it just depends on how you want to view it.
If all three sides of a triangle are equal (i.e. their lengths are equal) then the triangle is known as an equilateral triangle and it is a consequence of this definition that the angles are equal. It is also the case that if the angles are equal then so are the sides.
If two sides of the triangle are equal the triangle is said to be isosceles_triangleisosceles, and the interior angles at either end of the third side are equal. A triangle for which one of the interior angles is a right angle is called a right–angled triangle and the side of the triangle opposite to the right angle (i.e. the longest side) is called the hypotenuse. A triangle whose three sides are unequal is called scalene_trianglescalene.
An important result is that the sum of the interior angles of any triangle is 180°. i
In Figure 4a the dotted line PQ is drawn through the vertex A and parallel to the opposite side BC. In the figure we have marked a pair of equal alternate angles x and a pair of equal alternate angles z. The sum of the angles (at A) on a straight line is 180° and hence x + y + z = 180°, which proves the required result.
The angle ϕ in Figure 4b is called an exterior angle of the triangle.
✦ By drawing a ray from C in Figure 4b, parallel to BA, show that ϕ = θ +ψ.
✧ The angle between AC and the ray is an alternate angle to θ, and the angle between the ray and CD is a corresponding angle to ψ. It follows that the exterior angle (ϕ ) is equal to the sum of the opposite interior angles (θ and ψ). This result is true in general, and worth remembering.
There is an alternative proof of the fact that the interior angles of a triangle sum to 180° which is worth mentioning since the same method can be applied very easily to figures with more than three sides.
Imagine that you are standing at B in Figure 4b and that you walk along the side BC until you reach C. You now turn anticlockwise through the angle ϕ until you are facing A; in other words you turn through an angle (180° − C). i Now continue along CA until you reach A, where you turn anticlockwise through an angle (180° − A). Finally you proceed along AB until you reach B, then turn anticlockwise through an angle (180° − B) so that you have returned to your starting point and you are facing in your original direction, which means that you have made a complete turn of 360°. However this complete turn was composed of three exterior angles, so that
(180° − A) + (180° − B) + (180° − C) = 360° and therefore A + B + C = 180°.
Question T1
Use an argument similar to the above to show that the sum of the interior angles of a four–sided figure (such as a square) is 360°.
Answer T1
The argument is identical to that for the triangle except that there are now four vertices, and therefore four anti–clockwise turns. Letting A, B, C and D denote the four interior angles, it follows that
(180° − A) + (180° − B) + (180° − C) + (180° − D) = 360°
and therefore A + B + C + D = 360°.
Pythagoras’s theorem
The sides of a right–angled triangle are related in a particularly simple fashion, and the following result, using the notation of Figure 4c, is known as Pythagoras’s theorem
c2 = a2 + b2(1)
where c is the longest side, i.e. the hypotenuse. We state the theorem without proof. i
✦ Given that a = 0.8 cm and c = 1.7 cm in Figure 4c, calculate the value of b.
✧ Since b2 = c2 − a2 it follows that b2 = 2.25 cm2 and therefore b = 1.5 cm.
It should be noted that any triangle with sides of lengths a, b and c that satisfies Pythagoras’s theorem must be a right–angled triangle. Thus, even if the only thing you know about a triangle is that its sides are of lengths 3 units, 4 units and 5 units you can still be sure that it is a right–angled triangle simply because 32 + 42 = 52. Other well known sets of numbers that satisfy a2 + b2 = c2 are 5, 12, 13 and 6, 8, 10.
✦ Is a triangle with sides 9 m, 12 m, and 15 m a right–angled triangle?
✧ Yes. You can show this by checking that the values satisfy a2 + b2 = c2, or more simply by noting that if you express the given lengths as multiples of 3 m ‘units’ the sides are of length 3 units, 4 units and 5 units.
2.4 Polygons

Figure 3 Properties of parallel lines.
Quadrilaterals
Any closed geometric shape whose sides are straight line segments is called a polygon. We have already met a three–sided polygon – a triangle. Four–sided polygons are known as quadrilaterals. When all the sides of a polygon are equal it is, not surprisingly, called an equilateral polygon; if all the internal angles are equal it is equiangular; and a polygon that is both equilateral and equiangular is said to be regular_polygonregular. i Thus, for example, a regular quadrilateral is just a square. The perimeter of a polygon is the sum of the lengths of the sides.
A parallelogram is a special case of a quadrilateral in which the opposite sides are parallel (as, for example, UVZY in Figure 3).
✦ Imagine a line drawn from U to Z in Figure 3. Is the triangle UVZ necessarily isosceles?
✧ No. We cannot be sure that UV = VZ.
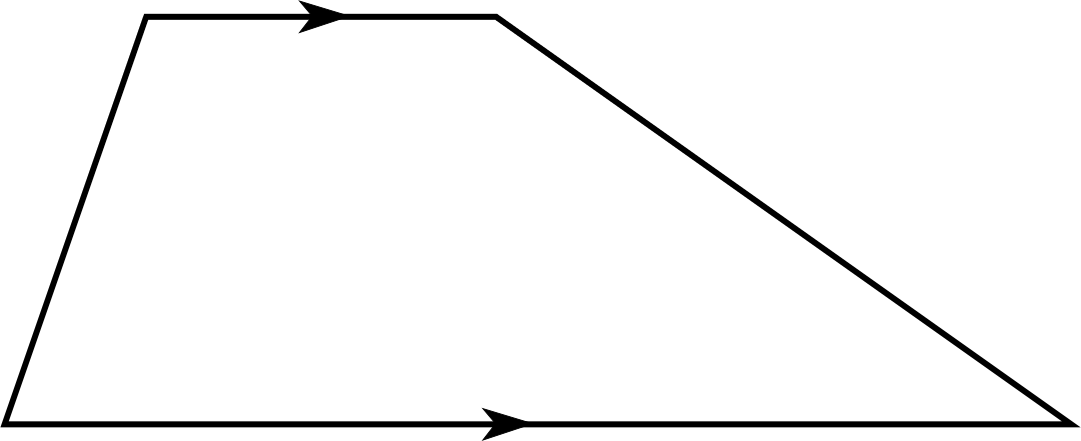
Figure 5 A trapezium.
A parallelogram with all sides equal in length is called a rhombus, popularly known as diamond-shaped.
If the internal angles of a parallelogram are each 90° then the quadrilateral is a rectangle, if the sides are also equal in length then the rectangle is a square.
A quadrilateral in which one pair of opposite sides is parallel is known as a trapezium (see Figure 5).
✦ Is every rectangle a square? Is every square a rectangle? Is every rectangle a rhombus? Is every square a rhombus?
✧ Every square is a rectangle, but not all rectangles are squares. Not every rectangle is a rhombus, but every square is a rhombus.
General polygons
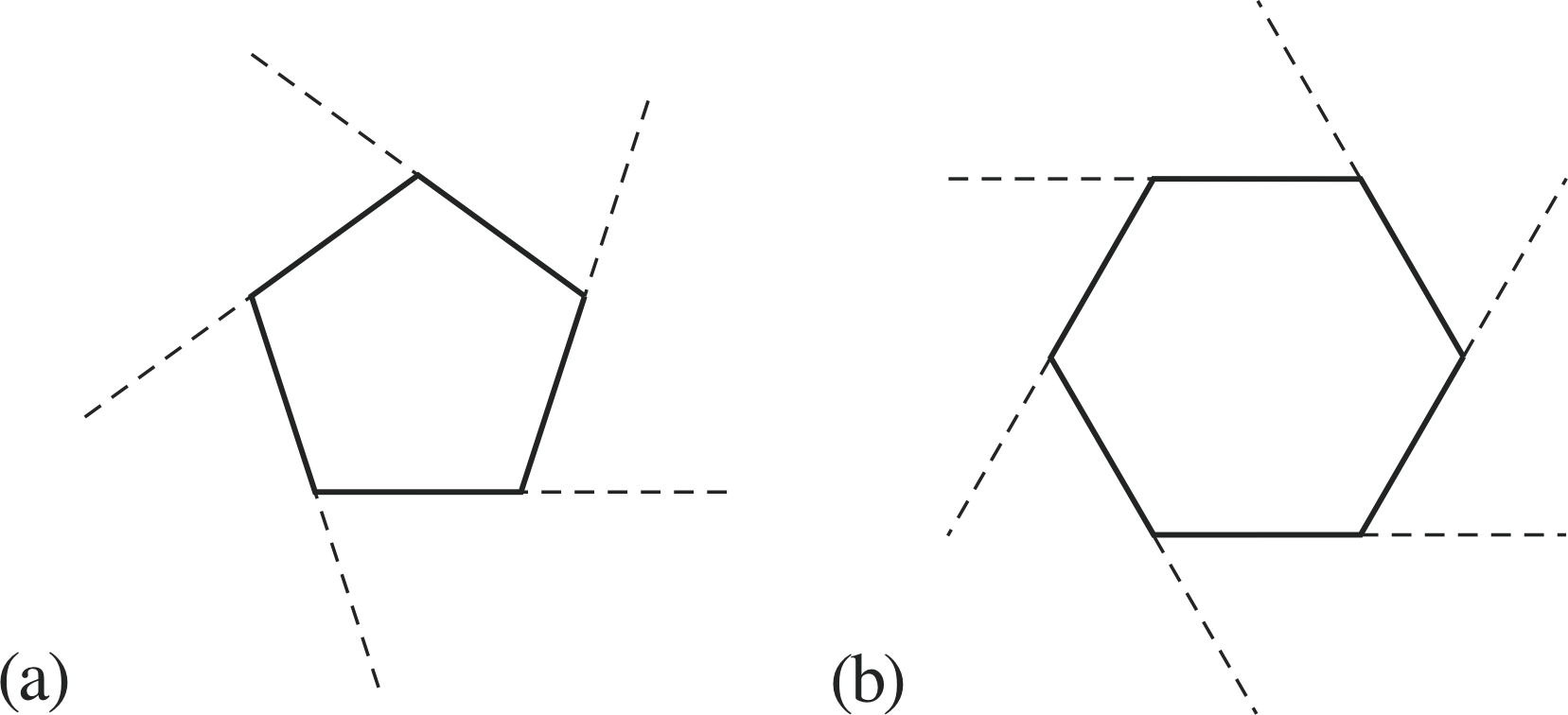
Figure 6 (a) A regular pentagon, and (b) a regular hexagon.
Although triangles and quadrilaterals are the most commonly occurring polygons, the following result is sometimes useful since it can be applied to polygons with any number of sides. i As one would expect, the corners of a polygon are known as vertices_of_a_polygonvertices and the angle formed at a vertex which lies in the interior of the polygon is called an interior angle. The method that we used to show that the sum of the interior angles of a quadrilateral is 360° can easily be adapted to show that:
The sum of the interior angles of an n sided polygon is (2n − 4) × 90°, i.e. (2n − 4) right angles.
Figure 6 shows a regular pentagon and a regular hexagon.
✦ What is the size of an interior angle in (a) a regular pentagon, and (b) a regular hexagon?
✧ (a) The sum of the interior angles in a pentagon is (10 − 4) × 90° = 540°, since there are five sides each interior angle in a regular pentagon is 15 (540°) = 108°.
(b) The sum of the interior angles in a regular hexagon is (12 − 4) × 90° = 720° so that each interior angle is $\frac16$ (720°) = 120°.
3 Congruence and similarity
3.1 Congruent shapes
Geometric figures which are the same shape and size are said to be congruent. If we were to cut congruent triangles out of a piece of paper, we would be able to fit one exactly on top of the other, though we might have to turn one over or rotate it to do so. It is very important to be able to decide when triangles are congruent and the main aim of this section is to discuss this question.
In order to decide whether triangles are congruent, we need to know what is the minimum information to specify completely a triangle of unique size and shape. All triangles drawn with such a specification will then be copies of each other, and so congruent. There are four possible ways to specify a triangle of unique size and shape. These are as follows:
Minimal specifications of a triangle i
(a) State the length of all three sides. (SSS)
(b) State the lengths of two sides and the angle between them. (SAS)
(c) State the length of one side and the angles at each end of it. (ASA) i
(d) Specify a right angle, the length of the hypotenuse and the length of one other side. (RHS)
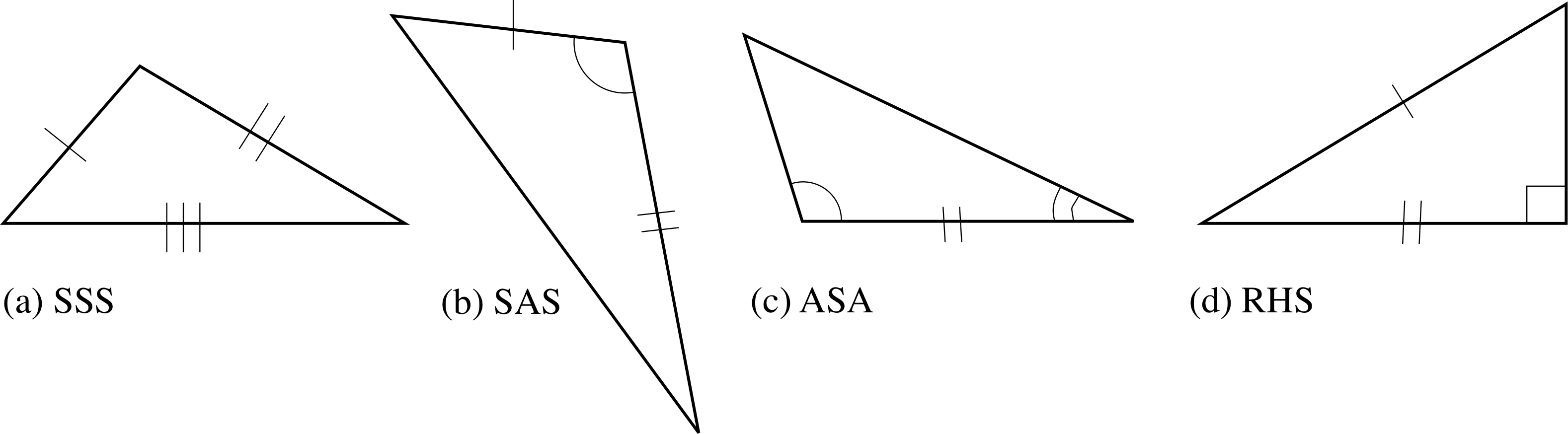
Figure 7 Minimal specifications for a triangle. The cross bars and angles indicate the sides and angles referred to in the specifications.
These specifications are shown diagramatically in Figure 7 together with abbreviations which may help you to remember them. The bars across the lines are often a useful device for indicating lines of equal length and in Figure 7 they indicate the lines referred to in the specifications above. We can now try to construct a triangle from each of these four specifications.
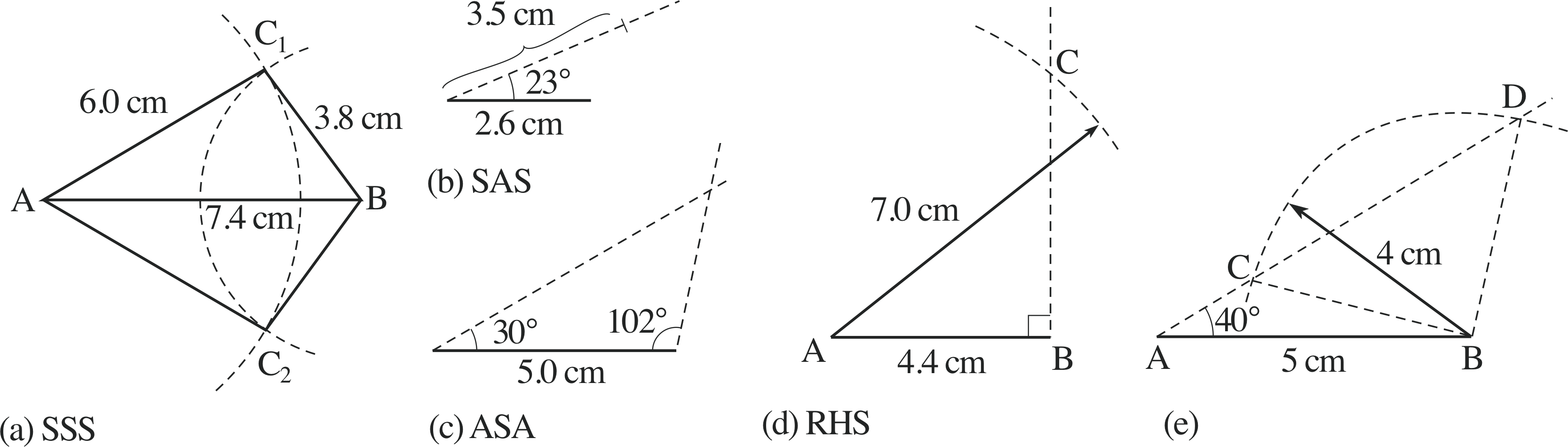
Figure 8 Constructing triangles using the minimal specifications. (These figures are not to scale.)
- (a)
-
Suppose that we are told that the lengths of the sides of a triangle are 7.4 cm, 6.0 cm and 3.8 cm. We first draw a line AB with the length of one of the sides, say 7.4 cm, as in Figure 8a. Then we draw a circle, i with its centre at A, with the length of another side, say 6.0 cm, as its radius. Finally we draw a second circle with B as centre and the length of the third side, 3.8 cm, as its radius. If the circles intersects at a point C1, then the triangle ABC1 has sides of the required lengths. (The other intersection, C2, would do equally well: triangle ABC1 is a mirror–image in the line AB of triangle ABC2).
- (b)
-
Suppose that we are told that the lengths of two of the sides of a triangle are 2.6 cm and 3.5 cm, and that the angle between them is 23°. First we draw a line segment of one of the known lengths, say 2.6 cm, as in Figure 8b. Next we use a protractor to draw a straight line through one end of this line segment and at the known angle, 23°, to it. We make the length of the second line the second known length 3.5 cm. Finally we join the end of the second line to the end of the first, giving the required triangle.
- (c)
-
Suppose that we are given the length of one side, say 5.0 cm, and the angles at either end of this line, say 30° and 102°. We first draw a line segment of the known length, 5.0 cm, which immediately gives us two vertices of the triangle, as in Figure 8c. Then from each vertex we draw a line at the specified angle to the line segment. The intersection of these two lines gives us the third vertex.
- (d)
-
Suppose that we are told that one of the angles in the triangle is a right angle and we are given the lengths of the hypotenuse and one other side, say 7.0 cm and 4.4 cm, respectively. We first draw a line segment the length of the given side other than the hypotenuse, AB in Figure 8d. Then we draw a line at right angles to it at one end, B say; finally, we draw a circle with its centre at the other end, A, and of radius equal to the length of the hypotenuse. The point at which this circle intersects the second line, C, is the third vertex of the triangle.
Three pieces of information are not always sufficient to specify a triangle completely. If we are given the lengths of two sides and an angle other than the one between the sides, it is possible that we will be able to draw two (non–congruent) triangles each meeting the given specification. For example, suppose we are told that a triangle has two sides of length 4 cm and 5 cm, and that the angle at the end of the 5 cm line (not between it and the 4 cm line) is 40°. We can construct two possible triangles (ABC and ABD), but they are not congruent with each other, as illustrated in Figure 8e.
✦ Would the three interior angles completely specify a unique triangle?
✧ No. There would be a free choice of the length of any one side.
Triangles like these which are of the same shape but of different sizes are called similar triangles and we will be discussing them in detail in the next subsection. Of course once the length of a particular side is chosen, you then have a side and the angle at each end of it specified, and so you can draw a unique triangle as in case (c) above.
Having determined the minimal amount of information needed to uniquely specify a triangle (the conditions SSS, SAS, ASA and RHS of the previous box), we can now present a simple test for the congruency of two triangles.
Test for congruent triangles
Two triangles must be congruent if the information contained in any of the conditions SSS, SAS, ASA or RHS is the same for both.
It should be noted that although the above test only requires one of the minimal specifications to be common to both triangles it must follow that if the triangles are congruent then common values can be found for all three of the general specifications (SSS, SAS, ASA) and for the fourth specification (RHS) if it applies.
Bisectors
Isosceles triangles have some useful properties arising from their symmetry.
In the triangle ABC of Figure 8a, AB = AC. The line AD is drawn so that BA^D = CA^D = ½ (BA^C). This line is called the bisector of the angle BA^C. The term is also applied to line segments, so that a point lying at the mid–point of a line segment is sometimes said to bisect the line segment.
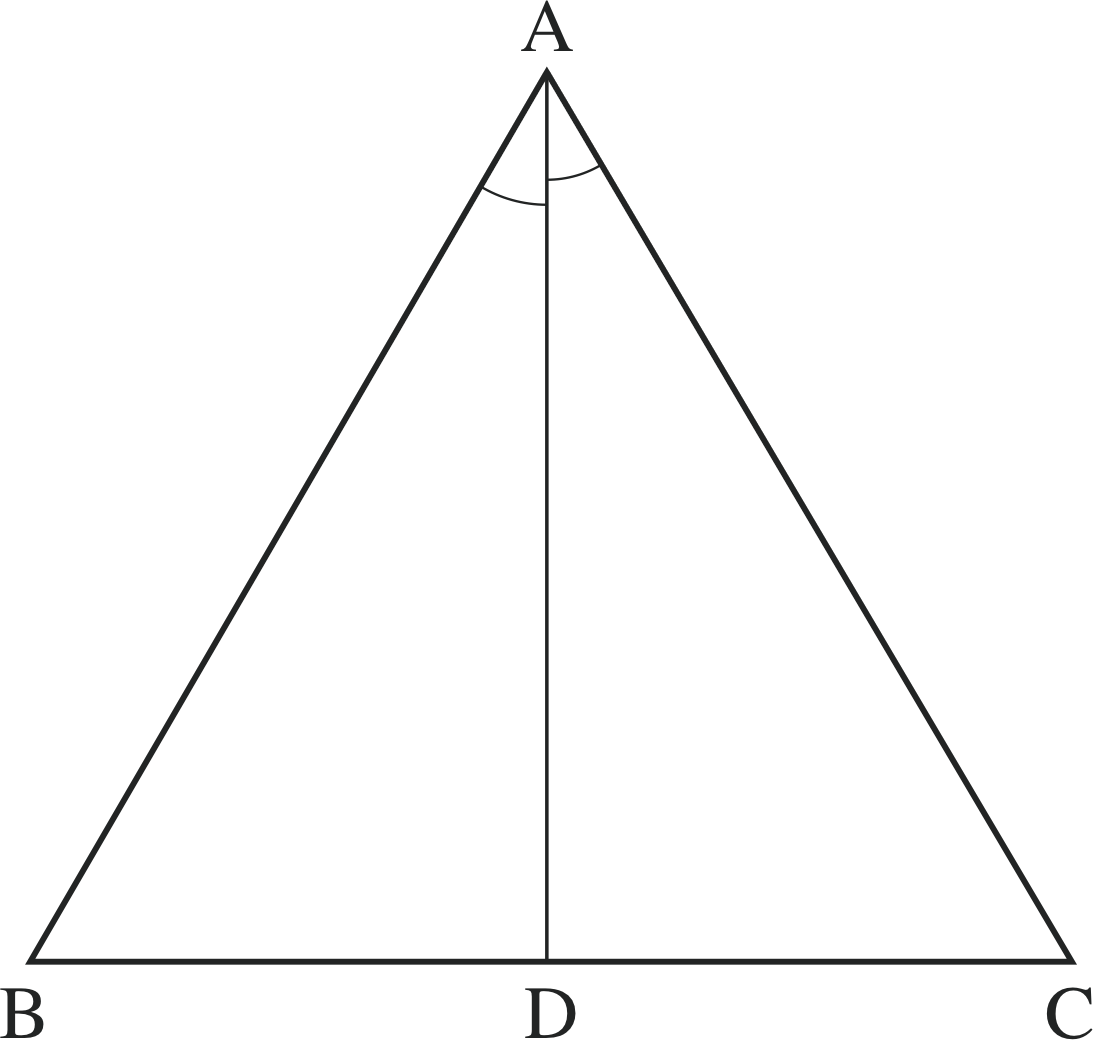
Figure 9 (a) See Question T2.
Question T2
By finding a pair of congruent triangles in Figure 9a, show that: (a) AB^C = AC^B, (b) AD^B = AD^C = 90°, (c) BD = CD.
Answer T2
Triangles ADB and ADC are congruent since they share a common side (AD), AB = AC and the angles BA^D and CA^D are equal. Hence the angles AB^C and AC^B are equal. Further, since angles AD^B and AD^C add up to 180° and are equal; their common value is 90°. Finally, the sides BD and CD must be of equal length.
The properties established in Question T2 are quite general for isosceles triangles and may be summarized as follows.
In any isosceles triangle:
(a) The angles opposite the equal sides are themselves equal.
(b) The line bisecting the angle between the equal sides also bisects the third side, and is perpendicular to it.
Question T3
Show that the angles in an equilateral triangle are of equal size, and find their magnitude.
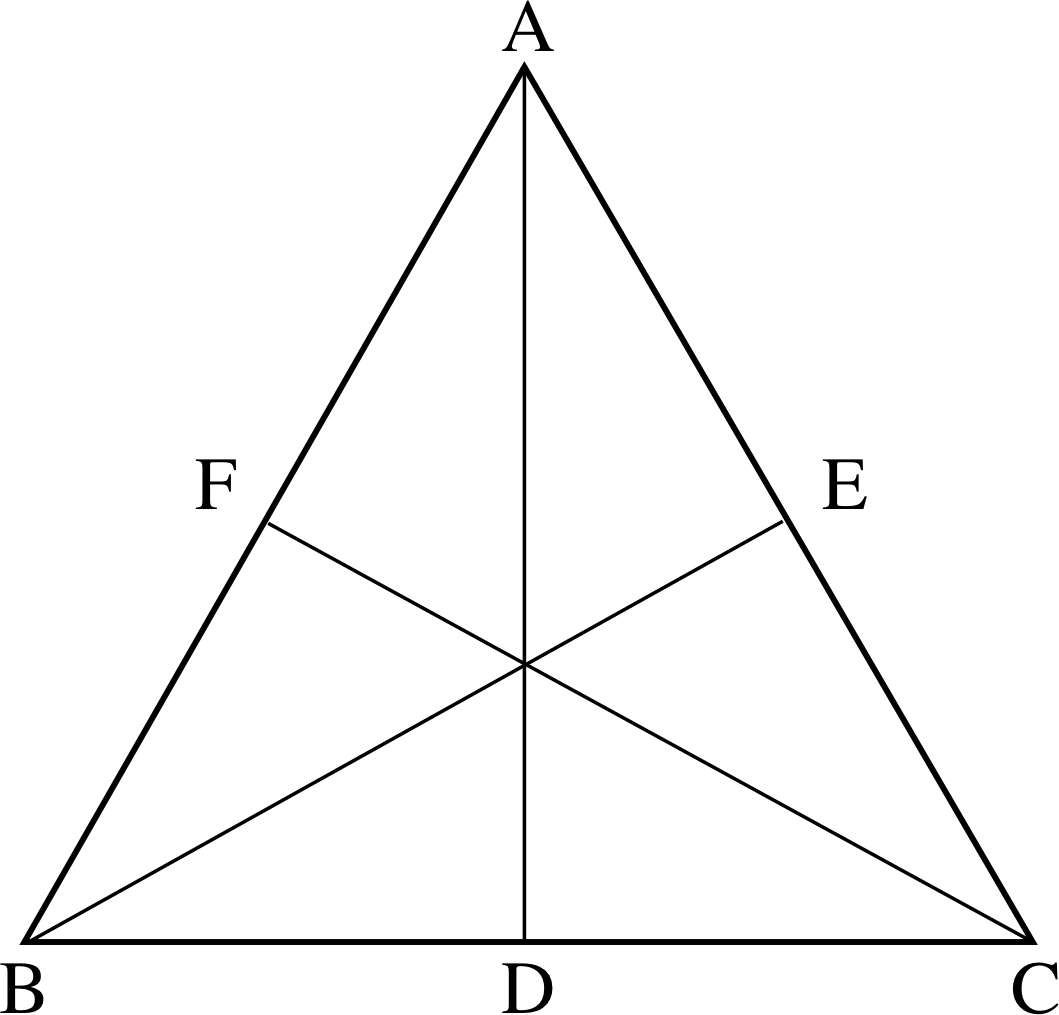
Figure 23 See Question T3.
Answer T3
Refer to Figure 23 in which ABC is an equilateral triangle. Since AB = AC the triangle is isosceles (with BC as base) and therefore AB^C = AC^B. Also AB = BC and so the triangle is isosceles (with AC as base) so that AC^B = BA^C. Hence the three angles AB^C, AC^B and BA^C are of equal size. Since they are the interior angles of a triangle their sum is 180°, and so each is equal to 60°.
A line which bisects a line segment and intersects it at right angles is called a perpendicular bisector of the line segment. Thus the line AD in Figure 9a is a perpendicular bisector of the side BC.
A median is a line drawn from one vertex of a triangle to the mid–point of the opposite side. Although it is not the case for all triangles, for an isosceles triangle the median, perpendicular bisector and the angle bisector are identical.
Figure 9 (b) See Question T4.
Question T4
In Figure 9b the line CM = AM and CM is a median so that AM = MB. Show that the angle AC^B is 90°.
Answer T4
In Figure 9b the triangles ACM and BCM are both isosceles so that CA^M = AC^M = x say, while M^CB = MB^C = y say. However, the angles in the triangle ABC sum to 180°, i.e. 2x + 2y = 180° and therefore AC^B = x + y = 90°$.
3.2 Similarity, ratios and scales
If two roads meet at an angle of 30°, we expect the same angle to occur on an Ordnance Survey map of the area, in other words we expect maps and plans to preserve the true angles. However, it would be ridiculous to construct a road map with the same dimensions as the original site, so map–makers and designers use the concept of scaling_of_a_geometric_figurescaling. Often a short distance on the map or plan represents a much longer distance in reality, but sometimes the reverse is true and a relatively large distance on the plan may represent a minute length in the real object (as, for example, in the plan of a circuit in a microchip). On one popular series of Ordnance Survey maps, 1 cm on the map represents 50 000 cm or 0.5 km on the ground so that 2 cm represent 1 km.

Figure 7 Minimal specifications for a triangle. The cross bars and angles indicate the sides and angles referred to in the specifications.
The essence of scaling is that it preserves shape. You have already come across this idea in Subsection 3.1. When two (or more) triangles are the same shape they are said to be similar triangles. The triangles shown in Figures 7b and 7c are actually similar (although it requires a rotation and a reflection of one of them to put them into the same orientation).

Figure 3 Properties of parallel lines.
If you look at Figure 3 you should be able to see that triangles MXY and MTU are also similar. You should note the convention used when discussing similar triangles, the order of the letters indicates the correspondence of the vertices. It is also true that any two congruent triangles are also similar. i
An important property of similar triangles is that corresponding sides are in the same ratio, i.e. they are scaled by the same factor. i
Suppose that in an Ordnance Survey map the scale is 2 cm to represent 1 km on the ground. We can express this scale as the ratio of the distance on the map to the corresponding distance on the ground, this ratio is then 1 : 50 000. In other words, actual distances are reduced by a factor of 50 000 before they are drawn on the map. The essential point is that only one scale is used for all distances in all directions (even curved paths).
Figure 10 Similar triangles.
If A, B and C in Figure 10 represent the positions of three towns, and P, Q and R are their respective positions on the map, then
$\rm PQ = \dfrac{AB}{50\,000}\quad QR = \dfrac{BC}{50\,000}\quad RP = \dfrac{CA}{50\,000}$ i
It follows that
$\rm \dfrac{PQ}{AB} = \dfrac{QR}{BC} = \dfrac{RP}{CA}$
In any two similar triangles the ratios of corresponding sides are equal, and this result is true whatever the scale.
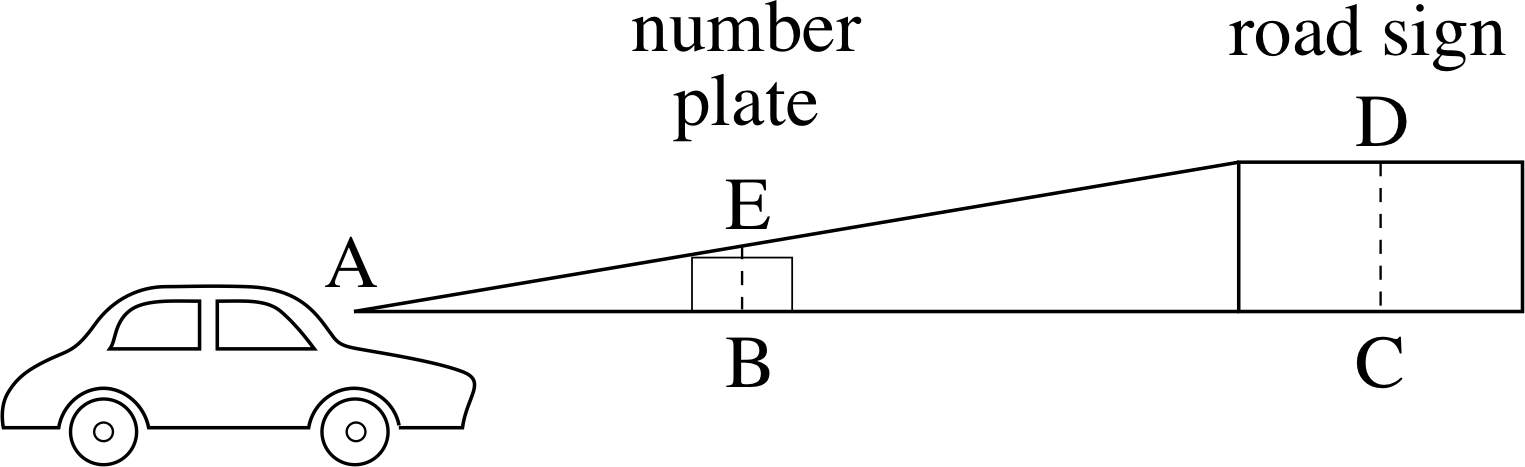
Figure 11 See Question T5.
Question T5
Drivers are expected to be able to read car number plates at a distance of about 25 metres. The letters on the number plates are 8 cm high. You wish to put up a road sign which drivers travelling at 30 m s−1 will be able to read with ease. If it takes 3 s to read what is on the sign, and the driver must have completed reading it 100 m before the car reaches the sign (so that the driver can respond to what she/he reads), how large should you make the lettering on the road sign? This is illustrated in Figure 11.
Answer T5
Refer to Figure 11. In 3 s the driver travelling at 30 m s−1 would have travelled about 90 m hence the lettering on the sign should be capable of being read first at a distance of 190 m so AC = 190 m. The driver can read a number plate at 25 m so that AB = 25 m. Assuming that what matters is the angle that the eye is scanning (i.e. we assume that focusing is not a problem), we need to ensure that to the driver CD appears to be the same height as EB (a number plate). Since angles EA^B and DA^C are equal, and EB and DC are both vertical, triangles ABE and ACD are similar.
Hence$\rm \dfrac{DC}{EB} = \dfrac{AC}{AB}$
therefore$\rm DC = EB\times\dfrac{AC}{AB} = \left(8\times10^{-2}\times\dfrac{190}{25}\right)\,m \approx 6\,cm$
Similar triangles and shadows
Now suppose that in Figure 10, AC represents a tree while AB represents the shadow cast by the tree; RP is a measuring pole of length 1 m and PQ represents its shadow. Suppose that we measure the length of the shadows and find them to be AB = 3.0 m and PQ = 0.75 m, we can then use the fact that ABC and PQR are similar triangles to calculate the height of the tree. Since the triangles are similar,
$\rm \dfrac{CA}{RP} = \dfrac{AB}{PQ}$
Hence $\rm CA = \dfrac{AB}{PQ} \times RP = \dfrac{(3\,m)}{(0.75\,m)} \times (1\,m) = 4\,m$
Question T6
Suppose that the pole RP (in Figure 10) is 2 m long, its shadow is 1 m long and the shadow of the tree is 3 m long. How tall is the tree?
Answer T6
The height of the tree is $\rm \left(\dfrac31 \times 2\right)\,m = 6\,m$.
Question T7
A vertical tree is growing on a hill that slopes upwards away from the sun at an inclination of 10° to the horizontal. The shadow of a pole 2 m long (held vertically on the hill) at the time of measurement is 1.5 m long and the shadow of the tree is 4.5 m long. Draw a diagram representing the situation and show that the properties of similar triangles still apply. What is the height of the tree?
(Assume that the tops of the shadows from the pole and the tree fall in the same place.)
Answer T7
In Figure 24, the tree is represented by AB, its shadow by BE, the pole by CD and its shadow by DE. Triangles ABE and CDE are similar (because AB and CD are both vertical and therefore parallel) and
$\rm \dfrac{AB}{CD} = \dfrac{BE}{DE}$
so that the height of the tree is given by
$\rm AB = CD \times \dfrac{BE}{DE} = \left(2 \times \dfrac{4.5}{1.5}\right)\,m = 6\,m$.
Sometimes it is not obvious when two triangles are similar. In Figure 12 ABC is a right–angled triangle with the right angle at B. We have drawn BD perpendicular to AC, and labelled the angles at A and C as α and β, so α + β = 90°.
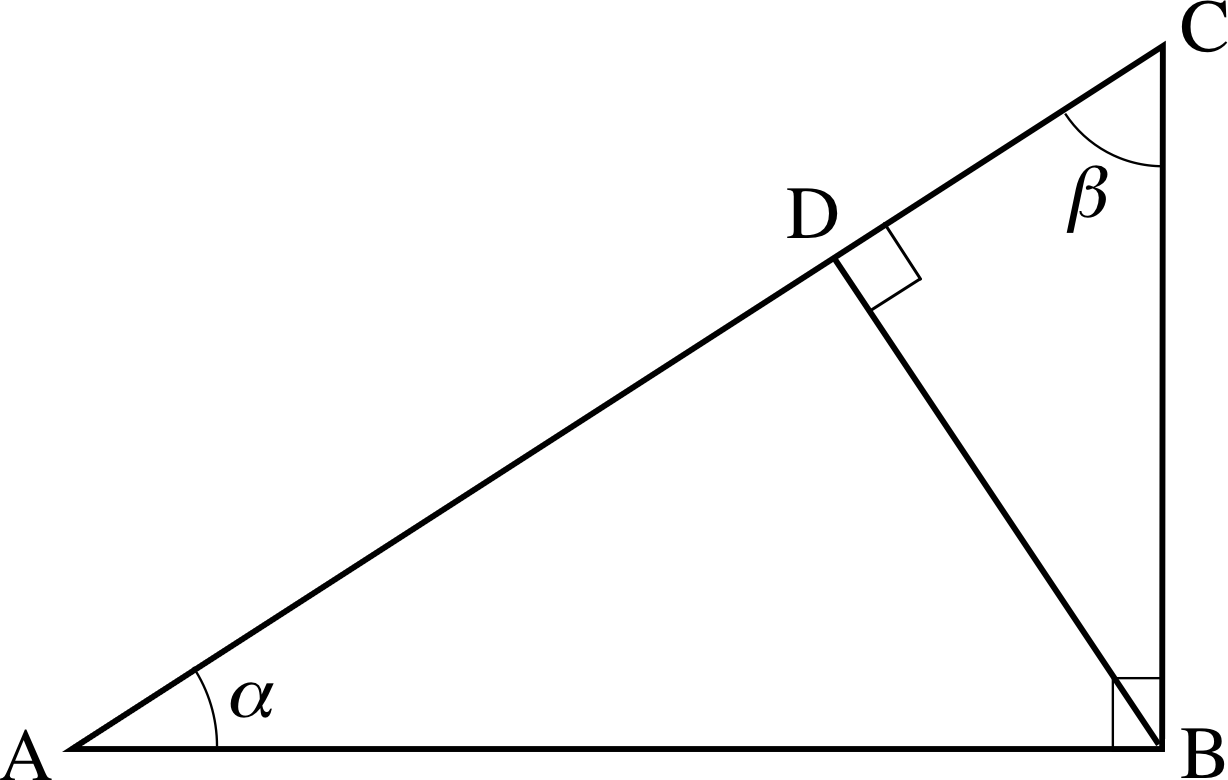
Figure 12 Similar triangles within a triangle.
✦ Can you see any similar triangles in Figure 12?
✧ In fact there are three. Look first at triangle ABD. One angle (AD^B) is a right angle; one (DA^B) is α. So the third angle, AB^D, must be (180° − 90° − α), and hence must be equal to β. Triangle ABD is therefore similar to triangle ABC, since it has the same three interior angles. To emphasize which sides are in the same ratio we can be more precise in the order in which we write the letters representing corresponding vertices, and say that the triangles ADB and ABC of Figure 12 are similar. This means that
$\dfrac{AD}{AB} = \dfrac{DB}{BC} = \dfrac{AB}{AC}$
4 Circles
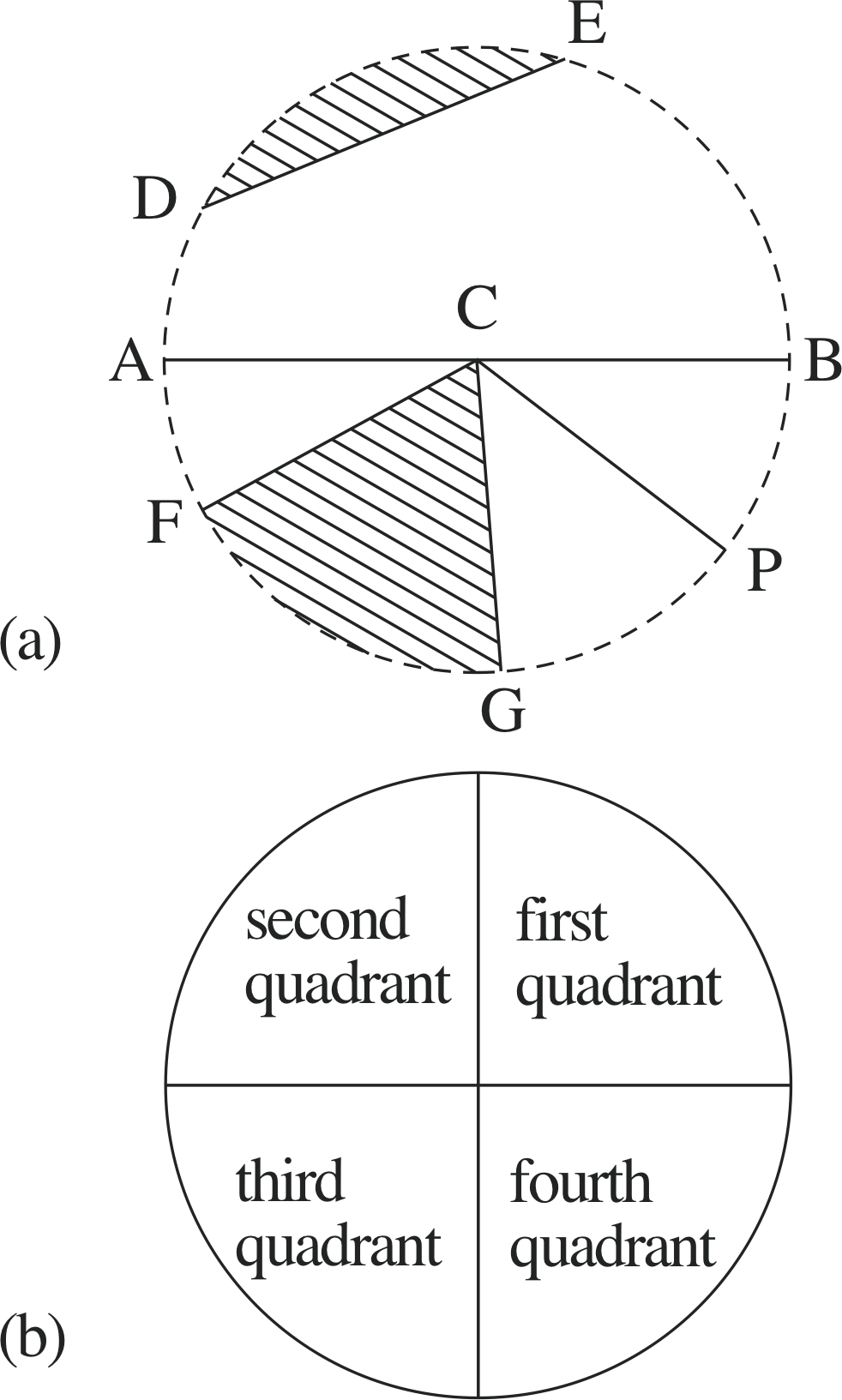
Figure 13 Features of a circle.
4.1 Parts of a circle
Various terms are used to describe the geometry of circles, and it is necessary to commit them to memory since they occur frequently.
A circle is the set of points in a plane which are the same distance (i.e. equidistant) from a given point (in the same plane) called the centre of the circle and the distance is called the radius of the circle. The set of points with a given property is sometimes called the locus, so that in this case we might say that a circle is the locus of all points equidistant from a given point (i.e. the centre). i The perimeter of the circle is known as the circumference of the circle. A straight line segment which passes through the centre of the circle and divides the interior of the circle into two equal parts is called a diameter (which is equal in length to twice the radius).
In Figure 13a C is the centre of the circle, ACB is a diameter and CP is a radius. The circumference of a circle plus its interior are sometimes known as a disc. The two halves of the circumference of the circle on either side of a diameter are called semicircles; two diameters which intersect at right angles (at the centre of the circle) divide the disc into four quadrants and when the two diameters are vertical and horizontal, as in Figure 13b the quadrants are labelled as shown.
A portion of the circumference of the circle between two points, such as D and E in Figure 13a, is called an arc of the circle. When DE is not a diameter, the longer route along the circumference from D to E is called a major arc and the shorter route is called a minor arc. The straight line segment DE which connects two points on the circumference is called a chord. When the chord is not a diameter, it divides the disc into two unequal regions, called segments. The smaller region (the shaded portion from D to E) is called a minor segment, the larger region is called a major segment.
The region inside a disc cut off by two radii, such as the shaded region FCG in Figure 13a, is called a sector, as is the remainder of the disc when this shaded region is removed. The minor arc FG of the circle is said to subtend an acute angle FC^G at the centre of the circle, whereas the major arc FG of the circle subtends an obtuse or reflex angle FC^G at the centre.
Two or more circles with the same centre but different radii are said to be concentric (see Figure 14b below) and the region bounded by two concentric circles is called an annulus.
✦ What term is used for a segment formed by an arc of a circle that subtends a right angle at the centre of a circle?
✧ This minor segment of the circle is known as a quadrant.
4.2 Properties of circles
The ratio of the circumference of a circle to its diameter is the well–known constant π (π is the Greek letter pi), which has an approximate value of 3.141 59 (though the less precise fractional value of 22/7 is often used).
So we can write c = πd
where c and d are the circumference and diameter of the circle, respectively.
The circumference of a circle of radius r is 2πr(2)
since the diameter is twice the radius.
So far in this module we have measured angles in degrees, a method which goes back to ancient times. In spite of its age, and its common use, this is not in fact a ‘natural’ system of measurement since there is nothing natural about choosing 360 rather than some other number. i
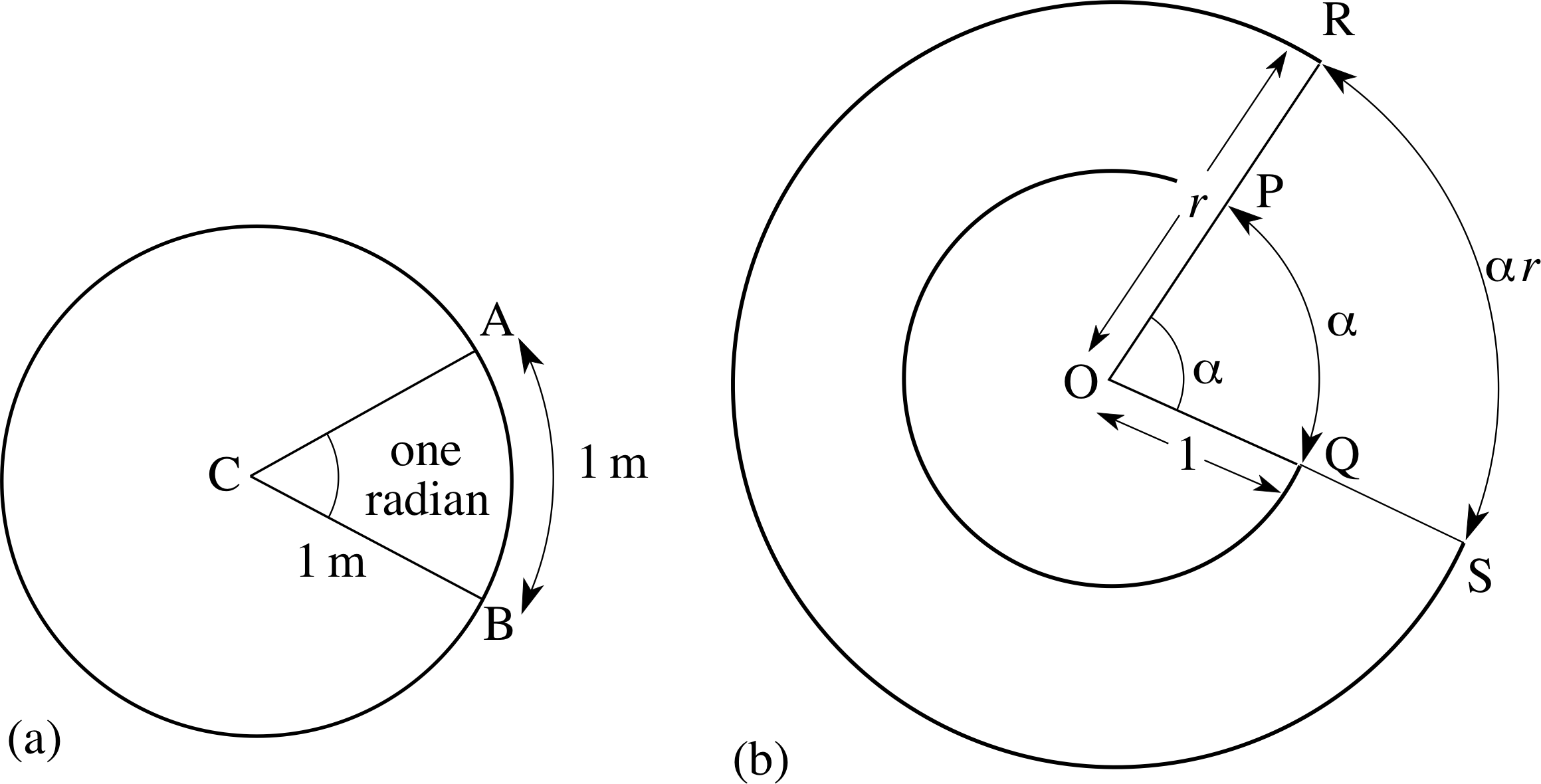
Figure 14 The radian measure.
An alternative scale, based on the lengths of arcs formed on a circle of unit radius (i.e. a unit circle), turns out to be far more appropriate in many circumstances (in particular in the context of calculus). Figure 14a represents a circle of radius 1 m, and the arc AB has been chosen so that it is exactly 1 m in length. The angle subtended by the arc at C is defined to be one radian. Since angles are preserved by scaling, there is nothing special about the choice of metres as our units of length, and in fact it is more usual to define a radian in terms of a circle of unit radius, without specifying what that unit of length might be.
In Figure 14b we have not specified the units of length, we have simply referred to them as ‘units’. Thus in Figure 14b the circle is of radius 1 unit. An arc, PQ say in Figure 14b, of length α units subtends an angle α radians at the centre O of the circle, as does an arc RS of length αr units on a circle of radius r.
Thus we have RS = αr so that α = RS/r, and since both RS and r have dimensions of length, it follows that angles measured in radians are dimensionless quantities. You should remember that:
An arc of a circle of radius r, subtending an angle α (in radians) at the centre of the circle, has length αr so that, in Figure 14b,
RS = αr(3)
If we extend the arc in Figure 14b so that RS is actually the circumference of the circle (and R coincides with S) we saw, in Equation 2, that its length will be 2πr. Therefore RS = αr = 2πr and α for this ‘arc’ is a full turn, i.e. 360°.
Therefore a complete turn of 360° corresponds to 2π radians, which we write as
360 degrees = 2π radians
From this we can deduce other relationships, for example,
180° = π radians, 90° = (π/2) radians, 60° = (π/3) radians, 45° = (π/4) radians, 30° = (π/6) radians.
1 radian is equivalent to (180/π)° which is approximately 57.3°.
✦ Express 3π/2 radians in degrees and 135° in radians.
✧ 2π radians = 360°, therefore 1 radian = $\dfrac{360°}{2\pi\,{\rm radians}}$, i
thus $\dfrac{3\pi}{2}\,{\rm radians} = \dfrac{360°}{2\pi} \times \dfrac{3\pi}{2} = 270°$
360°= 2π radians, therefore 1° = $\dfrac{2\pi\,{\rm radians}}{360°}$, thus 135° = $\dfrac{2\pi\,{\rm radians}}{360°} \times \dfrac{135°}{1} = \dfrac34\pi\,{\rm radians}$
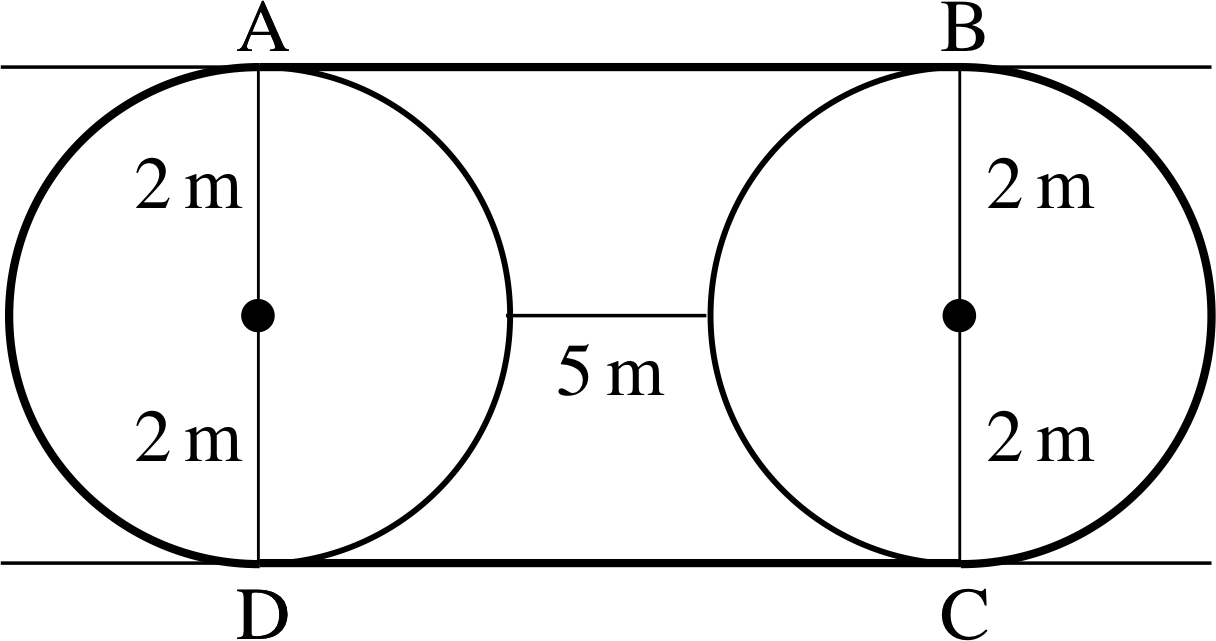
Figure 15 See Question T8.
Question T8
In Figure 15 a belt ABCDA passes round two pulleys as shown. Find the length of the belt.
Answer T8
The line from A to D is a diameter of the circle on the left in Figure 15. The portion of the belt which touches the pulley on the left is therefore half of the circumference.
The same is true for that part of the belt which touches the pulley on the right. The length from A to B is a radius + 5 m + a radius. The same is true for DC. The total length of the belt is therefore
$\rm \left[2 \times 2 \times \dfrac{2\pi}{2} + 2 \times (2 + 5 + 2)\right]\,m = [2\pi \times 2 + 2 \times 9]\,m = (4\pi + 18)\,m \approx 30.6\,m$
4.3 Tangents
In Figure 16 the line TP intersects the circle at just one point. Such a line is called a tangent to the circle and T is the point of contact where the tangent touches the circle. The tangent is perpendicular to the radius at T. The radius OT joins the point of contact to the centre of the circle. In Figure 15 the line AB is a tangent to both circles, in which case we say that it is a common tangent.
From any point outside the circle, say P in Figure 16, it is possible to draw two tangents to the circle PT and PS, and the lengths of PT and PS are equal.
✦ Show that the lengths of PT and PS are equal.
✧ OT = OS (since both are the radii of the circle)
OT^P = OS^P = 90° (the angle between radius and tangent) and OP (the hypotenuse) is common to both triangles. The triangles are therefore congruent by case (d) in our test for congruence in Subsection 3.1. It follows, therefore, that the lengths PT and PS are equal.
5 Areas and volumes
5.1 Areas of standard shapes
The areas of quadrilaterals and triangles
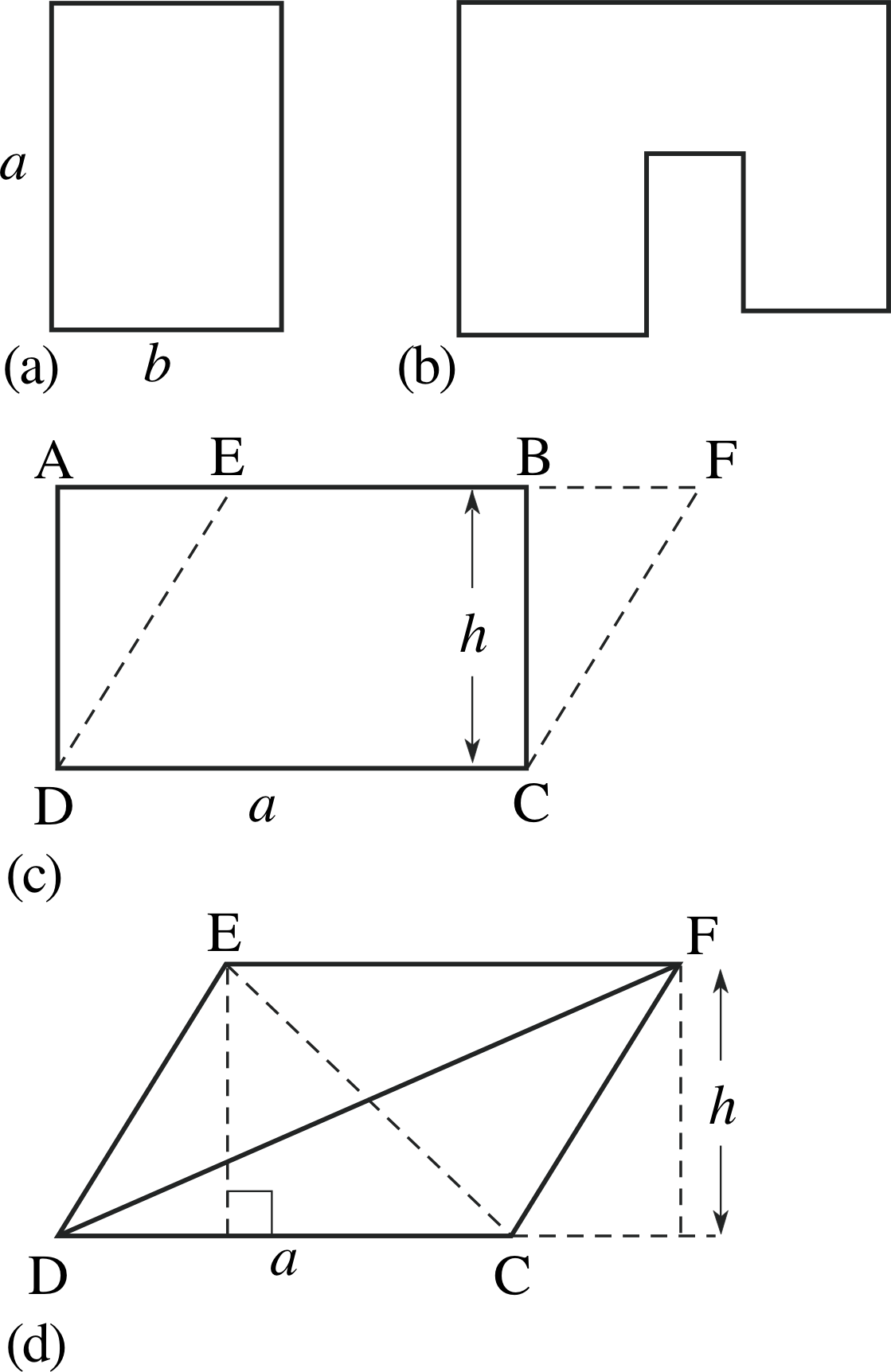
Figure 17 Rectangles, parallelograms and triangles.
The problem of finding areas of plane shapes is a common one. The area of the rectangle shown in Figure 17a is the product ab of the lengths of two adjacent (i.e. neighbouring) sides. Provided that we are given the sizes, it is easy to calculate the area of a shape such as that shown in Figure 17b by dividing it into suitable rectangles.
Figure 17c shows a rectangle ABCD with area ah. The triangles AED and BFC are congruent and so of equal area, and thus the area of the parallelogram EFCD is also ah. i With DC as the base of the parallelogram, the length h is known as the perpendicular height, so that:
The area of a parallelogram = base × perpendicular height
Figure 17d shows the same parallelogram as in Figure 17c, and the diagonal of the parallelogram EC divides the parallelogram into two parts of equal area (as does the diagonal DF). It follows that
area of triangle EDC = area of triangle DFC = ah/2 i
and in general i:
The area of a triangle = ½ base × perpendicular height
Another result that is sometimes of use relates the area of a triangle to the lengths of its sides. We quote this result without proof
The area of a triangle = $\sqrt{s(s-a)(s-b)(s-c)\os}$ where s = ½ (a + b + c)
A trapezium may be regarded as the sum of a parallelogram and a triangle. It follows that its area is given by
The area of a trapezium = ½ sum of parallel side lengths × perpendicular height

Figure 13 Features of a circle.
Area enclosed by a circle
We state without proof that the area enclosed by a circle of radius r is πr2.
This area is commonly (loosely) referred to as ‘the area of the circle’, though strictly we should say ‘the area enclosed by the circle’ or ‘the area of the disc’.
The area of a circle of (radius r) = πr2(4)
Area of a sector
Consider the shaded sector FCG shown in Figure 13a and suppose that the radius of the circle is r and that FC^G = θ (radians). The ratio of the area of the sector to the area of the circle is the same as the ratio of the angle θ to the angle of a complete turn, i.e. 2π.
In other words,
$\dfrac{\text{area of sector}}{\pi r^2} = \dfrac{\theta}{2\pi}$ (Remember that θ must be measured in radians.)
Hence:
The area of sector = ½ θr2(5)
Area of a segment
We can find the area of a segment by finding the area of a sector and then subtracting the area of a triangle. i
Question T9
In Figure 13a suppose that a minor arc DE is of length 2π metres and that the radius of the circle is 4 metres. i
(a) Find the angle θ subtended by the arc DE at C in both degrees and radians.
(b) Find the area of the triangle DEC.
(c) Find the area of the sector DEC.
(d) Find the area of the (larger) segment DAFGPBE.
(e) Find the area of the segment from D to E (the hatched area in Figure 13a).
Leave your answers in terms of π where appropriate.
Answer T9
(a) $\theta = \dfrac{{\rm arc DE}}{r} = \dfrac{\pi}{2} = 90°$
(b) If we take DC as the base of triangle DEC, the perpendicular height is EC, and it follows that the area of the triangle is ½ × (4 m) × (4 m) = 8 m2.
(c) Since DEC is a quadrant its area is ¼ πr2 = ¼ π (4 m)2 = 4π m2.
(d) The area of the circle is 16π m2 so that the required area is 16π − (4π − 8) = (12π − 8) m2.
(e) The area of the segment = area of sector DEC − area of triangle DEC which is (4π − 8) m2 ≈ 4.566 m2.
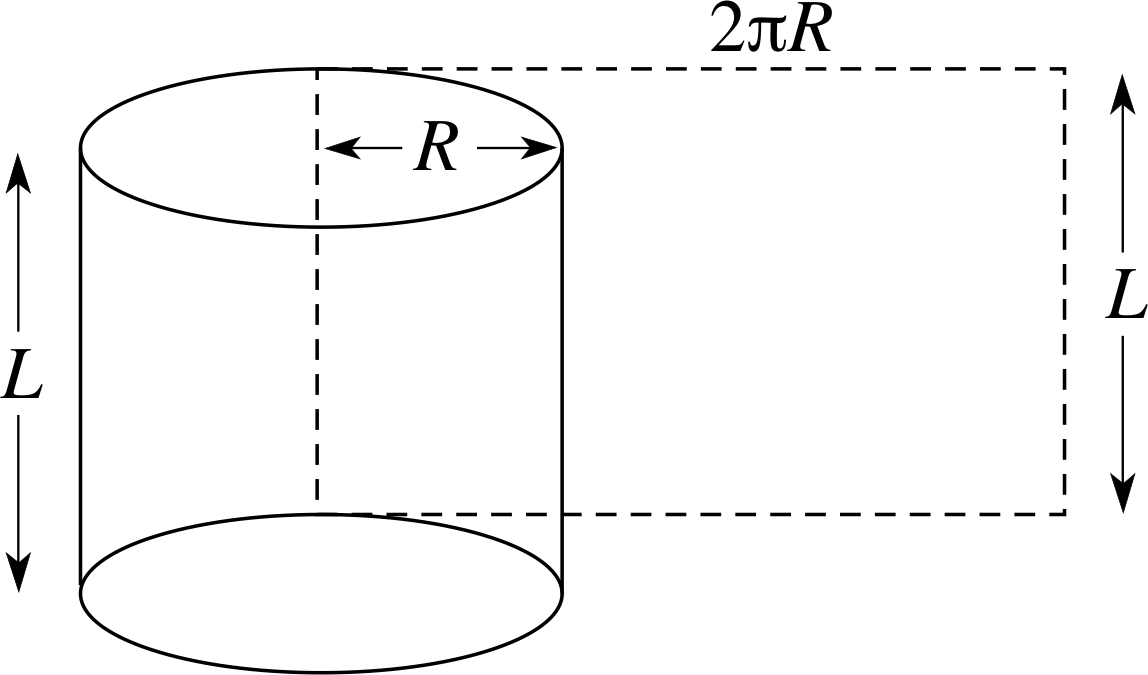
Figure 18 Surface area of a cylinder.
Area of the surface of a cylinder
The ends of a cylinder are circles. The curved surface of a cylinder can be opened out to form a rectangle as shown in Figure 18 so its area is the height of the cylinder times its circumference: that is, 2πR × L.
5.2 Volumes of standard solids
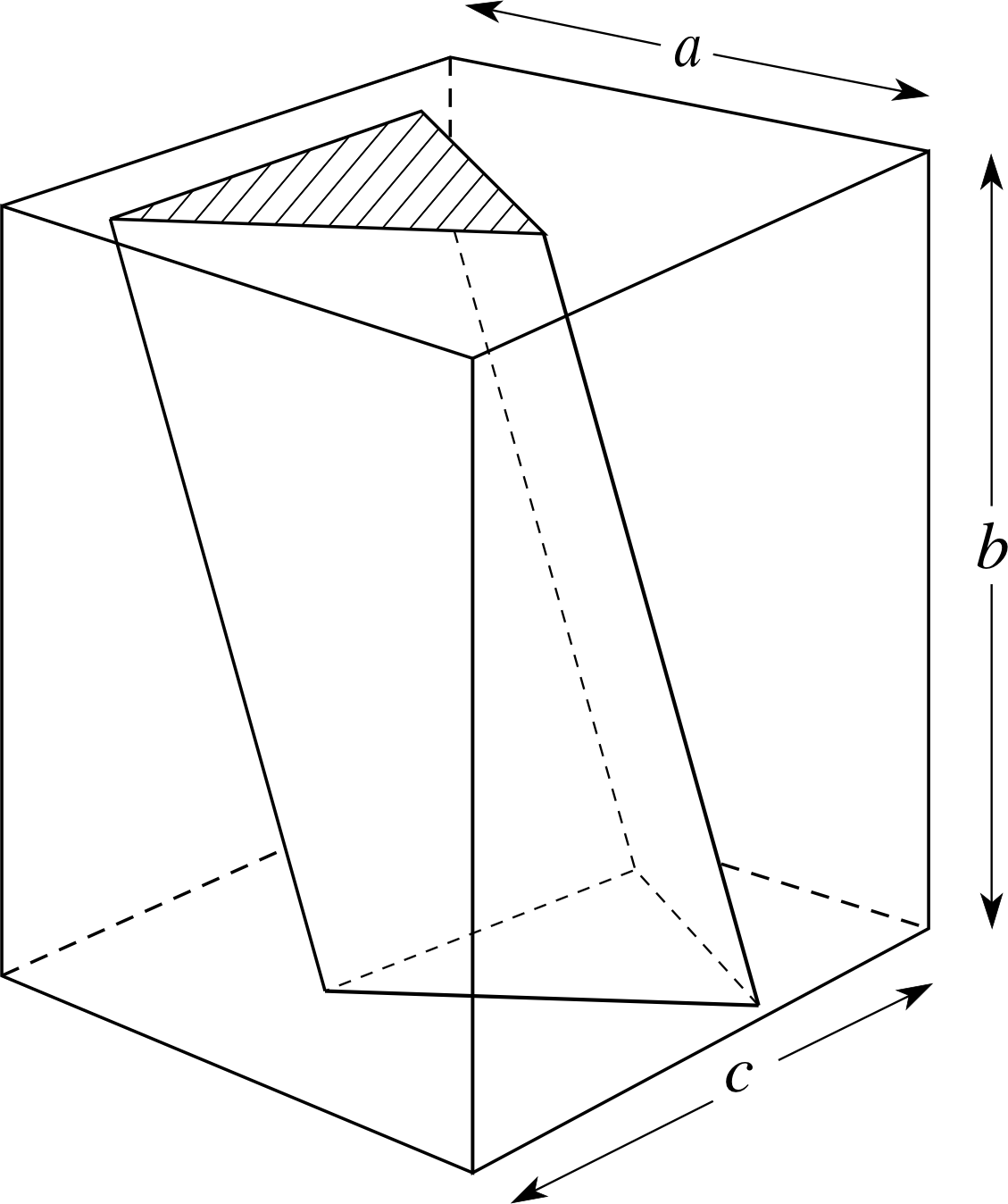
Figure 19 A cuboid and a prism.
Prisms
Just as it is useful to be able to find the area of geometrical shapes, so it is useful to know the volume of various solid shapes. One of the simplest solid shapes is a box, known more formally as a cuboid or a rectangular block.
If the sides of the cuboid are of length a, b and c, its volume is a × b × c.
In fact, a cuboid is a special case of a class of solids called prisms. A triangular prism is a solid for which the cross sections cut parallel to a certain direction are congruent triangles (oriented the same way), as shown by the hatched area in Figure 19. Every slice through the prism parallel to the base will produce a triangle identical to the shaded triangle. A cuboid is a prism for which the cross sections parallel to the base are identical quadrilaterals, and a cylinder is a prism for which the cross sections perpendicular to its axis are identical circles (see Figure 18). The perpendicular height of the prism is the length labelled b in Figure 19, and the hatched triangle is known as the cross–sectional area of the prism.
These terms can be easily generalized to prisms of any cross–sectional shape, and in general:
The volume of a prism = cross–sectional area × perpendicular height
✦ Find the volume of a cylinder with perpendicular height 1.5 m and whose cross section is a circle of radius 10 cm.
✧ The cross–sectional area is πr2 = π (0.1 m)2 = 0.01π m2, and the volume is therefore (0.01π m2 ) × (1.5 m) = 0.015π m3.
Question T10
A prism i has perpendicular height 5 m and its cross section is an annulus formed by circles of radius 1 m and 2 m. What is the volume of the prism?
Answer T10
The cross–sectional area is the area of the annulus between the circles of radius 1 m and 2 m. The area of the larger circle is π (2 m)2 = 4π m2 while the area of the smaller circle is π (1 m)2 = π m2, thus the area of the annulus is 3π m2. The volume of the prism is therefore 5 × 3π m2 = 15π m2.
Spheres
A sphere is a three–dimensional surface whose points are at an equal distance (the radius) from a fixed point (the centre of the sphere). Calculus i provides the easiest way of finding the area and volume of a sphere, and we will simply quote the results:
The surface area of a sphere of radius r is 4πr2 and its volume is $\frac43\pi r^3$(6)
✦ The surface area of a sphere is 10 m2. What is its volume?
✧ We have 4πr2 = 10 m2 and therefore
$r = \rm \sqrt{\dfrac{10\os}{4\pi}}\,m \approx 0.892\,m$. Hence the volume is $\rm \frac43\pi r^3 \approx 2.974\,m^3$.
Question T11
A given sphere has twice the volume of another. What is the ratio of their surface areas?
Answer T11
Let the radius of the smaller sphere be R and that of the larger sphere be S.
Then $\dfrac43\pi S^3 = 2 \times \dfrac43\pi R^3$
therefore S3 = 2R3
and it follows that S = (2R3)1/3 = 21/3R
The ratio of surface areas is
$\dfrac{4\pi S^2}{4\pi R^2} = \dfrac{S^2}{R^2} = (2^{1/3})^2 = 2^{2/3}\text{ or }4^{1/3} \approx 1.587$
6 Closing items
6.1 Module summary
- 1
-
Much of this module is devoted to the various terms that are used to describe Subsection 1.1geometric figures. When a line intersects a pair of Subsection 2.2parallel lines various angles between the lines are equal, in particular corresponding and alternate angles.
- 2
-
The sum of the interior angles of a polygon with n sides is (2n − 4) right angles.
- 3
-
Subsection 3.2Similar figures (in particular triangles) are the same shape, and corresponding lengths in two similar figures are in the same ratio.
- 4
-
Subsection 3.1Congruent figures are the same shape and the same size. The four minimal specifications of a unique triangle are as follows:
(a) State the length of all three sides. (SSS)
(b) State the lengths of two sides and the angle between them. (SAS)
(c) State the length of one side and the angles at each end of it. (ASA)
(d) Specify a right angle, the length of the hypotenuse and the length of one other side. (RHS) If any of these specifications is common to two triangles, then those triangles must be congruent.
- 5
-
The sides a, b and c of a right–angled triangle are related by Pythagoras’s theorem
c2 = a2 + b2(Eqn 1)
where c is the hypotenuse of the triangle.
- 6
-
The Subsection 4.2circumference of a circle of radius r is 2πr.
- 7
-
One radian is the angle subtended at the centre of a unit circle by an arc of unit length. The length of an arc of a circle of radius r which subtends an angle θ (in radians) at the centre is rθ.
360 degrees = 2π radians
- 8
-
A Subsection 4.3tangent is a line that meets a circle at one point. A right angle is formed by the tangent and a radius drawn to the point of contact.
- 9
-
The area of a parallelogram is the base times the perpendicular height, and the area of a triangle = ½ base × perpendicular height.
- 10
-
The area of a Section 4circle of radius r is πr2 and the area of a sector subtending an angle θ at the centre is ½ θr2.
- 11
-
The volume of a prism is the cross-sectional area times the perpendicular height.
- 12
-
The surface area of a sphere of radius r is 4πr2 and its volume is $\frac43\pi r^3$.
6.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Identify the different types of angles formed when lines intersect and calculate their values.
- A3
-
Identify which angles formed by a line intersecting two parallel lines are equal.
- A4
-
Classify the different types of quadrilateral.
- A5
-
Understand and apply the simple properties of polygons.
- A6
-
Classify the different types of triangle and apply the test for the congruence of two triangles using the four minimal specifications of a triangle.
- A7
-
Recognize when two triangles are similar and compare the lengths of corresponding sides.
- A8
-
Recognize the main features of a circle, including tangents, arcs, segments and sectors.
- A9
-
Evaluate areas and volumes of standard shapes.
- A10
-
Apply Pythagoras’s theorem and use it to identify right–angled triangles.
Study comment You may now wish to take the folowing Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
6.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions each of which tests one or more of the Achievements.
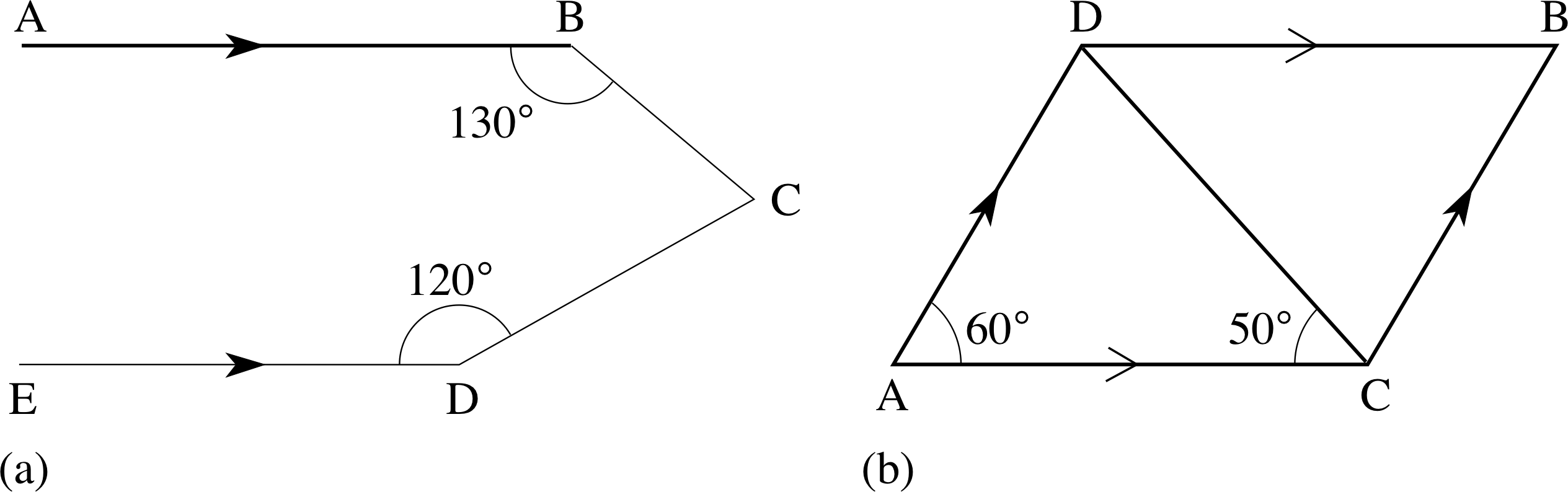
Figure 20 See Question E1.
Question E1 (A2 and A3)
Find the angle BC^D in Figures 20a and 20b.
Answer E1
(a) In Figure 20a draw a line FCG parallel to AB and ED through C. Then:
BC^G = AB^C = 130° (alternate angles)
DC^G = ED^C = 120° (alternate angles)
BC^D = 360° − 130° − 120° = 110°
(b) AD^C = 180° − 60° − 50° = 70°
BC^D = AD^C = 70° (alternate angles).
(Reread Subsection 2.2 if you had difficulty with this question.)

Figure 9 (b) See Question E2.
Question E2 (A3 and A5)
Suppose that you are told that in Figure 9b AC^B = 90° and that AM = MC. Prove that M is the mid–point of AB.
Answer E2
Triangle AMC is isosceles since MA = MC and it follows that MA^C = MC^A. Now MC^A + MC^B = 90°, hence MA^C + MC^B = 90°. But MA^C + MB^C = 90°. (Because MA^C + MB^C + AC^B =180°.) Therefore MC^B = MB^C. Triangle MCB is therefore isosceles, from which it follows that MC = MB. Hence MA = MB.
(Reread Subsection 2.3 if you had difficulty with this question.)
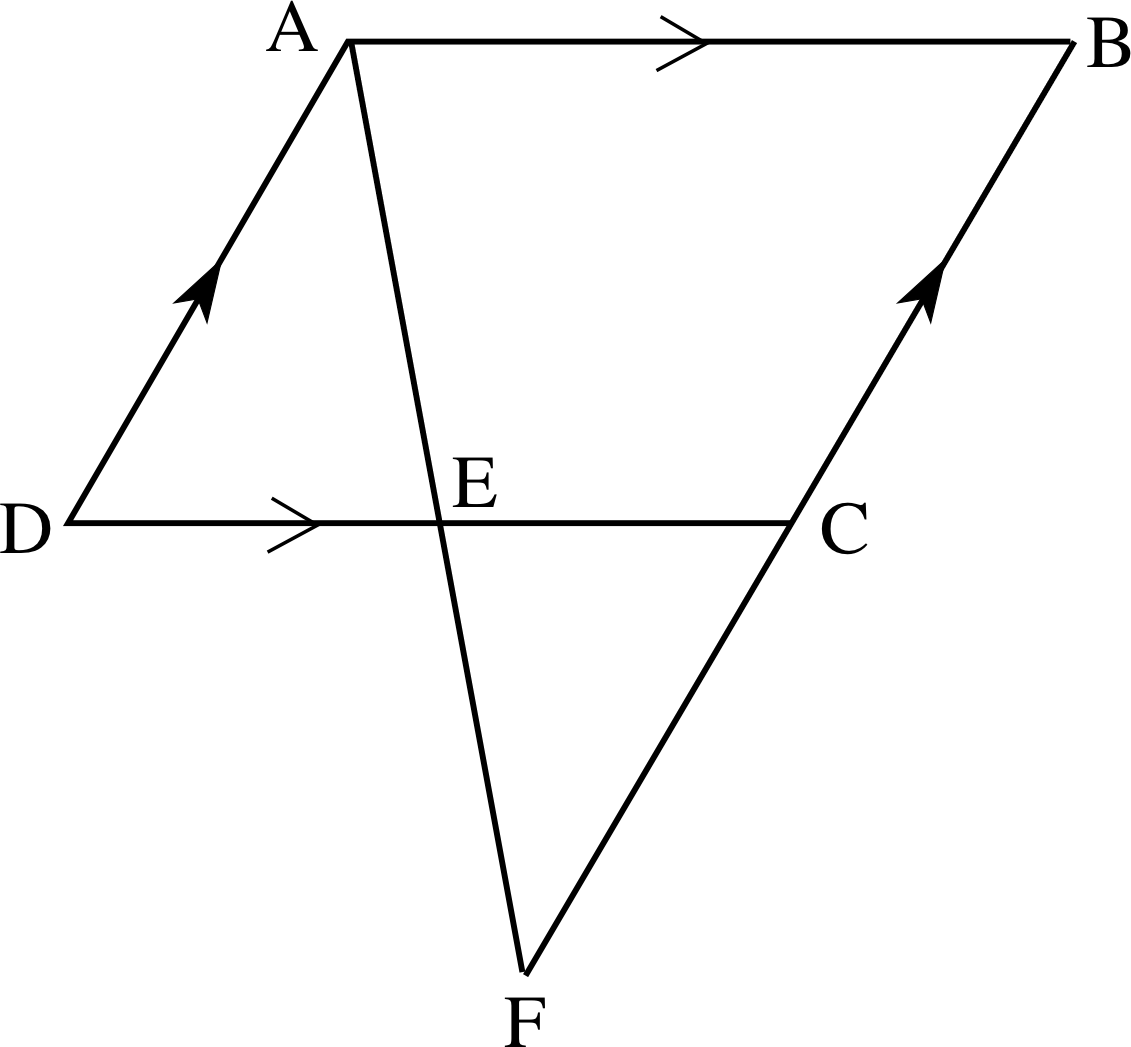
Figure 21 See Question E3.
Question E3 (A3 and A7)
In Figure 21 ABCD is a parallelogram. A line through A meets DC at E and meets BC produced at F. Show that triangles ADE and FCE are similar. If DE = 15 mm, EC = 10 mm and FC = 5 mm find AD.
Answer E3
AE^D = CE^F (vertically opposite angles).
DA^E = EF^C (alternate angles)
Hence AD^E = EC^F (angle sum is 180°, or alternate angles) and so the triangles are similar. Then:
$\rm \dfrac{AD}{FC} = \dfrac{AE}{FE} = \dfrac{DE}{CE}$, so $\rm AD = \left(5 \times \dfrac{15}{10}\right)\,mm = 7.5\,mm$.
(Reread Subsection 5.1 if you had difficulty with this question.)
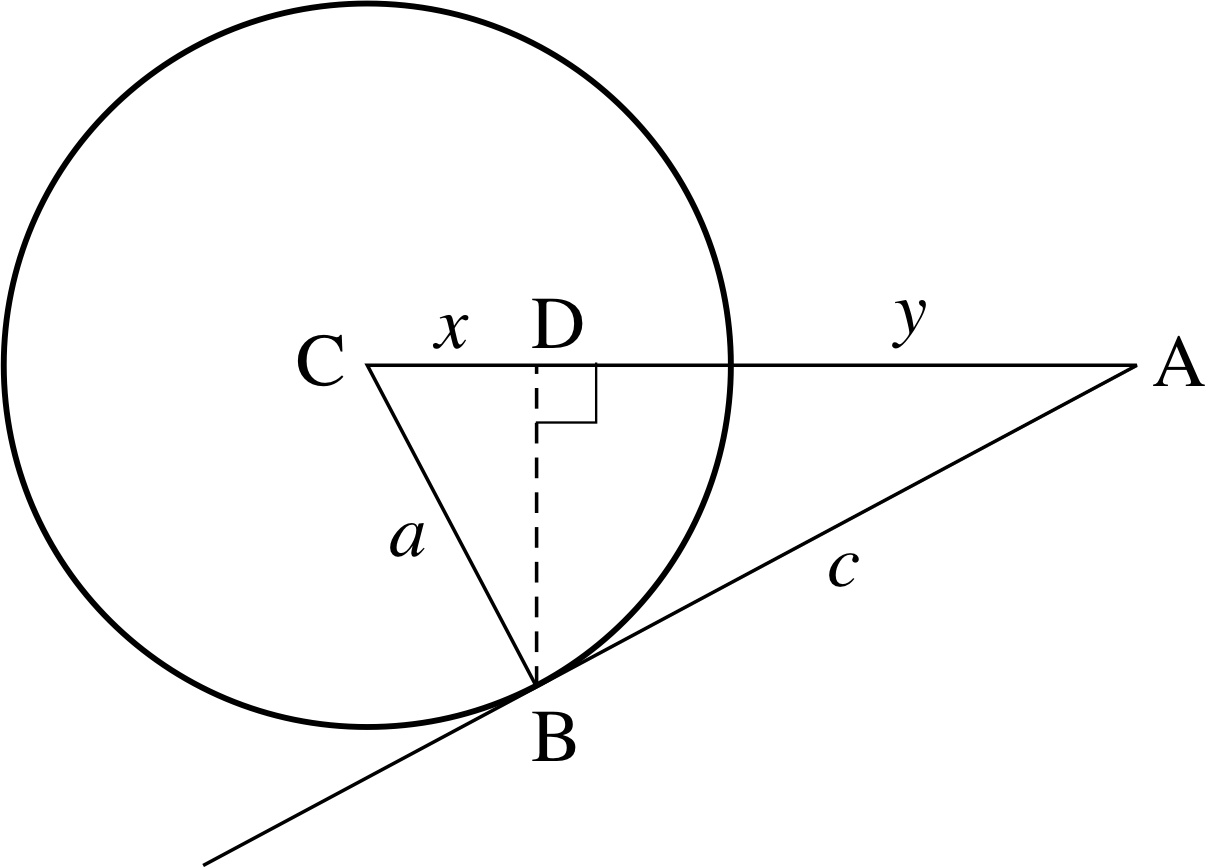
Figure 22 See Question E4.
Question E4 (A7, A8 and A10)
In Figure 22 AB is a tangent to the circle of radius a and centre C. DB represents the perpendicular height of the triangle ABC with AC as its base. The lengths CD and DA are x and y, respectively.
Use an argument based on similar triangles to show that:
$\dfrac xa = \dfrac{a}{x+y}\quad\text{and}\quad\dfrac yc = \dfrac{c}{x+y}$ and (AC)2 = a2 + c2.
Answer E4
The angle CB^A is a right angle (because AB is a tangent) and therefore the triangles CDB, CBA and BDA are similar. It follows that:
$\rm \dfrac{CD}{CB} = \dfrac{CB}{CA}$ or $\dfrac{x}{a} = \dfrac{a}{x+y}$
Also $\rm \dfrac{DA}{BA} = \dfrac{BA}{CA}$ or $\dfrac{y}{c} = \dfrac{c}{x+y}$
Therefore
$x+y = \dfrac{a^2}{x+y} + \dfrac{c^2}{x+y}$, so that $(x+y)^2 = a^2+c^2$
which gives the required result. (The result can also be obtained directly from Pythagoras’s theorem.)
(Reread Subsection 3.2 if you had difficulty with this question.)
Question E5 (A9)
A washer is in the form of a cuboid with sides of length 1.5 cm and thickness 4 mm with a circular hole of radius 0.6 cm drilled through its centre. Calculate the volume of the washer.
Answer E5
Area of the square is (1.5 cm) × (1.5 cm) = 2.25 cm2
the area of the circle = π (0.6 cm)2 = 0.36π cm2
the cross–sectional area of the washer is (2.25 − 0.36π) cm2 ≈ 1.119 cm2
therefore the volume of the washer is ≈ (1.119 cm2) × (0.4 cm) ≈ 0.448 cm3 = 0.448 × 10−6 m3
(Reread Section 5 if you had difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 6Closing items.