MATH 1.7: Series expansions and approximations |
PPLATO @ | |||||
PPLATO / FLAP (Flexible Learning Approach To Physics) |
||||||
|
1 Opening items
1.1 Module introduction
This module is concerned with representing functions and numerical constants by means of series. Examples of numerical series are
1 + 2 + 3 + 4 + ... + n
and$\pi = 4\left(1-\dfrac13+\dfrac15-\dfrac17+\dfrac19-\dots\right)$
where the ellipsis ‘...’ indicates that the series continues, following the same pattern. An example of a series which represents a function is
$\sin(x) = x - \dfrac{x^3}{1\times 2\times 3} + \dfrac{x^5}{1\times 2\times 3\times 4\times 5} + \dots$
Notice that in the last two examples, both series carry on indefinitely.
Many of the numerical constants that occur in mathematics (notably, π and e) can be written as series. Functions represented by series occur throughout mathematics and physics and such series are frequently used to obtain solutions to many types of equations and (though not in this module) to evaluate integrals. Moreover, series are often used to approximate well–known functions. In fact, every time you use a computer or your calculator to evaluate something like sin(x) or loge(x) you are probably using a series approximation.
The discussion of series contained in this module is divided into two parts; Section 2 deals with finite series and Section 3 with infinite series. Within Section 2 are the basic definitions of sequence and series along with the symbols and terminology that will be used elsewhere in the module. Section 2 also contains a survey of various standard series, including arithmetic and geometric progressions and the binomial expansion. Subsection 2.6 also contains an introduction to the method of induction that can be used to prove various results relating to series and their sums. Section 3 presents the series that represent various elementary functions (sin(x), cos(x), etc.), considers the conditions under which the sum of terms in an infinite series can lead to a finite result and discusses the many applications of the truncated series that provide approximations to the functions represented by the full series.
Study comment Having read the introduction you may feel that you are already familiar with the material covered by this module and that you do not need to study it. If so, try the following Fast track questions. If not, proceed directly to the Subsection 1.3Ready to study? Subsection.
1.2 Fast track questions
Study comment Can you answer the following Fast track questions? If you answer the questions successfully you need only glance through the module before looking at the Subsection 4.1Module summary and the Subsection 4.2Achievements. If you are sure that you can meet each of these achievements, try the Subsection 4.3Exit test. If you have difficulty with only one or two of the questions you should follow the guidance given in the answers and read the relevant parts of the module. However, if you have difficulty with more than two of the Exit questions you are strongly advised to study the whole module.
Question F1
Explain what is meant by n! and use the method of induction to show that
$\displaystyle \sum_{k=1}^{\infty} (k!)k = (n+1)! -1$
Answer F1
Factorial n, written n!, is defined by
n! = n (n − 1)(n − 2)(n − 3) ... 2 × 1 for n ≥ 1
together with 0! = 1
To prove the equation by induction, consider $\displaystyle \sum_{k=1}^{n+1} (k!)k$
which can be split into two terms
$\displaystyle \sum_{k=1}^{n+1} (k!)k = \sum_{k=1}^{n} (k!)k + (n+1)!(n+1)$
Using the result given in the question, the first term on the right–hand side is (n + 1)! − 1, so we find
$\begin{align}\sum_{k=1}^{n+1} (k!)k& = (n+1)! - 1 + (n+1)!(n+1)\\& = (n + 1)![1 + (n + 1)] − 1\\&= (n + 1)!(n + 2) − 1 = (n + 2)! − 1\end{align}$
But this is just the result given in the question with (n + 1) replacing n. So if the result is true for n, it is true for (n + 1). For n = 1 we have
$\displaystyle \sum_{k=1}^{n} (k!)k = \sum_{k=1}^{1} (k!)k = (1!)1 = 1$
and(n + 1)! − 1 = (1 + 1)! − 1 = 1
showing that the formula is valid for the lowest value of n. This completes the proof by induction.
Question F2
Write down the binomial expansion of (a + b) n and define the binomial coefficient nCr. Show that the binomial coefficient satisfies
1 + nC1 + nC2 + nC3 + ... + nCn = 2n
Answer F2
The binomial expansion is
$\begin{align}(a+b)^n & = ~^n\!C_na^n + ~^n\!C_{n-1}a^{n-1}b + \dots + ~^n\!C_{n-r}a^{n-r}b^r + \dots + ~^n\!C_1ab^{n-1} + ~^n\!C_0b^n\\ & = \sum_{k=0}^{n} ~^n\!C_{n-k}a^{n-k}b^k\end{align}$
The binomial coefficient $\!^n\!C_r$ is defined by
$\!^n\!C_r = \dfrac{n(n−1)(n−2)\dots(n−r+2)(n−r+1)}{r(r − 1)(r − 2) \dots 2 \times 1}$
where n ≥ r, which can also be written as
$\!^n\!C_r = \dfrac{n!}{r!(n-r)!}$
Putting a = b = 1 in the binomial expansion, we find
$(1+1)^n = ~^n\!C_n + ~^n\!C_{n-1} + \dots + ~^n\!C_{n-r} + \dots + ~^n\!C_1 + ~^n\!C_0$
and since $\!^n\!C_0 = 1$ we obtain the required result
$1+~^n\!C_1+~^n\!C_2+\dots+~^n\!C_n = 2^n$
Question F3
(a) Write down the series for sin(x) and cos(x) in powers of x.
(b) Using the first three terms of each of these series, obtain approximate values for cos(60°) and sin(30°).
Answer F3
(a) The series for sin(x) and cos(x) are
$\displaystyle \sin(x) = \sum_{n=0}^{\infty} \dfrac{(-1)^nx^{2n+1}}{(2n+1)!} = x -\dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \dots$ for all x
$\displaystyle \cos(x) = \sum_{n=0}^{\infty} \dfrac{(-1)^nx^{2n}}{(2n)!} = x -\dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \dots$ for all x
(b) When using a power series such as that given above for sin(x) to find an approximate value for sin(θ) where θ is a given angle, it is important to remember that x is a dimensionless variable whose numerical value is given by x = θ/rad. In other words, if θ is given in radians, x is equal to the numerical value of θ, but if θ is given in degrees then it is necessary to convert θ into radians before you can ‘drop the units’.
60° = (π/3) rad = 1.0472 rad, so 60°/rad = 1.0472
$\begin{align}\cos(1.0472) & \approx 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!}\\& \approx 1 - \dfrac{(1.0472)^2}{2} + \dfrac{(1.0472)^4}{24} \approx 0.50\,794\end{align}$
30° = (π/6) rad = 0.5236 rad, so 30°/rad = 0.5236
$\begin{align}\sin(0.5236) & \approx x-\dfrac{x^3}{3!} + \dfrac{x^5}{5!}\\& \approx 0.5236 - \dfrac{(0.5236)^3}{6} + \dfrac{(0.5236)^5}{120} \approx 0.5000\end{align}$
Question F4
Use an appropriate test to discover whether or not the following series converges:
$\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{2^nn}$
Answer F4
For convenience we write $a_n = \dfrac{1}{2^nn}$ and evaluate R, where
$\displaystyle R = \lim_{n\rightarrow\infty} \left(\dfrac{a_{n+1}}{a_n}\right) = \lim_{n\rightarrow\infty} \left[\dfrac{2^n(n)}{2{n+1}(n+1)}\right] = \lim_{n\rightarrow\infty} \left[\dfrac12\dfrac{n}{(n+1)}\right] = \dfrac12$
Therefore this series converges by d’Alembert’s ratio test, since R < 1. (It can be show that the sum of the series is actually loge(2).)
Question F5
Write (1 + x) r as a series in powers of x and use this series to calculate the positive square root 1.1 to four decimal places. Compare the result with the answer given by a calculator.
Answer F5
The series for (1 + x) r in powers of x is
$(1+x)^r = 1 + \dfrac{rx}{1!} + \dfrac{r(r-1)x^2}{2!} + \dfrac{r(r-1)(r-2)x^3}{3!} + \dots$ for −1 < x < 1
so we have
$(1+x)^{1/2} = 1 + \left(\dfrac12\right)\dfrac{x}{1!} + \left(\dfrac12\right)\left(\dfrac{-1}{2}\right)\dfrac{x^2}{2!} + \left(\dfrac12\right)\left(\dfrac{-1}{2}\right)\left(\dfrac{-3}{2}\right)\dfrac{x^3}{3!} + \left(\dfrac12\right)\left(\dfrac{-1}{2}\right)\left(\dfrac{-3}{2}\right)\left(\dfrac{-5}{2}\right)\dfrac{x^5}{5!} + \dots$
and putting x = 0.1 we have
$(1.1)^{1/2} = 1 + \dfrac{0.1}{2}- \dfrac{0.01}{8} + \dfrac{0.001}{16}- \dfrac{5\times 0.0001}{128} + \dots$
The fifth term is less than 0.0001 so we would expect the first four terms to give us a result to four decimal places; that is
$\sqrt{1.1\os} \approx 1.0488$
A calculator gives the result, 1.048 0809.
1.3 Ready to study?
Study comment To begin the study of this module you need to be familiar with the term mean and with the basic idea of a function, and, in particular, with the functions exp(x), sin(x) and cos(x). You should also be able to simplify, expand and evaluate basic algebraic expressions, solve simple equations and use inequalityinequality symbols (<, ≤, ≥, >) to indicate ranges of numerical values. If you are uncertain about any of these terms, you should consult the Glossary, which also indicates where to look in FLAP for more complete explanations. The following questions will help you to decide whether you need to review some of these topics before embarking on this module.
A special note about $\sqrt{x\os}$: Throughout this module we adopt the convention that $\sqrt{x\os}$ is the positive square root of x.
Question R1
In your own words, explain the meaning of −1 ≤ x < 1. If y = 1 − x, what can you say about the possible values of y over the given range of values of x?
Answer R1
−1 ≤ x < 1 means that x is greater than or equal to −1 but less than 1.
It is an example of the use of inequalities to specify a range of values. If y = 1 − x, then y decreases as x increases. Furthermore, when x = −1, y = 1 + 1 = 2, and when x = 1, y = 1 − 1 = 0. So due to the relationship between x and y and the restrictions on x we can say 0 < y ≤ 2.
Consult inequality and range in the Glossary for further information.
Question R2
Show that
$\dfrac{n(n+1)(2n+1)}{6} - 30 = \dfrac{(n-4)(2n^2 +11n+45)}{6}$
Answer R2
Introducing a common denominator of 6 we obtain
$\dfrac{n(n+1)(2n+1)}{6} - 30 = \dfrac{n(n+1)(2n+1)-180}{6}$
expanding the brackets in the last expression we find
$\dfrac{n(n+1)(2n+1)-180}{6} = \dfrac{2n^3+3n^2-180}{6}$
but$\dfrac{(n−4)(2n^2 +11n+45)}{6} = \dfrac{2n^3+3n^2+n−180}{6}$
So the two expressions are equivalent, as required.
Consult rearrangement and common denominator in the Glossary for further information.
2 Finite series
2.1 Sequences
In physics and mathematics we are often interested in a succession of numbers such as $\dfrac12, \dfrac23, \dfrac34, \dots$ and so on.
Such an ordered collection of numbers is known as a sequence. i
Sequences may also arise as the result of physical experiments (such as temperature measurements at hourly intervals) in which case they are likely to consist of physical quantities (i.e. combinations of numbers and units, such as 10°C, 8°C, 6°C, ...), or they may even consist of algebraic expressions such as x, x2, x3, ... . The essential point is that a sequence is not just a collection of terms, but that it is an ordered collection of terms. The principle that underlies the ordering may not always be as obvious as that in the examples we have quoted, but it is an essential part of the definition of a sequence. Because the terms of a sequence are ordered we can, if we wish, number them. For instance the sequence of temperatures could be denoted T1, T2, T3, .... The temperatures themselves might vary in a complicated way, but the position of each in the sequence is made clear by the subscript (that is, the small number written after the symbol). In general, a subscript may have a limited range of possible values (such as 1, 2, 3) or an infinite range (such as 1, 2, 3, ...).
The subscripts may not necessarily start at one (zero is very common) and the difference between successive subscripts is not always one. If, for example, we were only interested in the odd temperature readings, it might be sensible to label them T1, T3, T5 and so on. Subscripts provide a handy way of describing all the terms in a sequence together, since we can speak of ‘the sequence Ti where the subscript i runs from 1 to 24,’ or whatever. i
2.2 An introduction to series
One use of sequences is in describing the sum of sets of numbers. Suppose, for example, that we have 24 hourly temperature readings, which we call Ti, where i = 1, 2, 3, ..., 24, then the mean or average temperature, $\langle T\rangle$ i, is given by
$\langle T\rangle = \dfrac{1}{24}(T_1+T_2+T+3+T_4+ \dots + T_{24})$
Such a sum is called a finite series (or sometimes, more briefly, a series). It is clear that writing summations explicitly can be rather cumbersome and so it is convenient to introduce the symbol, ∑ (the Greek capital letter, sigma), to mean ‘sum all terms to the right’.
Using this summation symbol we can rewrite the expression for $\langle T\rangle$ as
$\displaystyle \langle T\rangle = \dfrac{1}{24}\sum_{i=1}^{24} T_i$ i
Notice that i, the quantity that increases by 1 as we go from one term to the next, is indicated below the ∑ symbol, along with its lowest value. This lowest value of i tells us the starting point or lower limit of the sum. The value of i that determines the final term, the upper limit, is put above the ∑ symbol. In the above example, i happens to be the subscript that distinguishes one term from the next, but as you will shortly see this is not always the case. More generally, the variable that appears below the summation is called the summation variable i and should be presumed to change in steps of 1 from the lower limit to the upper limit.
Some examples are given below: pay particular attention to (c), and note that the summation variable might start from a value other than 1 as in case (d), or it might be decreasing, as in (e):
(a) $\displaystyle \sum_{i=1}^5 i = 1 + 2 + 3 + 4 + 5 = 15$
(b) $\displaystyle \sum_{k=1}^3 (2k+1) = (2+1) + (4+1) + (6+1) = 3 + 5 + 7 = 15$
(c) $\displaystyle \sum_{i=1}^4 a = a + a + a + a = 4a$ i
(d) $\displaystyle \sum_{i=3}^k 2i = 6 + 8 + \dots + (2k-2) + 2k$
(e) $\displaystyle \sum_{i=14}^0 3i = (3\times 4)+ (3\times 3) + (3\times 2) + (3\times 1) + (3\times 0) = 30$
Question T1
Evaluate $\displaystyle \sum_{n=3}^7 n$
Answer T1
Writing out the summation explicitly, we have
$\displaystyle \sum_{n=3}^7 n = 3 + 4 + 5 + 6 + 7 = 25$
Question T2
Two important statistical quantities that are often used to analyse a collection of data, such as x1, x2, ..., xn, are the mean
$\displaystyle \langle x \rangle = \dfrac 1n\sum_{i=1}^n x_i$
and the standard deviation σn
$\displaystyle \sigma_n = \sqrt{\dfrac 1n\sum_{i=1}^n\left(x_i-\langle x \rangle\right)}$
Find $\langle x \rangle$ and σn for the data set x1 = 1.5, x2 = 2.0, x3 = 5.5.
Answer T2
The mean is given by
$\displaystyle \langle x \rangle = \dfrac 1n\sum_{i=1}^n = \dfrac13(1.5 + 2.0 + 5.5) = 3.0$
and the standard deviation is
$\displaystyle \sigma_n = \sqrt{\dfrac 1n\sum_{i=1}^n (x_i-\langle x \rangle)^2} = \sqrt{\dfrac13\left[(-1.5)^2+ (-1.0)^2+ (2.5)^2\right]} = \sqrt{\dfrac{9.5}{3}} = 1.78$
2.3 Properties of the summation symbol ∑
Suppose we have evaluated a finite series of the form
$\displaystyle \sum_{i=1}^N x_i = x_1 + x_2 + x_3 + \dots + x_N$(1)
and we now want to know the result of
$\displaystyle \sum_{i=1}^N 2x_i = 2x_1 + 2x_2 + 2x_3 + \dots + 2x_N$(2)
In fact, it is clear from the right–hand sides of these two equations that the sum in Equation 2 is just twice that in Equation 1, so we can say
$\displaystyle \sum_{i=1}^N 2x_i = 2 \sum_{i=1}^N x_i$
This is a particular example of a general rule for manipulating the ∑ symbol which, together with two other similar rules, is explained in this subsection. In each case the general rule may be derived by writing out the original sum explicitly, doing some (usually trivial) algebra and then expressing the result using the summation symbol again. Here are the three rules together with their derivations.
The constant multiple rule for summationconstant multiple rule $\displaystyle \sum_{i=1}^N ax_i = a \sum_{i=1}^N x_i$(3)
$\begin{align} \rm{\it{Derivation}}~~~~\sum_{i=1}^N ax_i & = ax_1 + ax_2 + ax_3 + \dots + ax_N\\& = a(x_1 + x_2 + x_3 + \dots + x_N)\\& = a \sum_{i=1}^N ax_i\end{align}$
This is the generalization of the result given above, since if we put a = 2 we find
$\displaystyle \sum_{i=1}^N 2x_i = 2 \sum_{i=1}^N x_i$
The constant addition rule for summationconstant addition rule $\displaystyle \sum_{i=1}^N (x_i+b) = Nb + \sum_{i=1}^N x_i$(4) i
$\begin{align} \rm{\it{Derivation}}~~~~\sum_{i=1}^N (x_i+b) & = (x_1+b) + (x_2+b) + (x_3+b) + \dots + (x_N+b)\\& = Nb+(x_1 + x_2 + x_3 + \dots + x_N)\\& = Nb + \sum_{i=1}^N x_i\end{align}$
The summation over addition rule $\displaystyle \sum_{i=1}^N (x_i+y_i) = \sum_{i=1}^N x_i + \sum_{i=1}^N y_i$(5) i
$\begin{align} \rm{\it{Derivation}}~~~~\sum_{i=1}^N (x_i+y_i) & = (x_1+y_1) + (x_2+y_2) + (x_3+y_3) + \dots + (x_N+y_N)\\& = (x_1 + x_2 + x_3 + \dots + x_N)+(y_1 + y_2 + y_3 + \dots + y_N)\\& = \sum_{i=1}^N x_i+\sum_{i=1}^N y_i\end{align}$
To summarize:
Rules for manipulating finite series:
constant multiple rule$\displaystyle \sum_{i=1}^N ax_i = a \sum_{i=1}^N x_i$(Eqn 3)
constant addition rule$\displaystyle \sum_{i=1}^N (x_i+b) = Nb + \sum_{i=1}^N x_i$(Eqn 4)
summation over addition rule$\displaystyle \sum_{i=1}^N (x_i+y_i) = \sum_{i=1}^N x_i + \sum_{i=1}^N y_i$(Eqn 5)
It is important to notice that the ∑ symbol means ‘sum the terms immediately to the right’, so
$\displaystyle \sum_{i=1}^3 (x_i + a) = (x_1+ a) + (x_2+ a) + (x_3+ a) = x_1+ x_2+ x_3+ 3a$
but$\displaystyle \sum_{i=1}^3 x_i + a = x_1+x_2+x_3+a$
Sometimes you will see brackets put around the entire summation, but this is usually unnecessary.
For example $\displaystyle a \left(\sum_{i=1}^N x_i\right) = a(x+_1 x_2+ x_3+ \dots + x_N)$
but$\displaystyle a \sum_{i=1}^N x_i$ has the same unambiguous interpretation.
As a second example, note that
$\displaystyle \left(\sum_{i=1}^N x_i\right) + \left(\sum_{i=1}^N y_i\right) = (x_1 + x_2 + x_3 + \dots + x_N)+(y_1 + y_2 + y_3 + \dots + y_N)$ i
but$\displaystyle \sum_{i=1}^N x_i + \sum_{i=1}^N y_i$ has the same interpretation.
Question T3
Use the rules for manipulating the summation symbol to simplify the following expressions; that is, rewrite the expressions in terms of a, b, N, $\displaystyle \sum_{i=1}^N x_i$ and $\displaystyle \sum_{i=1}^N y_i$
(a) $\displaystyle \sum_{i=1}^3 a$ (b) $\displaystyle \sum_{i=0}^2 a$ (c) $\displaystyle \sum_{i=1}^N (ax_i + b)$ (d) $\displaystyle \sum_{i=1}^N (ax_i+by_i)$ (e) $\displaystyle \sum_{i=1}^N (x_i+\langle x \rangle)$ where $\displaystyle \langle x \rangle = \dfrac 1N\sum_{k=1}^N x_k$ i
Answer T3
(a) $\displaystyle \sum_{i=1}^3 a = 3a$ (b) $\displaystyle \sum_{i=0}^2 a = 3a$ (c) $\displaystyle \sum_{i=1}^N (ax_i+b) = Nb + a \sum_{i=1}^N x_i$
(d) $\displaystyle \sum_{i=1}^N (ax_i+by_i) = a \sum_{i=1}^N x_i + b \sum_{i=1}^N y_i $ (e) $\displaystyle \sum_{i=1}^N (x_i+\langle x\rangle) = N \langle x \rangle + \sum_{i=1}^N x_i=2 N \langle x \rangle$
Notice that there is nothing special about the particular summation variable used in a summation, so that, for example, $\displaystyle \sum^N_{i=1} x_i$ can be equally well rewritten as $\displaystyle \sum^N_{k=1} x_k$.
Question T4
Evaluate the following:
$\displaystyle \sum^N_{i=1} 2x_i - \sum^N_{j=1} x_j - \sum^N_{k=1} x_k$ i
Answer T4
We can change all the summation variables to be the same
$\begin{align} \sum_{i=1}^N 2x_i - \sum_{j=1}^N x_j - \sum_{k=1}^N x_k & = \sum_{i=1}^N 2x_i - \sum_{i=1}^N x_i - \sum_{i=1}^N x_i\\& = (2-1-1)\sum_{i=1}^N x_i = 0\end{align}$
Question T5
Show that $\displaystyle \sum_{i=1}^N (x_i-\langle x \rangle)^2 = \sum_{i=1}^N x_i^2 - N\langle x \rangle^2$
remember that, as in Question T2, the mean is defined by:
$\displaystyle \langle x \rangle = \dfrac 1n\sum_{i=1}^N x_i$
Answer T5
We can expand the bracket within the summation to obtain
$\begin{align} \sum_{i=1}^N (x_i+\langle x\rangle)^2 & = \sum_{i=1}^N (x_i^2-2\langle x\rangle x_i+\langle x\rangle^2)\\& = \sum_{i=1}^N x_i^2-2\langle x\rangle \sum_{i=1}^N x_i+N\langle x\rangle^2\\& = \sum_{i=1}^N x_i^2 - 2\langle x\rangle N \langle x\rangle+N\langle x\rangle^2\\& = \sum_{i=1}^N x_i^2 - N \langle x\rangle^2\end{align}$
2.4 Sums of powers of positive integers
It is often an advantage to be able to simplify series such as
$\displaystyle 1 + 2 + 3 + \dots + n = \sum_{i=1}^n i$
or$\displaystyle 5^2 + 6^2 + 7^2 + \dots + n^2 = \sum_{i=5}^n i^2$
n or, more generally, series of the form $\displaystyle \sum_{i=1}^n i^q = 1^q+2^q+3^q+\dots+n^q$, where q is a positive integer i
Although it is possible to derive a general expression for the sum of any such series, irrespective of the (integer) values of q and n, the techniques needed are well beyond the level of this module and the results for the three lowest values of q are probably all you will ever need, so here they are:
$\displaystyle \sum_{k=1}^n k = \dfrac{n(n+1)}{2}$(6)
$\displaystyle \sum_{k=1}^n k^2 = \dfrac{n(n+1)(2n+1)}{6}$(7)
$\displaystyle \sum_{k=1}^n k^3 = \dfrac{n^2(n+1)^2}{4}$(8) i
Question T6
$\displaystyle \sum_{k=1}^n k^3 = \dfrac{n^2(n+1)^2}{4}$(Eqn 8)
Write out the terms in the series $\displaystyle \sum_{k=1}^4 k^3$ and evaluate the sum. Does the result agree with the formula given above?
Answer T6
Writing out the summation explicitly, we have
$\displaystyle \sum_{k=1}^4 k^3 = 1 + 2^3 + 3^3 + 4^3 = 1 + 8 + 27 + 64 = 100$
Using Equation 8,
$\displaystyle \sum_{k=1}^4 k^3 = \dfrac{n^2 (n + 1)^2}{4}$(Eqn 8)
with n = 4, we find
$displaystyle \sum_{k=1}^4 k^3 = \dfrac{n^2 (n + 1)^2}{4} = \dfrac{4^25^2}{4} = 100$
We will omit the proofs of Equations 7 and 8. However, it is easy to derive Equation 6 and doing so provides some valuable practice in using summations.
To begin the proof we consider $\displaystyle 2\sum_{k=1}^n k$ and write it out as two separate sums on two lines (as an ascending and a descending series) in such a way that the sums of various pairs of terms (written one above the other) can be easily seen i:
$\begin{align}2\sum_{k=1}^n k & =~~~~~1~~~~+~~~~2~~~~~+~~~~~3~~~~+\dots+(n-1)+~~~~n~\\& +~~~~~~n~~~~+(n-1)+(n-2)+\dots+~~~~~2~~~~+~~~~1~~~\\ \text{so }2\sum_{k=1}^n k & = \underbrace{(n+1)+(n+1)+(n+1)+\dots+(n+1)+(n+1)}_{\color{purple}{\large n~\text{identical terms}}}\\\text{i.e. }2\sum_{k=1}^n k & = n(n+1)\end{align}$
By arranging the ascending series so that each term is above a complementary term in the descending series it is clear that the sum of each such pair of terms is n + 1. Since there are n such terms it follows that the full sum is n (n + 1), as stated. From this it follows that
$\displaystyle \sum_{k=1}^n k = \dfrac{n(n+1)}{2}$(Eqn 6)
It is often possible to use the summations given in Equations 6, 7 and 8 to solve related problems involving sums of integers. Remember, you can use any other symbol you want in place of k or n provided you make the change consistently throughout the equation.
✦ Simplify the following:
(a) $\displaystyle 5^2 + 6^2 + 7^2 + \dots + n^2 = \sum_{k=5}^n k^2 \quad(n \ge 5)$ (b) $1^2 + 2^2 + 3^2 + \dots + (2n)^2$
✧ (a) $\displaystyle \sum_{k=5}^{n}k^2 = \sum_{k=1}^{n}k^2 - \sum_{k=1}^{4}k^2$
Evaluating the last sum explicitly and using Equation 7, we find
$\displaystyle \sum_{k=5}^{n}k^2 = \sum_{k=1}^{n}k^2 - \sum_{k=1}^{4}k^2$
$\displaystyle \sum_{k=5}^{n}k^2 = \dfrac{n(n+1)(2n+1)}{6}-30$
but a little algebra shows that the right–hand side can be simplified to give
$\displaystyle \sum_{k=5}^{n}k^2 = \dfrac{(n-4)(2n^2+11n+45)}{6}$
(b) $\displaystyle 1^2 +2^2 +3^2 +\dots+(2n)^2 =\sum_{k=1}^{2n} k^2 = \dfrac{n(2n+1)(4n+1)}{3}$
where we have obtained the final expression by replacing n by 2n everywhere in Equation 7.
Question T7
Use rules for manipulating the summation symbol, together with the results for $\sum_{k=1}^n k^q$, to show that
(a) $\displaystyle \sum_{k=1}^n (2k-1) = n^2$ (b) $\displaystyle \sum_{k=1}^n (2k-1)^2 = \dfrac n3(4n^2-1)$
In each case verify your answer for n = 4 by writing out the series and explicitly summing the terms. i
Answer T7
(a) $\displaystyle \sum_{k=1}^n (2k-1) = 2 \sum_{k=1}^n k - \sum_{k=1}^n 1 = 2 \dfrac{n(n+1)}{2}-n=n^2$
For n = 4 we have
$\displaystyle \sum_{k=1}^n (2k-1) = 1 + 3 + 5 + 7 = 16$
which is 42 and therefore consistent with the above result.
$\text{(b) }\begin{align}\sum_{k=1}^n (2k-1)^2 & = \sum_{k=1}^n (4k^2-4k+1)\\& = 4 \sum_{k=1}^nk^2 - 4 \sum_{k=1}^n k + \sum_{k=1}^n 1\\ & = 4\dfrac{n(n + 1)(2n + 1)}{6} - 4 \dfrac{n(n + 1)}{2}+n\\ & = \dfrac n3[2(n + 1)(2n + 1) - 6(n + 1) + 3]\\& = \dfrac n3[(4n^2+ 6n + 2)-(6n + 6) + 3]\\& = \dfrac n3(4n^2-1)\end{align}$
For n = 4 we have
$\displaystyle \sum_{k=1}^n (2k - 1)^2 = 1 + 9 + 25 + 49 = 84$
which is $\dfrac43(4\times 4^2-1)=84$, in agreement with the formula above.
2.5 Arithmetic progressions
A series such as 1 + 3 + 7 + 9 is an example of an arithmetic progression (or arithmetic series). Each term is obtained from its predecessor by adding the same common amount, 2 in this case. Such series are of the general form
a + (a + h) + (a + 2h) + ... + [a + (n − 1)h] which we can write as $\displaystyle \sum_{k=0}^{n-1} (a + kh)$ i
where a is called the first term, h is known as the common difference and there are n terms in the series. We can derive a simple expression for the sum of any arithmetic series by using properties of the summation symbol, together with the result for summing the positive integers
$\displaystyle \sum_{k=0}^{n-1} (a + kh) = \sum_{k=0}^{n-1} a + h \sum_{k=0}^{n-1} k = an +h\dfrac{(n-1)n}{2} = \dfrac n2[2a+(n-1)h]$ i
The last term in the series is [a + (n − 1)h], so if we call this term, b, then we can rewrite the expression above for the sum of an arithmetic progression as
$\dfrac n2[2a+(n-1)h] = \dfrac n2(a+b)$
giving the result
the sum of an arithmetic progression
$\displaystyle \sum_{k=0}^{n-1} (a + kh) = \dfrac n2[2a+(n-1)h] = \dfrac n2(a+b)$(9)
where b = a + (n − 1)h
Notice that n (a + b)/2 is n times the mean (i.e. average) of the first and last terms of the series.
2.6 Geometric progression
A series of the form
a + ar + ar2 + ... + ar n−1 = $\displaystyle \sum_{k=0}^{n-1} ar^k$
is known as a geometric progression (or geometric series) where r is known as the common ratio. Again, a is called the first term and there are n terms in the series. The result of summing the series is
the sum of a geometric progression
$\displaystyle \sum_{k=0}^{n-1} ar^k = \dfrac{a(r^n-1)}{(r-1)}$(10) i
Question T8
(a) Write out in full the terms in the expression
$\displaystyle \sum_{k=0}^3 ar^{k-1} + \sum_{k=4}^4 ar^{k-1}$
and then write the expression as a single sum.
(b) Write out the numbers representing the terms in the series
$\displaystyle \sum_{k=1}^n ar^{k-1}$
for a = 1, r = 2 and n = 4 and find their sum. Does the result agree with Equation 10?
$\displaystyle \sum_{k=0}^{n-1} ar^k = \dfrac{a(r^n-1)}{(r-1)}$(Eqn 10)
Answer T8
(a) $\displaystyle \sum_{k=1}^3 ar^{k-1} + \sum_{k=4}^4 ar^{k-1}= a + ar + ar^2+ ar^3 = \sum_{k=1}^4ar^{k-1}$
This result may be written in the form $\displaystyle \sum_{k=0}^4 ar^k$.
(b) For a = 1, r = 2 and n = 4, we have
$\displaystyle \sum_{k=1}^n ar^{k-1} = \sum_{k=1}^4 2^{k-1} =1+2+4+8=15$
Equation 10 is in agreement with this result since
$\dfrac{a(r^n-1)}{(r-1)} = \dfrac{2^4-1}{(2-1)} = 15$
The method of induction
One way of proving that Equation 10 is the correct formula for the sum of a geometric progression is to use the method of induction_mathematicalinduction. This is a widely applicable technique which consists of showing that if a result is true for some value of a parameter, such as n, then it is also true for (n + 1). Completion of the proof then consists of showing explicitly (and usually trivially) that the result is indeed true for some convenient allowed value of n (usually the smallest allowed value).
$\displaystyle \sum_{k=0}^{n-1} ar^k = \dfrac{a(r^n-1)}{(r-1)}$(Eqn 10)
To prove the result for summing a geometric progression, we start by assuming that the required result is true for a particular, but unspecified, value of n; so that $\displaystyle \sum_{k=0}^{n-1} ar^k = \dfrac{a(r^n-1)}{(r-1)}$ is assumed to be a true statement for this value of n.
We then attempt to show that this implies that the same result must be true for the next value, i.e. n + 1.
We consider the sum with (n − 1) replaced by n, in other words, $\displaystyle \sum_{k=0}^{n} ar^k$, and split it into two parts (as in part (a) of Question T8)
$\displaystyle \sum_{k=1}^n ar^k + \sum_{k=0}^{n-1} ar^k + \sum_{k=n}^n ar^k = \sum_{k=0}^{n-1} ar^k + ar^n$
Notice that the first of these two parts is the sum that we know can be expressed in the desired form, and so
$\begin{align} \sum_{k=0}^{n-1} ar^k + ar^n & = \dfrac{a(r^n-1)}{(r-1)} + ar^n = \dfrac{a(r^n-1) + ar^n(r-1)}{(r-1)}\\& = \dfrac{a[(r^n-1) + (r^{n+1}-r^n)}{(r-1)} = \dfrac{a(r^{n+1}-1)}{(r-1)}\end{align}$
The final result is the same as that given for the sum of a geometric progression, except that (n − 1) is replaced by n. So if the result is true for any particular value of n, it is also true for (n + 1). But, for n = 1, the result is obviously true since
$\displaystyle \sum_{k=0}^0 ar^k = a$
Consequently, the formula is true for n = 2 and therefore n = 3 and therefore n = 4 and so on. Hence the formula for summing a geometric progression has been proved by induction.
Question T9
Simplify the sum $\displaystyle \sum_{k=0}^{n-1} ar^k = a$ if a = 1 and r = 1/3. As n increases, this sum approaches ever closer to a particular value. What is this value?
Answer T9
For a = 1 and r = 1/3, we find
$\displaystyle \sum_{k=0}^{n-1} ar^k = \dfrac{a(r^n-1)}{(r-1)} = \dfrac {\left[\left(\dfrac13\right)^n-1\right]} {\dfrac13-1} =\dfrac32\left[1-\left(\dfrac13\right)^n\right]$
If n is very large $\left(\dfrac13\right)^n$ is very small and the sum is approximately equal to 3/2.
2.7 The binomial expansion
If we have an algebraic expression of the form (a + b)2, then we can easily expand the brackets and collect similar terms
$(a + b)^2= a^2+ 2ab + b^2$
Expanding the expression $(a + b)^3$ is a little harder and gives us
$\begin{align} (a + b)^3 & = (a + b)(a^2+ 2ab + b^2)\\& = (a^3 + 2a^2b + ab^2) + (a^2b + 2ab^2 + b^3)\\& = a^3 + 3a^2b + 3ab^2+ b^3\end{align}$
But what about other expressions of the form (a + b) n? When n is a large integer (i.e. whole number) we clearly need a different technique in order to avoid the tedium of multiplying pairs of brackets and collecting similar terms. We notice that in the expression (a + b)2, if we sum the powers of a and b in each term they are equal to 2. In the same way, for (a+b)3 the sum of the powers of a and bin each term are equal to 3. If we were to continue with (a + b)4, etc. we would always find that the sum of the powers of a and b in each term was equal to the power to which (a + b) was raised.
So, we would find that the expansion of (a + b) n would consist of a series of terms with a and b raised to various powers such that for each term, the sum of the powers of a and b was equal to n. The general term would be a rb n−r, multiplied by a coefficient to be determined. Fortunately there exists a general result, known as the binomial expansion, i which allows us to find these coefficients and which we quote here without proof.
(a+b) n = nCna n + nCn−1a n−1b + nCn−2a n−2b2 + ... + nCn−ra n−rbr + ... + nC1ab n−1 + nC0b n i
i.e. the binomial expansion $\displaystyle (a + b)^n = \sum_{k=0}^n ~^n\!C_{n-k}a^{n-k}b^k$(11)
We must now make a brief diversion in order to understand this result. The symbol, nCr, i where n and r are integers and r ≤ n, is known as a binomial coefficient and is defined by
binomial coefficient
$~^n\!C_r = \dfrac{n(n-1)(n-2)\dots(n-r+2)(n-r+1)}{r(r-1)(r-2) \dots \times 2 \times 1}$ where n ≥ r(12)
✦ Calculate the values of 3C2, 4C2 and 8C3. Why can’t you evaluate 2C3?
✧ With n = 3 and r = 2 we have n − r + 1 = 2, so the final multiplier in the numerator is 2 and Equation 12 gives
$^3\!C_2 = \dfrac{3\times 2}{2\times 1} = 3$
Similarly,$^4\!C_2 = \dfrac{4\times 3}{2\times 1} = 6$
and$^8\!C_3 = \dfrac{8\times 7\times 6}{3\times 2\times 1} = 56$
$^2\!C_3$ cannot be evaluated because it does not satisfy the required condition that n ≥ r.
Notice that the n in nCr is a superscript (that is n is above the C) and is placed in front of the C. You may have already come across the binomial coefficient in another context, since nCr is also the number of ways of choosing r items from n items, irrespective of the order. i
The definition of the binomial coefficient can be written more compactly by using the idea of a factorial. For any positive integer, factorial n (written as n!) is defined by
n! = n (n − 1)(n − 2)(n − 3) ... × 2 × 1 for n ≥ 1(13a)
The definition is completed by defining 0! to be equal to 1.
0! = 1(13b) i
Notice that the factorial of a negative integer is undefined.
Question T10
Calculate n! for n taking each of the values, 0, 1, 2, 3, 4, 5. Describe any feature you can see in these results for n!
Answer T10
0! = 1
1! = 1
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
5! = 5 × 4 × 3 × 2 × 1 = 120
The significant feature of these results is that as n increases, the value of n! increases very quickly. Also each new n! is obtained from the previous one by multiplying it by the new number.
One important property of the factorial is that
(n + 1)! = (n + 1)n!(14)
Notice that the factorial symbol, !, only refers to the immediately preceding expression, so that (n + 1)n! means (n + 1)(n!) and not [(n + 1)n]!
Question T11
Prove the identity i (n + 1)! = (n + 1)n!
Answer T11
From the definition
n! = n (n − 1)(n − 2)(n − 3) ... 2 × 1 for n ≥ 1
we have
(n + 1)! = (n + 1)n (n − 1)(n − 2)(n − 3) ... 2 × 1
= (n + 1)[n (n − 1)(n − 2)(n − 3) ... 2 × 1]
= (n + 1) n!
So, as required
(n + 1)! = (n + 1) n! for n ≥ 0
This is the pattern we commented on in Answer T10.
$\displaystyle ~^n\!C_r = \dfrac{n(n-1)(n-2)\dots(n-r+2)(n-r+1)}{r(r-1)(r-2) \dots \times 2 \times 1}$ where n ≥ r(Eqn 12)
Having introduced the factorial, the binomial coefficient (Equation 12) can now be rewritten as
$\displaystyle ~^n\!C_r = \dfrac{n!}{r!(n-r)!}$(Eqn 15)
We can verify this result by writing the right–hand side of this expression as
$\begin{align} \dfrac{n!}{r!(n-r)!} & = \dfrac{n(n-1)\dots(n-r+1)}{r!(n-r)!}\\& = \dfrac{n(n-1)(n-2)\dots(n-r+2)(n-r+1)}{r(r-1)(r-2) \dots \times 2 \times 1}\end{align}$ i
which is our original definition for the binomial coefficient, nCr.
Question T12
Calculate the values of 1C0, 1C1, 5C3, 10C7, by using Equation 15.
Answer T12
Using $~^n\!C_r = \dfrac{n!}{r!(n - r)!}$
$~^1\!C_0 = \dfrac{1!}{0!1!} = 1$
$~^1\!C_1 = \dfrac{1!}{1!0!} = 1$
$~^5\!C_3 = \dfrac{5!}{3!2!} = \dfrac{5\times 4}{2} = 10$
$~^{10}\!C_7 = \dfrac{10!}{7!3!} = \dfrac{10\times 9\times 8}{3\times 2} = 120$
The binomial coefficient has many properties; some of the most useful are
nCn = 1(16)
nC0 = 1(17)
nCn−r = nCr(18)
nCr = n−1Cr + n−1Cr−1(19)
This is the end of our brief diversion, but before we return to the binomial expansion, try the following exercise
Question T13
Prove the following identities: nCn = 1, nC0 = 1, and nCn−r = nCr
Answer T13
Using $~^n\!C_r = \dfrac{n!}{r!(n - r)!}$ and the fact that 0! = 1, we have
$~^n\!C_n = \dfrac{n!}{n!0!} = 1~~~\text{and}~~~^n\!C_0 = \dfrac{n!}{0!n!} = 1$
To derive the third result, consider
$~^n\!C_{n-r} = \dfrac{n!}{[(n - (n-r)]!(n-r)!} = \dfrac{n!}{(n-r)!r!} = ~^n\!C_r$
Now that we understand what is meant by the nCr symbol, we can use the binomial series of Equation 11 to write down the expansion of any expression of the form (a + b) n. For example, (1 + x)6 can be written
$\begin{align} (1+x)^6 & = \sum_{k=0}^6 \dfrac{6!}{k!(6-k)!}x^k\\& = 1+6x+\dfrac{6\times 5}{2\times 1}x^2 + \dfrac{6\times 5\times 4}{3\times 2\times 1}x^3 + \dfrac{6\times 5}{2\times 1}x^4 + 6x^5 + x^6\\& = 1+6x+15x^2 +20x^3 +15x^4 +6x^5 +x^6\end{align}$(20)
Question T14
Verify Equation 20 by explicitly multiplying out brackets and collecting similar terms.
Answer T14
There are many ways of explicitly multiplying out the brackets. One possibility is to work out
(1 + x)2 = (1 + x)(1 + x) = 1 + x + x + x2 = 1 + 2x + x2
and next
(1 + x)3 = (1 + x)(1 + x)2 = (1 + x)(1 + 2x + x2) = 1 + 3x + 3x2 + x2
and finally
(1 + x)6 = (1 + x)2(1 + x)2 = (1 + 3x + 3x2 + x2)(1 + 3x + 3x2 + x2)
= (1 + 3x + 3x2 + x2) + (3x + 9x2 + 9x2 + 3x2) + (3x2 + 9x2 + 9x2 + 3x2) + (x2 + 3x2 + 3x2 + x2)
= 1 + 6x + 15x2 + 20x2 + 15x2 + 6x2 + x2
which is in agreement with the binomial expansion.
This should convince you that it is worth knowing the binomial expansion! If you are still not convinced, try using explicit multiplication to work out (1 + x)12.
3 Infinite series
Infinity is not a number but this does not prevent us from using phrases such as ‘sum to infinity’ and ‘infinite series’, nor does it prevent us from using an infinity symbol ∞ to represent infinity, provided that we have a clear understanding of what they mean.
For example, for any specified integer n, the sum
$\displaystyle \sum_{k=1}^n \dfrac{1}{2^{k-1}} = 1+\dfrac12+\dfrac14+\dots+\dfrac{1}{2^{n-1}}$(21)
represents a specific number. When n is 1 this number is 1, when n is 2 the number is 3/2, and so on. Now, the series represented by Equation 21 is a geometric progression with first term 1 and common ratio 1/2, so, according to Equation 10, its sum is
$\displaystyle \sum_{k=1}^n \dfrac{1}{2^{k-1}} = \dfrac{\left(\dfrac{1}{2^n}-1\right)}{\dfrac12-1} = 2\left(1-\dfrac{1}{2^n}\right)$
Notice that $\dfrac{1}{2^n}$ can be made as small as we please by choosing n sufficiently large. In other words, we can make the sum as close to 2 as we please provided that we take a sufficiently large number of terms in the series. In such a case we write
$\displaystyle \sum_{k=1}^n \dfrac{1}{2^{k-1}} = 2$
and we say that the left–hand side is ‘an infinite series’ and ‘the sum to infinity is 2’. We may also write
$1+\dfrac12+\dfrac14+\dfrac18+\dots = 2$
We are not suggesting that an infinite ‘number’ i of additions will give the number 2, but merely that we can get as close to 2 as we like by performing a sufficiently large number of additions.
3.1 Some standard infinite series
Infinite series, or even parts of infinite series, are of great importance in physics since they can often be used to represent functions, including such basic functions as exp(x), loge(x), sin(x) and cos(x). The infinite series corresponding to a particular function can often be derived from a very general series called a Taylor series (or Taylor expansion). i This powerful technique for finding series representations requires a good knowledge of calculus and is therefore beyond the scope of this module, though it is treated elsewhere in FLAP. Nonetheless, some of the results that Taylor series provide are well within the coverage of this module and they are quoted below without proof.
Some useful infinite series i
$\displaystyle \exp(x) = \sum_{n=0}^{\infty} \dfrac{x^n}{n!} = 1 + \dfrac{1}{1!} + \dfrac{1}{2!} + \dfrac{1}{3!} + \dots~~\text{for all}~x$(22)
$\displaystyle \sin(x) = \sum_{n=0}^{\infty} \dfrac{(-1)^nx^{2n+1}}{(2n+1)!} = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \dots~~\text{for all}~x$(23)
$\displaystyle \cos(x) = \sum_{n=0}^{\infty} \dfrac{(-1)^nx^{2n}}{(2n)!} = x - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \dots~~\text{for all}~x$(24)
$\displaystyle \loge(1-x) = \sum_{n=1}^{\infty} \dfrac{x^n}{n} = -x - \dfrac{x^2}{2} - \dfrac{x^3}{3} - \dfrac{x^4}{4} - \dots~~\text{for}~-1 \le x \lt 1$(25)
and for any real number r:
$\displaystyle (1+x)^r = 1 + \dfrac{rx}{1!} + \dfrac{r(r-1)x^2}{2!} + \dfrac{r(r-1)(r-2)x^3}{3!} + \dots~~\text{for}~-1 \lt x \lt 1$(26) i
Equation 26 is often known as the binomial series. Notice that the series for (1 + x) r is similar to the binomial expansion, but is more general in the sense that r is not necessarily an integer. i In each of the above cases we are claiming that, for a fixed value of x in the allowed range, any desired accuracy may be obtained by taking a sufficiently large number of terms in the series.
All the series given above are series in powers of x; that is, each term in the series involves a factor of the form x n, for some whole number n. Such series are often referred to as power series or series expansions. Series which involve powers of expressions are also possible. For example, replacing x by (1 − x) in the series for the logarithmic function gives
$\begin{align} \loge(x) & = -\sum_{n=1}^{\infty} \dfrac{(1-x)^n}{n}\\& = -(1-x)-\dfrac{(1− x)^2}{2}-\dfrac{(1-x)^3}{3}-\dfrac{(1-x)^4}{4}+\dots\end{align}$
and the series on the right–hand side of this equation can be used to approximate the values of loge(x) provided that 0 < x ≤ 2.
✦ Why are the values of x in the above form of the logarithmic series limited to the range 0 < x ≤ 2? i
✧ Because the series from which it was derived (Equation 25) was only valid if −1 ≤ x < 1, so when we replaced (1 − x) by x in Equation 25 we effectively introduced a new variable (even though we called it x) that was obtained by reversing the sign of the original x variable and then adding 1. The effect of these operations on the range of the original x variable is to produce the given range for the new variable. (This process was illustrated in Question R1).
Question T15
$(1+x)^r = 1 + \dfrac{rx}{1!} + \dfrac{r(r-1)x^2}{2!} + \dfrac{r(r-1)(r-2)x^3}{3!} + \dots~~\text{for}~-1 \lt x \lt 1$ (Eqn 26)
Use the binomial series for (1 + x) r given in Equation 26 to express the function
f (x) = (1 + x)−1
as a series in powers of x, simplifying the resulting expression as far as you can. Can this series be used to
approximate the value of $\dfrac{1}{1+\pi}$ by putting x = π?
Answer T15
Setting r equal to −1 in the series
$(1+x)^r = 1 + \dfrac{rx}{1!} + \dfrac{r(r-1)x^2}{2!} + \dfrac{r(r-1)(r-2)x^3}{3!} + \dots$ for −1 < x < 1
For r = −1 we obtain
$\begin{align} (1+x)^{-1} & = 1 + \dfrac{(-1)}{1!}x + \dfrac{(-1)(-2)}{2!}x^2 + \dfrac{(-1)(-2)(-3)}{3!}x^3 + \dots\\& = 1-x+x^2-x^3+x^4 + \dots\\& = \sum_{n=0}^{\infty} (-1)^nx^n~~~~\text{for}~~-1 \lt x \lt 1\end{align}$
We cannot put x = π and obtain a good approximation for (1 + π)−1since π does not lie in −1 < x < 1.
Comment Notice that, for this special case of r = −1, the series for (1 + x) r is a geometric series with common ratio −x.
The series given in Equations 22 to 26 allow us to derive many useful properties of the functions that they represent. Indeed, it is often convenient to take the view that the series actually define the associated functions. So, if you want to know the meaning of a specific quantity such as exp(2) = e2, a perfectly legitimate answer is
$\displaystyle \exp(2) = \sum_{n=0}^{\infty} \dfrac{2^n}{n!} = 1+\dfrac{2}{1!}+\dfrac{2^2}{2!}+\dfrac{2^3}{3!}+\dots = 1 +2+2+\dfrac43+\dots$
Whatever value your calculator gives for exp(2) will be reproduced by the series, provided you add up enough terms. (Indeed, your calculator probably evaluates exp(2) by summing such a series internally.)
Moreover, the series are not only limited to providing numerical results, but they can also provide insight of a more algebraic nature.
For example, the sine function is an odd function, i.e. it has the property that sin(−x) = −sin(x), and this is reflected in the power series for sin(x) which contains only odd powers of x that will also change sign if x is replaced by −x.
Similarly, cos(x) is an even function since cos(−x) = cos(x) and its series is composed of even powers of x. i
Apart from transforming a given series by substituting some algebraic expression in place of x it is also possible to change the appearance of the series by altering the summation variable and adjusting the upper and lower limits of the summation. Here is an example.
If we have $\displaystyle \sum_{n=1}^{\infty} \dfrac{x^{n-1}}{(n-1)!}$ then we can introduce a new summation variable, m, defined by m = n − 1; the series can then be written as $\displaystyle \sum_{n=1}^{\infty} \dfrac{x^{n-1}}{(n-1)!}$ where the summation starts at 0, since n = 1 corresponds to m = 0. There is nothing special about the symbol m, any other symbol would do equally well, so we may replace m by n and obtain $\displaystyle \sum_{n=0}^{\infty} \dfrac{x^n}{n!}$
Question T16
Write the following series so that the summations start at n = 0. Identify which well known functions are represented by each series
(a) $\displaystyle \sum_{k=1}^{n+1}~^n\!C_{n-k+1}a^{n-k+1}b^{k-1}$ (b) $\displaystyle -\sum_{n=1}^{\infty} \dfrac{(-1)^nx^{2n-1}}{(2n-1)!}$
Answer T16
(a) If we set (k − 1) = m in $\displaystyle \sum_{k=1}^{n+1} ~^n\!C_{n-k+1} a^{n-k+1}b^{k-1}$
and realize that
k = 1 implies m = 0
k = n + 1 implies m = n
andn − k + 1 = n − (m + 1) + 1 = n − m
we obtain $\displaystyle \sum_{m=1}^{n}~^n\!C_{n-m} a^{n-m}b^{m}$
This is the binomial series for (a + b)2.
(b) If we set (n − 1) = m in $\displaystyle -\sum_{n=1}^{\infty} \dfrac{(-1)^nx^{2n-1}}{(2n-1)!}$
and realize that n = 1 implies m = 0
and2n − 1 = 2 (m + 1) − 1 = 2m + 1
$\begin{align}\text{we obtain}~~~~-\sum_{n=1}^{\infty} \dfrac{(-1)^nx^{2n-1}}{(2n-1)!} & = -\sum_{m=0}^{\infty} \dfrac{(-1)^{m+1}x^{2m+1}}{(2m+1)!}\\ & = \sum_{m=0}^{\infty} \dfrac{(-1)^mx^{2m+1}}{(2m+1)!}\end{align}$
This is the series for sin(x).
Question T17
Using the series you have already been given, find a power series for $\dfrac{1}{1-x}$. Write down the first four terms explicitly and then write down the series in a compact way using the ∑ symbol with a lower limit of 0.
Answer T17
We can obtain the series from Equation 26 with r = −1 and x replaced by −x
Thus,(1 − x)−1 = 1 + x + x2 + x3 + ... for −1 < x < 1
i.e.(1 − x)−1 = $\displaystyle \sum_{i=0}^{\infty} x^i$ for −1 < x < 1
3.2 Convergence and divergence: the ratio test i
Study comment This subsection is rather more technical than the rest of the module. Its main conclusions are that not all infinite series are well defined and that those infinite series which do represent functions are often only well defined when the variable is restricted to a specific range of values. In fact, this subsection provides only a brief introduction to its topic. In particular, it does not deal with what are known as oscillating or conditionally convergent series and it gives only one of many possible tests for convergence.
In order to discuss in more detail the circumstances for which infinite series are meaningful, we need to introduce the concept of a partial sum. If we consider an infinite series
$\displaystyle \sum_{k=1}^{\infty} a_k = a_1+a_2+a_3+a_4+\dots$
then the sum of the first n terms is known as a partial sum. Such a sum may be denoted by Sn, in which case
$\displaystyle S_n = \sum_{k=1}^n a_k = a_1+a_2+a_3+a_4+\dots+a_n$
So, for example, if we have the infinite series
$\displaystyle \sum_{k=1}^{\infty} \left(\dfrac12\right)^{k-1} = 1 + \dfrac12+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dots$
then the first few partial sums are
S1 = 1.0
S2 = 1.5
S3 = 1.75
S4 = 1.875
S5 = 1.906 25
Question T18
It can be shown that the constant, π2, is given by the following infinite series
$\displaystyle \pi^2 = 6 \sum_{n=1}^{\infty} \dfrac{1}{n^2} = 6\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+\dots\right)$
Evaluate the first five partial sums $\displaystyle S_1 = 6 \sum_{n=1}^1 \dfrac{1}{n^2}, S_2 = 6 \sum_{n=1}^2 \dfrac{1}{n^2}$ and so on, and comment on the difference between these partial sums and the value of π2 given by your calculator.
Answer T18
The partial sums are
$S_1=6$
$S_2=6\left(1 + \dfrac14\right) = 7.5$
$S_3=6\left(1 + \dfrac14 + \dfrac19\right) = 8.17$
$S_4=6\left(1 + \dfrac14 + \dfrac19 + \dfrac{1}{16}\right) = 8.54$
$S_5=6\left(1 + \dfrac14 + \dfrac19 + \dfrac{1}{16} + \dfrac{1}{25}\right) = 8.78$
Calculating π2 − Sk we find
π2 − S1 ≈ 3.87
π2 − S2 ≈ 2.37
π2 − S3 ≈ 1.70
π2 − S4 ≈ 1.33
π2 − S5 ≈ 1.09
These values get smaller as k increases. Therefore, it seems likely that the partial sums get closer to π2 as k increases. (A detailed analysis shows that this is correct.)
Convergent and divergent sequences
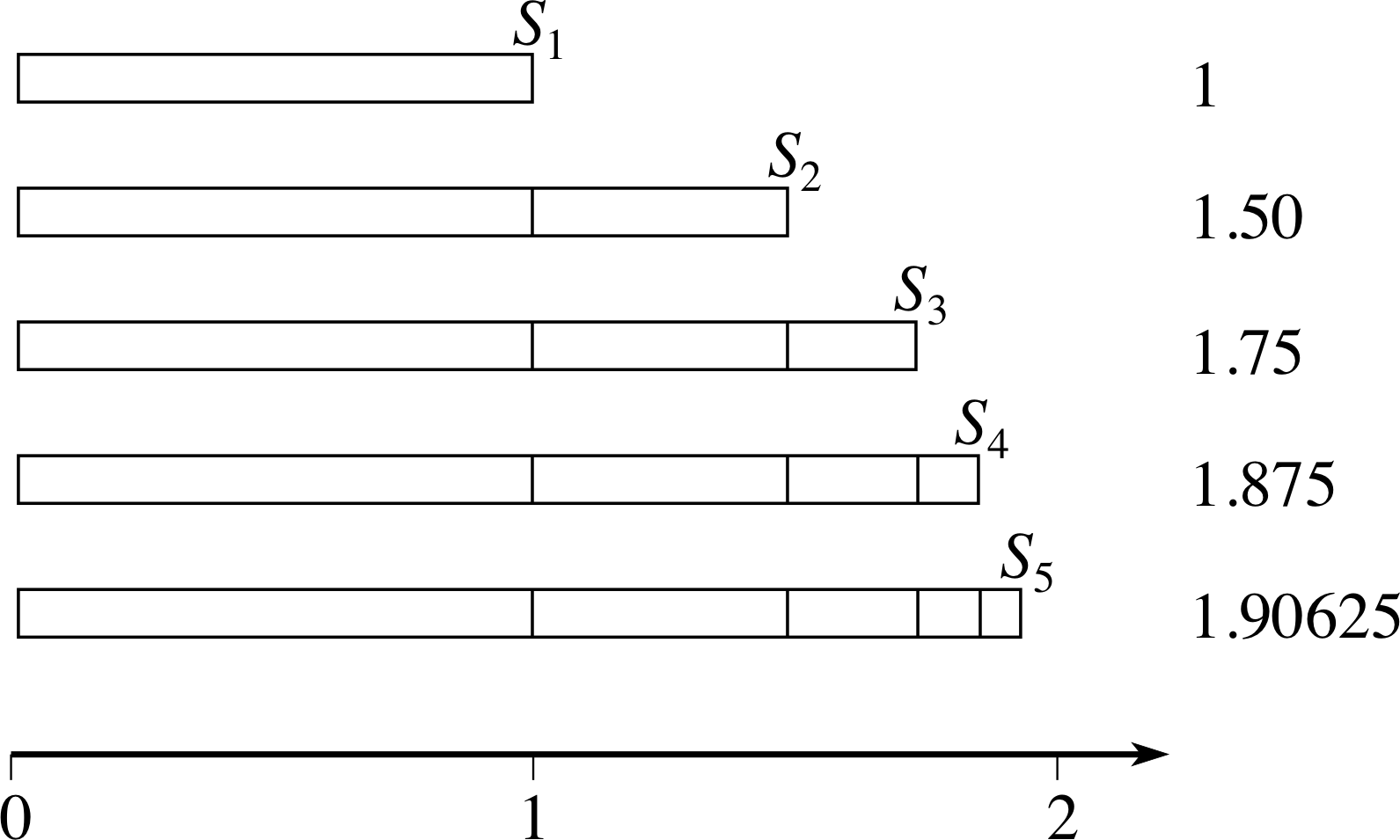
Figure 1 Sequence of terms, Sn, defined by $\displaystyle S_n = \sum_{k=1}^n \left(\dfrac12\right)^{k-1}$.
We can now define what we mean by a convergent sequence. The infinite sequence, a1, a2, a3, a4, ... is said to converge if we can always find some member of the sequence such that all other members beyond it are as close as we choose to some particular value. This value is called the limit of the sequence.
This is a very formal definition, but some insight can be obtained by looking at Figure 1, which shows the sequence of partial sums we worked out earlier, S1, S2, S3, .... In this particular case, if we examine the members of the sequence one after the other, then we move progressively to the right, with the difference between each step being half the previous step. We saw earlier (at the beginning of Section 2) that the limit of this sequence is equal to 2, and if we choose a particular value as close as we wish to 2 (say 1.90) then we can find a member of the sequence Sn such that all later members of the sequence, i.e. all Si with i > n, are between 1.90 and 2. In this particular case n = 5, but if we had chosen some other value closer to 2, such as 1.99, there would still have been some corresponding value of n. i
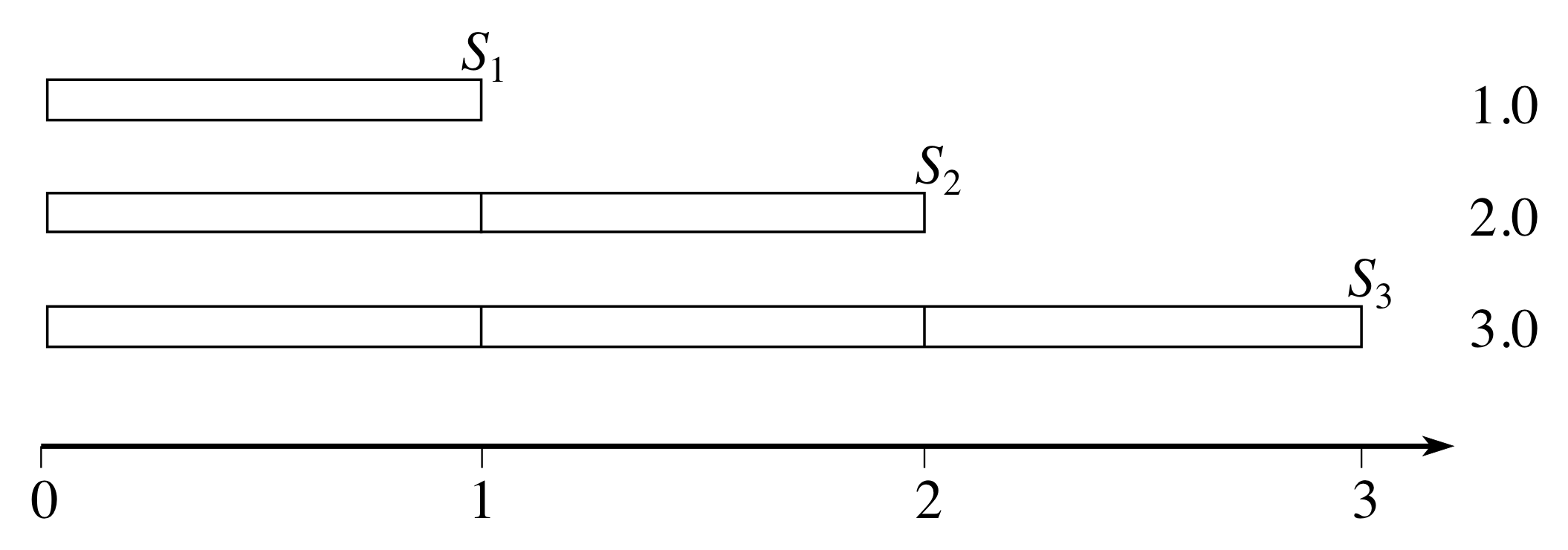
Figure 2 Sequence of terms, Sn, defined by Sn = n.
Some sequences do not converge. A sequence which does not converge is known as a divergent sequence. As an example, the sequence defined by
Sn = n for n = 1, 2, 3, ...
is divergent.
If you look at Figure 2 you can see that this sequence diverges since the members of the sequence are equally spaced along a line, with no sign of any limit (in contrast to Figure 1).
✦ What is the limit of the sequence $S_n = \dfrac{(n+1)^2}{n^2}$?
✧ Since $\displaystyle S_n=\dfrac{n^2+2n+1}{n^2}=1+\dfrac 2n+\dfrac{1}{n^2}$
we have $\displaystyle \lim_{n\rightarrow\infty}(S_n)=\lim_{n\rightarrow\infty} \left(1+\dfrac 2n+\dfrac{1}{n^2}\right)=1$
Convergent and divergent series
Now that you know what is meant by a convergent sequence and a partial sum, we can define a convergent series. An infinite series is said to converge if the partial sums of the series form a convergent sequence. The limit of the sequence of partial sums is known as the sum of the series. So the series
$\displaystyle \sum_{k=1}^{\infty} \left(\dfrac12\right)^{k-1} = 1 + \dfrac12+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dots$
is an example of a convergent series and the sum of this series is 2.
Not all series are convergent; any series which does not converge is said to be a divergent series.
An example of a divergent series is
$\displaystyle \sum_{n=0}^{\infty} 1 = 1+1+1+1+1+1+1+\dots$
since the partial sums increase without limit.
It is evident that for a series $\displaystyle \sum_{n=1}^{\infty} a_n$ to converge the individual terms must approach zero as n tends to infinity. We can use a piece of standard mathematical notation to signify this requirement by writing, $\displaystyle \lim_{n\rightarrow\infty} (a_n) = 0$.
(This may be read as ‘an tends to 0 in the limit as n tends to infinity’.) However, the converse is not true, there are many divergent series for which $\displaystyle \lim_{n\rightarrow\infty} (a_n) = 0$.
How then can we tell if a series is convergent or divergent? For example, does the following series converge?
$\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n!} = 1 + \dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!}+\dfrac{1}{5!}\dots$
It is not always easy to tell if a series converges but there are a number of possible tests. Here we only consider one test, limited to series that consist of positive terms, as an example of the techniques involved.
D’Alembert’s ratio test
Suppose we have a series of positive terms of the form $\displaystyle \sum_{n=1}^{\infty} a_n$, then d’Alembert’s ratio test i requires us to calculate the ratio of successive terms, an+1/an, and then determine the limit of this quantity as n tends to infinity.
If we call this limit R we can write
$\displaystyle R = \lim_{n\rightarrow\infty}\left(\dfrac{a_{n+}1}{a_n}\right)$
and the ratio test then tells us that:
if R < 1 the series is convergent,
if R > 1 the series is divergent, and
if R = 1 the test fails.
✦ Use the d’Alembert’s ratio test to determine which of the following series converge
(a) $\displaystyle \sum_{n=1}^{\infty} \left(\dfrac12\right)^{k-1} = 1 + \dfrac12+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dots$ (b) $\displaystyle \sum_{n=1}^{\infty} n! = 1 + 2! + 3! + 4! + \dots$ (c) $\displaystyle \sum_{n=1}^{\infty} n$
✧ Applying the d’Alembert’s ratio test, we find
(a) $\displaystyle R = \lim_{n\rightarrow\infty} \left(\dfrac{a_{n+1}}{a_n}\right) = \lim_{n\rightarrow\infty} \left(\dfrac12\right)^{n+1}\left(\dfrac12\right)^{-n} = \dfrac12 \lt 1$
and the series converges, in agreement with our previous discussion.
(b) $\displaystyle R = \lim_{n\rightarrow\infty} \left[\dfrac{(n+1)!}{n!}\right] = \lim_{n\rightarrow\infty};(n+1) = \infty$
Since R is greater than 1, this series diverges. This is not very surprising as the terms get very large as n tends to infinity.
(c) $\displaystyle R = \lim_{n\rightarrow\infty} \left(\dfrac{a_{n+1}}{a_n}\right) = \lim_{n\rightarrow\infty} \left(\dfrac{n+1}{n}\right) = \lim_{n\rightarrow\infty} \left(1+\dfrac 1n\right) = 1 + \lim_{n\rightarrow\infty} \left(\dfrac 1n\right) = 1 + 0 = 1$
So in this case the test fails, it is not sufficiently sensitive and it doesn’t tell us whether or not the series converges. In fact, since $\displaystyle \lim_{n\rightarrow\infty} (a_n) \ne 0$ the series is divergent.
Question T19
Use d’Alembert’s ratio test to discover whether or not the following series is convergent
$\displaystyle \sum_{n=1}^{\infty} \dfrac{n}{(n+1)!} = \dfrac{1}{2!}+\dfrac{2}{3!}+\dfrac{3}{4!}+\dfrac{4}{5!}+\dots$
Answer T19
If we define $a_n = \dfrac{n}{(n+1)!}$, then
$\begin{align} R & = \lim_{n\rightarrow\infty} \left(\dfrac{a_{n+1}}{a_n}\right) = \dfrac{(n + 1)}{(n+2)!}\dfrac{(n + 1)!}{n}\\& = \lim_{n\rightarrow\infty} \left[\dfrac{(n+1)}{n(n+2)}\right] = \lim_{n\rightarrow\infty} \left[\dfrac{\dfrac 1n+\dfrac{1}{n^2}}{\left(1+\dfrac 2n\right)}\right] = 0\end{align}$
Since R < 1, this series is convergent.
Question T20
For what non–negative values of x does the following series converge?
$\displaystyle \exp(x) = \sum_{n=1}^{\infty} \dfrac{x^n}{n!} = 1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dots$
Give reasons for your conclusion.
Answer T20
If we define $a_n = \dfrac{x^n}{n!}$
then, applying d’Alembert’s ratio test for convergence, we need R < 1 where
$\displaystyle R = \lim_{n\rightarrow\infty} \left(\dfrac{a_{n+1}}{a_n}\right) = \dfrac{x^{n+1}}{(n+1)!}\dfrac{n!}{x^n}$
$\displaystyle R = \lim_{n\rightarrow\infty} \left(\dfrac{x}{n+1}\right) = 0$
for all finite values of x. D’Alembert’s test only applies for series of positive terms, so we have only shown that the series converges for 0 ≤ x < ∞. It can be shown that the series also converges for all negative values of x.
3.3 Approximations to infinite series
If we truncate (i.e. terminate) a series at some point, then it may provide a useful approximation to the complete series, but the truncated series is only useful if the discarded terms are in some sense ‘small’. For example, it can be shown that the constant, π, is given by
$\pi = 4\left(1-\dfrac13+\dfrac15-\dfrac17+\dfrac19+\dots\right)$
Truncating the series at the third term, we get
$\pi = 4\left(1-\dfrac13+\dfrac15\right) = 3.47$
This is a rather poor approximation to the value of π, but can be improved by including further terms in the series. Alternatively, there are other series which give good approximations to π by summing comparatively few terms.
Question T21
It can be shown that the constant, π, is also given by
$\displaystyle \dfrac{\pi^4}{96} = \sum_{n=0}^{\infty} \dfrac{1}{(2n+1)^4} = 1 + \dfrac{1}{3^4}+\dfrac{1}{5^4}+\dfrac{1}{7^4}+\dfrac{1}{9^4}+\dfrac{1}{11^4}+\dots$
Use the first five terms in this series to obtain an approximation to π. What is the percentage error in your value when compared with the value of π given on your calculator?
Answer T21
Using the first five terms, we find
$\dfrac{\pi^4}{96} = 1+ \dfrac{1}{3^4} + \dfrac{1}{5^4} +\dfrac{1}{7^4} +\dfrac{1}{9^4} \approx 1.014\,515$
So,π ≈ (96 × 1.014 514)1/4 ≈ 3.141 47
and the percentage error is $\dfrac{\pi - 3.141\,47}{\pi}$ × 100% ≈ 0. 004%
The value of π given by a calculator (or in mathematical tables) is not exact; it has been calculated using an approximation, such as the first few terms in an infinite power series. So you may be wondering how to use a series to find an approximation to a specified accuracy. A rough ‘rule of thumb’ is to keep calculating until the next term in the series is less than the error you are willing to tolerate. However, further analysis of the particular series is required in order to make a precise statement.
Series can also give useful approximations to functions. For example, from Subsection 3.1 (Equation 23) we have the following series for sin(x)
$\displaystyle \sin(x) = \sum_{n=0}^{\infty} \dfrac{(-1)^nx^{2n+1}}{(2n+1)!} = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \dots~~\text{for all}~x$(Eqn 23)
The series converges for all values of x. However for large values of x we may have to take a considerable number of terms in order to obtain a good approximation. On the other hand, for small values of x we need very few terms. The simple approximations
$\sin(x) \approx x - \dfrac{x^3}{3!}$(27)
$\cos(x) \approx 1 - \dfrac{x^2}{2!}$(28)
have applications in many areas of physics. By ‘small values of x’ in the context of Equation 27, for example, we mean that x3 is much smaller than x (which we sometimes write as x3 ≪ x). Whether or not this rather crude approximation is justified in a particular case will depend on the application you have in mind.
Question T22
Using your calculator plot a graph of $E(x) = \dfrac{100\%(x-\sin(x))}{\sin(x)}$ for 0 < x ≤ 0.3
E (x) is the percentage error that occurs in the value of sin(x) if you assume that sin(x) ≈ x. From your graph estimate the value of a such that if x > a then the percentage error in the approximation sin(x) ≈ x is more than 1%. By approximating $\sin(x)\approx-\dfrac{x^3}{3!}$, or otherwise, find an algebraic estimate for a.
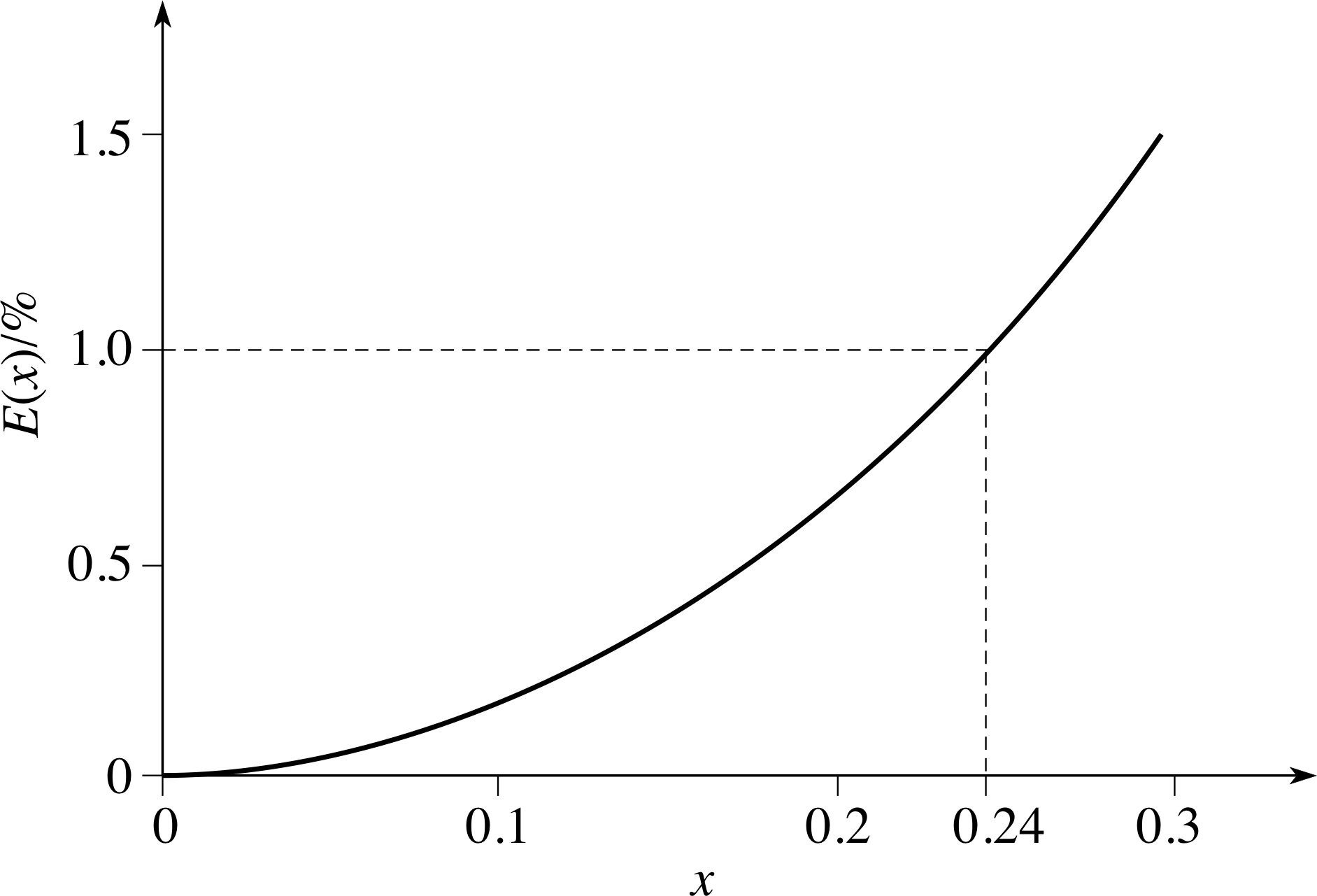
Figure 3 See Answer T22.
Answer T22
$E(x) = \dfrac{100\%[x - \sin(x)]}{\sin(x)}$
where x is the angle/radians. Plotting E (x) against x, gives us Figure 3, from which we find that an error of 1% occurs for x = a ≈ 0.24.
By extending Figure 3 to larger values of x, you can convince yourself that the error continues to increase as x increases.
From the series
$\sin(x)=\sum_{n=0}^{\infty} \dfrac{(-1)^nx^{2n+1}}{(2n+1)!} \approx x - \dfrac{x^3}{3!}$
so that$E(x) = 100\%\left[\dfrac{x}{x-(x^3/3!)}\right] = 100%\left(\dfrac{x^2}{6-x^2}\right)$
the value of x for which the error is 1% is given approximately by
$100\left(\dfrac{x^2}{6-x^2}\right) = 1$
Thus,$a \approx \sqrt{\dfrac{6}{101}\os} \approx 0.2437$
We should really show directly from the series that the error increases as x increases, but this is beyond the scope of this module.
Comment A more accurate value is a = 0.244 097 which can be obtained by solving the equation
$100\left(\dfrac{x}{\sin x}-1\right) = 1$
using a numerical procedure such as the Newton–Raphson method, but that is also beyond the scope of this module.
✦ Use the power series given in Equations 22 to 26 to find a series expansion of sin(2x) cos(x) up to and including terms involving x3.
✧ Equations 23 and 24 imply that up to terms involving x3
$ \sin(2x) \approx 2x - \dfrac{(2x)^3}{3!}~~~\text{and}~~~\cos(x) \approx 1-\dfrac{x^2}{2!}$
Multiplying these two truncated series together gives us
$ \sin(2x) \cos(x) \approx \left[2x-\dfrac{(2x)^3}{3!}\right]\left[1-\dfrac{x^2}{2!}\right] \approx 2x - \dfrac{7x^3}{3}+\dfrac{2x^5}{3}$
So, up to and including powers of x3
$ \sin(2x) \cos(x) \approx 2x - \dfrac{7x^3}{3}$
Note that in obtaining the last result it was important to use approximations that included the appropriate number of terms. For instance, if we had simply approximated sin(2x) by 2x we would have obtained a different (incorrect) result. However, if we had included any additional terms in the approximations to sin(2x) or cos(x) they would not have made any difference to the final result (up to terms in x3).
✦ Considering only terms up to (and including) x2, find an approximate solution to the equation
ex + cos(x) = 1
✧ Equations 22 and 24
$\displaystyle \exp(x)=\sum_{n=0}^{\infty} \dfrac{x^n}{n!}=1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dots$ for all x(Eqn 22)
$\displaystyle \cos(x)=\sum_{n=0}^{\infty} \dfrac{(-1)^nx^{2n}}{(2n)!}=1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\dfrac{x^6}{6!}+\dots$ for all x(Eqn 24)
imply that up to terms involving x2
$e^x \approx 1 + x + \dfrac{x^2}{2} \quad\text{and}\quad\cos(x) \approx 1 - \dfrac{x^2}{2}$
So, adding these two truncated series together, up to terms involving x2, we find
$1 + x + \dfrac{x^2}{2} + 1 - \dfrac{x^2}{2} \approx 1$ i
i.e.2 + x ≈ 1
It follows that x ≈ −1
Another approximation which is often useful can be obtained by taking the first two terms of the binomial theorem
$(1+x)^r = 1 + \dfrac{rx}{1!} + \dfrac{r(r-1)x^2}{2!} + \dfrac{r(r-1)(r-2)x^3}{3!} + \dots$ for −1 < x < 1
i.e.(1 + x) r ≈ 1 + rx for | x | < 1(29)
As a simple example, we can use this expression to relate the so–called linear and volume coefficients of thermal expansion (α and β, respectively). i The length l, of an object at temperature T, is given by
l = l0(1 + αT)
where l0 is the length when the temperature is zero and α is a constant for the material. If we consider the volume V of a cube with each side of length l, at temperature T, we find
V = l 3 = l03( 1 + αT)3
and if we let V0 = l0, the volume at temperature zero, we have (using Equation 29)
V = V0(1 + αT)3 ≈V0(1 + 3αT)
But the volume V, of an object at temperature T, is also given by
V = V0(1 + βT) i
and therefore we have the relation
β ≈ 3α
Question T23
According to Einstein’s special theory of relativity, the total relativistic energy E, of a particle of mass m, moving freely with speed v is given by:
$E = \dfrac{mc^2}{\sqrt{1-\dfrac{v^2}{c^2}}}$
where m and c are constants (c is the speed of light in a vacuum). Use the first two terms in the series expansion of (1 + x) r to show that, for v2 < c2, E can be written as
E ≈ E0 + T
where E0 is a constant and T is a function of v, whose form you should determine.
Answer T23
From the series
$(1+x)^r = 1 + \dfrac{rx}{1!} + \dfrac{r(r-1)x^2}{2!} + \dfrac{r(r-1)(r-2)x^3}{3!} + \dots$ for −1 < x < 1
With r = −1/2 we find
(1 + x)−1/2 ≈ 1 − (x/2) when x is small.
Replacing x by $-\dfrac{v^2}{c^2}$, we can use this result to write
$E = \dfrac{mc^2}{\left(1-\dfrac{v^2}{c^2}\right)^{1/2}} \approx mc^2\left(1+\dfrac{v^2}{2c^2}\right) \approx mc^2 + \dfrac{mv^2}{2}$
Since$v^2 \lt c^2$ implies that $0 \lt \dfrac{v^2}{c^2}\lt 1$
Thus,E0 = mc2 and T = ½mv2
where T is the kinetic energy of a particle, as defined in Newtonian mechanics.
(In the special theory of relativity the kinetic energy is defined to be E − E0, so the Newtonian expression is only a low speed approximation to the (relativistic) kinetic energy.
4 Closing items
4.1 Module summary
- 1$\vphantom{\displaystyle \sum_{n=1}^N}$
-
The Subsection 2.3summation symbol, as for example in $\displaystyle \sum_{n=1}^N n = 1 + 2 + 3 +\dots+ N$, is a convenient shorthand notation and it has the following properties
$\displaystyle \sum_{i=1}^N ax_i = a\sum_{i=1}^N x_i$(Eqn 3)
$\displaystyle \sum_{i=1}^N (x_i+b) = Nb + \sum_{i=1}^N x_i$(Eqn 4)
$\displaystyle \sum_{i=1}^N (x_i+y_i) = \sum_{i=1}^N x_i+\sum_{i=1}^N y_i$(Eqn 5)
- 2
-
Standard sums that are frequently of use include:
$\displaystyle \sum_{k=1}^n k = \dfrac{n(n+1)}{2}$(Eqn 6)
$\displaystyle \sum_{k=1}^n k^2 = \dfrac{n(n+1)(2n+1)}{6}$(Eqn 7)
$\displaystyle \sum_{k=1}^n k^3 = \dfrac{n^2(n+1)^2}{4}$(Eqn 8)
the Subsection 2.5arithmetic progression with common difference h
$\displaystyle \sum_{k=0}^{n-1} (a + kh) = \dfrac n2[2a+(n-1)h]$(Eqn 9)
the Subsection 2.6geometric progression with common ratio r
$\displaystyle \sum_{k=0}^{n-1} ar^k = \dfrac{a(r^n-1)}{(r-1)}$(Eqn 10)
and the Subsection 2.7binomial expansion
$\displaystyle (a+b)^n = \sum_{k=0}^n~^n\!C_{n-k}a^{n-k}b^k$(Eqn 11)
with binomial coefficients
$\displaystyle ~^n\!C_r = \dfrac{n!}{r!(n-r)!}$(Eqn 15)
where factorial n is defined by n! = 1 × 2 × 3 ... (n − 1) × n and 0! = 1.
- 3
-
Useful properties of the binomial coefficient include
nCn = 1(Eqn 16)
nC0 = 1(Eqn 17)
nCn−r = nCr(Eqn 18)
nCr = n−1Cr + n−1Cr−1(Eqn 19)
- 4
-
Useful Section 3infinite series include
$\displaystyle \exp(x) = \sum_{n=0}^{\infty} \dfrac{x^n}{n!} = 1 + \dfrac{1}{1!} + \dfrac{1}{2!} + \dfrac{1}{3!} + \dots~~\text{for all}~x$(Eqn 22)
$\displaystyle \sin(x) = \sum_{n=0}^{\infty} \dfrac{(-1)^nx^{2n+1}}{(2n+1)!} = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \dots~~\text{for all}~x$(Eqn 23)
$\displaystyle \cos(x) = \sum_{n=0}^{\infty} \dfrac{(-1)^nx^{2n}}{(2n)!} = x - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \dots~~\text{for all}~x$(Eqn 24)
$\displaystyle \loge(1-x) = \sum_{n=1}^{\infty} \dfrac{x^n}{n} = -x \dfrac{x^2}{2} - \dfrac{x^3}{3} - \dfrac{x^4}{4} - \dots~~\text{for}~-1 \le x \lt 1$(Eqn 25)
The Subsection 2.7binomial series
$\displaystyle (1+x)^r = 1 + \dfrac{rx}{1!} + \dfrac{r(r-1)x^2}{2!} + \dfrac{r(r-1)(r-2)x^3}{3!} + \dots~~\text{for}~-1 \lt x \lt 1$(Eqn 26)
- 5$\vphantom{\displaystyle \sum_{n=1}^{\infty}}$
-
If the series $\displaystyle \sum_{n=1}^{\infty} a_n$ converges then $\displaystyle \lim_{n\rightarrow\infty}(a_n)=0$, though the converse is not necessarily true.
- 6
-
D’Alembert’s ratio test is one of many tests that can be used to investigate convergence. To apply this test to a sum of positive terms $\displaystyle \sum_{n=1}^N a_n$, we write $\displaystyle \lim_{n\rightarrow\infty}\left(\dfrac{a_{n+1}}{a_n}\right)$, there are then three possible outcomes:
if R < 1 the series is convergent,
if R > 1 the series is divergent, and
if R = 1 the test fails. - 7
-
The correctness of formulae for the sums of series can sometimes be established by the method of induction. To apply this method first show that if a result is true for some value of a parameter, such as n, then it is also true for (n + 1). Then complete the proof by showing that the result is true for the smallest allowable value of n.
- 8
-
Useful approximations obtained by truncating infinite series include:
$\sin(x) \approx x - \dfrac{x^3}{3!} \quad\cos(x) \approx 1 - \dfrac{x^2}{2!}$ and (1 + x) r ≈ 1 + rx for | x | < 1
4.2 Achievements
Having completed this module, you should be able to:
- A1
-
Define the terms that are emboldened and flagged in the margins of the module.
- A2
-
Define a sequence and describe how a sequence may be used to define a series.
- A3
-
Describe how the summation symbol, ∑, may be used to define series.
- A4
-
Use rules for manipulating the summation symbol.
- A5
-
Use formulae for the summation of powers of the positive integers.
- A6
-
Define the arithmetic progression, geometric progression and binomial series and use formulae for their sums.
- A7
-
Define the factorial and the binomial coefficient and recall useful identities for them.
- A8
-
Use the method of induction to verify appropriate formulae.
- A9
-
Recall series for some of the elementary functions, such as exp(x), sin(x), cos(x), loge(1 − x) and (1 − x) r.
- A10
-
Explain what is meant by convergent and divergent series.
- A11
-
Apply the d’Alembert’s ratio test for convergence of an infinite series.
- A12
-
Use series to provide approximations to functions and numerical constants.
Study comment You may now wish to take the following Exit test for this module which tests these Achievements. If you prefer to study the module further before taking this test then return to the topModule contents to review some of the topics.
4.3 Exit test
Study comment Having completed this module, you should be able to answer the following questions, each of which tests one or more of the Achievements.
Question E1 (A2)
Define what is meant by the terms sequence, finite series, infinite series and sum of an infinite series.
Answer E1
A sequence is an ordered collection of numbers.
A finite series is the sum of a finite sequence of numbers, that is $\displaystyle \sum_{i=n}^m a_i$ where both m and n are finite.
Loosely speaking, an infinite series is the sum of an infinite sequence of numbers and is written in the form $\displaystyle \sum_{i=n}^{\infty} a_i$. However, since it is impossible to perform an infinite summation, it is more accurately described as a sequence of sums of the form $\displaystyle \sum_{i=1}^{N} a_i$, where the upper limit, N, may be as large as we please.
The definition may also be extended to series of the form $\displaystyle \sum_{i=-\infty}^{\infty} a_i$ and $\displaystyle \sum_{i=k}^{\infty} a_i$. The sum of an infinite series $\displaystyle \sum_{i=1}^{\infty} a_i$ is the limit of the sums $\displaystyle \sum_{i=1}^{N} a_i$, as N becomes large, if this limit exists.
(Reread Subsections 2.1, 2.2 and 3.1 if you had any difficulty with this question.)
Question E2 (A2 and A3)
Given a sequence of n numbers, xi, and a constant, c, what is $\langle y \rangle$ (the mean of yi) in terms of $\langle x \rangle$ (the mean of xi) in the following cases:
(a) yi = xi + c, (b) yi = c xi
Answer E2
(a) $\displaystyle \langle y \rangle = \dfrac 1N\sum_{i=1}^N y_i = \dfrac 1N\sum_{i=1}^N x_i + \dfrac 1N\sum_{i=1}^N c = \langle x \rangle + c$
(b) $\displaystyle \langle y \rangle = \dfrac1N\sum_{i=1}^N y_i = \dfrac 1N\sum_{i=1}^N cx_i = c\langle x \rangle$
(Reread Subsection 2.2 if you had any difficulty with this question.)
Question E3 (A2, A5 and A6)
Identify which of the following series are examples of a binomial series, geometric progression or arithmetic progression. In each case, use the appropriate formula to work out the sum of the series. i
(a) 3 + 7 + 11 + 15 + 19, (b) 3 + 12 + 48 + 192 + 768, (c) x4 + 4x3y+ 6x2y2 + 4xy3 + y4
Answer E3
(a) The difference between each successive term is 4 so this is an arithmetic progression. Such series have the general form
$\displaystyle \sum_{k=0}^{n-1} (a + kh) = a + (a + h) + (a + 2h) + \dots + [a + (n - 1)h]$
In this case, the common difference, h, is equal to 4 and a is 3. Since there are five terms, we also have n = 5.
The sum of an arithmetic progression is given by
$\dfrac n2[2a + (n - 1)h]$
so in this case we find
$\dfrac n2[2a + (n - 1)h] = 25 [2 \times 3 + (5 - 1) \times 4] = 55$
(b) Each term in this series is 4 times the previous term, so this is a geometric progression. Such series have the general form
$\displaystyle \sum_{k=1}^{n} (ar^{k-1}) = a + ar + ar^2 + \dots + ar^{n - 1}$
In this case, the common ratio, r, is equal to 4 and a is 3. Since there are five terms, we have n = 5.
The sum of a geometric progression is given by
$\dfrac{ a(r^n-1)}{(r - 1)}$
and in this case we have
$\dfrac{ a(r^n-1)}{(r - 1)} = \dfrac{3(4^5-1)}{(4-1)}=1023$
(c) This looks as if it might be a binomial expansion since the coefficients are symmetric and the sum of the powers of x and y is always 4. To verify this we note that such series have the general form
$\begin{align}(a+b)^n & = ~^n\!C_na^n + ~^n\!C_{n-1}a^{n-1}b + \dots + ~^n\!C_{n-r}a^{n-r}b^r + \dots + ~^n\!C_1ab^{n-1} + ~^n\!C_0b^n\\ & = \sum_{k=0}^{n} ~^n\!C_{n-k}a^{n-k}b^k\\ \text{where} \quad^n\!C_r & =\dfrac{n(n-1)(n-2)\dots(n-r+2)(n-r+1)}{r(r-1)(r-2)\dots2\times 1}\end{align}$
In this particular case we have five terms, so n = 4, a = x and b = y. Substituting these values in the general expression for the binomial series, we find
$\begin{align}(x+y)^4 & = ~^4\!C_4x^4 +~^4\!C_3a^3y +~^4\!C_2x^2y^2 +~^4\!C_1xy^3 +~^4\!C_0y^4\\ & = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4\end{align}$
which is the series given in the question. In general, the sum of a binomial series is (a + b) n. In this case the sum is (x + y)4.
(Reread Subsections 2.5, 2.6 and 2.7 if you had any difficulty with this question.)
Question E4 (A3 and A4)
Use the formulae for summing powers of the positive integers, given in Subsection 2.4, to show that
$\displaystyle \sum_{k=1}^n k(n^2-k^2) = \dfrac{n^2(n^2-1)}{4}$
Answer E4
Since n is a constant, independent of k, we have
$\begin{align} \sum_{k=1}^n k(n^2-k^2) & = n^2 \sum_{k=1}^n k - \sum_{k=1}^n k^3\\ & = n^2\dfrac{n(n+1)}{2} - \dfrac{n^2(n+1)^2}{4}\\& = \dfrac{n^2(n+1)}{4}[2n-(n+1)] = \dfrac{n^2(n+1)(n-1)}{4}\\& =\dfrac{n^2(n^2-1)}{4}\end{align}$
(Reread Subsection 2.4 if you had any difficulty with this question.)
Question E5 (A4 and A6)
Show that, for n > 0,
$\displaystyle \sum_{k=0}^n (-1)^k ~^n\!C_k = 0$
[Hint: Consider the binomial expansion of (1 − 1) n with n an integer greater than zero.]
Answer E5
Using the binomial expansion (Equation 11),
$\displaystyle (a+b)^n = \sum_{k=0}^n ~^n\!C_{n-k}a^{n-k}b^k$(Eqn 11)
we have
$\displaystyle (1-1)^n = \sum_{k=0}^n ~^n\!C_{n-k}(1)^{n-k}(-1)^k$
but$(1)^{n-k} = 1$
and$^n\!C_{n-k} = ~^n\!C_k$(Eqn 18)
So, $\displaystyle (1-1)^n = \sum_{k=0}^n ~^n\!C_k(-1)^k$
but$(1 - 1)^n = 0^n = 0$
So,$\displaystyle 0 = \sum_{k=0}^n ~^n\!C_k(-1)^k$
(Reread Subsection 2.7 if you had any difficulty with this question.)
Question E6 (A8)
Use the method of induction to show that
$\displaystyle \sum_{k=1}^n (2k-1) = n^2$
Answer E6
Consider the expression
$\displaystyle \sum_{k=1}^{n+1} (2k-1) = \sum_{k=1}^{n} (2k-1) + \sum_{k=n+1}^{n+1} (2k-1) = \sum_{k=1}^{n} (2k-1) + [2(n+1)-1]$
Using the result given in the question, this can be rewritten as
n2 + [2 (n + 1) − 1] = (n + 1)2
So if the result is true for n, it is true for n + 1.
But for the lowest allowed value of n (that is, n = 1), the result is also true, since
$\displaystyle \sum_{k=1}^1 (2k-1) = 1$
andn2 = 12 = 1
Therefore the result is proved by induction.
(Reread Subsection 2.6 if you had any difficulty with this question.)
Question E7 (A9)
The following expression for the interaction energy U occurs in the study of an ionic crystal (such as sodium chloride)
$U = -\dfrac{2q^2}{a}\left(1 - \dfrac12 + \dfrac13 - \dfrac14 + \dfrac15 - \dfrac16 + \dots \right)$
where q and a are constants. Use the series given in Subsection 3.1 to write this expression in terms of a well known function (or functions).
Answer E7
Apart from an overall factor, the series is
$\displaystyle \sum_{n=1}^{\infty} \dfrac{(-1)^n}n$
which has the two features: an alternating sign and a factor of 1/n. Looking at the series given in Subsection 3.1, we see that the logarithmic function
$\displaystyle \loge(1-x) = - \sum_{n=1}^{\infty} \dfrac{x^n}n = -x -\dfrac{x^2}2-\dfrac{x^3}3-\dfrac{x^4}4-\dots$ for −1 ≤ x < 1 is a likely candidate.
In fact, setting x equal to −1, we find
$\displaystyle \loge(1 + 1) = - \sum_{n=1}^\infty \dfrac{(-1)^n}n = 1 -\dfrac12+\dfrac13-\dfrac14+\dots$
and therefore we can write
$U = -\dfrac{2q^2}{a}\loge(2)$
(Reread Subsection 3.1 if you had any difficulty with this question.)
Question E8 (A9 and A12)
Use the series for exp(x) as powers of x to find the number e (that is, exp(1)) to two decimal places.
Check that the result is consistent with that given by your calculator.
Use a series to approximate exp(1/2) and then use your calculator to verify that $\exp(1/2) \approx \sqrt{\exp(1)}$.
Answer E8
The series for exp(x) is
$\displaystyle \exp(x) = \sum_{n=0}^{\infty} \dfrac{x^n}{n!} = 1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dots$ for all x
and therefore
$\begin{align} e & = \exp(1) = \sum_{n=0}^{\infty} \dfrac{1}{n!}\\& = 1+\dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!}+\dfrac{1}{5!}+\dots\\ & \approx 1 + 1 + 0.5 + 0.166\,67 + 0.041\,67 + 0.008\,33 + \dots\end{align}$
All other terms are smaller than 0.008133 and can be neglected. (This is not a rigorous argument.)
Summing the terms shown we find
e ≈ 2.72
which is consistent with the result of 2.718 282 given by a calculator.
$\begin{align} \exp\left(\dfrac12\right) & = \sum_{n=0}^{\infty} \dfrac{1/2^n}{n!}\\& = 1 + \dfrac{1}{2\times 1!} + \dfrac{1}{4\times 2!} + \dfrac{1}{8\times 3!} + \dfrac{1}{16\times 4!} + \dots\\& \approx 1 + 0.5 + 0.125 + 0.020\,83 + 0.002\,604 + \dots\\& \approx 1.65\end{align}$
and my calculator gives $\sqrt{e\os} \approx 1.648\,721$.
(Reread Subsection 3.1 if you had any difficulty with this question.)
Question E9 (A10 and A11)
Use d’Alembert’s ratio test to examine the convergence of the series $\displaystyle \sum_{n=0}^{\infty} \dfrac{n!}{2^n}$.
Answer E9
The nth term in the series is given by
$\begin{align} a_n & = \dfrac{n!}{2^n}\\\text{so}~~~~R & = \lim_{n\rightarrow\infty} \left(\dfrac{a_{n+1}}{a_n}\right) = \lim_{n\rightarrow\infty}\left(\dfrac{(n+1)!}{2^{n+1}}\dfrac{2^n}{n!}\right)\\ & = \lim_{n\rightarrow\infty} \dfrac{n+1}{2} = \infty\end{align}$
Since R is greater than 1, d’Alembert’s ratio test implies that the series diverges.
(Reread Subsection 3.3 if you had any difficulty with this question.)
Study comment This is the final Exit test question. When you have completed the Exit test go back and try the Subsection 1.2Fast track questions if you have not already done so.
If you have completed both the Fast track questions and the Exit test, then you have finished the module and may leave it here.
Study comment Having seen the Fast track questions you may feel that it would be wiser to follow the normal route through the module and to proceed directly to the following Ready to study? Subsection.
Alternatively, you may still be sufficiently comfortable with the material covered by the module to proceed directly to the Section 4Closing items.